基于断裂力学的TBM撑靴液压缸O形圈断裂分析

李　琳　张峰榕　陶建峰　刘成良

上海交通大学，上海，200240



基于断裂力学的TBM撑靴液压缸O形圈断裂分析

李琳张峰榕陶建峰刘成良

上海交通大学，上海，200240

摘要：为研究全断面岩石隧道掘进机(TBM)的撑靴液压缸中O形圈的断裂原因，采用断裂力学分析了不同泊松比和初始裂纹情况下，O形圈可承受的最大应力，并采用ANSYS仿真分析了在某型号TBM实际工作情况下的O形圈的受力情况。结果表明,在TBM工作过程中，由于工作条件的复杂，O形圈的局部应力会超出裂纹迅速扩展时能够承受的最大应力，进而使O形圈断裂。根据理论分析和仿真结果得出，为了避免O形圈断裂，TBM撑靴液压缸的O形圈应严格控制微裂纹并选择较大泊松比。

关键词：全断面岩石隧道掘进机；断裂力学；O形圈；有限元仿真

0引言

与传统的爆破施工相比，由全断面岩石隧道掘进机(full face hard rock tunnel boring machine， TBM)修建的隧道具有高效、安全、岩壁质量好等特点，是目前长大隧道施工的重要方法，广泛应用于铁路、公路、水电工程和城市地铁等重大工程[1]。撑靴液压缸为TBM的掘进提供支撑力，若其出现故障，TBM将无法工作。经调研，撑靴液压缸易出现密封件断裂、活塞杆划伤、缸体点蚀等损伤，造成液压油泄漏、支撑力不足等故障，导致TBM停机，造成巨大的时间和资金的损失。因此，对撑靴液压缸的损伤机理进行分析有重要的研究意义。

液压缸具有结构简单、工作可靠、传递功率大等特点，常用于工程机械中，液压缸的密封件可以防止工作介质的泄漏以及外界污染物的侵入，其密封性能和损伤的研究受到了极大关注。Nikas等[2]研究了不同温度和压力下密封件的性能。董作见等[3]采用断裂力学分析了O形圈的疲劳寿命，并结合实验和仿真说明了基于断裂力学计算O形圈疲劳寿命的合理性。随着有限元仿真软件的发展，部分研究人员采用ANSYS分析了O形圈的工作应力情况，通过仿真可直观地发现在压力作用下，液压缸密封件所受的von Mises应力分布不均匀，有明显的应力集中现象[4-5]。在研究O形圈的文献中，主要采用仿真的方法关注局部应力或疲劳寿命，而O形圈在实际工作中的断裂原因分析较少，影响O形圈断裂的因素不确定，难以为预防O形圈损伤提供理论依据，且无法确定设计使用中应注意的问题。断裂力学是研究含裂纹物体的强度和裂纹扩展过程的学科，采用断裂力学可以有效地解释构件低应力脆断的原因。Perl等[6]使用断裂力学分析了球形压力容器中的径向和环向裂纹尖端的三维应力强度因子，并说明了高压容器中裂纹扩展的影响因素。

本文基于断裂力学计算了TBM撑靴液压缸O形圈在有隐含裂纹的情况下能够承受的最大应力，分析了泊松比和初始裂纹长度对O形圈断裂的影响，采用ANSYS仿真说明了最终断裂的原因，并提出了O形圈在使用中的注意事项。

1TBM撑靴液压缸受力分析

TBM撑靴系统由撑靴液压缸、左右撑靴和连接件组成，其结构如图1所示。其中，撑靴液压缸的无杆腔连为一个整体，有杆腔相互分离，分别支撑左右撑靴；撑靴液压缸通过十字销轴与鞍架连接，并通过左右各两个竖向扭矩液压缸将撑靴液压缸悬挂在鞍架上。十字销轴与鞍架用螺栓连接，且鞍架内前后左右共装有4个带弹簧的顶块，分别顶住左右撑靴液压缸的前后侧，以避免其过于摇摆。这种十字销轴“浮动撑靴系统”的设计结构，允许撑靴液压缸前后、上下、左右有一定幅度的摆动和倾斜，以适应TBM姿态的变化和洞室开挖产生的误差[1]。

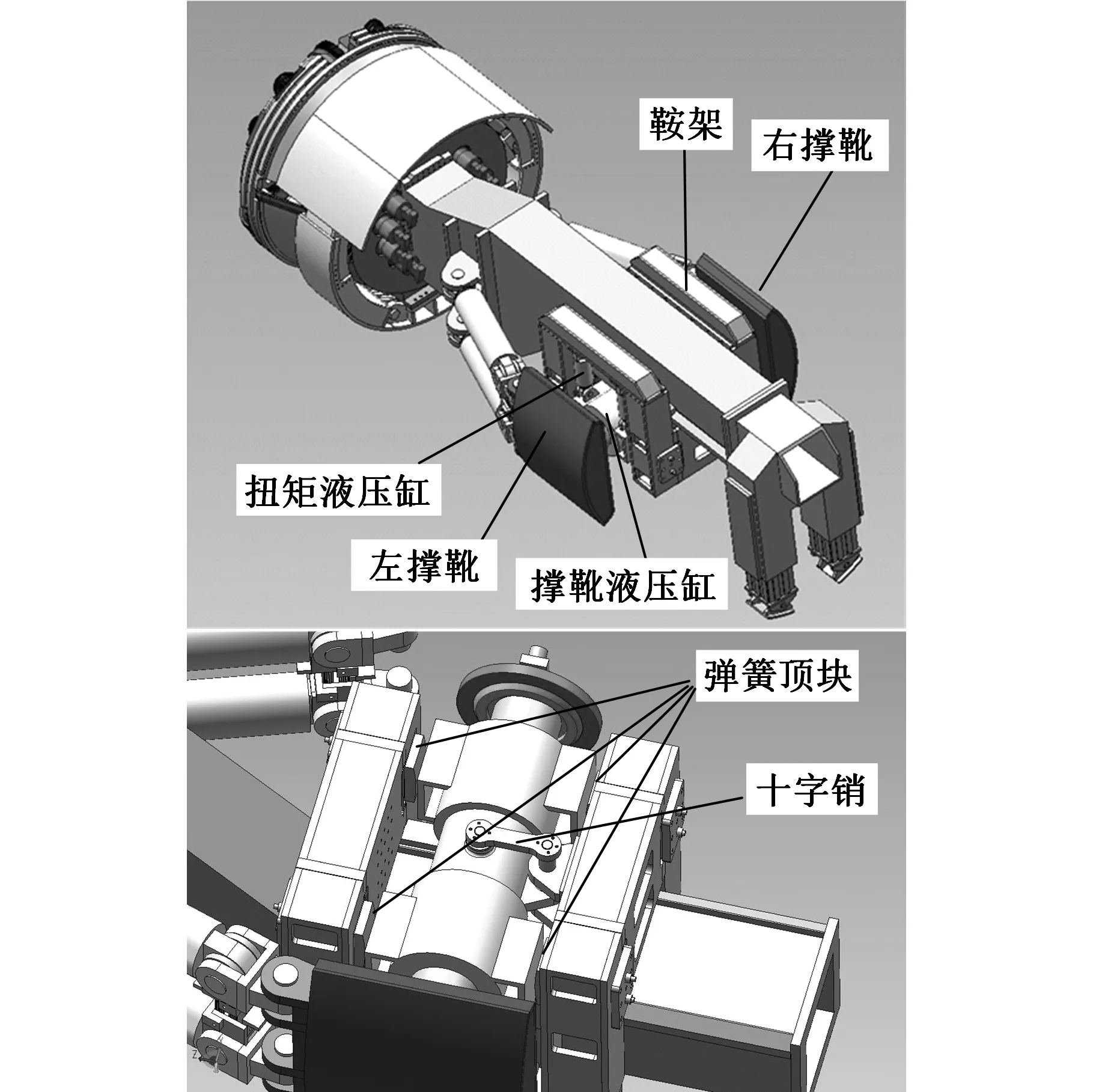
图1　TBM撑靴系统图

为了分析O形圈断裂的原因，首先应明确撑靴液压缸的受力情况。将撑靴液压缸作为分析对象，其与鞍架连接的十字销之间的作用力视为内力，不考虑其对撑靴液压缸的影响；TBM在掘进过程中，撑靴液压缸的活塞杆径向作用于岩壁上承受压力和扭矩，为了给TBM提供足够的支撑力，撑靴液压缸工作于高压状态，高压油通过换向阀进入液压缸大腔，并通过单向阀和平衡阀保压，使其持续工作于高压状态[7]，缸体内部受到高压油压力，为35 MPa；此外，扭矩液压缸提供一个与撑靴液压缸成一定角度的拉紧力，在TBM工作过程中，通过调节扭矩油缸的拉紧力可实现TBM的方向微调，考虑极限情况，将拉紧力正交分解为水平方向拉力3 kN和竖直方向拉力7 kN；岩壁提供与撑靴液压缸撑紧压力相应的支反力，限制了撑靴液压缸所有方向的自由度。综上，将撑靴液压缸的受力简化为重力、液压油压力和扭矩油缸的拉紧力，其受力如图2所示。

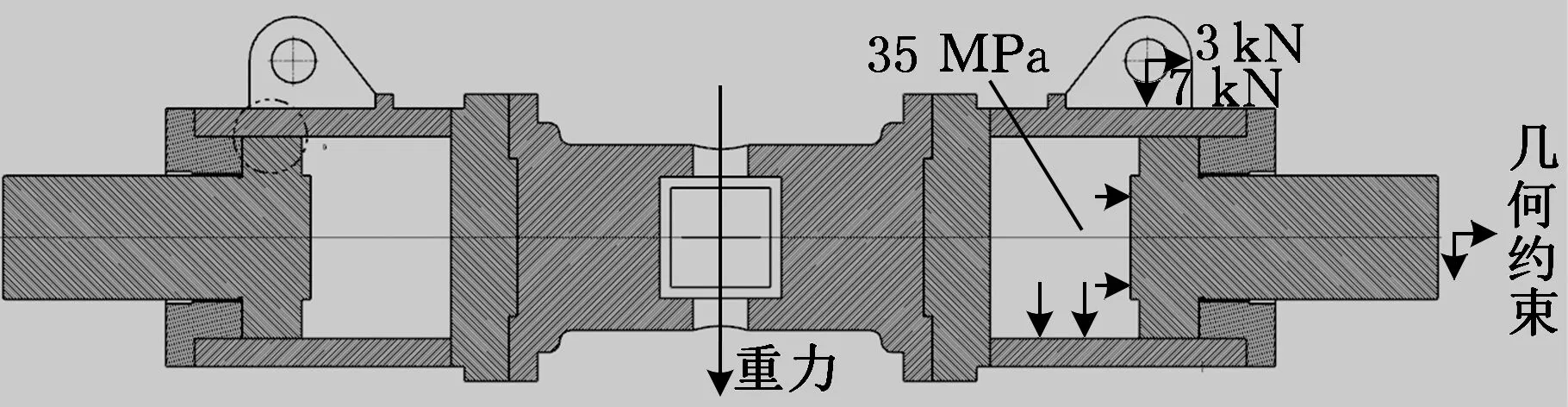
图2　TBM撑靴液压缸受力简图

撑靴液压缸的结构复杂，难以通过简单的受力分析求解撑靴液压缸的应力分布，故采用有限元法仿真求解撑靴液压缸的应力情况。首先，根据某一型号TBM的撑靴液压缸的尺寸，采用UG软件建立了撑靴液压缸的实体模型，作为有限元分析的几何模型，其3D效果如图3所示。

图3　TBM撑靴液压缸3D图

液压缸的活塞和缸体之间具有接触性质，接触问题是典型的高度非线性行为[8]，计算量巨大，根据撑靴油缸的几何对称性，为降低计算量，取1/2模型进行分析。接触非线性主要来源于两个方面：①接触界面区域大小和相互位置以及接触状态均是未知的，且随时间变化，需要在求解过程中确定；②接触条件是非线性的，接触物体不可相互侵入、接触力的法向分量只能是压力、切向接触的摩擦条件，这些条件都区别于一般的约束条件，是单边性的不等式，有强烈的非线性。ANSYS用接触单元来模拟接触问题，可跟踪接触位置，保证接触的协调性，在接触表面之间传递接触应力。其中，面-面接触单元主要用于任意形状的两个表面之间的接触[9]。使用面-面接触单元时，不必预先知道确切的接触位置，接触面之间不需要保持一致的网格，且支持大的相对滑动、大应变和大转动，允许有大的变形。面-面接触单元适用于复杂表面、大变形、含摩擦力的动静态接触问题的求解。本文采用面-面接触单元模拟液压缸缸体和活塞杆之间的接触特性。

在有限元分析中，应首先定义各个部件的材料参数和单元类型，液压缸缸体和活塞杆材料均为45钢，其密度为7800 kg/m3，屈服强度为500 MPa；为了近似模拟液压缸缸体和活塞杆的实际情况，选择Solid 185单元模拟实体。根据图2的受力分析，对液压缸施加约束条件和载荷，检查后进行求解。

ANSYS具有强大的求解功能，但是网格划分能力较弱，由于撑靴液压缸的结构复杂，ANSYS对其网格划分难以控制，精度不足，因此，采用HyperMesh进行网格划分，网格划分结果如图4所示。在HyperMesh中设置边界条件、接触模型和受力情况，生成cdb模型后，导入ANSYS进行分析求解。ANSYS求解的结果如表1所示。

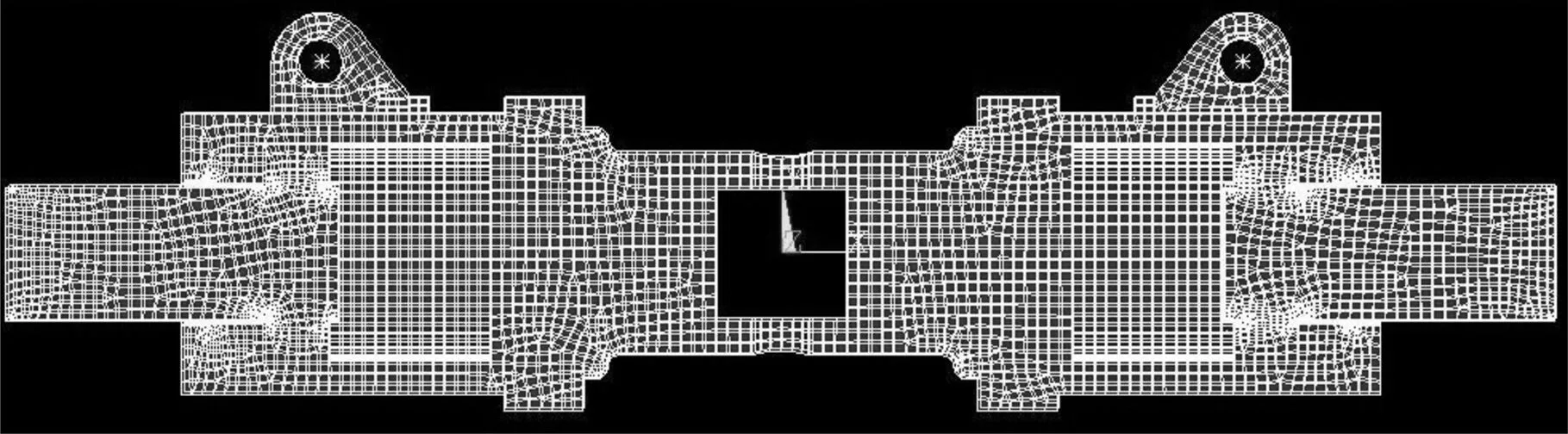
图4　TBM撑靴液压缸网格划分结果

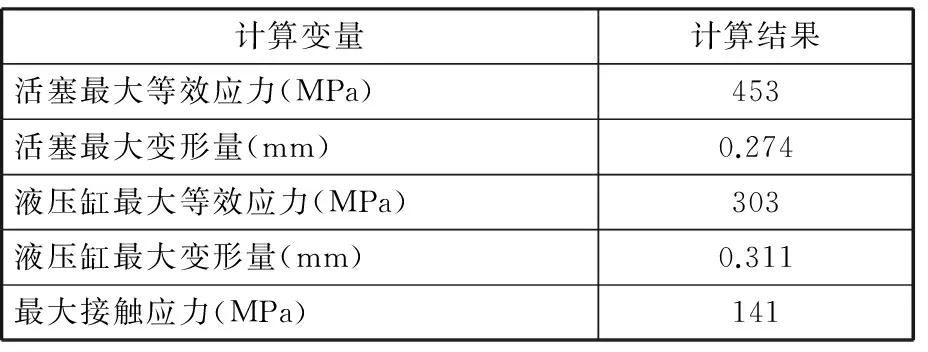
表1　有限元分析结果

根据表1的结果，撑靴液压缸在TBM正常工作的情况下，缸体和活塞缸的最大等效应力均未超过45钢的屈服应力，可以保证撑靴液压缸的正常工作。但是，液压缸的O形圈出现了断裂的情况，因此，需要单独分析O形圈局部受力情况。

无论是传统汉学阶段，还是新汉学阶段，长期以来，国内学界对海外中国研究成果翻译较多，系统梳理后的引进介绍并不多；批判较多，对其概念、理论与方法的借鉴与反思并不多。这正是受其研究视角的影响，毕竟多数学者对海外新汉学尤其是其中的政治研究表示质疑，而持审慎肯定态度的建构视角的学者并不多见。

2O形圈的断裂分析

固体的断裂几乎总是由于物体中出现某些位移间断面而引起的，一般将裂纹划分为3种基本类型：Ⅰ为张开型，其裂纹表面位移彼此相反，方向均垂直于裂纹方向，工程上最为常见；Ⅱ为滑开型，裂纹上下表面位移彼此相反；Ⅲ为撕开型，裂纹上下表面产生方向相反的离面位移[10-11]。液压缸的O形圈的主要断裂形式可近似看作Ⅰ型裂纹，因此，采用I型裂纹的分析方法进行分析。

应力强度因子的临界值KIC称为材料的断裂韧度，是常用的判定断裂的方法，下标表示Ⅰ型裂纹。裂纹长度a、材料断裂韧度KIC与裂纹端点正前方能够使裂纹面张开的拉伸应力σf之间的关系可表示为[11]

(1)

其中，α为几何参数，常取α=1。

对于延性材料，在断裂的过程中所释放的能量主要耗散在裂纹尖端附近材料的塑性流动中，满足这些能量耗散的应变能释放率被称为临界应变能释放率，用GC表示。对于Ⅰ型裂纹，可得

(2)

式中，E为弹性模量。

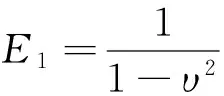
(3)

式中，υ为泊松比。

根据断裂强度因子和应变能释放率的关系，可得研究断裂极限应力与应变能释放率GCr的关系，即

(4)

TBM撑靴液压缸的O形圈的材料为橡胶，取橡胶的弹性模量E=1.4GPa，橡胶应变能释放率G=13kN/m，模拟O形圈在初始裂纹为1mm的条件下，泊松比υ变化时裂纹尖端能够承受的最大应力，结果如图5所示，随着泊松比的增大，O形圈能够承受的极限应力增大。

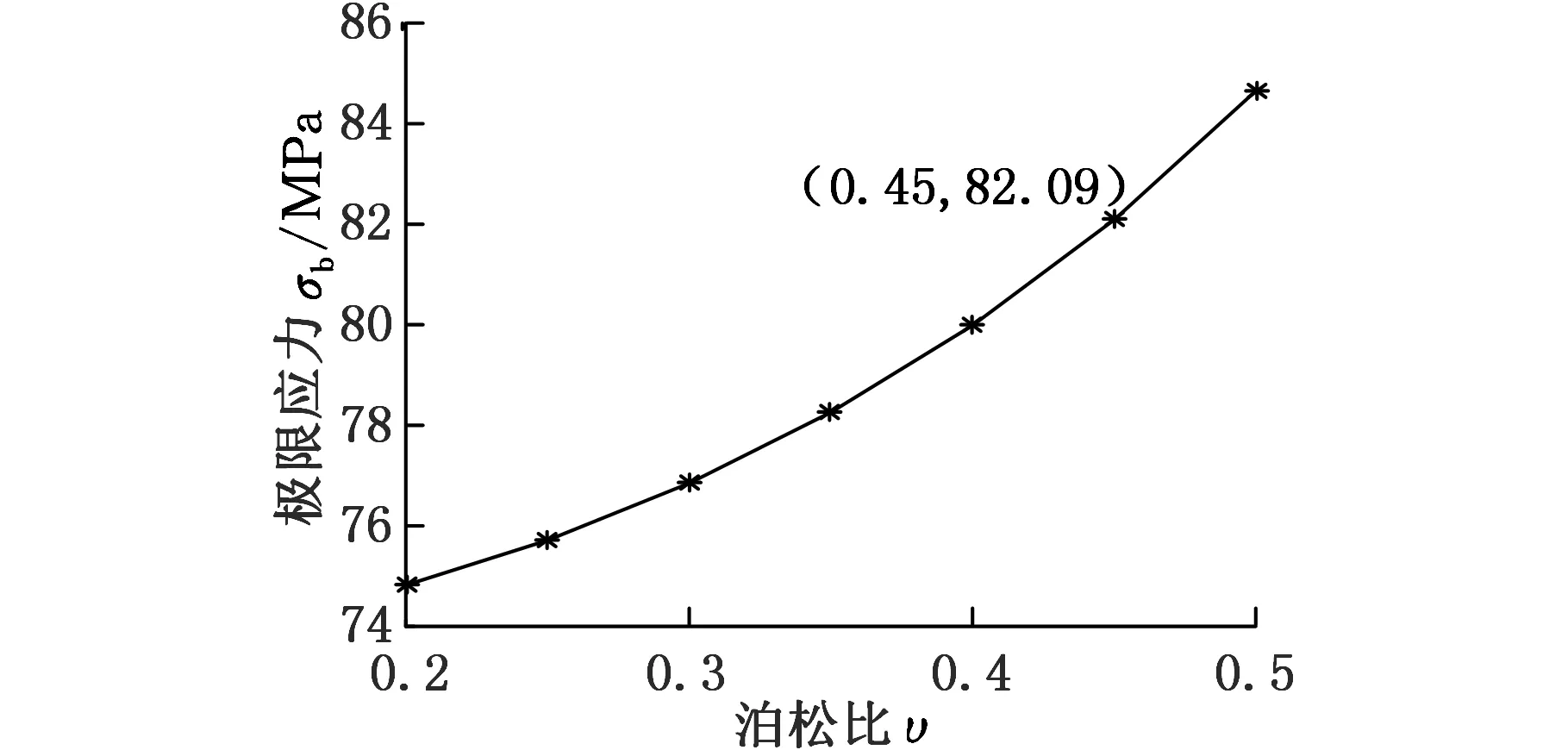
图5　不同泊松比下O形圈可承受的最大应力

此外，模拟在泊松比υ=0.45时，在不同初始裂纹的情况下，裂纹尖端能够承受的最大应力，结果如图6所示，随着裂纹长度的增大，O形圈能够承受的极限应力减小。

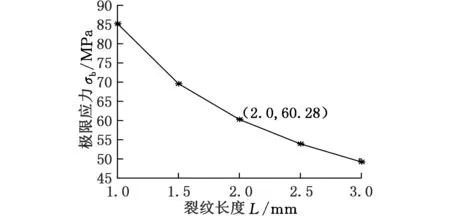
图6　不同裂纹长度下O形圈可承受的最大应力

3TBM撑靴液压缸O形圈的有限元分析

第2节基于断裂力学从理论上分析了不同泊松比和初始裂纹的O形圈在裂纹不迅速扩展的情况下能够承受的最大应力，现采用ANSYS仿真分析O形圈的受力情况，并分析其断裂的原因。由于撑靴液压缸对密封的特殊要求，O形圈不与缸筒直接接触，而是与聚四氟乙烯的隔圈接触，和直接与结构钢接触的O形圈相比，聚四氟乙烯的弹性模量较小，易于变形，且摩擦因数较小，增大了材料的非线性，使计算更加难于收敛。

橡胶材料具有高弹性，为了正确仿真O形圈的材料非线性，采用Mooney-Rivlin橡胶模型[12]，Mooney模型是基于以下假设得出的：①橡胶材料是各向同性的；②橡胶材料的体积变化不考虑，即体积不可压缩或近似不可压缩；③不考虑迟滞作用。Rivlin认为性质为各向同性且不可压缩或近似不可压缩的橡胶材料的应变能函数必然可以由3个应变不变量I1、I2、I3所组成的函数进行表示，应变不变量I1、I2、I3可表示为

(5)

其中，λ1、λ2、λ3为各边的伸长率，J为初始位置和最终位置的体积比，由假设中橡胶材料的体积不变性可知，体积比近似为1∶1，则取J=1，所以式(5)可以简化为

(6)

当材料不可压缩时，第三个不变量应为零，Rivlin推导出了不可压缩材料的应变能密度函数模型，此时橡胶类非线性材料的应变能函数可表示为

(7)

在ANSYS程序中，可用Mooney-Rivlin模型来表征不可压缩橡胶类材料的超弹性特性，本文采用2个材料参数的Mooney-Rivlin模型，其应变能函数为

W=C10(I1-3)+C01(I2-3)

(8)

其中，C10、C01为材料常数。C10、C01是通过实验获得的，在仿真中C10和C01值分别为2.5MPa和1.1MPa。

此外，油温对橡胶的性能有明显影响[13]，为了能够快速求解，简化计算，作出如下假设：

(1)橡胶密封圈材料具有确定的弹性模量和泊松比，取弹性模量E=1.4GPa，泊松比υ=0.45；

(2)橡胶材料是均匀连续的；

(3)挡圈的弹性模量远大于密封圈的弹性模量，挡圈作为刚体进行分析，并且其结构在理想情况下是完全轴对称的；

(4)密封圈受到的纵向压缩是由约束边界的指定位移引起的；

(5)忽略油液温度的变化对密封圈密封性能的影响，假定油液温度不变。

根据以上假设，首先计算O形圈的变形量ω作为约束的位移：

(9)

式中，d0为O形密封圈在自由状态下的截面直径；h为O形密封圈压缩后的截面高度。

基于某型号TBM撑靴液压缸的O形圈尺寸，建立有限元模型，根据Mooney-Rivlin橡胶模型，设置O形圈的材料参数，并进行网格划分；网格划分完成后，需对O形圈施加约束，其中，X轴方向为UX=0；Y轴负方向约束可按式(9)计算，求出UY=-0.002 35m；在挡圈上施加全约束，其他边界无约束。

通过非线性求解可得O形圈的vonMises等效应力情况。vonMises应力是基于剪切应变能的一种等效应力，其等效表达式为

(10)

式中，σ1、σ2、σ3为单元体三个方向的主应力。

vonMises应力综合考虑了第一、第二、第三主应力，可以用来对破损失效、疲劳失效等进行评价。vonMises应力的大小反映的是密封圈截面上主应力差值的大小。一般情况下，vonMises应力值越大的区域，在此区域材料越容易出现疲劳破坏产生裂纹，密封圈越容易发生破损，从而破坏失效。采用ANSYS仿真分析得到的结果如图7和图8所示。

由图7可得，由于局部接触作用，O形圈的最大vonMises应力为32.8MPa，分布最广泛的vonMises应力为7.28MPa；由图8可得，最大接触应力为82.9MPa，分布最广的接触应力为36.8MPa。

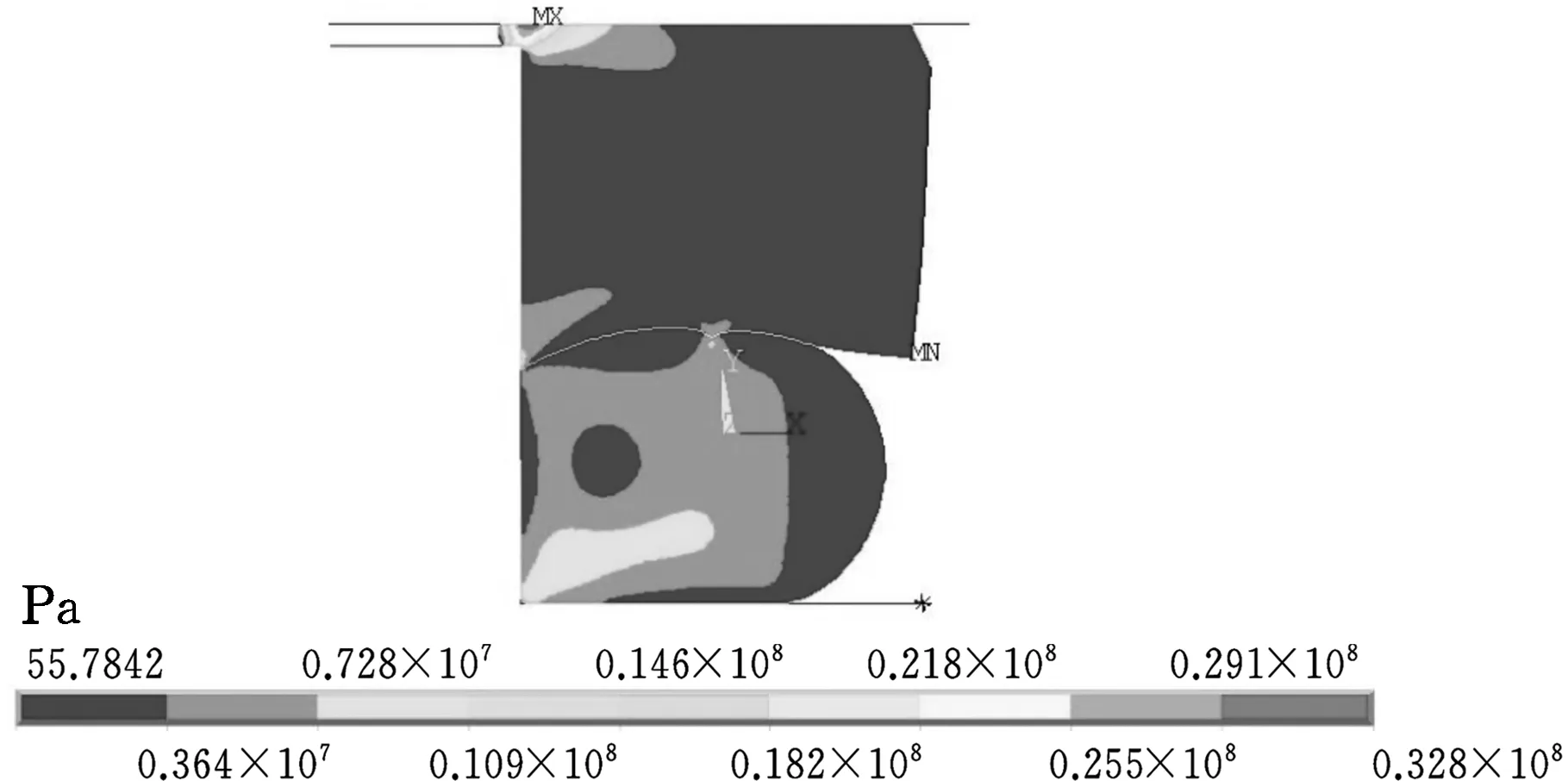
图7　O形圈的von Mises应力

图8　O形圈的接触应力

根据第2节断裂力学分析可知，在O形圈泊松比为0.45，且有1mm左右的裂纹时，O形圈可以受的最大应力为82.22MPa左右，根据有限元仿真的结果可知，在TBM工作过程中，振动强烈，会出现应力集中现象，O形圈局部应力集中的位置最大接触应力为82.9MPa，超过了O形圈可承受的应力，使裂纹迅速扩展，进而使O形圈断裂。

4结论

基于断裂力学的理论分析，可以得到如下结论：随着橡胶泊松比的增加，O形圈所能承受的极限应力增大；随着初始裂纹长度的增加，O形圈所能承受的极限应力减小。通过ANSYS仿真可知，TBM的撑靴液压缸工作于高压状态的情况下，O形圈局部承受的应力超过了其具有隐含裂纹时的极限应力，即如果O形圈内部含有隐含裂纹，在TBM工作工程中，裂纹会迅速扩展直至断裂。因此，在使用过程中，应及时检查O形圈的内部结构，确保其不存在隐含微裂纹。同时应选用泊松比较大的O形圈，从而减少TBM的O形圈断裂情况，保证其正常工作。

参考文献：

[1]杜彦良，杜立杰，等.全断面岩石隧道掘进机——系统原理与集成设计[M]. 武汉：华中科技大学出版社， 2011.

[2]Nikas G K, Almond R V, Burridge G. Experimental Study of Leakage and Friction of Rectangular, Elastomeric Hydraulic Seals for Reciprocating Motion from -54 to+135℃ and Pressures from 3.4 to 34.5 MPa[J]. Tribology Transactions, 2014， 57(5): 846-865.

[3]董作见,吴晓,王忠，等.基于断裂力学的O型密封圈疲劳性能研究[J]. 润滑与密封，2014，39(11)：59-62.

Dong Zuojian, Wu Xiao, Wang Zhong，et al. Research on Fatigue Performance of O-ring Based on Fracture Mechanics[J]. Lubrication Engineering. 2014,39(11):59-62.

[4]徐同江.基于ANSYS的O形密封圈的有限元分析[D].济南：山东大学，2012.

[5]关文锦，杜群贵，刘丕群.橡胶O形圈密封性能的有限元分析[J].润滑与密封， 2012， 37(6)：60-64.Guan Wenjin, Du Qungui, Liu Piqun. Finite Element Analysis of the Sealing Performance of Rubber O-ring[J]. Lubrication Engineering, 2012, 37(6): 60-64.

[6]Perl M，Steiner M. 3-D Stress Intensity Factors Due to Full Autofrettage for Inner Radial or Coplanar Crack Arrays and Ring Cracks in a Spherical Pressure Vessel[J]. Engineering Fracture Mechanics, 2015, 138: 233-249.

[7]周赛群.全断面硬岩掘进机(TBM)驱动系统的研究[D].杭州：浙江大学，2008.

[8]肖宏, 杨霞, 陈泽军,等. 赫兹接触理论在采用边界元法分析轧机轴承载荷中的应用[J]. 中国机械工程，2010，21(21)：2532-2535.

Xiao Hong, Yang Xia, Chen Zejun，et al. Application of Hertz Contact Theory in Analyzing Load Distribution of Mill Roller Bearing with Boundary Element Method[J]. China Mechanical Engineering, 2010,21(21): 2532-2535.

[9]高耀东.ANSYS机械工程应用精华50例[M].3版.北京：电子工业出版社，2011.

[10]郦正能，关志东，张纪奎，等.应用断裂力学[M].北京：北京航空航天大学出版社，2012.

[11]刘学平，庞祖富，向东.废旧塑封芯片分层裂纹仿真[J]. 中国机械工程, 2015，26(2)：143-146.

Liu Xueping, Pang Zufu, Xiang Dong. Simulation of Interfacial Delamination Crack of Waste Plastic Chips[J]. China Mechanical Engineering, 2015,26(2):143-146.

[12]Eriksson A, Nordmark A. Non-unique Response of Mooney-Rivlin Model in Bi-axial Membrane Stress[J]. Computers & Structures, 2014，144: 12-22.

[13]Morrell P R, Patel M, Skinner A R. Accelerated Thermal Ageing Studies on Nitrile Rubber O-rings[J]. Polymer Testing, 2003， 22(6):651-656.

(编辑袁兴玲)

收稿日期：2015-08-21

基金项目：国家重点基础研究发展计划(973计划)资助项目(2013CB035403)；国家自然科学基金资助项目(51375297)；国家高技术研究发展计划(863计划)资助项目(2012AA041803)；长安大学高速公路施工机械陕西省重点实验室开放基金资助项目(2014G1502044)

中图分类号：TP182

DOI：10.3969/j.issn.1004-132X.2016.12.001

作者简介：李琳，女，1989年生。上海交通大学机械与动力工程学院博士研究生。主要研究方向为故障诊断、TBM、损伤机理分析。张峰榕，男，1992年生。上海交通大学机械与动力工程学院硕士研究生。陶建峰，男，1975年生。上海交通大学机械与动力工程学院博士、副教授。刘成良，男，1964年生。上海交通大学机械与动力工程学院教授、博士研究生导师。

Analysis for Fracture of O-ring in Hang Hydraulic Cylinder of TBM Based on Fracture Mechanics

Li Lin Zhang FengrongTao Jianfeng Liu Chengliang

Shanghai Jiao Tong University,Shanghai,200240

Abstract：To study the causes for the fracture of the O-ring in the hang hydraulic cylinder of a TBM, the maximum stress which O-ring might withstand was analyzed with fracture mechanics under different Poisson’s ratios and the initial cracks. Stress distribution of the O-ring was simulated under the actual working conditions of TBM using ANSYS. The analysis results show that in the process of practical work of the TBM, due to the complicated working conditions, the local stress of O-ring will beyond the maximum stress that may sustain before the crack rapidly propagates and it will result in the fracture of O-ring. It indicates that a larger Poisson’s ratio of O-ring of hang hydraulic cylinder may be chosen in order to avoid the fracture based on the theoretical analyses and simulation results and the initial crack must be carefully controlled.

Key words：full face rock tunnel boring machine (TBM)； fracture mechanics； O-ring； fimite element simulation