基于遗传算法的三坐标测量机测量路径规划方法

周开俊　肖　轶　周小青

南通职业大学，南通，226007



基于遗传算法的三坐标测量机测量路径规划方法

周开俊肖轶周小青

南通职业大学，南通，226007

摘要：针对现有三坐标测量机检测路径规划方法的不足，提出和构建了零件检测特征群数学模型和求解流程，在此基础上，根据检测工作平面、检测测头及检测测针变动次数和检测路径构建优化目标函数，从宏观和微观两个层面分别应用矩阵交叉遗传算法和序列规划遗传算法进行零件检测特征路径的优化求解。最后以Hexagon公司检测零件为例，说明了零件初始检测信息的获取以及算法的优化求解过程。实践证明，该方法快速有效，且具有良好的工程应用价值。

关键词：三坐标测量机；测量路径规划；遗传算法；矩阵交叉；序列规划

0引言

随着装备制造业向智能化、集成化、高端化方向发展，越来越多的机械制造企业开始使用三坐标测量机进行零件质量的监测和检测。在单件测量中，测量路径往往是靠操作人员的经验和检测偏好进行的，是否是最短路径、是否是最短时间往往并不重要。然而在产品批量检测时，测量机运行的时间往往对检测成本有比较大的影响，同时也影响测量机的测量效率和自动化水平。因此如何规划出高效的测量机行走方案，一直是国内外研究人员的研究热点。

Ainsworth等[1]开发了一种测量路径规划系统，将CAD模型和采样点作为输入因子，利用开发的系统规划测量路径。Lee等[2]按特征的优先等级对特征进行分组，通过确定特征组的检测顺序和组内特征的检测顺序，生成了总体的检测规划。Albuquerque等[3]设计了一种自动的放置点和路径规划方法，通过放置点面的不断细分迭代，能够高效生成复杂零件的多个相交特征的无碰撞检查路径。Zhang等[4]开发了一种基于特征的三坐标测量工艺规划系统，系统分为公差分析、可达性检测、聚类算法、路径规划、检测工艺规划5个模块。Lu等[5]、纪晓刚等[6]通过在被测特征间引入过渡点，建立各点之间的关系矩阵，然后利用遗传算法求解测量了最短路径。王世刚[7]从工艺规划的角度，建立了测量路径优化的数学模型，利用遗传算法和禁忌搜索算法进行了优化求解。方忆湘等[8-9]以测点变换次数最少和路径最短作为优化目标，运用多色集理论建立了测头与待测特征之间的关系矩阵，利用现代优化算法对待测几何特征进行了测量排序。总的来说上述研究大都偏重于求解最短测量路径，而在三坐标实际测量过程中，某些同类或相近距离的特征互换测量顺序对测量时间和测量路径影响不大，因此无需按旅行者算法或其他优化算法寻找最短路径。

路径规划的目的并不仅仅是为了寻找一条最短的检测路径，而是使测量机在测量时间、测量路径和测量效益上达到一个综合的优化效果。本文以此为目标，建立检测特征群模型，根据检测工作平面、检测测头及检测测针变动次数和检测路径分别构建优化目标函数，从宏观和微观两个层面应用遗传算法寻找最优的检测方案。

1检测特征群模型的建立

三坐标测量机主要用来检测零件的尺寸、形状和位置精度，但是不管是尺寸、形状，还是位置精度，最终均是由零件上的各种特征综合形成和作用的结果，因此检测的对象或信息的收集主要是零件上的相关检测特征。一般来说，零件上的几何特征不外乎点、线、面、圆、圆柱、圆锥、球这几类特征。其中圆、圆柱、圆锥、球还有内外之分；曲线、曲面一般通过扫描轮廓点云来表示；而槽则是面、圆柱、圆锥等特征的复合体。精度检测的本质则是根据检测尺寸、形状和位置精度要求，按照一定的顺序和路径收集相关特征的信息，将同类检测特征放在一起检测，以期检测时间最短、坐标测量机的损耗最小、效益最高。

假设零件由n个关键特征组成，表示为F={F1,F2,…,Fn}(如果零件中存在多个相同的关键特征，在编号时以不同的编号加以标注)，被划分成s个检测群，表示为G={G1,G2,…,Gs}，每个检测群内的特征数量为ki，则有

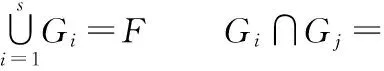
那么零件检测特征群可以用数学方法描述成如下形示：

(1)

记为

G=R·F

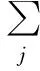
2检测初始信息获取

为了获取零件检测特征的信息，三坐标测量机的测头必须能无障碍地抵达被测特征表面。通常情况下，为了获得高质量的测量信息，测针应沿被测点的法向量方向前进，即应保证测针上红宝石球沿法向量方向与测点接触，因此需要预先定义特征的检测工作平面。根据笛卡儿坐标系，检测工作平面一般为立方体除底面以外的5个平面，当然也可根据具体情况，设置与5个平面成夹角的斜面。

目前，三坐标测量机上使用的测头分为两类：一类是可旋转式测头(自动/手动，可完成A/B轴旋转)；另一类是固定式测头，配自动更换架。不管是第一类还是第二类，在更换工作平面时，均需改变测针的工作角度，差别在于前者移动至安全位置完成角度变换，后者必须回更换架，更换相应的吸盘。一般情况下，零件的检测特征使用一种探针即可完成，但对于复杂零件，由于检测精度的要求和检测位置的限制，常常需要多根探针，此时可旋转式测头和固定式测头都需回更换架更换测针。

因此，在规划特征检测路径时，首先根据检测零件的几何结构、检测要求及使用三坐标测量机的特点确定各检测特征的工作平面、检测角度及使用的测针要求信息。为了便于表述，现采用数学映射关系进行描述，如下所示：

S(Fi)=Φ(Pi,Ai,Mi)

(2)

式中，S(Fi)为Fi特征所处的检测状态；Φ(Pi,Ai,Mi)为其检测状态的映射值；Pi为检测工作平面，其值为+Z、+X、+Y、-X、-Y5个检测工作平面的一种；Ai为测针检测角度，对于固定式测头其值为直立吸盘、五方位吸盘、角度吸盘当中的一种；Mi为使用的测针型号，根据零件的检测位置和检测精度选用，一般测针红宝石球直径从0.5～10 mm，长度从20～100 mm不等。

显然，式(2)的表达形式可很容易使用计算机进行表达，有利于后续的检测路径自动规划处理。

3零件特征检测路径规划流程

基于三坐标测量机的零件特征检测路径规划问题，实际上就是根据零件几何结构、检测要求和所用三坐标测量机的特点确定检测特征的先后顺序问题。该问题可以分解为两个部分：一是求解划分检测特征群的问题(宏观)，即哪些特征放在一起检测可使测量变换次数最少，也就是求解式(1)特征群划分矩阵的问题；二是求解所划分的检测特征群内特征的先后检测顺序的问题(微观)，即保证每个划分特征群内特征检测路径最短的问题。由于零件检测特征群矩阵R=(rij)s×n只存在0和1两种元素，且每列具有只有一个1的特点，互换检测特征群矩阵的列不仅可以改变特征群所属特征的组成和个数，而且不会违反相关的约束条件，因此可将零件检测特征群矩阵整体作为遗传算法的基因编码。另外，遗传算法与传统的优化方法(枚举、启发式等)相比较，在求解复杂问题时具有收敛性好、计算时间短、鲁棒性高等优点[10]，因此本文选用遗传算法进行求解。

图1所示为基于三坐标测量机的零件特征检测路径规划流程，检测人员首先根据零件几何结构、检测要求和三坐标测量机的特点建立零件检测特征群矩阵，获取相关检测初始信息，建立优化评价目标函数；然后利用矩阵交叉遗传算法求解划分检测特征群；最后利序列规划遗传算法顺序优化所获得的每个检测特征群，从而形成最终的优化规划检测路径。

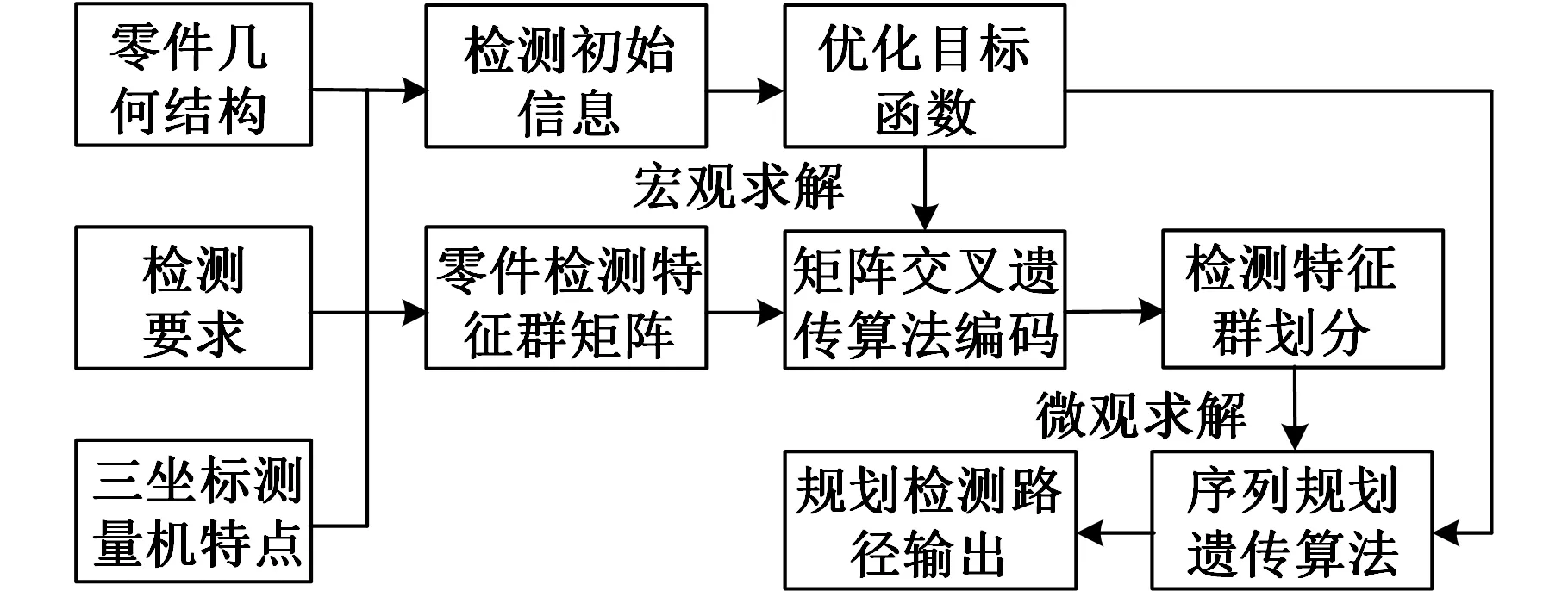
图1　基于三坐标测量机的零件特征检测路径规划流程

4适应度函数构造

为了获得质量比较高的检测路径规划，需要构造一个优化目标函数来度量不同检测路径规划方案的优劣。

4.1检测工作平面、更换测头及测针变动次数

对于某一个检测特征群Gj={…Fm，Fm+1…}，j=1,2,…，s，如果Φ(Pm,,)=Φ(Pm+1,,)，则令αi=1，反之则令αi=0；同理，如果Φ(,Am,)=Φ(,Am+1,)，则令βi=1，反之则令βi=0；如果Φ(,,Mm)=Φ(,,Mm+1)，则令γi=1，反之则令γi=0。其中i=1，2，…，ki。则整个特征群进行检测时需要改变检测工作平面、更换测头及测针的次数之和可表示为

n(G)=n(P)+n(A)+n(M)=

(3)

式中,n(P)、n(A)、n(M)分别为所有检测特征群改变检测工作平面、更换测头及测针的次数之和。

显然n(G)越小，完成特征序列检测时需要调整检测角度、更换检测测头和测针的次数越少，三坐标测量机的损耗越小，检测辅助时间越短。

4.2检测特征间行走路径

为了便于统计检测特征之间的行走路径，本文根据自动规划的要求作如下简化约定：①不管检测哪一个的特征，检测开始点均从该检测特征工作平面的设定安全距离处开始；②任一特征检测完毕后返回安全距离处再开始下一特征检测；③检测平面特征时，只计算安全距离处到达检测平面法向量上行走的距离；④圆柱、圆锥、圆孔、检测时，以其中心轴心与顶面的交点作为检测控制点进行计算；⑤球特征以球心作为检测控制点进行计算，尽管实际检测时可能存在干涉；⑥更换工作平面时，行走距离增加原工作平面及新工作平面的安全距离之和。

那么，对于某一个检测特征群序列Gj={…Fm，Fm+1…}，记特征Fm的检测来回距离为d(Fm)，工作平面的安全距离为ds(假定每个工作平面的安全距离一致，实际检测时按零件几何结构设置)。更换测头的距离比较远，一般也是因为工艺和检测要求需要，是必须行走的距离，因此不计入统计之中。则该特征群序列的总的检测行走距离为

(4)

显然，d(Gj)越小，遍列检测特征群Gj行走距离最短，检测过程中浪费的时间就最少。

4.3评价优化目标函数

根据第3节所述思路，在评价检测路径规划质量的过程中，当优化求解检测特征群划分问题(宏观)时，采用式(3)作为优化目标函数。为了使特征群的划分更接近工程实际，划分时要防止两种倾向，一是所有检测特征抱成一团，不作任何划分，全部放在一个群中；二是防止过度划分，一个检测特征单独划分为一个群。这两种现象，均失去了划分的意义，因此在划分时，对这两种现象均应作适当惩罚。即当s=1和s=n时，n(G)=n(G)+ζ，ζ为惩罚系数，一般取划分特征总数的2～3倍，这里取ζ=50。

当优化求解每个检测特征群内的特征的检测先后顺序的问题(微观)时，采用式(4)作为优化目标函数。在输出最终检测路径时应注意相邻两划分特征群的先后顺序，必需综合考虑前一检测群内最后一个特征的坐标位置和后一检测群内第一个特征的坐标位置，选择路径距离较短的检测群作为后续检测序列。

5遗传算法操作

5.1矩阵交叉遗传算法

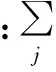
(2)交叉重组[11]。为了保证种群的交叉效果，采用两点部分列交叉并移位重组方法。随机在两交叉的染色体中选择一个交配区域，如两父代染色体及交配区域选定为A、B，然后将B的交配区域加到A的前面，A交配区域加到B的前面，再顺次后移即得到两子代染色体A′和B′，具体过程如图2所示。这种方法的优点是无需考虑父代染色体情况，获得的子代均会有一定程度的变异效果，有利于保持种群的多样化。

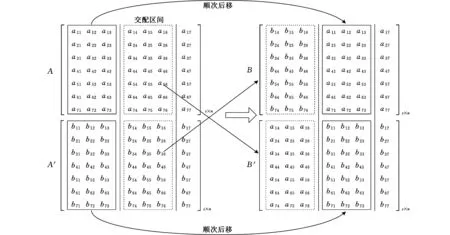
图2　两点部分列交叉并移位重组方法示意图

(3)变异技术。在设定的变异概率Pm下进行变异操作，一旦发生变异，即随机产生两个互换列的位置，对染色体的该两列进行互换，互换次数也随机产生。

5.2序列规划遗传算法

(1)编码。以检测特征群中检测特征的序号作为种群染色体的基因编码，种群的初始生成、交叉及变异操作保证检测特征群中各检测特征的序号只能出现一次，不得重复出现。

(2)交叉重组。采用如下的部分交叉重组方法[12]：①随机在种群染色体中选择一个交配区域，如两父染色体及交配区域选定为

A=1 2 | 3 4 5 6 | 7 8 9

B=9 8 | 7 6 5 4 | 3 2 1

②将B的交配区域加到A的前面或后面，A的交配区域加到B的前面或后面得

A′=7 6 5 4 | 1 2 3 4 5 6 7 8 9

B′=3 4 5 6 | 9 8 7 6 5 4 3 2 1

③在A′中自交配区域后依次删除与交配区相同的零部件编码，得到最终的两子染色体为

A″=7 6 5 4 1 2 3 8 9

B″=3 4 5 6 9 8 7 2 1

与其他方法相比，这种方法在两父染色体相同的情况下仍能产生一定程度的变异效果，这对维持群体内的多样化有一定的作用。交叉概率定为Pc。

(3)变异技术。每一代种群以变异概率Pm进行变异，一旦变异操作发生，则用随机方法产生交换次数K，对所需变异操作的染色体基因进行K次对换(对换的两基因位也是随机产生的)。

6应用实例分析

为尽可能多地体现各类测量特征，以Hexagon公司提供的测量零件为例，说明特征检测的路径规划过程。使用的三坐标测量机为Hexagon Global Classic SR 071007，配德国Leize公司LSP-X1C固定式扫描测头，装有三工位吸盘更换架，可装有90°、五方位、60°斜角吸盘，使用测针均为φ3 mm测针，如图3所示。图4为零件三维结构图，其特征信息如表1所示。该零件有外圆柱、外圆锥、外球、曲面、内圆柱、内圆锥、内球，覆盖+Z、+X、-X、+Y、-Y5个工作面，为了减少测头更换次数，主检测测头使用五方位吸盘，次检测测头使用60°斜角吸盘，根据测量要求一次性装好。

(a)使用仪器

(b)LSP-X1C固定式扫描测头图3　零件检测现场

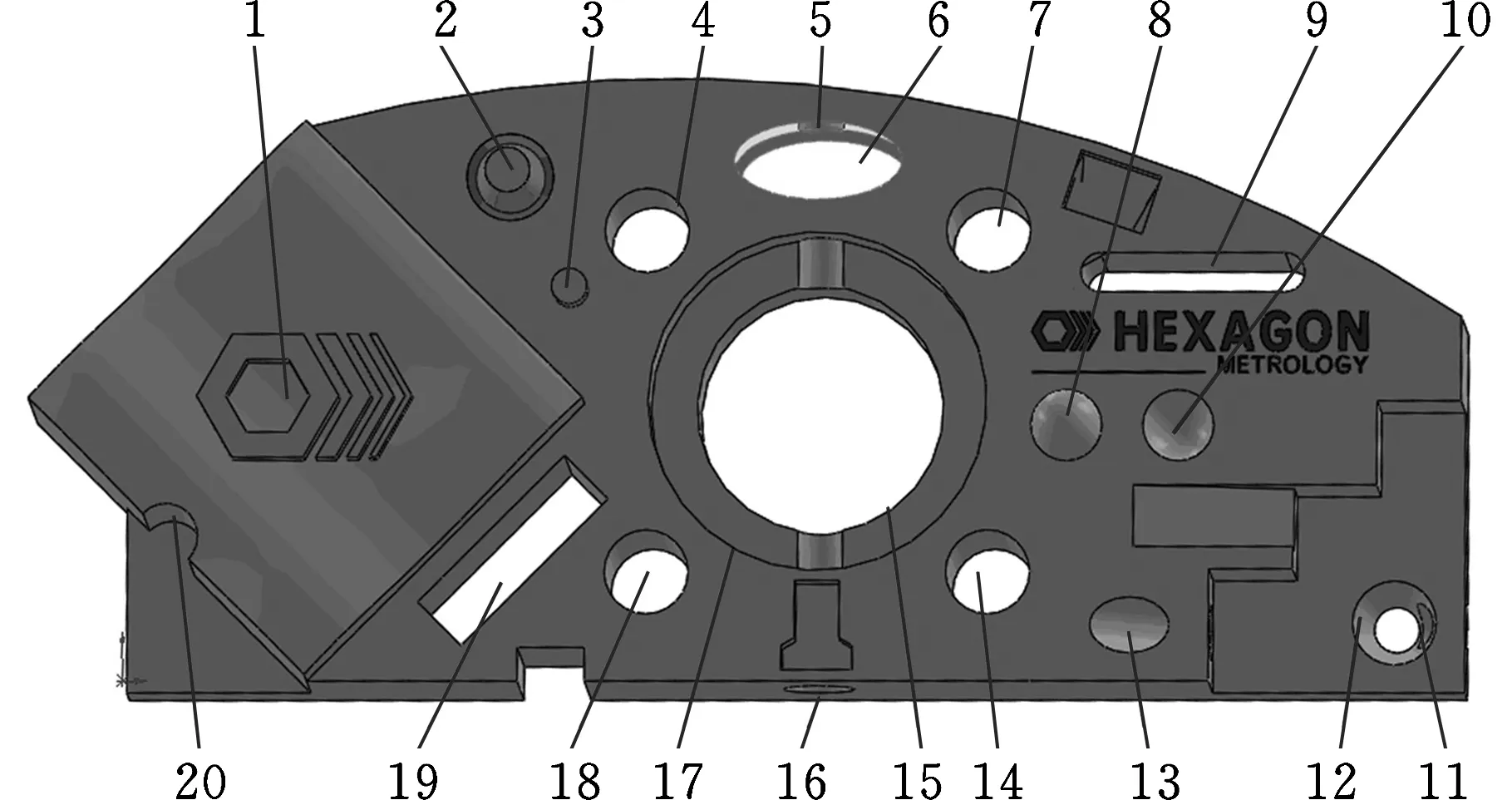
图4　零件三维结构图(各特征信息见表1)

表1为检测初始信息表，各工作面的安全距离均设为40 mm，测针直径均为3 mm;零件三维轮廓尺寸分别为：lx=256 mm，ly=108 mm，lz=60 mm。根据第5节所述的遗传算法操作方案，采用Borland C++编写了算法原型程序。在种群大小为100，交叉概率为0.85，变异概率为0.15时，矩阵交叉遗传算法于214代收敛，获得最佳特征群划分结果(因为是顺序解析，所以特征群内特征的顺序不代表检测顺序)：

(1 2 3 4 6 7 8 9 10 12 14 15 17 18 19 20)，

(16)，(11)，(5)，(13)

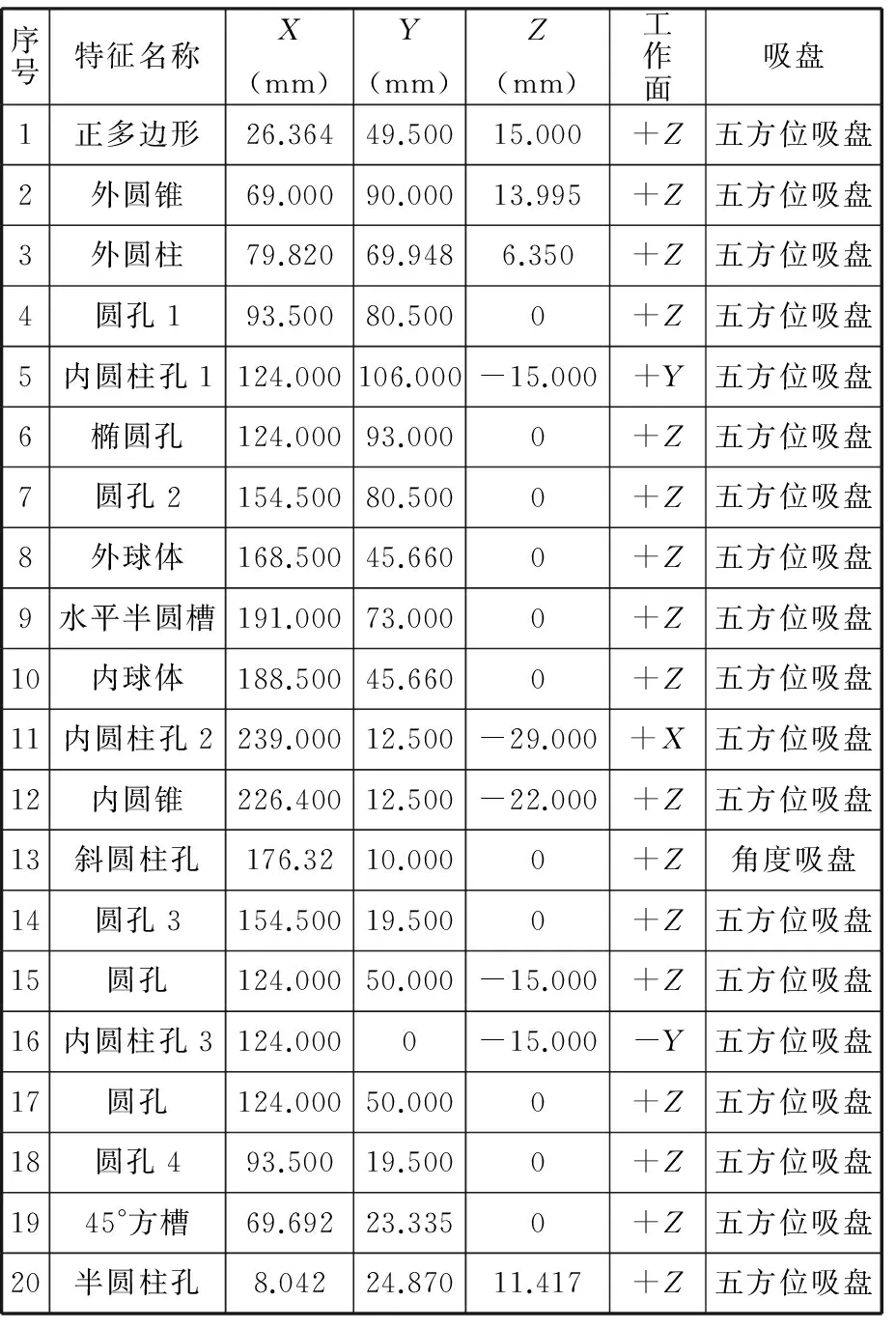
表1　零件初始信息表

再将特征群划分结果输入序列规划遗传算法，在种群大小为100，交叉概率为0.55，变异概率为0.45时，算法于360代收敛，获得最优检测顺序如下：

20→1→19→18→17→15→14→12→10→8→

9→7→6→4→3→2→5→11→16→13

表2为优化路径与几种典型检测路径的对比分析表。三坐标测机开机后需要进行测头校准，角度吸盘需在+Z方向校核完成的基础上再进行校核，另外在进行特征检测之前需要建立手工和DCC坐标系，必须由带有+Z方向测针的吸盘完成，因此在完成上述过程后正式进行特征检测时，三坐标上的吸盘是带有+Z方向的吸盘，本例中即为五方位吸盘，此时直接进行角度特征检测，会增加吸盘更换的次数。由表2可看出，本文算法优化获得的结果在更换吸盘次数、检测工作平面变动次数及测头行走距离上均具有较大的优势，说明本文优化结果与工程实际情况基本吻合，算法具有较好的普适性和工程应用价值。

7结语

零件检测特征群模型和求解流程揭示了零件特征检测路径规划的本质，规划人员可根据检测批量和检测要求，结合使用三坐标仪器现状，有侧

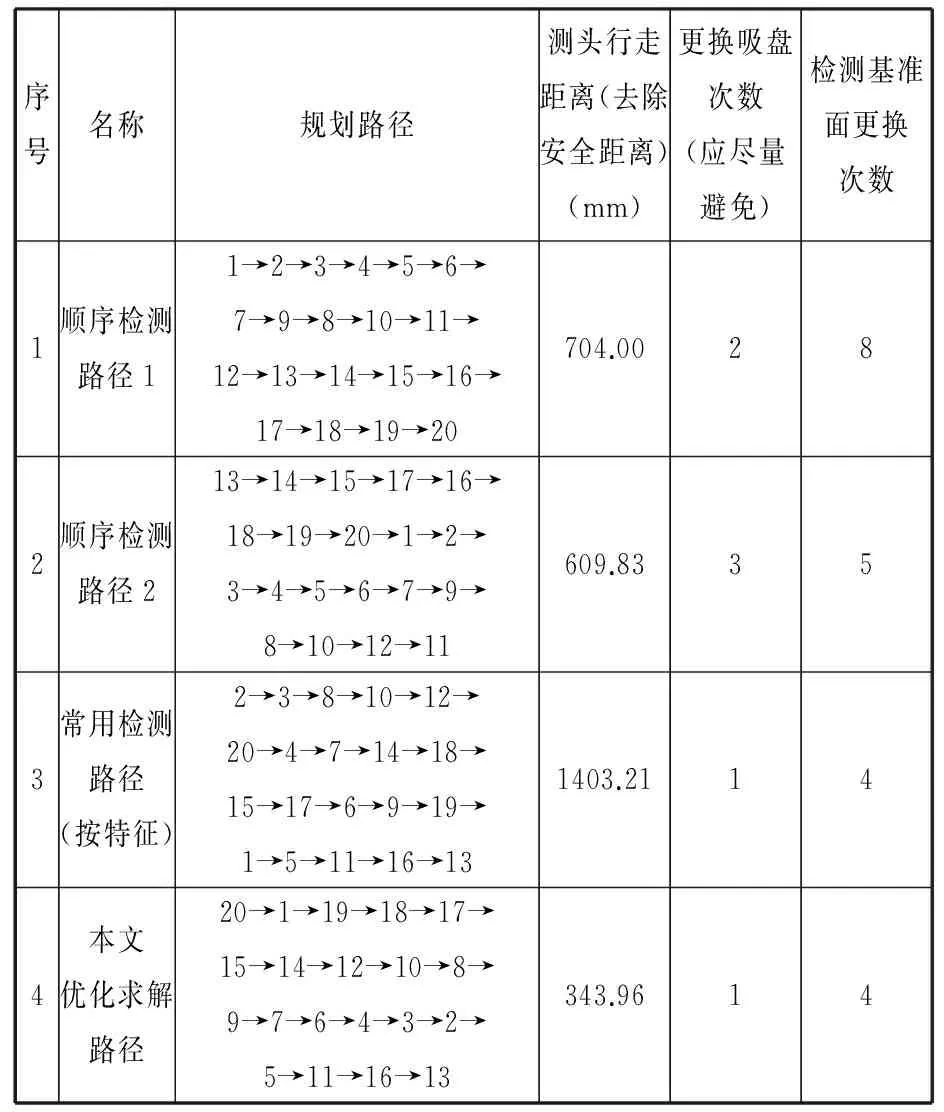
表2　优化检测路径与几种典型路径的对比分析

重地提取零件检测初始信息，如检测角度变化对检测精度影响大，更换检测测头效率低时，应偏重于检测特征群的合理划分，否则应偏重于检测路径的距离，在难以取舍时应两者并重，利用矩阵交叉遗传算法求解零件检测特征群，再利用序列规划遗传算法求解群内特征的检测顺序。实践证明该方法快速有效，且具有较高的工程应用价值。

参考文献：

[1]AinsworthI，RisticM,BrujicD.CAD-basedMeasurementPathPlanningforFreeformShapesUsingContactProbes[J].InternationalJournalofAdvancedManufacturingTechnology, 2000, 16:23-31.

[2]LeeHonghee,Myeong-WooC,Gil-SangY,etal.AComputer-aidedInspectionPlanningSystemforOn-machineMeasurement-PartI:GlobalInspectionPlanning[J].KSMEInternationalJournal, 2004, 18(8):1349-1357.

[3]AlbuquerqueVA,LiouFW,MitchellOR.InspectionPointPlacementandPathPlanningAlgorithmsforAutomaticCMMInspection[J].InternationalJournalofComputerIntegratedManufacturing, 2000, 13(2):107-120.

[4]ZhangSG,AjmalA,WoottonJ,etal.AFeature-basedInspectionProcessPlanningSystemforCo-ordinateMeasuringMachine(CMM)[J].JournalofMaterialsProcessingTechnology, 2000, 107:111-118.

[5]LuCG,MortonD,WuMH,etal.GeneticAlgorithmModelingandSolutionofInspectionPathPlanningonaCoordinateMeasuringMachine(CMM)[J].TheInternationalJournalofAdvancedManufacturingTechnology, 1999, 15:409-416.

[6]纪小刚，龚光容. 三坐标测量机中基于遗传算法的多特征测量路径规划研究[J]. 兵工学报, 2005,26(3):392-396.

JiXiaogang,GongGuangrong.GeneticAlgorithmBasedMulti-characterInspectionPathPlanninginCoordinateMeasuringMachines[J].AcatArmamentarii, 2005, 26(3):392-396.

[7]王世刚. 基于CMM测量路径优化算法的研究[J]. 机械科学与技术, 2005，24(5):606-608.

WangShigang.ResearchonCMM-basedAlgorithmofMeasurementPathOptimization[J].MechanicalScienceandTechnology, 2005, 24(5):606-608.

[8]方忆湘，杨克强，黄风山.CMM测量中复杂零件的路径规划研究[J]. 制造业自动化, 2013，35(3):36-40.

FangYixiang,YangKeqiang,HuangFengshan.ResearchaboutComplexPartsMeasuringPathPlanningofCMM[J].ManufacturingAutomation, 2013, 35(3):36-48.

[9]黄风山，方忆湘，姜腾，等. 规则约束和蚁群算法三坐标测量路径规划研究[J]. 机械设计与制造, 2014(9):201-204.

HuangFengshan,FangYixiang,JiangTeng,etal.InspectionPathPlanningBasedonRulesandAntColonyAlgorithmforCoordinateMeasuringMachine[J].MachineryDesignandManufacture, 2014(9):201-204.

[10]邢文训，谢金星. 现代优化计算方法[M]. 北京：清华大学出版社，2001.

[11]周开俊，贡智兵，童一飞. 面向再设计的产品模块划分方法[J]. 中国机械工程， 2015，26(15):2096-2102.

ZhouKaijun,GongZhibing,TongYifei.AModulePartitionMethodforProductRedesign[J].ChinaMechanicalEngineering,2015,26(15):2096-2102.

[12]周开俊，李东波，黄希. 基于遗传算法的装配序列规划方法[J]. 机械设计，2006，23(2)：30-32.

ZhouKaijun,LiDongbo,HuangXi.AssemblySequencePlanningBasedonGeneticAlgorithm[J].JournalofMachineDesign, 2006，23(2)：30-32.

(编辑袁兴玲)

收稿日期：2015-08-25

基金项目：江苏省青蓝工程资助项目(2014)；南通市科技计划资助项目(CP22013002，BK2014027)

中图分类号：TP391

DOI：10.3969/j.issn.1004-132X.2016.12.012

作者简介：周开俊，男，1974年生。南通职业大学机械工程学院副教授、博士。主要研究方向为先进制造技术等。获省部级科技进步二等奖1项。发表论文20余篇。肖轶，男，1980年生。南通职业大学机械工程学院副教授，博士。周小青，男，1974年生。南通职业大学机械工程学院副教授，博士。

AMethodforCMMInspectionPathPlanningBasedonGA

ZhouKaijunXiaoYiZhouXiaoqing

NantongVocationalUniversity,Nantong，Jiangsu，226007

Abstract:In order to improve the defects in present methods of CMM inspection path planning, a part measuring feature group model and solution processes were proposed. Then according to the characteristics of the mathematical model, a fitness function module was constructed based on the changing times of working planes, inspection angles, checking probe and the distance of detection paths. From macro and micro angles, the matrix crossover GA and sequence planning optimization GA were applied for solving optimization of inspection path planning. Finally, taking testing part of Hexagon Company for an example, the part initial checking data was acquired as well as the optimization algorithm for solving process was described. Practice proved that this method is fast and effective with good engineering application values.

Key words:coordinate measuring machine(CMM); inspection path planning; genetic algorithm(GA); matrix-cross; sequence planning