阿基米德斜撑离合器楔块型面修形设计及其性能分析

严宏志　赵　聪　刘志辉　张诗颖　王祎维

中南大学高性能复杂制造国家重点实验室，长沙，410012



阿基米德斜撑离合器楔块型面修形设计及其性能分析

严宏志赵聪刘志辉张诗颖王祎维

中南大学高性能复杂制造国家重点实验室，长沙，410012

摘要：在建立不同初始内楔角阿基米德型面模型基础上，对离合器接触性能(Hertz应力、周向应力、总变形)进行了分析，并与三圆弧型面离合器进行了对比。为了提高阿基米德型面斜撑离合器承载性能，通过增大其初始内楔角对阿基米德楔块型面进行修形，并对修形后离合器的接触性能进行了分析。分析结果表明：增大修形系数μ能减小接触应力，提高离合器强制连续的临界扭矩。此外，从自锁条件分析得到了最大修形系数μmax。

关键词：斜撑离合器；修形；阿基米德曲线；接触性能

0引言

强制连续约束(PCE)型斜撑式超越离合器由楔块、内环、外环、保持架和弹簧组成，具有承载能力强，使用寿命长，过载防“翻滚”的特点。

目前使用的PCE型斜撑离合器楔块上下凸轮曲线均为单圆弧型，这种型面存在楔合时间长，楔入冲击力大等[1]问题。由此，一些学者对不同斜撑块曲面结构与参数进行了研究。Xu等[2]对斜撑离合器的数学模型进行了研究，分析了楔块结构与接触性能的关系。胡大国[3]研究了对数螺线超越离合器工作楔角及承载能力的计算方法。张永岗等[4]对阿基米德螺旋超越离合器楔角进行了研究。严宏志等[5]对阿基米德曲面斜撑离合器动力特性进行了分析。严宏志等[6]对斜撑离合器楔块进行了疲劳寿命分析与结构优化。李志杰等[7]对超越离合器的滚柱进行了优化设计。段全心[8]对滚柱轴承离合器参数进行了分析与优化。郭惠昕等[9]对楔块式单向超越离合器结构参数进行了模糊优化。

研究表明，阿基米德斜撑离合器的楔块与内外环的最大楔入冲击力远小于单圆弧斜撑离合器的最大楔入冲击力，因此可减少楔块的磨损，延长离合器的使用寿命[5]。但由于阿基米德斜撑离合器的楔块型面内楔角υ在楔入加载过程中逐渐减小，降低了离合器的承载能力，可能导致离合器过早强制连续，因此本文以改善阿基米德斜撑离合器的楔块和内滚道接触性能，提高楔块寿命和离合器承载能力为目标，对阿基米德曲面斜撑块进行修形研究，为斜撑离合器楔块型面设计提供依据。

1不同初始内楔角的阿基米德斜撑离合器接触性能分析

斜撑离合器在楔入加载过程中上凸轮的接触应力小于下凸轮的接触应力[10]，在实际使用过程中，离合器的主要失效形式为下凸轮的材料剥落。因此，为了简化力学模型公式，上凸轮曲线仍采用单圆弧。阿基米德斜撑离合器的几何参数如图1所示。

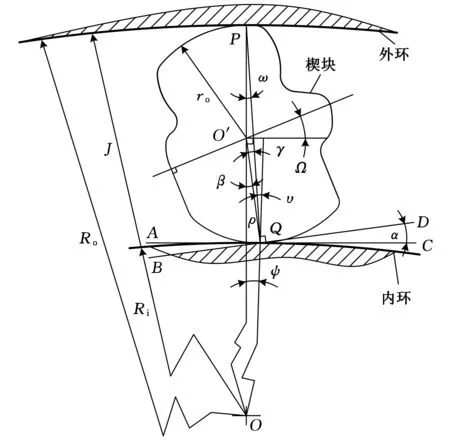
图1　阿基米德型面离合器几何模型

图1中，楔块下凸轮为阿基米德曲线，P、Q两点分别为楔块与内外环的相切点。OQ与PQ的夹角为内楔角υ，OP与PQ的夹角为外楔角ω，AC为Q点切线，BD为O′Q的垂线，AC与BD的夹角为α，O′Q为阿基米德螺线的初始接触极径ρ，O′Q与OP的夹角为β，OQ与OP的夹角为ψ，O′Q与PQ的夹角为γ，PQ长为l，Ω为楔块转角，ro为楔块上凸轮半径，Ro为离合器外环内径，Ri为离合器内环外径。

在满足阿基米德斜撑离合器设计基本要求[5]的条件下，对不同初始内楔角υ0的阿基米德斜撑离合器的接触性能进行分析。

1.1不同初始内楔角的楔块下凸轮阿基米德曲线参数求解

阿基米德曲线方程为

ρ=ρ0+aθ

(1)

其中，ρ为阿基米德曲线极径，θ为阿基米德曲线接触极角，ρ0为阿基米德曲线初始极径，a为阿基米德曲线系数，ρ0与a统称为阿基米德参数。

阿基米德参数求解需满足三个条件：自锁条件、溜滑角条件和有效楔块凸轮升程条件[5]。

由图1中的几何关系，得到如下关系式：

(2)

ψ=υ-ω

(3)

(4)

(5)

θ1=1.5π+β-Ω

(6)

α=ψ+β

(7)

a=ρ1tanα

(8)

ρ0=ρ1-aθ1

(9)

其中，θ1为阿基米德曲线初始接触极角。

在已知内楔角υ0、内环外径Ri、外环内径Ro、上凸轮半径ro和初始转角Ω的情况下，通过以上公式可求出阿基米德参数a、ρ0。

斜撑离合器在润滑状态下，楔块与内外滚道之间摩擦因数一般为0.08～0.1。在满足自锁条件下，υ应小于5.7°[11]。设计的楔角应使斜撑离合器能顺利进行楔合和脱楔。在此取不同初始内楔角υ0为3.3°、3.6°、3.9°、4.2°、4.5°，构建不同的阿基米德曲线，如表1所示。

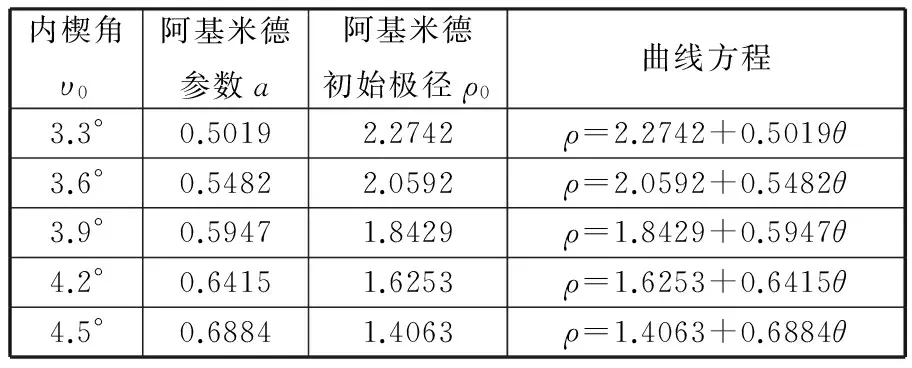
表1　不同初始内楔角对应的阿基米德曲线参数方程

1.2不同初始内楔角的阿基米德斜撑离合器接触性能

通过解析求解[12]，得到不同初始内楔角下离合器的极限工作扭矩Tmax，如图2所示。从图2中可知，增大初始内楔角υ0能够提高离合器的承载能力。

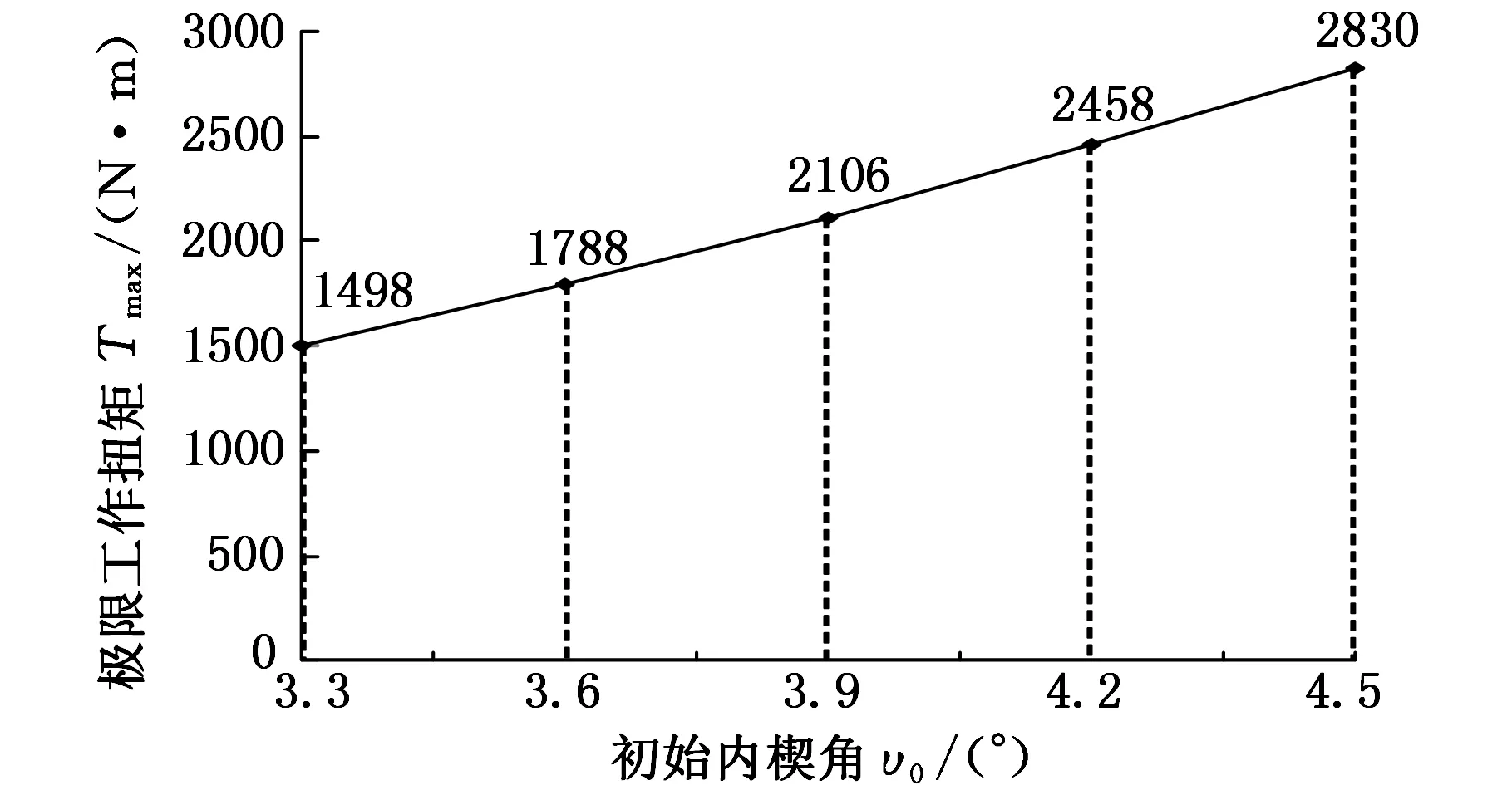
图2　不同初始内楔角的阿基米德离合器极限工作扭矩

在工作扭矩T=1498 N·m条件下，选取楔块数目n=41，楔块有效长度ls=21.6，解析求解，得到不同初始内楔角的阿基米德离合器接触性能如图3所示。从图3中可知，在相同工况条件下，增大初始内楔角υ0能改善离合接触性能。

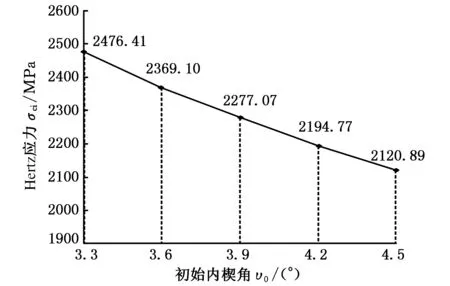
(a)楔块下凸轮与内环滚道之间的Hertz应力

(b)内环的周向应力

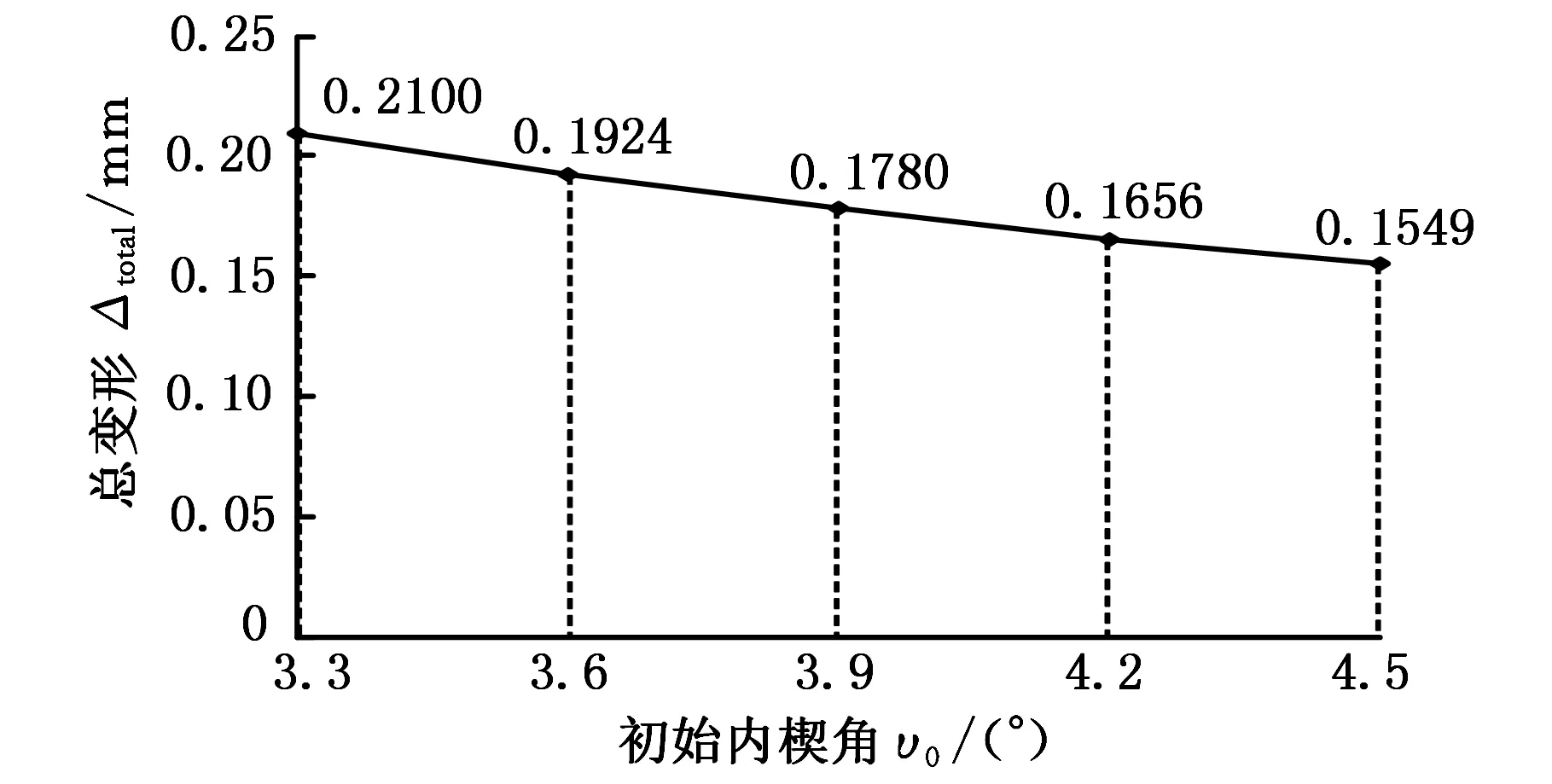
(c)楔块和滚道的总体变形图3　不同初始内楔角的阿基米德离合器接触性能

图4为阿基米德斜撑离合器在楔入加载过程中的内楔角变化曲线。从图4中可知，在楔入加载下阿基米德斜撑离合器的内楔角υ是逐渐减小的，而三圆弧斜撑离合器内楔角υ逐渐增大，这一性质使得阿基米德斜撑离合器在楔合过程中内环周向应力σi、楔块Hertz应力增大得很快，并且使得离合器临界过载扭矩较小，过早强制连续。

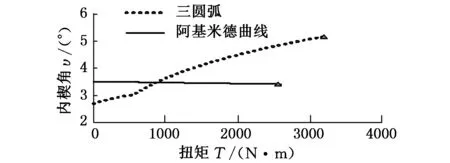
图4　不同型面离合器楔入加载时内楔角变化情况

2阿基米德斜撑离合器楔块型面修形

由于增大初始内楔角υ0能改善离合器接触性能，因此阿基米德斜撑离合器楔块型面修形的目标是：在保持较大的初始内楔角υ0条件下，使其在楔入加载过程中楔角逐渐增大。

为了使阿基米德斜撑离合器楔块在楔入加载过程中内楔角υ逐渐增大，则需要使楔块升程随着极角θ的增大而增大，由此建立修形模型为：ρ=ρ0+aθ+μθ2，如图5所示。

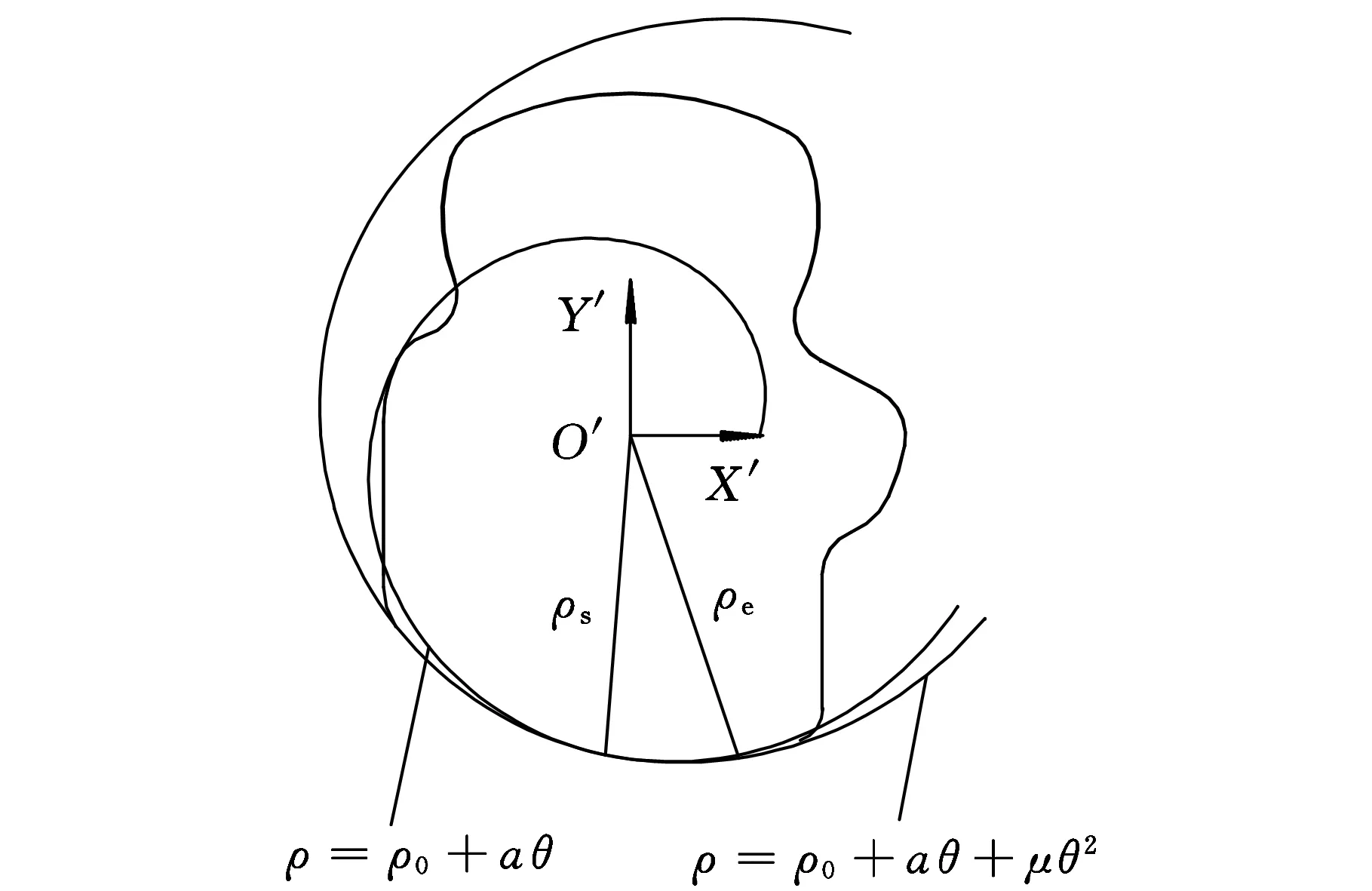
图5　修形曲线楔块型面模型

在保持初始内楔角υ0=3.9°不变的情况下，通过改变修形系数μ得到不同曲线方程如表2所示。

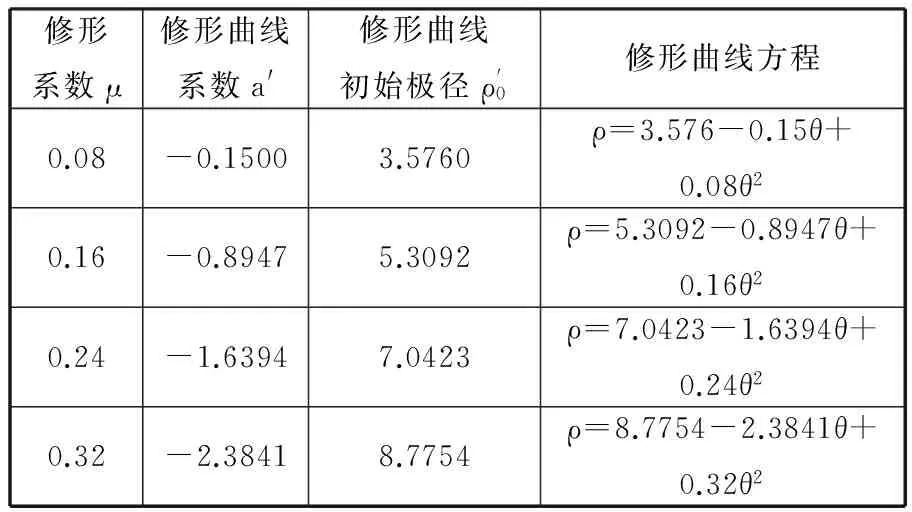
表2　初始内楔角υ0=3.9°下不同修形系数μ对应的曲线方程

3修形阿基米德斜撑离合器力学模型的建立

通过Hertz理论与厚壁圆筒理论对斜撑离合器进行力学分析，导出接触力学方程，通过解析法求出离合器楔块接触Hertz应力、内外环周向应力、总体变形等接触性能曲线。

3.1基本假设

为了进行力学分析，作如下假设：①应力以及外环和内环的变形由厚壁圆筒理论导出，外环材料的强化效应延伸到超过斜撑块的长度时可予以忽略；②由于斜撑块数目较多，其多边形效应小，故斜撑块的径向载荷可转换成等效的流体压力；③斜撑块的离心力作用在外套的载荷忽略不计；④假定内外滚道在初始载荷时处于同轴位置；⑤所有斜撑块载荷相等。

3.2力学模型的建立

斜撑块与内外环的接触关系按圆柱体接触理论来计算。在给出离合器内外环半径与斜撑块的结构尺寸后，可以按下列步骤进行迭代计算，求出楔角υ与ω，通过楔角υ、ω就可以求出楔块Hertz应力、内外环周向应力和总体变形[10]。

(1)计算

(10)

(2)计算

(11)

(3)计算

ρ=ρ0+aθ+μθ2

(12)

(4)计算

(13)

(5)计算

ω=υ-ψ

(14)

(6)计算

(15)

(7)计算

(16)

(8)计算

Ω=1.5π+β-θ

(17)

(9)计算

(18)

(10)计算

(19)

(11)计算

(20)

(12)计算

(21)

(13)计算

(22)

一般迭代10次左右就可以得到收敛值。

4接触性能求解结果与分析

对修形曲线斜撑离合器力学模型进行解析求解，得到了不同修形系数μ条件下斜撑离合器楔块Hertz应力、周向应力σi、总体变形和内楔角υ的变化情况。

4.1Hertz应力分析

如图6所示(“▲”表示强制连续点)，在离合器总体结构尺寸相同的条件下，无修形的阿基米德基本曲线产生强制连续的临界扭矩为2100N·m。随着修形系数μ的增大，强制连续点右移，强制连续临界扭矩逐渐增大，离合器能承受更大的载荷。当修形系数μ=0.32时，强制连续临界扭矩为3700N·m,在工作扭矩为2400N·m时离合器处于正常楔合状态；在相同工作扭矩条件下，增大修形系数能够减小楔块下凸轮接触Hertz应力。

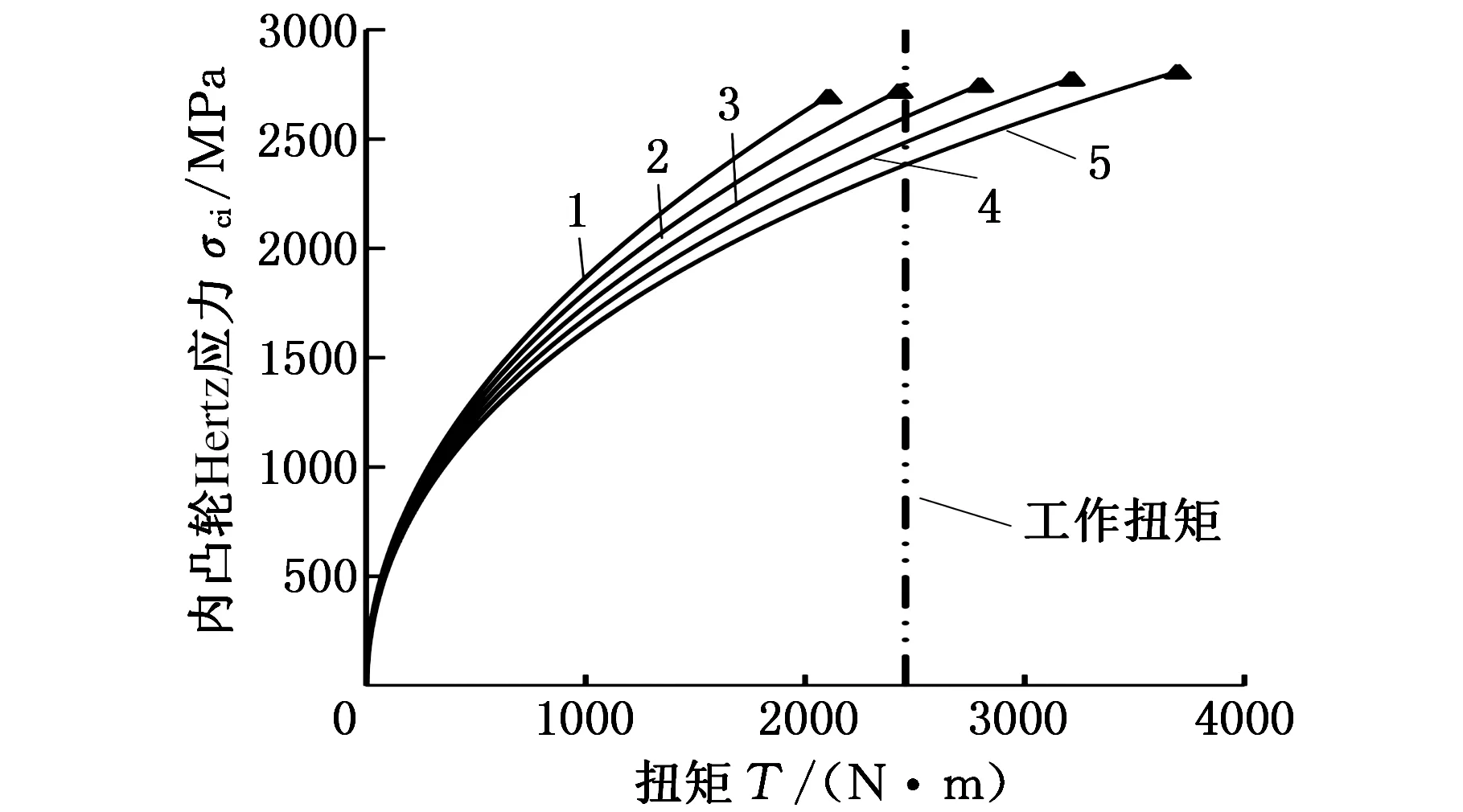
1.υ0=3.9°基本曲线　2.μ=0.08　3.μ=0.16 4.μ=0.24　5.μ=0.32图6　不同修形系数μ下的斜撑离合器楔块Hertz应力随扭矩增大的变化情况

4.2周向应力分析

如图7所示，未强制连续时，在相同工作扭矩下，增大修形系数μ能够减小内环周向应力。

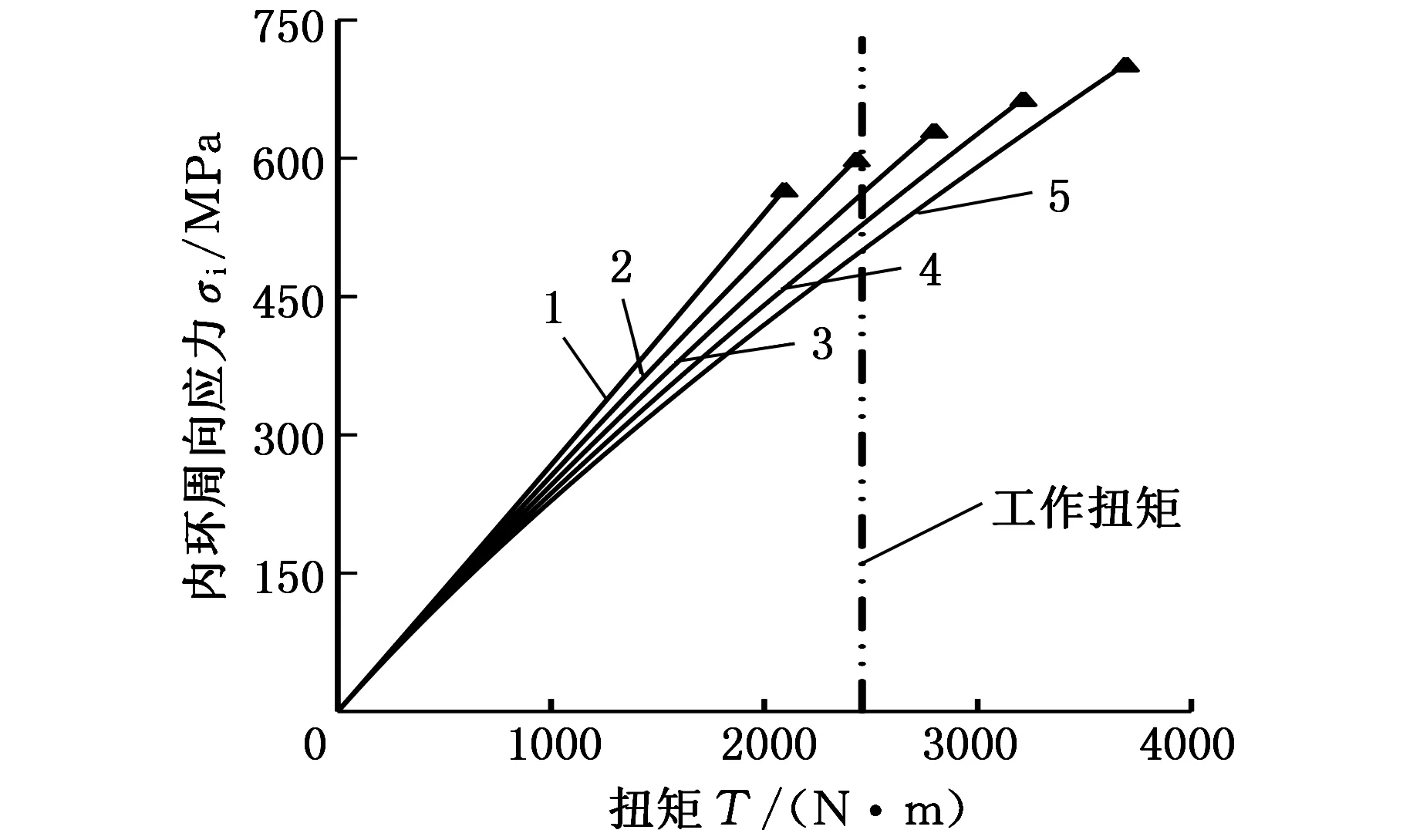
1.υ0=3.9°基本曲线　2.μ=0.08　3.μ=0.16 4.μ=0.24　5.μ=0.32图7　不同修形系数μ下的斜撑离合器内环周向应力随扭矩增大的变化情况

4.3总体变形分析

如图8所示，在未强制连续时，在相同工作扭矩下，增大修形系数μ能够减小离合器的总体变形。

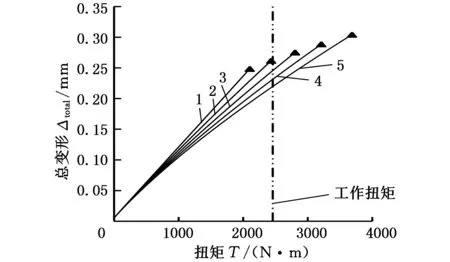
1.υ0=3.9°基本曲线　2.μ=0.08　3.μ=0.16 4.μ=0.24　5.μ=0.32图8　不同修形系数μ下的斜撑离合器体变形随扭矩增大的变化情况

4.4楔角分析

图9所示为楔块下凸轮内楔角υ在楔入加载过程中的变化曲线。由图9可知，在初始接触楔角υ0=3.9°情况下，阿基米德基本曲线斜撑离合器随扭矩增大内楔角υ递减；当增大修形系数μ后，随扭矩增大内楔角υ递增，随着修形系数μ的增大曲线斜率逐渐增大，从前述可知，接触加载过程中，内楔角逐渐增大能够改善离合器的接触性能。但由于楔角过大会降低离合器楔块的自锁能力，楔块容易打滑，因此，内楔角不能大于5.7°。

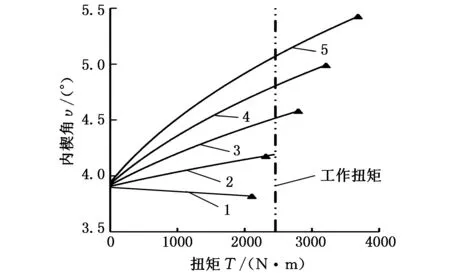
1.υ0=3.9°基本曲线　2.μ=0.08　3.μ=0.16 4.μ=0.24　5.μ=0.32图9　不同修形系数μ下的斜撑离合器内楔角υ随扭矩增大的变化情况

4.5满足自锁条件的修形系数μ

通过比较不同修形系数μ曲线的接触性能可知，在未强制连续时，在相同工况条件下，增大修形系数μ能够减小斜撑块Hertz应力、内环周向应力和离合器的总体变形，改善离合器的接触性能。此外，增大修形系数μ还能使强制连续临界扭矩增大，增大离合器的承载能力，避免离合器过早强制连续。由于受到楔块自锁条件约束，内楔角υ应小于5.7°，由于修形曲线的楔角在接触加载中逐渐增大，因此在产生强制连续的临界点处楔块的楔角最大。图10所示为不同修形系数μ下强制连续临界点处的楔角变化曲线，拟合的曲线方程为：υ=5.0426μ+3.792，由υ<5.7°得μ<0.378，即最大修形系数μmax=0.378。

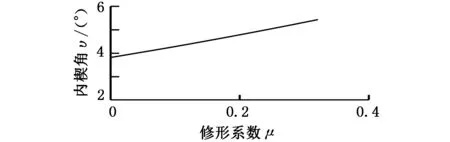
图10　强制连续临界点处阿基米德斜撑离合器内楔角υ随不同修形系数μ的变化

5结论

(1)阿基米德斜撑离合器在楔入加载过程中楔角逐渐减小，使得楔块Hertz应力、内环周向应力增大得很快，并且使得离合器临界过载扭矩较小，过早强制连续。

(2)增大阿基米德离合器初始内楔角υ0能够改善离合器的接触性能，增大离合器承载能力。

(3)增大修形系数μ能增大离合器强制连续点处的临界扭矩，增大离合器的承载能力，延长离合器的使用寿命，避免离合器过早强制连续。

(4)在未强制连续时，增大修形系数μ能减小楔块Hertz应力、内环周向应力和离合器的总体变形。

(5)在满足自锁条件的前提下，μ应小于0.378。

参考文献：

[1]严宏志，杨兵，胡魁贤，等.单圆弧PCE型离合器楔合过程力学特性分析[J].煤炭学报，2010，35(6)：1034-1038.

YanHongzhi,YangBing,HuKuixian,etal.MechanicalContactQualityAnalysisofEngagingProcessoftheSingleArcPCE-typeClutch[J].JournalofChinaCoalSociety,2010,35(6):1034-1038.[2]XuG,LowenG.AMathematicalModelofanOver-runningSpragClutch[J].MechanismandMachineTheory, 1994,29(1):11-23.[3]胡大国.对数螺线超越离合器的楔角计算[J].火炮发射与控制学报,1996(1):23-33.

HuDaguo.TheCalculationofLogarithmicSpiralClutchWedgeAngle[J].JournalofGunLaunch&Control,1996(1):23-33.

[4]张永岗，姚文席．阿基米德螺旋超越离合器的楔角研究[J]．研究探索，2000(11)：17-18.

ZhangYonggang,YaoWenxi.SurveyofWedgeAngleoftheArchimedeanSpiralOverrunningClutch[J].Research&Discussion,2000(11):17-18.

[5]严宏志，吴凯，何明生．阿基米德曲面楔块的PCE型离合器动力学特性分析[J]．机械设计，2011，28(4)：31-35.

YanHongzhi,WuKai,HeMingsheng.DynamicAnalysisofArchimedesCurvedSurfaceWedgePCEClutch[J].JournalofMachineDesign,2011,28(4):31-35.

[6]严宏志，顾俊，何明生．强制连续约束超越离合器楔角疲劳寿命分析及楔块结构优化[J]．机械科学与技术，2011，30(11)：1965-1972.

YanHongzhi,GuJun,HeMingsheng.FatigueLifeAnalysisandStructuralOptimizationofPCEClutchSprag[J].MechanicalScienceandTechonologyforAerospaceEngineering,2011,30(11):1965-1972.

[7]李志杰，石光林，温全明．超越离合器鼓形滚柱的优化设计[J]．机械传动，2013，37(4)：53-59.

LiZhijie,ShiGuanglin,WenQuanming.OptimizationDesignoftheDrumRolleroftheOverrunningClutch[J].JournalofMechanicalTransmission,2013,37(4):53-59.

[8]段全心.滚柱轴承离合器参数分析及优化[D].太原：太原科技大学，2008.

[9]郭惠昕，吴晓，张龙庭．楔块式单向超越离合器结构参数的模糊优化设计[J]．机械设计，2001(2)：25-27.

GuoHuixin,WuXiao,ZhangLongting.FuzzyOptimizationDesignoftheStructureParametersofSpragOverrunningClutch[J].JournalofMachineDesign,2001(2):25-27.

[10]朱楚，朱如鹏，靳广虎. 对斜撑超越离合器力学性能的影响分析[J].机械制造，2012,41(5)：11-20.

ZhuChu,ZhuRupeng,JinGuanghu.AnalysisofEffectsonMechanicalPropertiesofSpragOverrunningClutch[J].Machinery, 2012,41(5)：11-20.

[11]卿茂辉.对数型面楔块斜撑离合器接合特性及磨损寿命分析[D].长沙：中南大学，2014.

[12]朱楚.高速斜撑超越离合器设计方法研究[D].南京：南京航空航天大学，2012.

(编辑王艳丽)

收稿日期：2015-07-27

基金项目：湖南省科技计划资助重点项目(2015JC3007)

中图分类号：TH133.4

DOI：10.3969/j.issn.1004-132X.2016.12.007

作者简介：严宏志，男，1964年生。中南大学机电工程学院研究员、博士研究生导师。主要研究方向为复杂曲面高速高精数字制造理论与技术、机电装备监控理论与技术、高速航空离合器设计制造的理论与技术。发表论文110余篇。赵聪，男，1989年生。中南大学机电工程学院硕士研究生。刘志辉，男，1984年生。中南大学机电工程学院博士研究生。张诗颖，女，1991年生。中南大学机电工程学院硕士研究生。王祎维，男，1991年生。中南大学机电工程学院硕士研究生。

ModificationDesignandContactPropertyAnalysisforProfilesofArchimedesTypeSpragClutch

YanHongzhiZhaoCongLiuZhihuiZhangShiyingWangYiwei

StateKeyLaboratoryofHighPerformanceComplexManufacturing，CentralSouthUniversity，Changsha,410012

Abstract:Contact properties of Archimedes type sprag clutch (including Hertz stress, circumferential stress and total deformation) were analyzed and compared with three-arc type sprag clutch on the basis of different initial inner wedge angle models. To improve the bearing capacity of Archimedes type sprag clutch, modification on sprag profile of Archimedes was conducted by increasing the initial inner wedge angle, and contact properties of clutch were analyzed after modification; The results show that contact stress is reduced and the critical torque is improved when increasing modification coefficient. Moreover, the maximum modification coefficient μ is obtained from self-locking condition analysis.

Key words:sprag clutch; modification; Archimedes curve; contact property