基于ISOMAP降维的复杂轮廓异常点识别方法

聂　斌　李京亚　姚雪海

天津大学，天津，300072



基于ISOMAP降维的复杂轮廓异常点识别方法

聂斌李京亚姚雪海

天津大学，天津，300072

摘要：高维复杂轮廓异常点识别方法研究是目前过程轮廓监控的重要课题之一。以高维复杂轮廓为研究对象，建立非参数轮廓矩阵模型，将基于测地距离的ISOMAP非线性降维技术与χ2控制图相结合，提出新的轮廓异常点识别方法，以实现高维复杂轮廓异常点的准确识别。仿真实验和实际案例的应用分析结果证实该方法在异常点识别的准确性方面具有良好的性能。

关键词：异常点识别；等距特征映射(ISOMAP)；轮廓；降维

0引言

统计过程控制(statisticqualitycontrol,SPC)是一种借助数理统计理论对过程进行控制的方法。SPC可以在过程中及时发现问题，确定过程稳定性，以保证最终产品的质量。Woodall等[1]和Hawkins等[2]将SPC过程分为两个重要阶段：第一阶段以采集到的历史数据作为基础，建立稳定运行状态模型；第二阶段根据已有的模型，在制造过程中，对实时数据逐个进行监控，及时发现动态过程中的变异。

轮廓监控是近几年出现的SPC应用问题。轮廓是一条反映可测质量特性与不同维度变量关系的曲线。对由一系列轮廓曲线组成的时间序列数据进行监控被称为轮廓监控。Koh等[3]将轮廓曲线应用到锻造过程控制中。Walker等[4]用垂直密度轮廓曲线(verticaldensityprofiles,VDP)来描述木板质量，并尝试在历史轮廓中寻找异常点并建立模型。

异常点识别是第一阶段轮廓监控中的重要组成部分。异常点的存在容易造成分析错误，如以此为基础建立模型，将严重影响到第二阶段的判断。因此在进行第一阶段历史数据建模前，筛选并剔除异常点是有必要的。异常点识别的方法主要分为两类。第一类是参数方法，主要针对线性轮廓模型或者可以拟合成简单非线性组合的轮廓模型。一般的思路是将轮廓数据回归分析后的参数估计值视为多元变量，并用多元统计方法进行异常点识别。Tracy[5]将HotellingT2方法应用于多变量控制图中。Kang等[6]考虑参数间的相关性，对线性轮廓中参数估计值进行调整，然后用多EWMA控制图进行监控。第二类是非参数方法。Nagappan等[7]提出用基于轮廓残差建立的五尺度控制图法来实现复杂轮廓的监控。Zhang等[8]针对独立同分布且方差为正态分布的轮廓，提出χ2控制图方法与稳健χ2控制图方法。Chang等[9]用B样条来拟合非常规曲线以实现监控。Girimurugan等[10]采用小波分析的方法解决存在微小变化轮廓的异常点识别问题并取得不错的效果。

近年来，各种处理轮廓的方法相继出现，与此同时，一些问题也逐渐凸显出来。不同方法对轮廓有不同的要求，如维度要求、数据类型要求等。这些方法在准确性上的提升常依赖于对维度、数据类型这些条件的严格控制。为了弱化这种依赖关系，轮廓数据预处理思想逐渐成型，降维就是其中之一。Ding等[11]分别用主成分分析(PCA)和独立成分分析(ICA)的方法对轮廓数据进行降维处理，为先降维后分析的研究路线奠定了基础。Colosimo等[12]将先进行PCA降维的轮廓处理方法应用到机械组件圆周轮廓的轮廓监控中。Shiau等[13]也利用Ding的理论，结合HotellingT2方法对随机非线性的轮廓进行了分析。

结合了线性降维方法的非参数轮廓处理方法以其较大的灵活性这一特点，在轮廓分析领域得到了充分认可。但这种方法的应用范围远不及轮廓分析本身的应用范围，因此必须对方法适用性进行扩展。2000年后逐渐走向成熟的非线性降维就是一个扩展方向，Lee等[14]对非线性降维方法作了很好的总结，Neto等[15]曾尝试将结合了Laplacian方法的非参数分析方法应用于轮廓异常点分析问题中。

等距特征映射(isometricmapping,ISOMAP)2000年由Tenenbaum等[16]提出，提出后便得到了广泛重视并被接纳。这种基于数据点之间测地距离的非线性降维方法能够尽可能地保存流形中的相邻关系，从而实现全局降维。基于此，本文提出一种结合了ISOMAP非线性降维与χ2控制图方法的轮廓异常点识别方法，以实现复杂高维轮廓异常点的准确识别。仿真对比分析与真实数据识别结果将被用于判断本文所提方法的准确性。

1模型提出与假设

轮廓监控第一阶段的监控对象是已有的轮廓数据集。在此，我们假设有N条轮廓线，第i(i=1,2，…,N)条轮廓由M个点组成，每个点都表示特定条件xij下对应的质量特性yij的值。如果对于所有的i(i=1,2，…,N)，xij是一个固定值，则称此轮廓是平衡的，此时，我们可以把这组平衡的轮廓看作是一个N×M的矩阵。

已有的这些轮廓都是随机均匀抽样得到的样本，由于过程稳定性不可知，因此这些轮廓数据中可能存在异常点。

假设用于第一阶段的每条轮廓都是非参数的轮廓，即对于每条受控轮廓，都服从以下模型：

yij=f0(xij)+εijj=1,2,…,M;i∈S0

(1)

而对于其他异常点轮廓，则满足

yij=fi(xij)+εijj=1,2,…,M;i∈S1

(2)

模型中，εij是对于所有i、j都满足均值为0、方差为σ2独立同分布的随机误差项。集合S0、S1分别是受控轮廓集与异常轮廓集。所有受控的轮廓拟合的f0是某个确定的函数，而fi可以是不确定的，即异常点不同，fi可以不同。

针对非参数轮廓的第一阶段异常点识别问题，本文提出以下基本流程：首先，采用ISOMAP对历史轮廓数据进行降维；然后，对降维后的数据用χ2控制图进行分析，找出异常点。

1.1ISOMAP方法

ISOMAP是一种基于数据点之间测地距离的非线性降维方法，用以剥离出嵌入在高维空间中的低维子流形。低维流形中最近邻的点在高维空间中也是近邻的，由此，可以通过对高维空间中各点与近邻点路径距离进行分析来揭示低维流形的情况。具体步骤如下[16]：

(1)计算每个点的近邻点(K邻域或者ε邻域)。

(2)在样本集上定义一个赋权无向图。对于任意的点i，需要将i与其他所有点进行比较，若i与j互为近邻点(即j在i的K邻域或者ε邻域内)，则边的权值为i和j之间的欧氏距离，若i与j不为近邻点，则令距离为0。

(3)计算赋权无向图中两点之间的最短距离。采用下面的方法利用欧氏距离来逼近测地距离：首先，计算初始距离矩阵DG=(dG(i,j))，其中，当j为i的近邻点时，dG(i,j)=dX(i,j)，否则dG(i,j)=∞，这里dX(i,j)为i和j的欧氏距离，dG(i,j)为i和j的测地距离；然后，对于每一个k(k=1,2,…,N)，以min(dG(i,j),dG(i,k)+dG(k,j))代替初始的dG(i,j)，直到对于任意i与j，dG(i,j)不变时算法终止，即得到距离矩阵DG=(dG(i,j))。

(4)建立更低维的线性嵌入。应用经典的多维尺度分析(multidimensional scaling, MDS)方法得到d维欧氏空间的距离矩阵DY=(dY(i,j))，这个嵌入空间能够最大限度地保持流形的内在几何特征。新空间里的向量Yi需要使以下E函数最小：

E=‖τ(DG)-τ(DY)‖L2

(3)

定义τ(D)=-HSH/2，其中S为平方距离矩阵,S=D2，H为中心距离矩阵[17]。在进行ISOMAP降维的过程中用户需要自行设置相邻点参数K或者邻域半径参数ε(二者只需设定其一)，该项参数的设定直接影响到最后结果的准确性。Samko等[18]给出了ISOMAP中最佳参数K选择的方法，具体流程如下：

(1)参数可能存在区间的确定，即Kopt∈[Kmin,Kmax]。其中Kmin是能够使整个赋权无向图链接起来的K的最小值，Kmax是K的最大值，K的选择需满足以下条件：

(4)

式中，Q为边缘点的数量。选择εmax为max(dX(i,j))，dX(i,j)为ISOMAP的输入距离。

(2)对选定区间内的每一个整数值进行成本函数E(K)的计算。

(3)选出所有的极小值E(K)以及对应的K。

(4)用以下方法找到最终最合适的Kopt：

(5)

式中，ρDGDY为DG与DY的标准线性相关系数。

1.2χ2控制图

χ2控制图是一种非参数统计方法[8]，是可以不用对轮廓进行拟合而直接对轮廓数据进行统计分析的方法。

若均值μI和协方差矩阵ΣI均已知，则可以对每一条轮廓求统计量Δi：

(6)

一般情况下，历史数据中都会存在异常点，且μI和ΣI均未知，此时需要根据已有的轮廓数据，通过统计方法得到未知参数的近似值，再代入式(6)后判断轮廓是否为异常点。

Zhang等[8]将χ2控制图用于历史数据的处理，采用估计方法得到μI和ΣI的估计值，然后代入式(6)，依次确定每条轮廓是否为异常点。该估计方法如下：

(7)

(8)

(9)

式(8)中的方差估计在轮廓方差相等或接近时偏差很小。但是之前ISOMAP降维后的数据将很难保持等方差性，因此Zhang等[8]提出了更加稳健的方差估计方法：

(10)

对于方差特征不同的数据，应该采用不同的估计方法，因此在异常点识别前必须对轮廓数据进行齐方差性检验，方差比较接近时采用式(8)、式(9)给出的估计方法，而在方差不齐时使用式(10)给出的估计方法。

2性能测试

2.1仿真数据分析

我们采用第一类错误发生率和第二类错误发生率来对判定结果进行评价。第一类错误发生率是将正常点判定为异常点的点的数量与所有正常点数量的比值，记为eⅠ；第二类错误发生率是将异常点判定为正常点的点的数量与所有异常点数量的比值，记为eⅡ。具体计算方法如下：

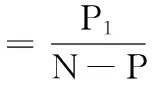
(11)

(12)

式中，P为仿真过程中设定的异常点数量；P1为错判的正常点数量；P2为错判的异常点的数量。

本文利用MATLAB软件进行仿真实验。首先生成随机的轮廓(包含正常轮廓与异常轮廓)，然后采用本文提出的先ISOMAP降维、后非线性异常点识别的方法对模拟的数据进行异常点识别，用两类错误发生率来评价方法的实用性和有效性。

每次仿真实验都产生一个存在异常轮廓的轮廓数据集，即生成一个存在异常行的N×M矩阵，结合提出的方法，比较检验出的异常点与设置的异常点之间的位置差异。

为了尽可能接近一个非参数轮廓，我们采用以下函数来产生轮廓内的质量特征向量：

(13)

式(13)中，变量有两个：一个是参数a，另一个是满足正态分布N(0,σ2)随机变量ε的方差σ2。假设受控状态下，a为0.8，s2为1。每个轮廓中，变量x从0.02开始以0.02为步长，均匀取800个点，由此800个点形成一个轮廓，图1展示了该轮廓的基本形状，图中两条轮廓的a值分别为0.8和1.1，a=0.8即受控状态下的轮廓。

图1　仿真数据形成的轮廓形状图

仿真中共随机生成200个轮廓，包括200×p条异常轮廓，其中p为异常比例。用所述方法仿真1000次后，将统计出的第一类错误和第二类错误出现的频率与Zhang等[8]的方法进行对比。在检验中，置信区间1-α设定为0.9。

根据上述参数选择方法，首先选择参数K可能存在的区间。为了能够产生赋权无向图且不至于造成过大的运算成本，暂定区间[3,10]为目标区间。通过计算降维前后数据相关程度，最终确定参数K为10。

在进行异常值非参数统计检验前，需要最终确定数据降维后的维度。根据Samko等[18]的说明，降维后残差方差(residual variance, RV)的变化是一个重要的依据。图2展示了维度由1到10变化对应的降维后的残差方差VR变化(所有残差变化均已作归一化处理)情况。从图2中可以看出，降维过程中残差随着维度的增大而逐渐变小，说明降维维度不宜过小，维度4是曲线拐点。Tenenbaum等[16]提出，最佳维度应选择降维残差曲线的拐点，故4可以作为最终的降维维度。

图2　VR与etotal随降维维度D变化图

但是降维维度的最优选取点并不等同于最终ISOMAP与χ2最优维度的选择。为验证维度4选择的正确性，图2还展示了总错误比率etotal(etotal=eⅠ+eⅡ)随降维维度变化的关系。可以看出，随着维度值逐渐增大，etotal逐渐增大，说明维度取值不宜过大。图中实线反映归一化处理后残差方差VR相对变化与归一化处理后总错误率etotal相对变化总的变化情况，可以看出，曲线两端高中间低，最低点对应的降维维度是4。按相同比重考虑降维残差和错误率的重要性，最终得到总相对变化的最低点即为最优维度选择点，故维度可选择为4。

图3和图4分别展示的是本文所提的ISOMAP结合χ2控制图的异常点识别方法与现有的χ2控制图异常点识别方法的结果对比，图3是eⅠ的结果对比，图4是eⅡ的结果对比，图中，实线是本文提出的方法的结果，虚线是Zhang等[8]所提出的单纯用χ2控制图得到的结果。

图3　eI随参数a变化图

图4　eⅡ随参数a变化图

从图3、图4中可以直观看出，随着参数a的变化，本文所提方法的第一类错误的发生率eⅠ均明显小于对比方法的eⅠ；在参数a小于0.85时，本文所提方法的第二类错误的发生率eⅡ小于对比方法的eⅡ，之后本文方法的优越性并不显著。随着异常比例p的提高，两种方法的性能逐渐接近。综合分析，在变化幅度较小的情况下，本文方法既能更加敏感地识别异常点，又能避免对稳定过程的误判。因此，所提出的方法适用于对小幅度异常点的识别，在降低第一类错误发生率的同时保证第二类错误发生率的稳定。

2.2案例数据分析

本文采用Walker等[4]的木板垂直密度轮廓组数据(简称VDP数据)，运用所提出的方法进行轮廓异常点识别。VDP数据是在木板生产过程中随机抽选样本，对每个木板样本不同位置的密度进行精确测量得到不同的质量轮廓曲线。这组轮廓中共有24条轮廓，每条轮廓内有314个点。

图5是残差与降维维度关系图，依据Tenenbaum等[16]的“拐点”理论，维度2是应选取的降维维度。为验证此结果，在具体操作中，多次使用ISOMAP方法分别将原数据降维至1～10维，并保留所有数据，分别进行χ2异常点判断，汇总后得到的结果如表1所示。由表1看出，降维维度2之后，重复率高的异常轮廓是轮廓6和轮廓10。

图5　ISOMAP降维中VR与降维维度D关系图

降维维度12345异常轮廓3,66,106,106,106,10降维维度678910异常轮廓6,102,6,10,212,6,103,6,104,6

如图6所示，轮廓10随着测量位置的变化，其VDP数据值始终低于总体水平，轮廓6在测量位置50～250区间内VDP数据值明显低于对应点总体水平，但在两端位置高于对应点总体水平。因此，这两条轮廓均表现出较为明显的差异，故该两条轮廓属于异常轮廓。由此说明本文方法能够以合理的降维维度取值有效地识别出异常点的位置。表1与图6的结果是对应的。

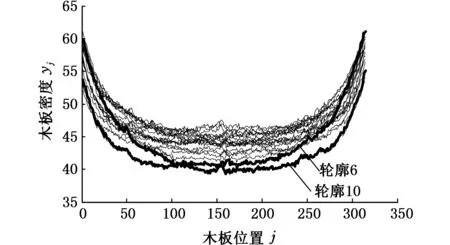
图6　由ISOMAP与χ2结合方法识别的异常点

图7展示的是由单纯χ2方法识别的异常点，轮廓9和轮廓14在形状上并无明显异常，是否是真异常点还值得考究。3号轮廓虽整体位于较高位置，但与相邻轮廓连接紧密，是否异常也还需要作更细致的统计研究。

图7　由χ2方法识别的异常点

3结论与展望

本文提出了ISOMAP降维结合χ2控制图的轮廓异常点识别方法。该方法通过引入ISOMAP降维方法成功解决了数据点多、维度爆炸的轮廓识别问题，能有效提取轮廓控制图的特征信息；使用χ2控制图解决了轮廓异常点识别问题。从随机轮廓仿真实验和VDP数据案例中不难看出,结合了ISOMAP的χ2控制图的轮廓异常点识别方法能准确识别异常点并保持较低的错误发生率。虽然本文在分析方法性能时并没有对数据类型、数据维度作明确要求，但所提方法依然表现出突出的异常点识别能力，因此结合了ISOMAP的χ2控制图轮廓异常点识别方法具有很强的适应性和应用前景。

所提出的方法中降维维度的选择十分关键，本文所提出的维度选择方法主要基于已知函数轮廓，但对于不同形状轮廓的适用性仍有待研究。

参考文献：

[1]WoodallWH,SpitznerDJ,MontgomeryDC,etal.UsingControlChartstoMonitorProcessandProductQualityProfiles[J].JournalofQualityTechnology, 2004, 36(3): 309-320.

[2]HawkinsDM,PeihuaQ,ChangWK.TheChangepointModelforStatisticalProcessControl[J].JournalofQualityTechnology, 2003, 35(4): 355-366.

[3]KohCKH,ShiJ,BlackJM,etal.TonnageSignatureAttributeAnalysisforStampingProcess[J].Transactions—NorthAmericanManufacturingResearchInstitutionofSME, 1996, 24: 193-198.

[4]WalkerE,WrightSP.ComparingCurvesUsingAdditiveModels[J].JournalofQualityTechnology, 2002, 34(1): 118-129.

[5]TracyND.MultivariateControlChartsforIndividualObservations[J].JournalofQualityTechnology, 1992, 24(2): 88-95.

[6]KangL,AlbinS.On-lineMonitoringWhentheProcessYieldsaLinearProfile[J].JournalofQualityTechnology, 2000, 32(4): 418-426.

[7]NagappanN,WilliamsL,VoukM,etal.UsingIn-processTestingMetricstoEstimatePost-releaseFieldQuality[C]//ISSRE’07.The18thIEEEInternationalSymposiumonSoftwareReliability, 2007.Trollhattan:IEEE, 2007: 209-214.

[8]ZhangH,AlbinS.DetectingOutliersinComplexProfilesUsingaχ2ControlChartMethod[J].IIETransactions, 2009, 41(4): 335-345.

[9]ChangSI,YadamaS.StatisticalProcessControlforMonitoringNon-linearProfilesUsingWaveletFilteringandB-splineApproximation[J].InternationalJournalofProductionResearch, 2010, 48(4): 1049-1068.

[10]GirimuruganS,ChickenE,PignatielloJrJJ,etal.WaveletAnovaforDetectionofLocalandGlobalProfileChanges[C]//Proceedingsofthe2013IndustrialandSystemsEngineeringResearchConference.SanJuan,PuertoRico:IIE. 2013: 3235-3244.

[11]DingY,ZengL,ZhouS.PhaseIAnalysisforMonitoringNonlinearProfilesinManufacturingProcesses[J].JournalofQualityTechnology, 2006, 38(3): 199-216.

[12]ColosimoBM,PacellaM.OntheUseofPrincipalComponentAnalysistoIdentifySystematicPatternsinRoundnessProfiles[J].QualityandReliabilityEngineeringInternational, 2007, 23(6): 707-725.

[13]ShiauJJH,HuangHL,LinSH,etal.MonitoringNonlinearProfileswithRandomEffectsbyNonparametricRegression[J].CommunicationsinStatistics—TheoryandMethods, 2009, 38(10): 1664-1679.

[14]LeeJA,VerleysenM.NonlinearDimensionalityReduction[M].NewYork:SpringerScience&BusinessMedia, 2007.

[15]NetoFM,deMagalhãesMS.ALaplacianSpectralMethodinPhaseIAnalysisofProfiles[J].AppliedStochasticModelsinBusinessandIndustry, 2012, 28(3): 251-263.

[16]TenenbaumJB,deSilvaV,LangfordJC.AGlobalGeometricFrameworkforNonlinearDimensionalityReduction[J].Science, 2000, 290(5500): 2319-2323.

[17]MardiaKV,KentJT,BibbyJM.MultivariateAnalysis[M].London:AcademicPress, 1979.

[18]SamkoO,MarshallAD,RosinPL.SelectionoftheOptimalParameterValuefortheIsomapAlgorithm[J].PatternRecognitionLetters, 2006, 27(9): 968-979.

(编辑苏卫国)

收稿日期：2015-06-30

中图分类号：TH165.4

DOI：10.3969/j.issn.1004-132X.2016.12.008

作者简介：聂斌，男，1971年生。天津大学管理与经济学部工业工程系副教授、硕士研究生导师。主要研究方向为统计过程控制、可靠性工程等。李京亚，女，1990年生。天津大学管理与经济学部硕士研究生。姚雪海，男，1989年生。天津大学管理与经济学部硕士研究生。

DetectingOutliersinComplexProfileswithISOMAP

NieBinLiJingyaYaoXuehai

TianjinUniversity,Tianjin, 300072

Abstract:Researches of outlier-detection methods for the high-dimensional complex profiles are as an important branch of profile monitoring. Considering the complexity of some high-dimensional profiles, a matrix model for non-parametric profile was set up. Based on this model, a combined method was proposed, where ISOMAP could reduce the dimensionality based on geodesic distance and χ2 control chart could identify profile outliers. The proposed method shows good performance in the accuracy of outlier detection by both simulation studies and real case studies.

Key words:outlier detection; isometric mapping(ISOMAP); profile; dimension-deduction