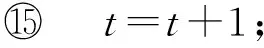基于泛化反向学习的多目标约束差分进化算法

魏文红　王甲海　陶　铭　袁华强

1(东莞理工学院计算机学院　广东东莞　523808)2(中山大学计算机科学系　广州　510006) (weiwh@dgut.edu.cn)



基于泛化反向学习的多目标约束差分进化算法

魏文红1王甲海2陶铭1袁华强1

1(东莞理工学院计算机学院广东东莞523808)2(中山大学计算机科学系广州510006) (weiwh@dgut.edu.cn)

摘要差分进化算法是一种简单有效的进化算法，基于泛化反向学习的机制在进化算法中经常可以引导种群的进化.针对多目标的约束优化问题，提出了一种基于泛化反向学习的多目标约束差分进化算法.该算法采用基于泛化反向学习的机制(generalized opposition-based learning, GOBL)产生变换种群，然后在种群初始化和代跳跃阶段，利用非支配排序、拥挤距离和约束处理技术从原始种群和其变换种群中选择更优的种群个体作为新的种群继续迭代进化；该算法通过采用基于泛化反向学习的机制，可以引导种群个体慢慢向最优的Pareto前沿逼近，以求得最优解集.最后采用多目标Benchmark问题对该算法进行了实验评估，实验结果表明：与NSGA-Ⅱ，MOEAD及其他的多目标进化算法相比，提出的算法具有更好的收敛性，并且产生的解能够逼近最优的Pareto前沿.

关键词差分进化；泛化反向学习；多目标优化；约束优化;非支配排序

多目标优化问题(multi-objective optimization problems, MOPs)在许多领域都有广泛的应用，特别是科学、工程和经济领域[1].与单目标优化问题不同，多目标优化问题必须同时优化多个目标函数.由于多个目标函数相互冲突，所以不能像求解单目标优化问题一样，总能找到一个最优或近优解，而是求解到一个满足所有目标函数折中的解集，这个解集称之为Pareto最优解[2].由于现实中的科学和工程问题都存在着各种各样的约束条件，因此多目标约束优化问题(multi-objective constrained optimization problems, MCOPs)引起了研究者们的关注[3-5].因为约束条件的出现，会导致可行解区域减小并使得搜索解的过程变得更为复杂，因此如何采用约束处理机制来处理MCOPs，将是一个值得研究的课题.

进化算法(evolution algorithm， EA)是一种随机的、基于种群的优化算法，它在每一次运行中可以找到多个最优解，天生具有解决MOPs的特性.在过去的几十年中，提出了大量的多目标进化算法[3-8]，典型的代表主要有：Deb等人[3]提出的快速和精英选择的多目标非支配排序遗传算法(nondominated sorting genetic algorithm， NSGA-Ⅱ)和Zhang等人[8]提出的基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decom-position， MOEAD).

差分进化算法(differential evolution， DE)是由Storn和Price[9]首次提出的，它是一种功能强大、结构简单、易用且鲁棒性强的全局优化算法，该算法在解决单目标约束优化问题(COPs)时已经取得了显著的成就.Abbass等人[10]首次将DE算法用来解决MOPs，称为Pareto前沿差分进化算法(Pareto-frontier differ-ential evolution， PDE).在PDE算法中，通过DE产生子代，然后子代与父代通过支配关系进行比较，丢弃支配解，只保留非支配解到下一代中.Madavan[11]提出了Pareto差分进化方法(Pareto differential evolution approach, PDEA)，该算法与PDE类似，通过DE产生子代，然后合并父代与子代个体，再计算它们的Pareto非支配排序和多样性排序，最后根据排序选择保留最优个体.Xue等人[12]提出了多目标差分进化算法(multi-objective differential evolution, MODE)，该算法与NSGA-Ⅱ类似，也采用了Pareto非支配排序和拥挤距离排序技术，不同的是，MODE的适应值首先通过Pareto非支配排序计算，然后根据拥挤距离值改变.Robic等人[13]提出了多目标优化差分进化算法(differential evolution for multi-objective optimization, DEMO)，该算法与MODE有点相似，仍然采用了Pareto非支配排序和拥挤距离排序技术，但是它又像PDEA一样，把父代和子代合并，再计算它们的Pareto非支配排序和拥挤距离排序，以提升候选解的均匀分布.

基于反向学习(opposition-based learning， OBL)的机制是由Al-Qunaieer等人[14]首次提出的，该方法为了获得更优的解来进行下一次迭代，在每次迭代过程中，不仅要评价本次搜索到的最优解，而且还要评价与该最优解处于相反方向的解，然后得出最终的最优解，用来进行下一次迭代.最近基于反向学习的机器学习方法被广泛用于一些启发式进化算法如差分进化、粒子群、人工神经网络、蚁群和人工蜜蜂算法等[15-16].根据基于反向学习的原理，Wang等人[17]提出了一种基于泛化反向学习(generalized opposition-based learning, GOBL)的机制，GOBL采用转换搜索空间技术把当前空间的解转换到一个新的空间去，即在求解过程中，不但要考虑当前空间的候选解，而且还要考虑转换空间的候选解.由于同时搜索当前空间和转换空间的解，GOBL能够很快地发现最优解.

Rahnamayan等人[18]首次提出了基于反向学习的差分进化算法，在该算法中，采用基于反向学习的机制来初始化种群.之后的几年里，包括Rahnamayan在内的许多专家学者，分别提出了改进的基于反向学习的差分进化算法[19-23].后来OBL机制也被用于解决多目标优化问题，Peng等人[24]提出了一种解决多目标优化问题的基于反向学习的多目标差分进化算法(opposition-based multi-objective differential evolution algorithm，OMODE)，该算法采用OBL机制产生初始种群的反向种群，然后通过Pareto非支配排序和拥挤距离排序从原初始种群和其反向种群中选最优个体组成新的初始种群继续迭代.Dong等人[25]提出了一种基于反向操作的多目标差分进化算法(multi-objective differential evolution based on opposite operation, MDEOO)，与OMODE不同的是，该算法不但在种群初始化阶段产生反向种群，而且在子代的迭代过程中也产生子代的反向种群，然后仍然采用Pareto非支配排序和拥挤距离排序技术从原始种群和其反向种群中选择最优的个体继续迭代.

最近Wang等人[22]采用GOBL机制，提出了一种基于泛化反向学习的差分进化算法(generalized opposition-based differential evolution, GODE)，该算法被证明具有较快的收敛速度和求解精度.然而该算法却不能用于解决多目标优化问题，更不能解决多目标约束优化问题.另外包括OMODE和MDEOO在内的基于反向学习的多目标差分进化算法也不能解决多目标约束优化问题.在这种背景下，本文提出了一种基于泛化反向学习的多目标约束差分进化算法(generalized opposition-based multi-objective constrained differential evolution, GOMCDE)，并且针对多目标测试函数集进行了实验测试.测试结果显示，与NSGA-Ⅱ和MOEAD及其他相关算法相比，GOMCDE算法具有更强的全局搜索性能、更快的收敛速度和更好的Pareto前沿.

1相关背景知识

1.1多目标约束优化问题

在多目标约束优化问题中，既存在等式约束条件和不等式约束条件，还包括向量x的上界和下界，具体如下：

(1)

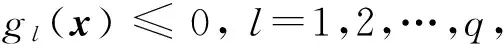
(2)

(3)

(4)

其中,f(x)为k个目标函数，需要同时优化；x=(x1,x2,…,xn)为n维决策向量；gj(x) ≤ 0和hj(x)=0分别表示q个不等式约束和m-q个等式约束；函数fk，gl和hl为线性或非线性实数函数；upj和lowj分别为变量xj的上界和下界.另外，假定可行解空间中满足所有约束的点集合用U表示，搜索空间中满足上界和下界约束的点集合用S表示，其中S⊂U.

为了考虑多个目标之间的平衡，引入了解之间的支配概念.假定解向量x=(x1,x2,…,xn)，y=(y1,y2,…,yn)，如果xi≤yi,i=1,2,…,n且x≠y,则xy，即称为x支配y.如果对于一个解向量满足∃x∈U,xx*，则称∃x∈U,xx*为Pareto最优解.由所有Pareto最优解组成的集合，称为Pareto最优解集(Pareto set， PS).在多目标优化问题中，Pareto最优解集在目标空间对应的目标向量称为Pareto前沿(Pareto front， PF)，具体表示如下：

(5)

求解多目标约束优化问题的目标，就是要找到一个满足各种约束条件的Pareto前沿.

1.2差分进化算法

差分进化算法是一类比较流行的进化算法，并且具有良好的性能，广泛地应用于各种应用领域.在差分进化算法中，一般包括NP个种群，每个个体向量的维度为n.一般地，个体表示为：向量xi,t=(x1i,t,x2i,t,…,xni,t)，其中i=1,2,…,NP，NP为种群大小，n为个体向量的维度，t为当前种群的代数.差分进化算法包括3个主要的操作：变异、交叉和选择[13].

1) 变异.在变异操作中，对于每个种群产生目标向量vi,t，变异策略主要如下：

(6)

(7)

(8)

(9)

(10)

其中，下标r1，r2，r3，r4，r5都是随机从集合{1,2,…,NP}{i}中选取的；xbest,t为种群在第t代最好的个体；缩放因子F为实数，F∈[0,1].

2) 交叉.交叉操作主要产生试验变量ui,t=(u1i,t,u2i,t,…,uni,t)，具体如下：

(11)

其中，i=1,2,…,NP,j=1,2,…,n；jrandom是属于1～n之间的一个随机整数；randomj(0,1)为对于每个j产生[0,1]均匀分布的随机数；使用参数jrandom是为了保证试验向量ui,t不同于目标向量xi,t；交叉概率因子CR的取值通常为0～1.

3) 选择.在选择操作中，目标向量xi,t和试验向量ui,t根据它们的适应值进行比较，选择适应值更优的进入下一代种群：

(12)

1.3反向学习

Fig. 1　An example for opposite point.图1　反向点的例子

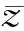
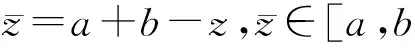
(13)

如果对于一个n维向量的反向点，则用如下定义表示.

定义2. 假设P=(z1,z2,…,zn)为一个n维空间的点，其中z1,z2,…,zn∈且zi∈[ai,bi]，∀i∈{1,2,…,n}，则P的反向点由式(14)决定.

(14)

有了反向点的定义之后，那么基于反向学习的优化可以定义如下:

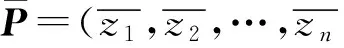
1.4泛化反向学习

OBL仅仅是求反向点，而GOBL则是把当前空间的点或候选解变换到一个新的空间，然后和OBL原理一样，同时评价当前空间和变换空间的候选解，选出最优的候选解.在文献[17]中，GOBL被证明具有更强的能力发现全局最优解.

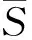
(15)

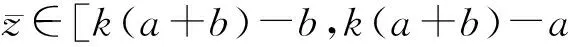
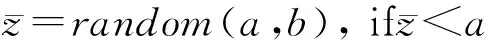
(16)

其中,random(a,b)为产生[a,b]中的随机数.

定义5. 假设P=(z1,z2,…,zn)为一个n维空间的点，其中z1,z2,…,zn∈且zi∈[ai,bi]，∀i∈{1,2,…,n}.则P的转换空间点的元素可由式(17)计算.

(17)

其中,k=random(0,1).

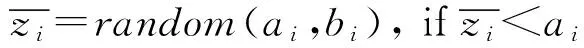
(18)

2GOMCDE算法

根据GOBL定义可知，基于泛化反向学习的机制需要比较种群与转换种群的适应值.而对于多目标约束优化问题的适应值比较不能像单目标无约束优化问题一样简单处理.本文采用适应值变换、Pareto非支配排序和拥挤距离排序技术来处理GOBL中的适应值比较问题.

2.1适应值变换约束处理技术

为了解决多目标约束优化问题，我们必须在GOMCDE算法中加入约束处理技术.我们知道，在无约束的差分进化算法中，适应值都等于目标函数值，但是在约束差分进化算法中，由于约束的存在，不能简单地考虑适应值等于目标函数值，必须要考虑约束条件的存在.比如，对于最小值优化问题，解向量x的目标函数值比y小，但x却违反了约束条件而y没有违反约束条件.此时，应该考虑可能解向量y比x更优.基于这种原理，我们采用了适应值变换技术来处理约束优化问题.

一般地，对于约束优化问题，经常会把等式约束转化成不等式约束，具体如下：

(19)

其中,l∈{q+1,q+2,… ,m}；δ为等式约束违反的容忍因子，一般取正整数.解x到第l个约束的距离可以表示为

(20)

那么解x到可行解区域的边界距离，即约束违反程度可以表示为

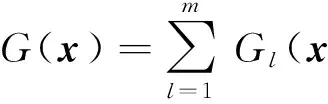
(21)

在适应值变换约束处理技术中，为了更好地处理约束差分进化算法中的适应值，采用应值变换方法把种群分成3种状态：不可行状态、半可行状态和可行状态.

1) 不可行状态.在不可行状态下，种群只包含了不可行解，因此不用考虑目标函数值，只需要考虑约束违反程度.约束违反程度可以通过式(21)计算，此时适应值计算式为

(22)

2) 半可行状态.在半可行状态下，种群既包含了部分可行解又包含了部分不可行解，因此就必须在目标函数值和约束违反程度之间找到一个平衡点.从解的层面分析，此时把种群细分为可行解组(Z1)和不可行解组(Z2).因此解xi,t的目标函数值f′(xi,t)就可以转换成：

(23)

其中,φ是上一代种群的可行解比率；xbest,t和xworst,t分别是可行解组Z1最优和最差的解.进一步把式(23)归一化为

(24)

式(20)可以计算约束违反程度，在此状态下，式(21)归一化为

(25)

因此最终的适应值可以表示为

(26)

3) 可行状态.在可行状态下，种群中所有个体都是可行解，因此就可以看作是无约束优化问题来处理.此时适应值就等于目标函数值f(xi,t)，具体为

(27)

通过适应值变换技术，所有的个体都基于变换后的适应值进行比较，选择适应值更优的个体继续进化.对于多目标约束优化问题，种群中的个体采用Pareto非支配排序技术进行比较.从适应值变换的原理可以看出，对于多目标无约束优化问题，适应值变换技术同样适用，即无约束优化问题中的种群个体属于适应值变换中的第3种状态：可行状态.

2.2Pareto非支配排序

在Pareto非支配排序之前，必须先计算：1)支配数np，它是解p支配其他解的个数；2)支配集Sp.在Pareto非支配排序过程中，首先从支配集Sp中选取所有np=0的成员q加入链表Q中，然后设置其他成员的支配数减1，重复这2步直到所有的成员都加入到链表Q中为止.

2.3拥挤距离

拥挤距离用来衡量解分布的密度，在非支配集I中，解i的拥挤距离等于解i的邻居解i-1和解i+1之间沿着每个目标的平均距离，具体可根据式(28)计算.在计算拥挤距离时，首先要根据目标函数值排序种群.在本文中，由于约束的存在，我们根据变换后的适应值来排序种群，然后再根据式(28)计算每个解的拥挤距离.由于式(28)并不能应用于边界解的拥挤距离的计算，所以边界解的拥挤距离通常被设置为无穷大.

I[i]distance=(I[i+1].m-I[i-1].m)

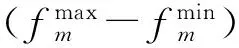
(28)

2.4算法描述

绝大多数的进化算法都是在种群初始化阶段和代跳跃阶段使用OBL机制求其反向种群.在本文中，我们也在种群初始化阶段和代跳跃阶段使用GOBL机制求其变换种群.对于随机生成的初始种群P0(其中种群大小为NP，个体向量的维度为n)，通过式GOPji,0=k(aj+bj)-Pji,0计算出其变换种群GOP0.其中，i=1,2,…,NP；j=1,2,…,n；k为[0,1]之间的随时数.然后采用Pareto非支配排序和拥挤距离排序技术根据变换后的适应值，从种群P0和GOP0中选出NP个适应值更优的个体组成新的初始种群P0.在种群代跳跃阶段，与单目标优化问题相同的是，该阶段的执行也必须满足一个代跳跃概率J，在绝大部分情况下J=0.3[18].与单目标优化问题不同的是，变换种群的计算式与种群初始化阶段类似，仍然采用[a,b]作为决策空间.即GOPji,t=k(aj+bj)-Pji,t，其中t为种群的代数.最后在个体的生成选择阶段，与其他多目标差分进化算法的流程一样，采用Pareto非支配排序和拥挤距离排序技术根据变换后的适应值，从父代群Pt-1、子代种群Pt和变换种群GOP中选出NP个适应值更优的个体继续迭代.GOMCDE算法伪代码如下：

算法1. GOMCDE伪代码.

输入：初始种群P0=(x1,0,x2,0,…,xNP,0);

输出：外部非支配集E中的个体.

① 评价种群P0,求出变换后的适应值和约束违反程度;

② for (i=0;i

③ for (j=0;j

④GOPji,0=k×(aj+bj)-Pji,0;

⑤ ifGOPji,0bj

⑥GOPji,0=random(aj,bj);

⑦ end if

⑧ end for

⑨ end for

⑩ 评价变换种群GOP0,求出变换后的适应值和约束违反程度;

从算法1的描述中可以看出，GOMCDE算法简单且容易操作，它采用适应值变换技术不但可以解决多目标约束优化问题，同时也适用于多目标无约束优化问题.由于GOBL的时间复杂度为O(NP×n)，Pareto非支配排序的时间复杂度为O(k×NP×NP)，拥挤距离排序的时间复杂度为O(k×NP×logNP)，所以GOMCDE算法的时间复杂度为O(NP×(n+k×NP)).

3实验测试

为了进一步验证GOMCDE算法的有效性，我们对GOMCDE算法和NSGA-Ⅱ[3]，EAMO[26]，CHMEO[5]，CMODE[6]，CMOPSO[27]等算法针对多目标约束优化问题进行了对比实验测试.用于测试的约束优化问题主要包括BNN[28]，SRN[29]，TNK[30]，CONSTR[31]，CTP1-CTP7[31]，Welded Beam Problem[26]，其中Welded Beam Problem是一个现实生活中的测试问题.在这些测试问题中，有些具有连续的Pareto前沿，有些则是不连续的.为了证明GOMCDE算法对于多目标无约束优化问题同样有效，我们对GOMCDE算法和NSGA-Ⅱ[3]，MOEAD[8]，MODE-RMO[32]，OMODE[24]，MDEOO[25]等算法针对ZDT1-ZDT4[33]和ZDT6[33]等无约束优化问题进行了对比实验测试.在所有的实验过程中，实验环境为64位的Windows 7系统，其中CPU为Intel Core TM 2.83 GHz，内存为4 GB，编程语言为Maltab 2013 b.

3.1实验参数设置

1) 种群大小.NP=100.

2) 交叉概率.CR=0.8.

3) 缩放因子.F=0.2.

4) 代跳跃概率.J=0.3.

5) 最大代数.Gmax=100.

3.2性能评价指标

1) Pareto前沿PF[3].Pareto非支配集中的最优解映射在目标空间中的目标向量.

2) 收敛性评价指标r[3].表示近似解到Pareto前沿最优解的欧氏距离，r值越小，表示近似解越接近Pareto前沿，收敛性越好.r的计算公式为

(29)

其中,N为非支配解的个数，di为相邻非支配解之间的欧氏距离.

3) 多样性评价指标Δ[3].表示近似解集的分散程度，Δ值越小，表示解集的分布性越好，即多样性就越好.当Δ=0时，说明所有的解沿着Pareto前沿均匀分布.Δ的计算公式为

(30)

4) 超体积评价指标IH(hypervolume indicator)[34].表示近似解集A在目标空间相对于参考点所支配的空间大小，IH值越大，解集A在目标空间所支配的区域就越大，即该解集A就越接近最优解，分布性越好，同时也可以表示收敛性越好.

6) 基于ε支配的评价指标Iε[34].对于给定的ε>0和参考集R，Iε可以定义为

(31)

其中,A和B为2个近似解集.Iε值越小，表示算法的收敛性越好.

7) Mann-Whitney检验分析[35].该检验分析是由Mann和Whitney提出的针对2个独立样本进行分析的非参数检测方法，它在这2独立样本的总体分布未知的情况下，通过2组样本的分析来推断总体的分布是否存在显著差异.

3.3性能评价指标

实验中所有算法对于每一个测试函数都运行50次，在每一次运行过程中设置Max_FEs=2.5×104.

1) 针对约束优化问题的比较

Table 1　Mann-Whitney Analysis onandIεBetween GOMCDE and Other Algorithms

Fig. 2　Pareto front on CTP1 for six algorithms.图2　6种算法针对CTP1测试问题的Pareto前沿

我们随机地选取了CTP1测试问题做了Pareto前沿的测试，图2显示了这6种算法的Pareto前沿测试结果，NSGA-Ⅱ算法虽然能够逼近最优Pareto前沿，但其解的分布性较差；EAMO算法的分布性较优于NSGA-Ⅱ算法，但是它的收敛性稍差;CMODE算法与EAMO算法类似;CHMEO，CMOPSO算法在收敛性和分布性方面都明显优于前面3种算法，但是当它们与GOMCDE算法比较时，却又不及GOMCDE算法.所以GOMCDE算法不但具有较好的收敛性，而且还具有比较均匀的分布性，明显优于其他5种算法.

Fig.s.图3　6种算法针对CTP4测试问题关于和Iε的统计盒图

2) 针对无约束优化问题比较

因为GOMCDE算法也可以适用于无约束优化问题，所以我们也对GOMCDE算法与NSGA-Ⅱ，MOEAD，MODE-RMO以及其他2类基于OBL机制的多目标算法OMODE，MDEOO针对无约束的Benchmark问题进行了实验测试，表2显示了比较结果，其中粗体表示该算法的值最优，旁边括号表示这6种算法的排名.

Table 2　Convergence and Diversity Comparison Between GOMCDE and Other Algorithms

从表2可以看到，GOMCDE算法明显优于其他算法，绝大部分结果都排在第一的位置；而且OMODE，MDEOO算法比NSGA-Ⅱ，MOEAD，MODE-RMO算法也略占优势，这是由于OMODE和MDEOO算法都采用了OBL机制的原因.另外还可以看出，MDEOO算法比OMODE算法稍占优势，这是因为虽然它们都采用了OBL机制，但OMODE算法只是在种群初始化阶段采用OBL机制，而MDEOO算法在种群初始化和代跳跃阶段都采用了OBL机制.GOMCDE算法比MDEOO算法较优是因为GOMCDE算法在种群初始化和代跳跃阶段采用了GOBL机制.

对于无约束优化问题，我们随机地选取了ZDT2测试问题做了Pareto前沿的测试，图4显示了这6种算法的Pareto前沿测试结果.从测试结果来看，GOMCDE算法和OMODE算法、MDEOO算法虽然都达到了最优Pareto前沿，但是GOMCDE算法在分布性方面明显要优于OMODE算法和MDEOO算法；NSGA-Ⅱ，MOEAD，MODE-RMO算法无论是在收敛性还是分布性方面均稍弱于OMODE算法和MDEOO算法，更弱于GOMCDE算法.

Fig. 4　Pareto front on ZDT2 for six algorithms.图4　6种算法针对ZDT2测试问题的Pareto前沿

4结束语

GOBL是一种泛化的OBL机制，把GOBL机制应用于进化算法被证明能够加快算法的收敛速度和提高算法的求解精度.然而GOBL机制却从来没有应用于多目标优化问题中，更没有用来解决多目标约束优化问题.针对此情况，本文结合GOBL机制，提出了GOMCDE算法.该算法首先利用GOBL机制生成变换种群；然后采用Pareto非支配排序、拥挤距离排序和约束处理技术从初始种群和其变换种群中选取最优的个体组成新的初始种群继续迭代；最后为了加速收敛速度，采用GOBL机制代跳跃方法产生子代种群的变换种群，再次使用Pareto非支配排序、拥挤距离排序和约束处理技术从父代种群、子代种群及其变换种群中选择最优的个体组成新的子代种群继续迭代.为了验证本文算法的优势，针对多目标测试函数集进行了实验测试.测试结果表明，与其他相关算法相比，GOMCDE算法具有更强的全局搜索性能、更快的收敛速度和更好的Pareto前沿.

参考文献

[1]Zhou A, Qu B, Li H. Multiobjective evolutionary algorithms: A survey of the state of the art[J]. Swarm and Evolutionary Computation, 2011, 1(1): 32-49

[2]He Z, Yen G, Zhang J. Fuzzy-based Pareto optimality for many-objective evolutionary algorithms[J]. IEEE Trans on Evolutionary Computation, 2014, 18(2): 269-285

[3]Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Trans on Evolutionary Computation, 2002, 6(2): 182-197

[4]Yen G G, Leong W F. A multiobjective particle swarm optimizer for constrained optimization[J]. Recent Algorithms and Applications in Swarm Intelligence Research, 2011, 2(1): 1-23

[5]Woldesenbet G, Yen G, Tessema G. Constraint handling in multiobjective evolutionary optimization[J]. IEEE Trans on Evolutionary Computation, 2009, 13(3): 514-525

[6]Qu B, Suganthan P N. Constrained multi-objective optimization algorithm with an ensemble of constraint handling methods[J]. Engineering Optimization, 2011, 43(4): 403-416

[7]Zheng Jinhua, Liu Lei, Li Miqing, et al. Difference selection strategy for solving complex multi-objective problems[J]. Journal of Computer Research and Development, 2015, 52(9): 2123-2134 (in Chinese)(郑金华, 刘磊, 李密青, 等. 差分选择策略在复杂多目标优化问题中的研究[J]. 计算机研究与发展, 2015, 52(9): 2123-2134)

[8]Zhang Q, Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition[J]. IEEE Trans on Evolutionary Computation, 2007, 11(6): 712-731

[9]Storn R, Price K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359

[10]Abbass H A, Sarker R, Newton C. PDE: A Pareto frontier differential evolution approach for multi-objective optimization problems[C] //Proc of IEEE Congress on Evolutionary Computation, vol 2. Piscataway, NJ: IEEE, 2001: 831-836

[11]Madavan N K. Multiobjective optimization using a Pareto differential evolution approach[C] //Proc of IEEE Congress on Evolutionary Computation, vol 2. Piscataway, NJ: IEEE, 2002: 1145-1150

[12]Xue F, Sanderson A C, Graves R J. Pareto-based multi-objective differential evolution[C] //Proc of IEEE Congress on Evolutionary Computation, vol 2. Piscataway, NJ: IEEE, 2003: 862-869

[13]Robic T, Filipic B. DEMO: Differential evolution for multiobjective optimization[G] //LNCS 3410: Proc of Evolutionary Multi-Criterion Optimization. Berlin: Springer, 2005: 520-533

[14]Al-Qunaieer F S, Tizhoosh H R, Rahnamayan S. Opposition based computing—A survey[C] //Proc of the 6th IEEE World Congress on Computational Intelligence. Piscataway, NJ: IEEE, 2010: 1-7

[15]Xu Q Z, Wang L, Wang N, et al. A review of opposition-based learning from 2005 to 2012[J]. Engineering Applications of Artificial Intelligence, 2014, 29: 1-12

[16]Wang H. Opposition-based barebones particle swarm for constrained nonlinear optimization problems[J]. Mathematical Problems in Engineering, 2012, 2012: 1-12

[17]Wang H, Wu Z, Liu Y, et al. Space transformation search: A new evolutionary technique[C] //Proc of World Summit Genetic Evolutionary Computation. New York: ACM, 2009: 537-544

[18]Rahnamayan S, Tizhoosh H R, Salama M M A. Opposition-based differential evolution algorithms[C] //Proc of IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2006: 2010-2017

[19]Ahandani M A, Alavi-Rad H. Opposition-based learning in the shuffled differential evolution algorithm[J]. Soft Computing, 2012, 16(8): 1303-1337

[20]Omran M G H. CODEQ: An effective metaheuristic for continuous global optimization[J]. International Journal of Metaheuristics, 2010, 1(2): 108-131

[21]Miao X F, Mu D J, Han X W, et al. A hybrid differential evolution for numerical optimization[C] //Proc of Int Conf on Biomedical Engineering and Informatics. Piscataway, NJ: IEEE, 2009: 1-5

[22]Wang H, Rahnamayan S, Wu Z J. Parallel differential evolution with self adapting control parameters and generalized opposition-based learning for solving high-dimensional optimization problems[J]. Journal of Parallel Distributed Computing, 2013, 73(1): 62-73

[23]Omran M G H, Salman A. Constrained optimization using CODEQ[J]. Chaos, Solitons Fractals, 2009, 42(2): 662-668

[24]Peng L, Wang Y, Dai G. A novel opposition-based multi-objective differential evolution algorithm for multi-objective optimization[G] //LNCS 5370: Proc of Advances in Computation and Intelligence. Berlin: Springer, 2008: 162-170

[25]Dong N, Wang Y. Multiobjective differential evolution based on opposite operation[C] //Proc of Int Conf on Computational Intelligence and Security, vol 1. Piscataway, NJ: IEEE, 2009: 123-127

[26]Ray T, Tai K, Seow K C. An evolutionary algorithm for multiobjective optimization[J]. Engineering Optimization, 2001, 33(3): 399-424

[27]Wang Jianlin, Wu Jiahuan, Zhang Chaoran, et al. Constrained multi-objective particle swarm optimization algorithm based on self-adaptive evolutionary learning[J]. Control and Decision, 2014, 29(10): 1765-1770 (in Chinese)(王建林, 吴佳欢, 张超然, 等. 基于自适应进化学习的约束多目标粒子群优化算法[J]. 控制与决策, 2014, 29(10): 1765-1770)

[28]Binh T T, Korn U. MOBES: A multi-objective evolution strategy for constrained optimization problems[C] //Proc of the 3rd Int Conf on Genetic Algorithms. New York: ACM, 1997: 176-182

[29]Srinivas N, Deb K. Multi-objective function optimization using non-dominated sorting genetic algorithms[J]. Evolutionary Computation, 1994, 2(3): 221-248

[30]Tanaka M, Watanabe H, Furukawa Y, et al. GA-based decision support system for multi-criteria optimization[C] //Proc of Int Conf on Systems, Man and Cybernetics, vol 2. Piscataway, NJ: IEEE, 1995: 1556-1561

[31]Deb K, Pratap A, Meyarivan T. Constrained test problems for multi-objective evolutionary optimization[G] //LNCS 1993: Proc of Evolutionary Multi-Criterion Optimization. Berlin: Springer, 2001: 284-298

[32]Chen X, Du W, Qian F. Multi-objective differential evolution with ranking-based mutation operator and its application in chemical process optimization[J]. Chemometrics and Intelligent Laboratory Systems, 2014, 136: 85-96

[33]Zitzler E, Deb K, Thiele L. Comparison of multiobjective evolutionary algorithms: Empirical results[J]. Evolutionary Computation, 2000, 8(2): 173-195

[34]Zitzler E, Thiele L, Laumanns M, et al. Performance assessment of multiobjective optimizers: An analysis and review[J]. IEEE Trans on Evolutionary Computation, 2003, 7(2): 117-132

[35]Fonseca C M, Knowles J D, Thiele L, et al. A tutorial on the performance assessment of stochastic multiobjective optimizers[G] //LNCS 3410: Proc of the 3rd Int Conf on Evolutionary Multi-Criterion Optimization, vol 216. Berlin: Springer 2005: 240-258

Wei Wenhong, born in 1977. Associate professor in Dongguan University of Technology. His main research interests include evolutionary algorithms, multi-objective optimization and machine learning.

Wang Jiahai, born in 1977. Associate professor in Sun Yat-sen University. His main research interests include compu-tational intelligence and its applications.

Tao Ming, born in 1986. Associate professor in Dongguan University of Technology. His main research interests include intelligence computing and distributed computing.

Yuan Huaqiang, born in 1966. Professor in Dongguan University of Technology. His main research interests include intelligence computing.

Multi-Objective Constrained Differential Evolution Using Generalized Opposition-Based Learning

Wei Wenhong1, Wang Jiahai2, Tao Ming1, and Yuan Huaqiang1

1(ComputerInstitute,DongguanUniversityofTechnology,Dongguan,Guangdong523808)2(DepartmentofComputerScience,SunYat-senUniversity,Guangzhou510006)

AbstractDifferential evolution is a simple and efficient evolution algorithm to deal with nonlinear and complex optimization problems. Generalized opposition-based learning (GOBL) often guides population to evolve in the evolutionary computing. However, real-world problems are inherently constrained optimization problems often with multiple conflicting objectives. Hence, for resolving multi-objective constrained optimization problems, this paper proposes a constrained differential evolution algorithm using generalized opposition-based learning. In this algorithm, firstly, the transformed population is generated using general opposition-based learning in the population initialization. Secondly, the better individuals that are selected from the initial population and the transformed population using non-dominated sorting, crowding distance sorting and constraint handling techniques compose the new initial population. Lastly, based on a jumping probability, the transformed population is calculated again after generating new populations, and the fittest individuals that are selected from the union of the current population and the transformed population compose new population using the same techniques. The solution can be evolved toward Pareto front slowly according to the generalized opposition-based learning, so that the best solutions set can be found. The proposed algorithm is tested in multi-objective benchmark problems and compared with NSGA-Ⅱ, MOEA�D and other multi-objective evolution algorithms. The experimental results show that our algorithm is able to improve convergence speed and generate solutions which approximate to the best optimal Pareto front.

Key wordsdifferential evolution; generalized opposition-based learning (GOBL); multi-objective optimization; constrained optimization; non-dominated sorting

收稿日期：2015-09-08；修回日期：2015-12-30

基金项目：国家自然科学基金项目(61170216,61300198,61572131)；广东高校科技创新项目(2013KJCX0178)

通信作者：袁华强(hyuan66@163.com)

中图法分类号TP18

This work was supported by the National Natural Science Foundation of China (61170216, 61300198, 61572131) and the Guangdong Science and Technology Innovation Project of Higher Education (2013KJCX0178).