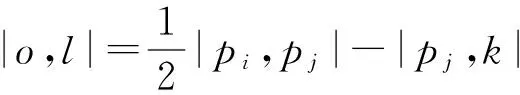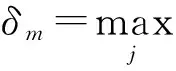EDDPC：一种高效的分布式密度中心聚类算法

巩树凤　　　张岩峰

(东北大学计算机科学与工程学院　沈阳　110819)(shidashufeng@163.com)



EDDPC：一种高效的分布式密度中心聚类算法

巩树凤张岩峰

(东北大学计算机科学与工程学院沈阳110819)(shidashufeng@163.com)

摘要聚类分析是数据挖掘中经常用到的一种分析数据之间关系的方法.它把数据对象集合划分成多个不同的组或簇，每个簇内的数据对象之间的相似性要高于与其他簇内的对象的相似性.密度中心聚类算法是一个最近发表在《Science》上的新型聚类算法，它通过评估每个数据对象的2个属性值(密度值ρ和斥群值δ)来进行聚类.相对于其他传统聚类算法，它的优越性体现在交互性、无迭代性、无数据分布依赖性等方面.但是密度中心聚类算法在计算每个数据对象的密度值和斥群值时，需要O(N2)复杂度的距离计算，当处理海量高维数据时，该算法的效率会受到很大的影响.为了提高该算法的效率和扩展性，提出一种高效的分布式密度中心聚类算法EDDPC (efficient distributed density peaks clustering)，它利用Voronoi分割与合理的数据复制及过滤，避免了大量无用的距离计算开销和数据传输开销.实验结果显示:与简单的MapReduce分布式实现比较，EDDPC可以达到40倍左右的性能提升.

关键词密度中心；数据聚类；Voronoi分割；MapReduce；大数据

聚类在很多应用中是一种基础的数据分析方法，例如社会网络分析、智能商务、图像模式识别、Web搜索和生物学等.当前存在很多聚类算法[1]，这其中包括基于划分的方法(如k-medoids[2]，k-means[3])、基于层次的方法(如AGNES[4])、基于密度的方法(如DBASCAN[5])、基于网格的方法(如STING[6])，还有面向大数据的快速自适应同步聚类算法FAKCS[7]等.

密度中心聚类算法[8]是由Alex和Alessandro最近在《Science》上提出的一个新型聚类算法.它区别于其他聚类算法，基于2点假设进行设计：1)聚类中心点的密度不低于它附近点的密度；2)聚类中心点与密度比它大的点(另一个聚类中的点)的距离非常远.在该算法的设计中每个点有2个属性: 1)密度值ρ；2)斥群值δ(与密度值比自己大的点的距离的最小值).密度值ρ越大说明该点越有可能是聚类中心，斥群值δ越大说明该点越有可能代表一个新的聚类，而只有当密度值ρ和斥群值δ都较大时，该点才更可能是某一个聚类的密度中心.算法根据这2个值的大小来选择密度中心点.

相对于诸多传统聚类算法，密度中心聚类算法具有3个优点：

1) 交互性.不同于k-means等聚类算法，要求用户在算法执行前指定聚类的个数k.密度中心聚类算法在计算出每个点的密度值ρ和斥群值δ之后，由用户根据ρ值和δ值来确定聚类的个数.

2) 无迭代性.与其他算法(例如EM clustering和k-means)相比，该算法只需要遍历1次数据集即可完成，不需要多次迭代.

3) 无数据分布依赖性.算法的聚类形状没有偏倚，可以适用于多种环境下数据的聚类[1].

尽管密度中心聚类算法有以上诸多优点，但是计算密度值ρ和斥群值δ需要测量数据集中任意2点之间的欧氏距离，复杂度为O(N2).当处理海量高维数据时，算法的实现涉及到大量的高维欧氏距离计算，造成大量的计算开销，使其无法在单机环境下运行，严重影响了算法的实用性.

针对以上问题，为了提高算法执行效率，本文基于MapReduce[9]实现了简单分布式密度中心聚类(simple distributed density peaks clustering, SDDPC)算法，该算法虽然可以利用多台节点分布式执行算法，但是仍然需要大量的距离计算开销和数据传输开销.我们把它作为待比较的基准方法，并提出了一种高效的分布式密度中心聚类(efficient distributed density peaks clustering, EDDPC)算法.它首先利用Voronoi分割将数据集分成几个互不相交的组，由于对象的密度值ρ和斥群值δ的计算可能会用到其他组中的数据，本文提出了高效的数据复制过滤模型，将一少部分满足特定条件的数据在分组间复制，过滤掉无用数据.各分组并行地根据分配数据和部分复制数据，在分组内局部计算各点的密度值ρ和斥群值δ，并从理论上保证结果的正确性，从而大大提高了算法的执行效率和可扩展性.

本文的主要贡献如下：

1) 提出了一种基于MapReduce的高效分布式密度中心聚类算法EDDPC，并且在开源的Hadoop框架上实现了该算法.

2) 针对ρ值计算，设计了一种数据复制模型；针对δ值计算，设计了2种数据过滤模型，从而减少了数据对象的复制量和距离计算量，提高了算法的执行效率.

3) 在多个真实数据集上对分布式密度中心聚类算法进行了实验和性能评估，实验结果验证了该算法的高效性.

1相关工作

本节首先简单介绍一下密度中心聚类算法，然后介绍用到的MapReduce编程模型和Voronoi图数据分割法.

1.1密度中心聚类算法介绍

密度中心聚类算法[8]基于数据点的密度值ρ和斥群值δ来对数据集进行聚类.

数据点i的密度值ρi为

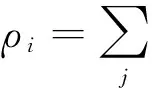
(1)

其中，χ(x)是一个函数，当x< 0时，χ(x)=1，否则χ(x)=0；dij是点j到点i的距离；dc是一个距离临界值.也就是说，ρi为与点i的距离小于dc的点的个数.

点i的斥群值δi为

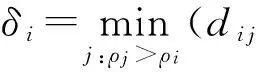
(2)

它代表与密度值比自己大的点的距离的最小值.假设密度比ρi大的点中，点j距离点i最近，那么δi=dij，而点j就是点i的依附点σi，

说明点i可以依附点j，归属于点j所属聚类.斥群值δi越小，点i距离点j越近，这种依附可能性越大，代表点i越有可能归属于点j所属的聚类；斥群值δi越大，点i距离点j越远依附性越小，说明点i很有可能是离群点或者是属于另一个聚类.当某个点m的密度值ρm是所有点中密度最大值，那么点m的斥群值δm=maxj(dmj).

密度中心聚类算法将每个数据点的ρ值和δ值表示在一个2维决策图(decision graph)上.如图1(a)展示了一个数据集的分布情况；图1(b)是根据图1(a)中每个点的ρ值和δ值绘制成的决策图.用户根据决策图中数据点的分布情况，圈出ρ值和δ值都很大的数据点作为密度中心，即决策图中右上角的部分数据点.由于在计算δ值时已经记录了每个数据点的依附点，可以根据数据点的依附关系并由用户选取的密度中心反推出每个数据点的所属聚类.

Fig. 1　Density peaks clustering.图1　密度中心聚类算法

1.2基于Voronoi图的分割法

Voronoi图，又叫泰森多边形或Dirichlet图，是一个关于空间划分的基础数据结构.基于Voronoi图的划分是指在给定的数据对象集S上，选择M个对象作为种子对象，这M个种子对象按照2点之间连线的垂直平分线将数据集S分割成M个互不相交的组，这M个分组称为“Voronoi cells”.数据集S中的每个元素按照距离被划分到距离自己最近的种子对象所在的分组中.

Voronoi图分割法在并行计算中应用非常广泛，文献[10]以Voronoi图分割为基础使用MapReduce框架解决在大数据情况下的范围搜索和KNN查询，如图2显示了一个Voronoi图将数据集分割成8个组的实例.文献[11]用Voronoi图分割法设计出了一种高效的分布式KNN连接算法.受此启发，本文提出的EDDPC算法应用Voronoi图分割法对数据集分割，使分割后的数据集分组能够在集群中的节点上局部计算密度值和斥群值.为方便以后叙述做如下定义：Voronoi图分割种子对象集合为，Pi表示种子对象pi所在的分组.

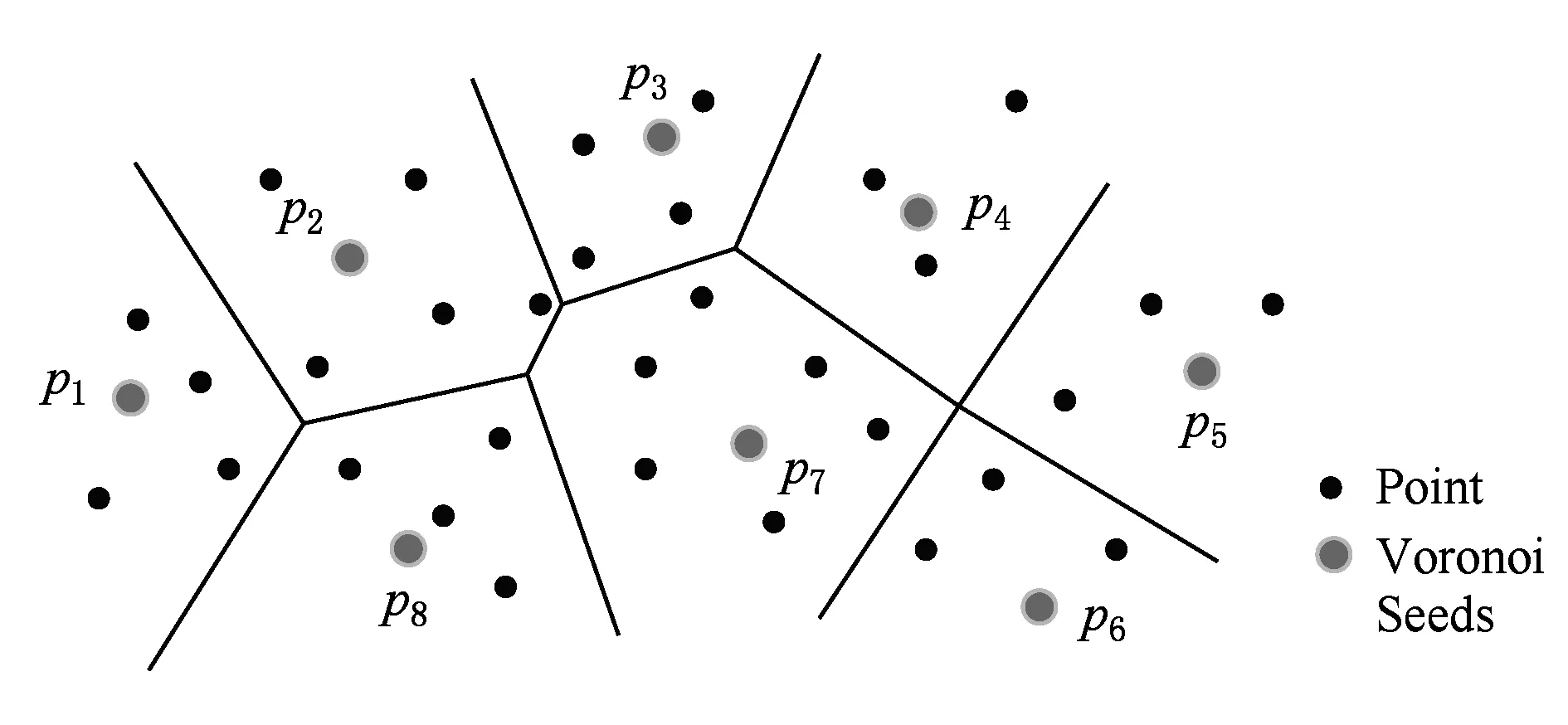
Fig. 2　An example of Voronoi.图2　Voronoi图示例

1.3MapReduce与Hadoop

MapReduce是一个当前流行的分布式编程模型.MapReduce提供了2个主要函数map和reduce.函数map和函数reduce由用户自己定义，函数map根据用户自定义的功能处理输入数据，并且以〈key,value〉的形式输出.MapReduce自动收集具有相同key值的value，并且以〈key,list(value)〉的形式作为reduce的输入，reduce根据用户定义的功能进行处理，最终以〈key,value〉的格式输出.MapReduce的大致工作流程为

map(k1,v1)→list(k2,v2)，

reduce(k2,list(v2))→list(k3,v3).

Hadoop是一个实现了MapReduce编程模型的开源框架.在Hadoop上的数据默认存储在分布式文件系统HDFS上.本文将基于MapReduce模型设计高效的分布式密度中心聚类算法.

2密度中心聚类在Hadoop上的简单实现

本节基于MapReduce框架实现基本的分布式密度中心聚类算法SDDPC.

在1.1节已经介绍过，密度中心聚类算法的主要步骤是计算每个点的密度值ρ和斥群值δ，因此分布式密度中心聚类算法的重点是分布式地计算ρ值和δ值.在得到每个数据点的ρ值和δ值后，可以将其收集到1台机器上绘出决策图进行聚类.接下来描述密度中心聚类算法的4个基本计算步骤：1)选择dc长度的预处理阶段(使用MapReduce);2)计算ρ值;3)根据ρ值计算出δ值;4)绘制决策图并对数据对象聚类.

2.1预处理：寻找合适dc

距离阈值dc在密度中心聚类算法的实现过程中是一个非常重要的参数，如式(1)所示该参数用来计算每个点的密度值ρ.文献[1]给出了一个dc的经验估计方法，即所有点对距离从大到小排序后的1%～2%处，因此本文参考该方法来选取dc值.

在大规模数据集下估计dc值是一个开销非常大的任务，即使在分布式环境中，对数据排序也是一个复杂的工作.因此，在本文中应用了采样的理念来对dc值进行估计.由于数据量大，因此我们基于MapReduce进行采样，函数map基于水塘采样(reservoir sampling)方法[12]对任意2点的距离进行分布式采样，由于样本数据少，所以可以将采集后的数据发送到单个reduce，由其进行距离计算并排序，然后选择出合适的dc值.

2.2计算ρ值

正如式(1)所示，ρo的计算需要知道对象o到其余每个点j∈S之间的距离doj.对象之间距离的计算在MapReduce中可以实现，有2种实现方法.在方法1中，函数map选出1个对象，然后将其发送给其他每个对象(假设总共有N个对象)；函数reduce收集每个对象上由map发过来的对象，计算该对象与它们之间的距离，并且根据式(1)计算出ρ值.显然这种简单的实现需要很大的开销，由于每个对象都需复制到其他对象所在机器进行距离计算，因此shuffle开销是O(N2)，计算开销也是O(N2).

由于在方法2中需要将数据分块，因此需要1个MapReduce作业来完成数据的分块，但是仍然比方法1效率高，尤其是当n≪N时，shuffle开销会急剧减少.在方法2中每个分块与其他n-1块运算，分块中的每个对象o就会得到n个ρ值，因此需要1个MapReduce作业来合并每个对象o的ρ值.

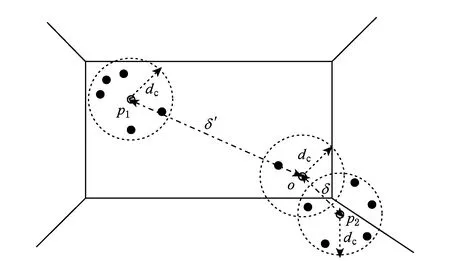
2.3计算δ值

δ值需要根据式(2)计算.算法实现步骤和计算ρ值时相似，需要2个MapReduce作业来完成δ值的计算，第1个MapReduce作业结束之后，每个对象会得到n个δ值，第2个MapReduce作业从这n个值中选出最小的一个值作为δ值.shuffle开销是O(n×N)，计算开销是O(N2).

2.4绘制决策图并聚类

将得到的ρ值集合和δ值集合汇集到1台机器上(ρ值集合和δ值集合的大小远小于点数据集S)，并基于得到的ρ值和δ值绘制决策图.用户根据ρ值和δ值的分布情况选出绘制在决策图中右上角的部分数据点作为聚类中心，每个点根据计算δ值时得到的依附关系，由聚类中心点反推出每个数据点的所属聚类.

3基于Voronoi分割和数据点复制过滤的高效分布式密度中心聚类算法

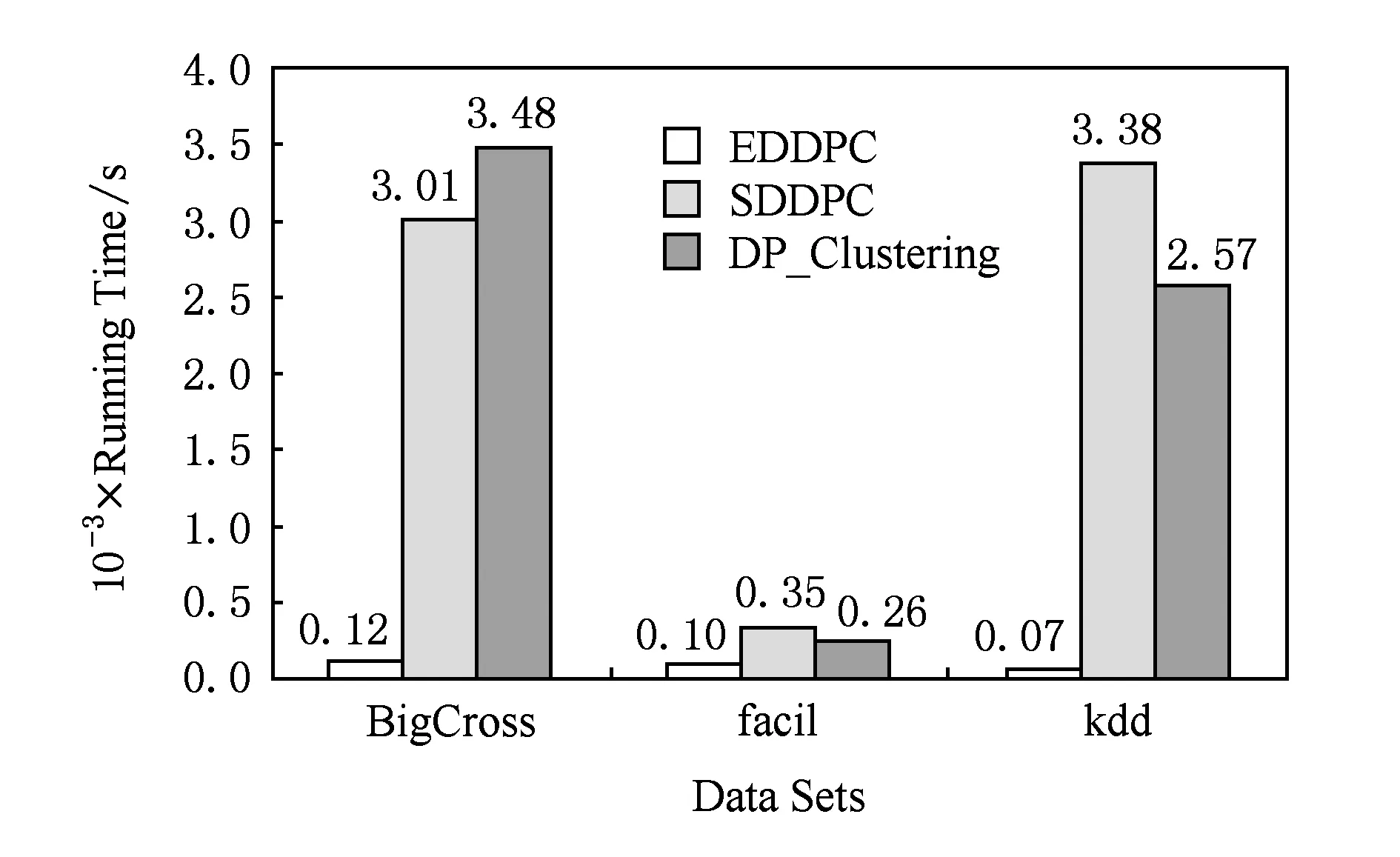
虽然我们设计了简单的分布式密度中心聚类算法SDDPC，弥补了单机运行时的缺陷，但是由于存在大量的shuffle开销和计算开销，因此并不是一种高效的方法.本节基于Voronoi数据分割提出了一种高效分布式密度中心聚类算法EDDPC.该算法包括1个预处理阶段和2个完整的MapReduce作业.EDDPC算法将数据分组后，各分组中的数据对象独立并行执行于集群中的各节点中，在分组内部局部计算ρ值和δ值，避免因计算所有对象间的距离而造成的大量开销.

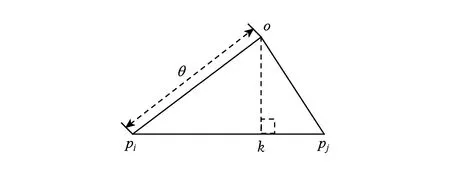
在预处理阶段需要完成的任务是选择Voronoi分割时所需要的种子.2个MapReduce作业分别用来计算ρ值和δ值.由于对数据分组之后，在某分组中计算某些对象的ρ值和δ值时需要其他分组的部分对象，因此各分组独立地直接计算ρ值和δ值将得到错误的结果.例如，对于某数据对象o∈Pi，在计算ρo时，|o,q|

3.1种子选择并且计算dc

EDDPC算法应用了1.2节提到的基于Voronoi图的分组方法.该分组方法使用点之间的距离关系来进行分组，是一个非常有效的空间分组方法，尤其是在高维空间上.

该分组方法根据种子对象进行分组，因此在分组之前需要先挑选出合适的种子对象.在挑选种子时使用2.1节中选择dc值时使用的水塘采样算法.在挑选种子对象的同时也能够得到dc值，无需额外的MapReduce作业.

3.2计算ρ值及其复制模型

经过预处理阶段的操作，可以得到Voronoi分组需要的种子对象集，然后创建1个MapReduce作业对数据集分组并计算ρ值.首先根据选出的种子对象进行分组，每个对象o与种子对象集中的每个对象pi计算距离，得到对象o到每个种子对象pi的距离dopi，比较对象o到每个种子对象的距离，选出距离o最近的种子对象pj，将对象o分配到pj所在的分组Pj中.

分组后，整个数据集分成若干个互不相交的组，因此，在计算对象o密度值ρo时，可能得到的是一个错误的值.如图3(a)所示,o靠近分组的边缘线时计算得到ρo=8，而实际值ρo=11.

Fig. 3　Example of replication.图3　数据复制示例

为了得到正确的ρo值需要将分组区域B中的3个点复制到区域A中.据此可以推出每个分组Si中的点不仅仅要包含由Voronoi分组后点集Pi，也要包含本组中的所有对象的邻居集合Ro.即

(3)

其中,Ro={q|∀q∈S,|q,o|

在分组之前无法得到对象o的dc邻居集合Ro包含哪些对象，但是根据Ro的定义可知，当q∈Ro时，|o,q|

我们提出保证分组正确计算ρ值的对象复制方案.如图3(b)所示，将所有距离边缘点小于dc的点全部发送到相邻的分组中，并由定理1保证其正确性.

定理1. ∀o∈Pj，那么对象o可能成为Pi中某个对象的Ro点而被复制到的Pi中的条件为

(4)

(5)

当|o,l|

证毕.

Fig. 4　An example of equation (5).图4　式(5)示例

式(5)中的|o,pi|，|o,pj|在对数据对象o进行分组时已经得出，|pi,pj|在种子选择时算出，由于种子对象数据量少，因此所有种子间的距离计算可以单机完成，并在分布式计算时加载使用.

根据定理1可在分组的同时对数据进行复制，分组完成后每个组内的数据会包含2种数据对象:一种是由Voronoi数据分割方法分组后在每个Voronoi cell里的对象集Pi，该集合中的对象称之为原始对象;另一种是为了计算原始对象的密度值ρ而将其他组中的数据复制进来的对象集Si-Pi，该集合中的对象称之为复制对象.

MapReduce实现：函数map首先加载事先采样得到的Voronoi种子对象集合，然后计算每个对象o到所有种子对象pi∈的距离|o,pi|，将该对象发送到距离最近的种子所在的分组中，即对象o所属的Voronoi分组.同时，函数map根据式(5)把满足复制条件的对象发送到邻居分组中.函数reduce负责某个Voronoi分组，根据式(1)计算每个原始对象的ρ值(无须计算复制对象的ρ值).假设α是复制因子，代表平均每个点的副本数量，如果共产生n个Voronoi分组，那么计算密度值ρ需要复制α×N个对象，所以shuffle开销是O(α×N)，而所需的距离计算开销是O(α×N2n) .

3.3复制过滤计算δ值

在得到密度值ρ之后，可以根据组内每个对象的ρ值和式(2)计算每个对象的δ值.只在分组内部计算δ值会有一定的局限性，算出的δ值并不是实际的δ值，而是一个不小于实际δ值的局部δ值，记为δ′.如图5所示，由于对象p2不在对象o所在的分组中，因此对象o在分组内部将p1点作为δ值依附点，最终算出的δ′就比实际的δ值大.

Fig. 5　δ value of object o.图5　对象o的δ值

为了能够求出精确的斥群值δ需要第2个MapReduce作业.如图5所示，为得到对象o的实际δ值，需要将组外的p2复制到对象o所在的分组中.因此为了计算每个组中对象的斥群值δ需要将一些组外的对象复制到本组中.由式(2)可知，对象o的斥群值δ是o与密度比自己大的对象的最小距离，若某对象的密度值大于分组Pi中对象密度的最小值，它便有可能成为Pi中某对象o的依附点σo.所以我们有如下引理：

引理1. ∀q∈Pj，则对象q可能成为分组Pi中某个对象的依附点σo的条件为

ρq>minρ(Pi),

(6)

其中minρ(Pi)=min{ρo|∀o∈Pi}.

在整个数据集S中符合式(6)的对象可能非常多，当Pi中含有整个数据集S中密度最小的对象时，需要将整个数据集全部复制到分组Pi中.但是，在所有满足式(6)的对象中也有很多对象是冗余的，这些冗余的对象导致一些额外数据复制开销和距离计算开销.因此，为了减少数据的复制量，需要将不必要的对象过滤.

为了计算组Pi中每个对象的δ值，经过复制后的分组Si不仅包含原始分组对象集Pi同时也应该含有每个对象的σo点，即：

(7)

在计算出ρ值之后，对本组内的原始对象根据ρ值进行局部δ′值计算.由于该分组未必包含原始对象o的依附点对象σo(最近的密度大于ρo的对象)，所以得到的δ′值是一个比实际值大的数值.但是这个值可以作为对象的斥群值δ的一个范围值，δ≤δ′.因此得到：

|o,σo|≤δ′.

(8)

3.3.1普通对象的依附点过滤模型

抛开分组内部的最大ρ值对象(局部密度中心点)，只考虑剩余普通对象的δ值的计算.

在第1个MapReduce作业中可以计算出普通对象的δ′值，它可以作为实际δ值的上界.在分组Pi中密度最大的对象的δ′值为无穷大，我们记次大的δ′为smaxδ(Pi)，则Pi中除局部密度中心点之外所有对象的依附点σo与分组种子的距离满足如下定理:

定理2. ∀o∈Pi，ρo≠maxρ(Pi)，记U(Pi)为集合Pi中的所有普通对象的δ值依附点σo到种子对象pi的距离最大值，那么U(Pi)满足不等式：

U(Pi)≤B(Pi)+smaxδ(Pi)，

(9)

其中,B(Pi)=max{|o,pi|,∀o∈Pi}.

证明. ∀o∈Pi，由于smaxδ(Pi)是除最大ρ值对象以外最大的δ′值，因此组内任何普通点的δ值不可能大于该值，所以|o,σo|≤smaxδ(Pi) ，又因为B(Pi)=max{|o,pi|,∀o∈Pi}，所以|pi,o|≤B(Pi)，由三角不等式|σo,pi|≤|pi,o|+|o,σo|,所以U(Pi)≤B(Pi)+smaxδ(Pi).

证毕.

式(9)说明了，Pi组内除最大ρ值对象的所有普通对象的依附点σo与该组的种子对象pi的距离上限为B(Pi)+smaxδ(Pi).由此我们得到如下的推论:

推论1. ∀o∈S，o∉Pi，则对象o可能成为Pi中某对象的σo点而被复制到Pi中的条件为

(10)

以上过滤模型没有复制分组中密度最大对象的依附点，接下来我们提出分组中最大密度对象的σo过滤模型.

3.3.2局部最大密度对象的依附点过滤模型

局部最大密度对象的依附点过滤模型同样要找到一个指导对象的依附点复制到组Pi的取值范围mU(Pi)，该取值范围不同于普通对象依附点过滤模型中的取值范围U(Pi).我们首先给出如下定理：

定理3. 给定1个分组Pi，对象m为该分组的局部最大密度对象，即ρm=maxρ(Pi)，假设其依附点为σm，则：

|pi,σm|≤min {2|m,pi|+|pj,u|+|pi,pj|}，

(11)

其中u∈Pj且ρu>ρm，pj≠pi，pj∈P.

证明. 根据三角不等式可知，|pi,σm|≤|pi,m|+|m,σm|，由σm的定义可得|m,σm|≤min {|m,u|}，所以|pi,σm|≤|m,pi|+min {|m,u|}，又因为|m,u|≤|m,pi|+|pi,u|，|pi,u|≤|pi,pj|+|pj,u|.所以|pi,Dm|≤min {2|m,pi|+|pj,u|+|pi,pj|}.

证毕.

由此得出如下推论：

推论2. ∀o∈S，o∉Pi，则对象o可能成为Pi中局部最大密度对象m的依附点σm而被复制到分组Pi中的条件为

(12)

其中，mU(Pi)=min {2|m,pi|+|pj,u|+|pi,pj|}.

在2个复制模型中涉及到每个分组内的次大δ′值smaxδ(Pi) (最大δ′值应该是无穷大)、组内的最大ρ值maxρ(Pi)、组内最小ρ值minρ(Pi)、组内局部最大ρ值对象m到种子对象的距离|m,pi|和距离该组的种子对象最远的点的距离B(Pi)，这些数据是在完成第1个MapReduce作业后需要收集的一些关于分组的信息.

2个过滤模型中的式(10)和式(12)都以|o,pi|≤θ的形式出现，其中θ=U(Pi)或θ=mU(Pi).

对每个对象决定是否要发送到分组Pi中，都要与pi做1次距离计算.因此，当P中的对象非常多时，开销也会变大，为此本文给出了一种剪枝的策略.

定理4. ∀o∈Pj，|o,pi|<θ，则|o,pj|>|pj,pi|-θ.

证明. 如图6所示，由直角三角形斜边大于直角边可知|pi,k|<θ，|pj,k|>|pj,pi|-θ，又因为|o,pj|>|pj,k|，|pj,k|>|pj,pi|-θ，所以|o,pj|>|pj,pi|-θ.

证毕.

因此当|o,pj|>|pj,pi|-θ时，不必计算o到pi的距离，而直接过滤.

Fig. 6　An example of theorem 4.图6　定理4示例

MapReduce实现：在第2个MapReduce作业中，函数map根据以上2个模型，将满足推论1和推论2的对象进行相应的复制和发送.这里需要注意一点，如果某一对象同时满足2个条件，为了避免重复计算，只将数据对象复制发送1次即可.在reduce阶段，只需要比较组内原始对象的密度与复制对象的密度，当密度比自己密度大时计算距离，选择最小距离作为δ值，同时记录δ值的依附点.假设β是复制因子，代表平均每个点的副本数量，如果共产生n个Voronoi分组，那么计算斥群值δ需要复制β×N个对象，所以shuffle开销是O(β×N)，而所需的距离计算开销是O(β×N2n).

4实验

我们在本地集群和Amazon EC2云平台上应用3个真实数据集对分布式密度中心算法SDDPC和优化的EDDPC算法进行了对比实验分析.

4.1实验环境

Hadoop本地集群包括4台slave机器、1台master机器，每台机器配有Intel I5-4690 3.3 GHz 4Core处理器、1000 Mbps以太网卡、1 TB 7200rm普通硬盘、4 GB运行内存.Amazon EC2集群包括17个m1.medium节点.操作系统为64位Ubuntu 14.04 LTS，JDK版本为Java1.7，Hadoop版本为Hadoop1.2.1.

数据集采用BigCross[13]，facial[14]，kdd[15]，其中BigCross数据集包含11 620 300个点，实验过程中只截取了50万个点，每条记录的维度是57；facial数据集包含27 936个点，每个点300维；kdd数据集包含145 751个点，每个点74维.

本文所有实验中SDDPC算法以200个点作为1个分块，EDDPC算法为避免因选择到的种子不同造成分组状态不同，从而导致实验结果不同而对实验效果造成影响，所以2种算法均采用3次实验取平均值作为最终结果.

4.2实验结果与分析

4.2.1整体性能评估

图7展示了在BigCross(随机截取20万个点)，facial，kdd数据集上SDDPC，EDDPC和原始的密度中心聚类(density peak clustering, DP_Clustering)算法运行时间的比较.EDDPC种子选取比例为3‰，运行时间不包括绘制决策图时间.总体上从图7可以看出,EDDPC算法的运行时间明显要少于SDDPC算法，尤其在数据量比较大的BigCross和kdd数据集上.在kdd数据集上表现最为明显，产生kdd运行时间差距的原因是kdd数据集中只有1个聚类簇，因此在计算δ值时shuffle开销和计算开销大大减少.原始DP_Clustering算法在单机环境下运行，由于没有Hadoop启动时间和多次读文件的时间，因此原始DP_Clustering算法在数据量比较小的情况下会比SDDPC算法的运行时间快；而在数据量比较大的情况下，原始DP_Clustering算法由于是在单机环境下执行，会造成内存溢出，从而无法执行DP_Clustering算法.

Fig. 7　Running time comparison on three data sets.图7　3种数据集下运行时间比较

4.2.2数据集大小的影响

为了测试数据集大小变化对算法性能的影响，我们从BigCross数据集中分别随机截取了10万、20万、30万、40万、50万个数据对象，分别构成了5个大小不同的数据集.如图8显示了EDDPC和SDDPC算法在这5个数据集上运行时间的对比，可以看出改进的EDDPC算法时间增长比较缓慢，而SDDPC算法以接近平方的速度增长.

Fig. 8　Running time comparison when varying data size.图8　不同数据集大小情况下的运行时间比较

为了分析造成运行时间差距的原因，本文还统计了这2种算法在Hadoop框架上执行时的通信量(shuffling cost)、每个点的副本个数和点之间距离计算的次数.

图9显示了在计算ρ值和δ值时EDDPC和SDDPC算法执行过程中每个点的平均副本数量.其中EDDPC算法的副本数量由程序统计而得，并多次统计取平均值；SDDPC算法的副本数量根据Nn计算得到，其中N指数据集中点的个数，n指每个分块中包含的点的个数.

Fig. 9　Comparison of number of points replicas.图9　点副本数比较

图10显示了在输入数据为10万～50万时EDDPC和SDDPC算法在Hadoop上执行过程中的通信量.

图11显示了数据从100×103～500×103时，EDDPC和SDDPC算法在Hadoop集群上执行过程中计算2点之间距离的计算次数，EDDPC算法由程序统计，SDDPC算法根据公式2N×(N-1)计算.

通过分析图9可以看到，EDDPC算法在计算ρ值和δ值的过程中平均每个点的副本数量比SDDPC算法要少，因此Hadoop集群中各节点之间的通信量机会变少，如图10所示.同时由于副本数量的减少和组内各点局部计算距离，从而减少距离计算的次数，如图11所示.

Fig. 10　Shuffling cost comparison.图10　Shuffle通信量比较

Fig. 11　Comparison of distance measurements.图11　距离计算次数比较

4.2.3分组种子数量的影响

为了探究EDDPC算法中种子数量对算法执行效率的影响，本文设计了在相同数据量的点集中相同数据集(facial)下不同种子数量对实验结果造成的影响.

Fig. 12　Running time of EDDPC when varying numberof Voronoi partitions.图12　EDDPC中Voronoi分组数量不同时的运行时间

图12显示了在种子数量在5～95范围内变化时EDDPC算法的运行时间，由于选取到的种子不同，造成运行时间不同，因此本实验取3次实验的平均值作为本实验的结果值.

由图12可以看出，在一定范围内，随种子对象的增多运行时间先变少然后增大.种子对象在15～25时运行时间最少.由于种子对象的选取可能造成运行时间波动，但是大致趋势仍然是先变小后变大.

我们对图12所示现象做如下的分析：当种子对象增多时，数据分组变多，分组内部的数据会减少，因此在计算ρ值时分组内部距离计算的开销就会减少.而在计算δ值时，随着分组的增多，U(Pi)和mU(Pi)的值会变小，每个分组内部被复制添加进来的数据对象会减少，因此总体运行时间会减少.但是随着种子对象的持续增加，分组数量增多，map和reduce的线程数量就会增加，加大了系统的开销.同时分组的增多也会使每个对象被复制到其他组的概率变大，因此通信开销也会随之增长,导致运行时间变长.

4.2.4集群数量的影响

我们在Amazon EC2集群上，分别利用2,4,8,16个计算节点运行EDDPC算法来评估算法扩展性能.采用BigCross数据集中截取的50万条数据作为输入数据，实验结果如图13所示.我们以2节点运行时间为基准，画出了一条理论最优的扩展性能曲线.从图13可以看出,EDDPC算法具有不错的扩展性能，虽然性能加速比略低于理论最优的加速比，但是从4节点到16节点的运行时间几乎是随着节点数量的增加呈线性递减.

Fig. 13　Running time of EDDPC when varying number of nodes.图13　节点不同时的EDDPC运行时间

5结论

本文发现了密度中心聚类算法的运行效率问题，并基于MapReduce简单实现了分布式密度中心聚类算法——SDDPC.为了进一步提高SDDPC算法的性能，本文基于Voronoi图分割的方法提出一种高效的分布式密度中心聚类算法——EDDPC.为了正确计算ρ值和δ值，本文分别给出了一个数据对象复制模型和2个数据对象过滤模型，将部分其他分组内的必要对象复制到本分组内，这保证了EDDPC算法可以在各独立分组内分布式执行ρ值和δ值的计算.提出的高效数据复制过滤模型不仅能保证算法执行过程中能够精确计算每个对象的ρ值和δ值，从而得到与原始DP_Clustering算法相等的结果，同时大大减少了数据对象的副本数量和shuffling的开销，进而减少了计算量，使EDDPC算法能够在分布式情况下高效率执行.

参考文献

[1]Xu Rui, Wunsch D Ⅱ. Survey of clustering algorithms[J]. IEEE Trans on Neural Networks, 2005, 16(3): 645-678

[2]Kaufman L, Peter R. Clustering by Means of Medoids[G] //Statistical Data Analysis Based on the L1 Norm and Related Methods. North-Holland: North-Holland Press, 1987: 405-416

[3] MacQueen J. Some methods for classification and analysis of multivariate observations[C] //Proc of the 5th Berkeley Symp on Mathematical Statistics and Probability. Berkeley, CA: University of California Press, 1967: 281-297

[4]Zhang W, Wang X, Zhao D, et al. Graph Degree Linkage: Agglomerative Clustering on a Directed Graph[M] . Berlin: Springer, 2012: 428-441

[5] Ester M, Kriegel H P, Sander J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C] //Proc of ACM KDD’96. New York: ACM, 1996: 226-231

[6]Wang W, Jiong Y, Muntz R. STING: A statistical information grid approach to spatial data mining[C] //Proc of VLDB’97. San Francisco, CA: Morgan Kaufmann, 1997: 186-195

[7]Ying Wenhao, Xu Min, Wang Shitong, et al. Fast adaptive clustering by synchronization on large scale datasets[J].

Journal of Computer Research and Development, 2014, 51(4): 707-720 (in Chinese)(应文豪, 许敏, 王士同, 等. 在大规模数据集上进行快速自适应同步聚类[J]. 计算机研究与发展, 2015, 51(4): 707-720)

[8]Alex R, Alessandro L. Clustering by fast search and find of density peaks [J]. Science, 2014, 344(1492):1492-1496

[9]Jeffrey D, Sanjay G. MapReduce: Simplified data processing on large clusters[J]. Communications of the ACM, 2004, 51(1): 107-113

[10]Akdogan A, Demiryurek U, Banaei-Kashani F, et al. Voronoi-based geospatial query processing with MapReduce[C] //Proc of CloudCom ’10. Piscataway, NJ: IEEE, 2010: 9-16

[11]Lu Wei, Shen Yanyan, Chen Su, etc. Efficient processing ofknearest neighbor joins using MapReduce [J]. VLDB Endowment, 2012, 5(10): 1016-1027

[12]Jeffery S V. Random sampling with a reservoir [J]. ACM Trans on Mathematical Software, 1985, 11(1): 37-57

[13]Shindler M, Wong A, Meyerson A W. Fast and accuratek-means for large datasets[C] //Proc of NIPS’11. New York: Curran Associates Press, 2011: 2375-2383

[14]Freitas F A, Peres S M, Lima C A M, et al. Grammatical facial expressions recognition with machine learning[C] //Proc of FLAIRS’14. Menlo Park, CA: AAAI Press, 2014: 180-185

[15]Caruana R, Joachims T. Kddcup 04 biology dataset[EB/OL]. 2008 [2015-05-10]. http://kodiak.cs.cornell.edu/kddcup/datasets.html

Gong Shufeng, born in 1991. Master candidate. His main research interests include big data and cloud computing.

Zhang Yanfeng, born in 1982. Associate professor. Member of China Computer Federation. His main research interests include big data and cloud computing.

EDDPC: An Efficient Distributed Density Peaks Clustering Algorithm

Gong Shufeng and Zhang Yanfeng

(CollegeofComputerScienceandEngineering,NortheasternUniversity,Shenyang110819)

AbstractClustering is a commonly used method for data relationship analytics in data mining. The clustering algorithm divides a set of objects into several groups (clusters), and the data objects in the same group are more similar to each other than to those in other groups. Density peaks clustering is a recently proposed clustering algorithm published in Science magazine, which performs clustering in terms of each data object’sρvalue andδvalue. It exhibits its superiority over the other traditional clustering algorithms in interactivity, non-iterative process, and non-assumption on data distribution. However, computing each data object’sρandδvalue requires to measure distance between any pair of objects with high computational cost ofO(N2). This limits the practicability of this algorithm when clustering high-volume and high-dimensional data set. In order to improve efficiency and scalability, we propose an efficient distributed density peaks clustering algorithm—EDDPC, which leverages Voronoi diagram and careful data replication�filtering to reduce huge amount of useless distance measurement cost and data shuffle cost. Our results show that our EDDPC algorithm can improve the performance significantly (up to 40x) compared with naive MapReduce implementation.

Key wordsdensity peaks; data clustering; Voronoi partition; MapReduce; big data

收稿日期：2015-06-30；修回日期：2015-10-29

基金项目：国家自然科学基金项目(61300023,61528203,61272179)；中央高校基本科研业务费专项资金项目(N141605001,N120816001)

通信作者：张岩峰(zhangyf@cc.neu.edu.cn)

中图法分类号TP301.6

This work was supported by the National Natural Science Foundation of China (61300023,61528203,61272179) and the Fundamental Research Funds for the Central Universities (N141605001,N120816001)