基于QR分解的Contourlet域鲁棒盲水印算法

刘　海　陈　军,2

1(武汉大学国家多媒体软件工程技术研究中心　湖北 武汉 430072)2(武汉大学深圳研究院　广东 深圳 518063)



基于QR分解的Contourlet域鲁棒盲水印算法

刘海1陈军1,2

1(武汉大学国家多媒体软件工程技术研究中心湖北 武汉 430072)2(武汉大学深圳研究院广东 深圳 518063)

摘要为了提高变换域数字水印的鲁棒性，提出一种基于QR分解的Contourlet域鲁棒盲水印算法。该算法首先对二值水印图像进行Arnold置乱预处理，然后对宿主图像进行Contourlet变换，提取低频子带进行不重叠的分块，最后对每个子块依次进行QR分解，采用自适应量化策略在上三角R矩阵的第1行元素上重复嵌入1 bit水印信息。在水印提取时，根据多数原则从每个子块提取相应的1 bit水印信息。实验结果表明，该算法在取得良好不可见性的同时，对JPEG压缩、噪声、滤波、缩放和剪切等多种攻击具有较强的鲁棒性，并且可以实现水印的盲提取。

关键词数字水印Contourlet变换QR分解鲁棒性盲水印

0引言

虽然互联网发展迅猛，给人们的工作和生活带来了便利，但是随之而来的版权问题也越来越明显：人们更容易获取他人在互联网上发布的原创作品，甚至对其任意复制和修改，严重损害原创作者的权益。数字水印作为版权保护的一种手段，越来越显现出其巨大的潜能和众多的优势，发展成为学术界的研究热点，并取得了丰硕的成果。

目前数字水印的研究大多基于变换域，而相比于其他变换域方法，小波变换因其具有良好的多分辨率和时频局部特性而应用更为广泛。2002年，Do等人提出了一种新的多尺度几何变换方法，即Contourlet变换[1]。Contourlet变换具有小波变换不具备的各向异性，并且提供了更高水平的方向性，从而可以更全面地表示图像本身的奇异几何特性。因此，基于Contourlet变换的数字水印逐渐成为研究的热点。近年来，矩阵分解方法被应用于数字水印领域，主要包括SVD分解、Schur分解和NMF分解等。这些矩阵分解方法具有的优良特性使水印算法的鲁棒性得到了显著的提高。QR分解也作为一种强有力的矩阵分解方法和数值分析技术，具有运算复杂度低、数值稳定性好等特点，也被逐渐应用于数字水印的研究[2～5]。文献[2]在小波域应用QR分解，首先对水印图像进行QR分解得到正交矩阵Q和上三角矩阵R，然后利用Q矩阵的正交特性和R矩阵的能量分布特性，将它们分别嵌入到宿主图像小波变换后的低频子带和对角方向子带中，取得了较强的鲁棒性和不可见性。文献[3]证明了QR分解后的正交矩阵Q的第1列元素具有不变特性，利用第1列元素间大小关系的稳定性量化嵌入水印信息，取得了较强的鲁棒性，但不足的是Q矩阵代表了原图像矩阵像素间的关系，对其进行修改容易导致图像失真。文献[4]将QR分解和SVD分解相结合应用于Contourlet域，首先对水印图像Contourlet变换后的低频子带进行QR分解，然后对R矩阵进行SVD分解，最后将得到的奇异值作为水印信息嵌入到宿主图像低频子带的奇异值中，取得了很强的鲁棒性。但该算法在提取水印时需要较多关于宿主图像和水印图像的信息，可能存在SVD分解的高虚警率问题，而且算法较为复杂。文献[5]采用分块QR分解的方法将水印图像嵌入到宿主图像Contourlet域的低频子带，该算法在水印提取时同样过多地依赖于宿主图像和水印图像的信息。

本文提出一种新的在Contourlet域利用QR分解的数字图像水印算法。该算法选择宿主图像Contourlet变换后的低频子带作为水印嵌入子带，并利用QR分解的上三角R矩阵的能量分布特性和数值稳定性，将水印信息自适应量化嵌入分块R矩阵的第1行元素。实验结果表明，本文算法在取得良好不可见性的同时，具有较强的鲁棒性。

1水印算法原理

1.1Contourlet变换

Contourlet变换是一种基于图像的几何分析方法，具有多分辨率、局部化、多方向性和各向异性等优良特性。与小波变换相比，Contourlet变换能提供更多的方向信息，能更稀疏地表示图像的平滑轮廓，具有高水平的各向异性，弥补了小波变换不能最优地表示含线或面奇异的高维函数的不足[6]。

离散的Contourlet变换称为塔形方向滤波器组PDFB(PyramidDirectionalFilterBanks)，它是由拉普拉斯金字塔分解LP(LaplacianPyramid)和方向滤波器组DFB(DirectionalFilterBanks)组成的双层滤波器结构。Contourlet变换将多尺度分析和方向分析分开进行，首先用LP进行多尺度分解，以捕获点奇异性，然后用DFB将分布在同一方向上的奇异点合成为一个系数，以捕获方向性。这个过程在粗糙图像上重复进行，从而将图像分解为多尺度多方向子带。Contourlet变换的过程如图1所示。图2给出了512×512的灰度图像Lena在进行二级Contourlet变换后的效果，其中包括1个低频子带、4个中频方向子带和8个高频方向子带。

图1　Contourlet变换的过程

图2　Lena二级Contourlet变换的效果图

1.2矩阵QR分解

定义1如果实(复)非奇异矩阵A能够化成正交(酉)矩阵Q与实(复)非奇异上三角矩阵R的乘积，即：

A=QR

(1)

则称式(1)为A的QR分解。

定理1设A是n阶实(复)非奇异矩阵，则存在Q和R使A有QR分解；且除去相差一个对角元素的绝对值(模)全等于1的对角矩阵因子外，分解是唯一的[7]。

由上述定义和定理可知，对于双精度图像矩阵，无论行数和列数是否相等，都可以进行QR分解。通过实验发现，图像矩阵经QR分解以后得到的上三角R矩阵的第1行元素值较大，集中了图像的绝大部分能量，适合嵌入水印，具有较大的嵌入范围，而且QR分解具有的数值稳定性，可以为水印提供更好的鲁棒性。

2基于QR分解的Contourlet域水印算法

本文算法对水印图像进行Arnold置乱预处理，以提高水印图像的安全性[8]。由于宿主图像Contourlet变换后的低频子带集中了图像的绝大部分能量，常规处理对低频子带系数的影响较小，因此选择低频子带作为水印嵌入子带。然而低频子带系数的变化也容易导致图像的失真，因此对低频子带进行不重叠的分块，根据各子块能量分布特性，进行自适应量化嵌入水印，保证水印鲁棒性和不可见性的折中。为了进一步提高水印算法的鲁棒性，利用QR分解的上三角R矩阵优良的能量分布特性和数值稳定性，选择各子块R矩阵的第1行元素作为水印嵌入位置，并采用重复嵌入的思想[9]在每个子块嵌入1bit水印信息。在水印提取时，根据多数原则依次从每个子块提取相应的1bit水印信息，最终获得嵌入的二值水印图像。

2.1水印的嵌入

设宿主图像为X={x(i,j)|1≤i≤m,1≤j≤n}，二值水印图像为W={w(i,j)|1≤i≤p,1≤j≤q}。水印嵌入步骤如下：

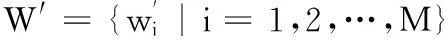
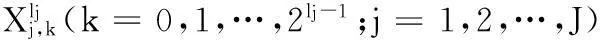
3) 将低频子带XJ划分成M个N×N大小的不重叠的子块，记为Ai(i=1,2,…,M)。

4) 依次对各子块Ai进行QR分解：

[Qi,Ri]=qr(Ai)

(2)

其中qr(·)表示QR分解函数，Qi和Ri分别表示Ai进行QR分解后的Q矩阵和R矩阵。

5) 选择各子块R矩阵的第1行元素，记为δi,j(i=1,2,…,M;j=1,2,…,N)重复自适应量化嵌入1bit水印信息，量化公式为：

λi,j=floor(δi,j/δi)

(3)

其中floor(·)表示向下取整函数，δi为第i个子块的自适应量化步长。

考虑人类视觉特性和不同宿主图像纹理的差异，采用分块能量自适应调整量化步长[6]，δi为：

δi=(log2Ei×1000)/1000+δ0

(4)

(5)

其中δ0为基础量化步长，Ai(x,y)为子块元素。

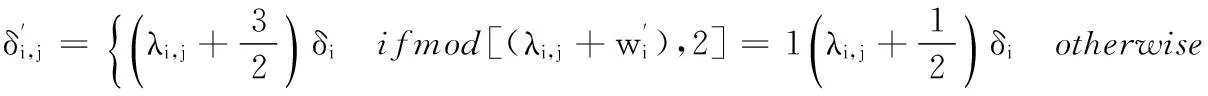
(6)

(7)

水印嵌入的核心代码如下：

%宿主图像Contourlet变换

coeffs=pdfbdec(double(im),pfilter,dfilter,nlevels);

low=coeffs{1};

%提取低频子带

n= 32;

%子带分块个数n*n

s= 4;

%子块大小s*s

q= 30;

%基础量化步长

l= 1;

%水印信息位序号

fori= 1:n

forj= 1:n

[Q,R] =qr(b_im{i,j});

%分块QR分解

fork= 1:s

ifl<=c*d

m=floor(R(1,k)/su(i,j));

h=mod(m+w(l),2);

ifh== 1

R(1,k) = (m+3/2)*su(i,j);

else

R(1,k) = (m+1/2)*su(i,j);

end

end

end

b_im{i,j} =Q*R;

%QR逆变换

l=l+1;

end

end

coeffs{1} =low;

%所有子块合成为低频子带

%Contourlet逆变换得到含水印图像

imrec=pdfbrec(coeffs,pfilter,dfilter);

2.2水印的提取

本文是盲水印算法。水印提取步骤如下：

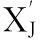
(8)

(9)

(10)

4) 将一维水印序列W′升维成二维图像，然后进行T-t次Arnold逆置乱变换，得到二值水印图像W。

水印提取的核心代码如下：

%含水印图像Contourlet变换

coeffs=pdfbdec(double(imrec),pfilter,dfilter,nlevels);

low=coeffs{1};

%提取低频子带

n= 32;

%子带分块个数n*n

s= 4;

%子块大小s*s

q= 30;

%基础量化步长

l= 1;

%水印信息位序号

fori= 1:n

forj= 1:n

[Q,R] =qr(b_im{i,j});

%分块QR分解

n0 = 0;

%水印信息位为0的个数

n1 = 0;

%水印信息位为1的个数

fork= 1:s

ifl<=c*d

m=floor(R(1,k)/su(i,j));

h=mod(m,2);

ifh== 1

n1 =n1+1;

else

n0 =n0+1;

end

end

end

%根据多数原则提取1bit水印信息位

ifn1 >=n0

w(l) = 1;

else

w(l) = 0;

end

l=l+1;

end

end

3实验和分析

本文实验在WindowsXPSP3和Matlab7.0平台上实现，以512×512的标准灰度图像Lena作为宿主图像，32×32的“CS”字样的二值图像作为水印图像。水印图像的嵌入区域为宿主图像二级Contourlet变换后的128×128的低频子带。Contourlet变换的LP和DFB滤波器分别采用“9-7”和“pkva”滤波器。水印Arnold置乱次数t为12，低频子带分块大小为4×4，基础量化步长δ0为30。

3.1不可见性实验

本文采用峰值信噪比(PSNR)作为不可见性的评价指标，PSNR从客观上衡量了含水印图像的视觉质量，其定义为：

(11)

其中I(i,j)表示原始宿主图像，I′(i,j)表示含水印图像，图像大小为M×N。PSNR值越大，表示宿主图像嵌入水印后视觉质量变化越小，不可见性也就越好。

图3中(a)为原始Lena图像，(b)为含水印Lena图像，(c)～(e)分别为原始二值水印图像、Arnold置乱后的水印图像、直接提取的水印图像。首先，从视觉效果上来看含水印图像并未出现任何的失真现象，与原始图像非常接近。另外，根据式(11)，本文计算出含水印图像的PSNR值为41.0694。这表明本文算法可以较好地对水印图像进行隐藏，从主观和客观的角度来看，都表现出良好的不可见性。

图3　水印嵌入和提取效果图

3.2鲁棒性实验

本文采用归一化相关系数(NC)作为鲁棒性的评价指标，NC定量地表示了水印图像的相似程度，其定义为：

(12)

其中W(i,j)表示原始水印图像，W′(i,j)表示提取的水印图像，水印图像大小为M×N。NC值越大，表示提取的水印图像与原始水印图像越相似，鲁棒性也就越好。根据式(12)，本文算法从没有受到任何攻击的含水印图像中提取的水印图像的NC值为1，这表明本文算法可以正确而完整地提取出所嵌入的水印图像。

3.2.1本文算法的鲁棒性验证

本文分别在JPEG压缩、噪声、滤波、缩放和剪切等攻击方式下对含水印图像进行鲁棒性实验，并对实验结果进行分析，进而从水印图像的NC值和视觉效果两方面验证本文算法的鲁棒性。

(1) JPEG压缩攻击

通过改变品质因子的方式对含水印图像进行JPEG压缩攻击，实验结果如表1所示。从表1可以看出本文算法对于较高品质(30及以上)的含水印图像均能完整地提取出水印图像，而对于低品质(30以下)的含水印图像依然提取出效果很好的水印图像，可见本文算法具有很强的抗JPEG压缩攻击的能力。

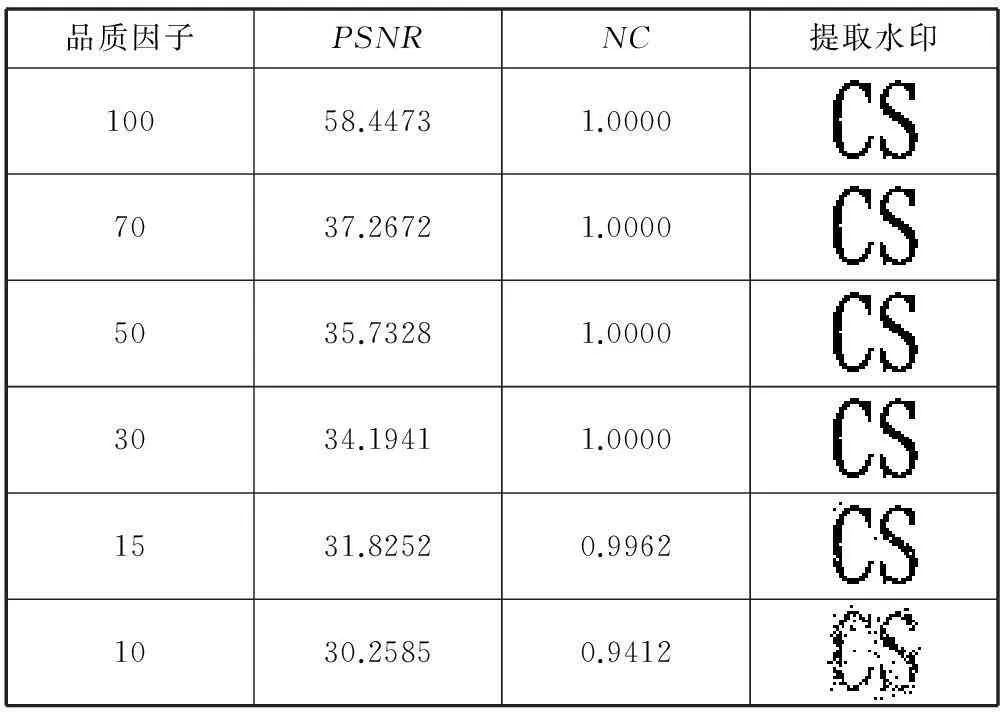
表1　抗JPEG压缩攻击实验结果表

(2) 噪声攻击

含水印图像在使用和传输过程中，不可避免地会受到各种噪声的干扰和影响，成为含噪声图像。表2列出了含水印图像在不同强度的高斯噪声、椒盐噪声和乘性噪声等攻击下的实验结果，可以看出本文算法对各种噪声攻击均具有较强的鲁棒性。

表2　抗噪声攻击实验结果表

(3) 滤波攻击

对含水印图像分别进行3×3和5×5窗口大小的中值滤波、均值滤波、高斯滤波和维纳滤波攻击。从表3可以看出本文算法在这些滤波攻击下都可以提取出效果很好的水印图像，表明本文算法对于常规的滤波攻击具有很强的鲁棒性。

表3　抗滤波攻击实验结果表

续表3

(4) 几何攻击

含水印图像也很容易受到几何攻击(如缩放、剪切等)，并且对含水印图像影响较大。对含水印图像分别进行不同倍数的缩放攻击和几种类型的剪切攻击，实验结果如表4所示。可以看出本文算法对缩放攻击和剪切攻击表现出一定的鲁棒性。图4给出了含水印图像在剪切攻击下的示意图。

表4　抗几何攻击实验结果表

图4　剪切攻击下的含水印图像

3.2.2与其他算法的对比

为了进一步验证本文算法较强的鲁棒性，与文献[10]提出的Contourlet域水印算法进行了对比实验，得出了几种典型攻击方式下的结果，如表5所示。可以看出本文算法在JPEG压缩、噪声、滤波、缩放和移除行列攻击下的鲁棒性比文献[10]明显要好。由于文献[10]采用了图像归一化方法，在水印嵌入前就将宿主图像映射到了几何不变区域，因此在旋转攻击下的鲁棒性优于本文算法。

表5　本文算法与文献[10]实验结果对比表

4结语

本文结合QR分解和Contourlet变换的优点，提出了一种新的鲁棒盲水印算法。其主要特点如下：a) 选择能量最大的低频子带作为水印嵌入子带，算法的鲁棒性得到了有力的保证；b) 利用QR分解的上三角R矩阵的能量分布特性和数值稳定性，选择第1行元素嵌入水印，提高了算法的鲁棒性；c) 根据人类视觉特性和分块能量分布特性，自适应量化嵌入水印信息，保证了鲁棒性和不可见性的折中，实现了水印的盲提取；d) 采用重复嵌入思想和多数原则提取水印，提高了水印的提取率。大量实验表明，本文提出的水印算法是一个可行的水印方案，在保证良好不可见性的同时，取得了较强的鲁棒性。但本文算法难以抵抗旋转攻击，有待进一步研究。

参考文献

[1]DoMN,VetterliM.TheContourlettransform:anefficientdirectionalmultiresolutionimagerepresentation[J].IEEETransactionsonImageProcessing,2005,14(12):2091-2106.

[2] 王树梅,赵卫东,王志成.一种基于QR分解的DWT域水印算法[J].微电子学与计算机,2008,25(5):51-55.

[3]SongWei,HouJianjun,LiZhaohong,etal.ChaoticsystemandQRfactorizationbasedrobustdigitalimagewatermarkingalgorithm[J].JournalofCentralSouthUniversityofTechnology,2011,18(1):116-124.

[4]MitraP,GunjanR,GaurMS.AmultiresolutionwatermarkingbasedonContourlettransformusingSVDandQRdecomposition[C]//Proc.ofIEEEInternationalConferenceonRecentAdvancesinComputingandSoftwareSystems.Chennai,India,2012:135-140.

[5]MitraP,GunjanR.AstatisticalpropertybasedimagewatermarkingusingpermutationandCT-QR[C]//Proc.ofIEEEInternationalConferenceonComputerCommunicationandInformatics.Coimbatore,India,2013:1-6.

[6] 朱少敏,刘建民.基于Contourlet变换域的自适应量化索引调制数字图像水印算法[J].光学学报,2009,29(6):1523-1529.

[7] 韩绍程,张兆宁,张玉金.基于非下采样剪切波变换和QR分解的鲁棒零水印算法[J].光电子·激光,2012,23(10):1957-1964.

[8] 姚蕾,王玲,李燕.基于NSCT-SVD的多重数字水印算法[J].计算机工程,2014,40(7):106-109.

[9] 李旭东.抗几何攻击的空间域图像数字水印算法[J].自动化学报,2008,34(7):832-837.

[10]ZhuDandan,TongQiang.AnewimagewatermarkingalgorithmusingCTandnormalization[C]//Proc.ofIEEEInternationalConferenceonSystems,Man,andCybernetics.Seoul,Korea,2012:3239-3244.

ROBUST BLIND WATERMARKING ALGORITHM IN CONTOURLET DOMAIN BASEDONQRDECOMPOSITION

Liu Hai1Chen Jun1,2

1(National Engineering Research Center for Multimedia Software,Wuhan University,Wuhan 430072,Hubei,China)2(Research Institute of Wuhan University in Shenzhen,Shenzhen 518063,Guangdong,China)

AbstractIn order to improve the robustness of digital watermarking in transform domain, this paper proposes a QR decomposition-based robust blind watermarking scheme in Contourlet domain. The scheme makes pre-treatment on original binary watermark image with Arnold scrambling first, and then conducts Contourlet transform on host image followed by extracting low frequency sub-band to divide it into non-overlapping sub-blocks, finally it applies the QR decomposition to each sub-block in turn, and repeatedly embeds one bit of watermark information into the first row elements of upper triangular R matrix using adaptive quantisation strategy. In watermark extraction, according to the rule of majority, corresponding one bit of watermark information will be extracted from each sub-block. Experimental results show that the scheme has good invisibility and robustness against the attacks of JPEG compression, noise, filtering, scaling and cropping, and can achieve blind watermark extraction as well.

KeywordsDigital watermarkingContourlet transformQR decompositionRobustnessBlind watermarking

收稿日期：2015-01-28。公安部技术研究计划项目(2014JSYJA0 16)。刘海，硕士，主研领域：图像处理，数字水印。陈军，教授。

中图分类号TP391

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.073