基于分布式图计算框架的好友推荐算法研究

赵马沙　周　薇　张　豪　韩冀中

1(中国科学院信息工程研究所信息智能处理技术研究室　北京 100093)2(中国科学院大学　北京 100049)3(重庆邮电大学通信与信息工程学院　重庆 400065)



基于分布式图计算框架的好友推荐算法研究

赵马沙1,2周薇1,2张豪3韩冀中1

1(中国科学院信息工程研究所信息智能处理技术研究室北京 100093)2(中国科学院大学北京 100049)3(重庆邮电大学通信与信息工程学院重庆 400065)

摘要随着社交网络的兴起与发展，用户数目规模呈现出指数级增长的趋势。这些大规模数据里蕴含着许多有价值的信息，挖掘其中有用的信息已经成为学者研究的重点，好友推荐就是数据挖掘里的一个重要应用。为了获得更优的性能、更高的可扩展性，采用分布式平台解决大规模好友推荐成为学术界和工业界的一个发展趋势。目前使用得较广泛的为基于MapReduce框架的好友推荐算法，该方法有较高的可扩展性，但是受限于MapReduce低效的中间数据传输，存在性能缺陷。针对上述问题，提出一种基于分布式图计算框架的好友推荐算法。最后，在多个真实的社交网络数据集上评测了该方法。实验结果表明，该方法要优于业界先进的好友推荐算法，在准确率相当的情况下，性能大约为其他算法的7倍。

关键词好友推荐分布式图计算框架随机游走

0引言

随着Web2.0的出现及兴起，社交网络得到了蓬勃发展，用户数越来越多。2014年一月份的调查表明[1]，Twitter[2]每月的平均活跃用户人数高达2.41亿。2014年5月，QQ空间官方声称其每月的平均活跃用户高1.2亿。这些大规模数据里蕴藏着许多潜在的有价值信息，而挖掘其中的有用信息已经成为业界学者的一个研究重点。其中好友推荐[3]就是数据挖掘[4]的一个非常重要的应用，目前已经被广泛地应用在各类社交网站上。

目前的好友推荐算法主要分为两种[5]，一种是基于局部信息的，比如已经被广泛应用于社交网络的二度人脉(好友的好友)好友推荐。这种基于局部信息的算法计算复杂度低，运行消耗的时间少，但因其利用的信息量少，所以准确率不高。第二种是基于全局信息的好友推荐算法，算法通常会侦测整个社会图的所有路径结构，由于其利用了更多的信息，所以推荐结果更加准确。但是对于大规模的在线社交网络来说，这类方法的计算成本相当高，不适用实时推荐。

针对以上缺陷，有学者提出了基于局部随机游走的好友推荐算法[6]。它根据“小世界”理论[7]，随机游走有限范围内的所有路径，为用户提供了既快速又准确的朋友推荐。

为了应对日益增长的社交网络数据，分布式好友推荐算法也得到了研究学者的青睐。目前使用得较为广泛的是基于MapReduce的大规模好友推荐算法[8]。该算法拥有较高的可扩展性，能应对日益增长的社交网络数据。但由于MapReduce框架中间数据的持久化机制，在其上实现的好友推荐算法性能较低。

针对以上问题，本文提出一种基于分布式图计算框架的好友推荐方法。该方法结合了局部随机游走和分布式图计算框架，实现了好友推荐迭代计算，中间数据采用消息传递的模式，减少了数据持久化的代价。最后，在分布式集群下评测了本文提出的方法，使用多个真实的大规模社交网络公开数据集。实验结果表明，该方法在性能上比单机的好友推荐算法提高了4倍，比基于MapReduce框架的算法提升了7倍，并且该算法具有较高的可扩展性，随着集群规模的增长成正比增长。

1相关工作

好友推荐算法有很多，社会学中的同质性理论认为，拥有相同爱好的人更可能成为朋友，所以很多社交平台通过用户属性的相似度来推荐好友[9,10]。比如百度利用用户的爱好等属性推荐朋友。

还有一种方法就是利用好友关系的网络拓扑图[11]，主要有两类：一类是基于社会网络结构的局部特性，比如二度人脉FOAF(FriendofaFriend)的方法[12]。它基于这样的现象：如果两个人有很多共同的朋友，那么他们在将来就很有可能成为朋友。由于FOAF的简单高效，所以Facebook、腾讯QQ等均采用它为用户推荐潜在好友。但是，这种基于网络局部特性的方法由于利用的信息不充分，得到的结果往往不是很准确。另一类方法是基于社会网络的全局特性，探索社会网络图中的所有路径结构，比如经典的Google网页排序算法PageRank[13]，利用了整个图结构的信息。虽然这种算法提高了结果的准确性，但是在现实的社交网络中，用户数目通常是上百万、千万甚至是亿，运行这种算法成本太大，消耗的时间太多，也不适合应用在实时推荐上。

为了解决上述问题，有学者提出了一个基于局部随机游走的好友推荐算法。这个方法考虑了更多的邻居信息，具有更高的准确性；同时比起基于全局的方法，由于无需遍历整个社会图，因此其具有更低的时间复杂度。

上述所有的方法都是为单机而设计的，当社交网络用户数增多，面对复杂的大规模好友推荐时，就会出现计算效率的问题，而且不具有很好的可扩展能力。于是一些学者开始研究可扩展的分布式好友推荐算法，通过集群的计算能力来应对大规模数据带来的挑战。文献[14]提出了基于MapReduce框架的分布式好友推荐方法，该方法采用MapReduce的Key-Value结构实现了二度人脉等好友推荐算法[15]。尽管MapReduce具有较高的可扩展性，但是其低效的中间数据共享方式导致了该方法的性能不高。

2相关背景

2.1BSP模型

大同步并行BSP(BulkSynchronizationParallel)模型是由哈佛大学Valiant和牛津大学BillMcColl提出的并行计算模型。BSP模型是一种包含一个主节点和多个从节点的分布式的模型。每个从节点负责处理图中的一个子图，作业的处理是由迭代的过程组成，每次迭代称为一个超步。超步是在数据处理中的最小计算单位，主要包括三个阶段：并行计算、通信和栅栏同步，如图1所示。

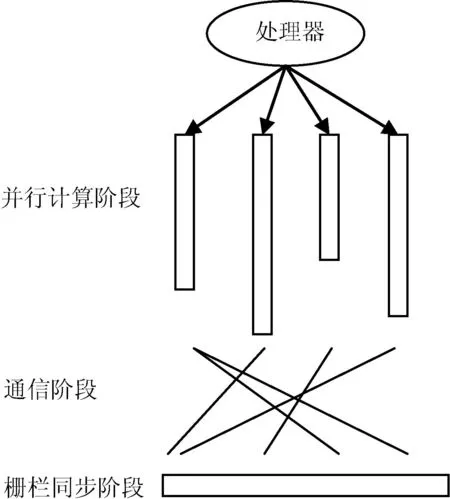
图1　BSP超步的三个阶段

1) 本地计算阶段，每个节点只处理本节点维护的数据。

2) 全局通信阶段，每个节点将本地计算的结果发送给邻居节点。

3) 栅栏同步阶段，等待所有通信行为结束。

在一个确定的超步中，一个从节点只有在上一个超步中接收到所有来自相邻顶点的消息才可以处理这一个顶点。此外，该系统只有所有图顶点都处理完毕之后才进行下一个超步。

目前，很多公司已经开发了许多基于BSP模型的图数据处理系统，最著名的就是Google发明的Pregel[16]。Pregel是一种面向图算法的分布式编程框架，采用迭代的计算模型。在每一轮，每个顶点处理上一轮收到的消息，并给相邻顶点发消息，更新自身状态和拓扑结构(出、入边)等。类似的还有Apache的Hama[17]，它是Hadoop[18]生态系统中的一个子项目，兼容很多Hadoop的分布式存储系统，如HDFS、HBase等。

由于Pregel并非开源，我们基于Pregel的思想实现了BSP图计算框架[19]，本文的实验也是运行在该框架上。与Pregel类似，BSP图计算框架首先将图分割为顶点不相交的子图并将各个子图分配到计算节点上，BSP图计算框架的计算过程基于BSP模型实现。计算被分为多个超步，每一超步中各个计算节点依次调用各个顶点的更新函数。在顶点更新函数中，每个顶点可以根据所收到的上一轮的消息更新该顶点的状态并产生本轮发送给其他顶点的消息。待所有图顶点均更新完毕且所有消息均已到达目标节点，各计算节点进行栅栏同步并同时进入下一超步。这一过程循环往复直至所运行的算法达到收敛条件。因此，基于BSP框架实现图算法时，主要工作是通过编写顶点状态更新函数来完成的。

2.2基于局部随机游走的好友推荐算法

基于局部随机游走的顶点间相似性是一个在社会图的基础上定义的相似性指标。

首先给出社会图的定义，社会图是一个由顶点集合和边集合构成的社会网络，顶点代表用户，边代表用户之间的关系，两者之间构成一个图。

正式地，根据图理论定义社会图G=(V，E)，其中V表示顶点集合，也就是用户集合，E表示无向边集合，也就是用户之间的关系。仅当两个顶点vi、vj间的无向边(vi，vj)∈E时，vj(vi)被称为vi(vj)的邻接。这样社会图能够表示为邻接矩阵A=(aij)∈E，如果vi和vj为朋友，则aij=1，否则为0。

(1)

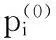
20世纪60年代，美国著名社会心理学家Milgram提出了“小世界”理论。理论指出：你和任何一个陌生人之间所间隔的人不会超过五个，也就是说，最多通过五个中间人你就能够认识任何一个陌生人。这个理论已经被应用到了很多的领域，局部随机游走算法的思想就是根据“小世界”假说，在社会图上进行有限长度的随机游走，而不是针对整个社会图进行全局地遍历[20]。

(2)

其中L代表图顶点vi、vj之间随机游走的路径长度，根据“小世界”理论，可取2到6之间的整数，E为社会图中边的总数目，Γ(j)是顶点vj的度，代表顶点的流行度，流行度指数β是一个可变参数，调节顶点vj的流行度对相似度的影响，实验证明β取0.5时得出的结果最理想。

学者还通过大量的实验证明，在准确性上，基于局部随机游走的好友推荐算法高于基于二度好友的方法，甚至高于基于全局的推荐算法。基于全局的推荐算法虽然对社会网络进行全局遍历，但其没有充分地捕获图中顶点(用户)的局部信息[21]。而基于局部随机游走的好友推荐算法根据“小世界”假设，更加注重顶点(用户)附近邻居的作用，充分利用了用户局部信息，所以它的准确性能够高于基于全局的好友推荐方法。在性能上，基于局部随机游走的好友推荐算法远高于基于全局的推荐算法。

3基于图计算框架的好友推荐算法

本节描述了本文提出的一种基于分布式图计算框架的好友推荐方法。首先介绍该方法并行化的原理，然后以算法的形式详细介绍了图计算迭代完成好友推荐的3个阶段：初始化阶段、迭代阶段以及结束阶段。

3.1原理

首先分析式(1)，转移概率矩阵Q就是图中顶点之间互相转移的概率。如图2所示，aij代表顶点i到顶点j的转移概率，也就是下一步从顶点i到顶点j的概率。矩阵中每一行代表某一个顶点到其他顶点的转移概率，根据矩阵元素的计算公式，可以得到结论。如果顶点i和顶点j无边，转移概率则为0，如果有边，转移概率就是顶点i包含的边的倒数。

图2概率转移矩阵Q

式(1)中出现了Q的转置，转置矩阵如图3所示。

图3概率转移矩阵Q的转置

从图3可以看出，转置后的矩阵中，每一行代表其他顶点到该顶点的转移概率。

[pi0pi1pi2…pin]

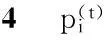
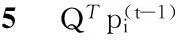
图5是一个列向量，每一个元素是由n个加数相加得到。对每个加数ajk×pij，分析其意义，pij为顶点i经过t-1步到达顶点j的概率，ajk为顶点j到达顶点k的概率，两者相乘即为顶点i经过t步到达顶点k的一部分概率，而所有的加数相加就代表顶点i经过t步到达顶点k的概率。通过这种形式化的分析，我们就可以理解式(1)了。

3.2算法

在BSP上实现分布式的局部随机游走算法分为3个阶段，分别为初始化阶段、迭代阶段和结束阶段：

1) 初始化阶段：根据输入的图数据文件，遍历文件中的每一行，在BSP中生成顶点对象，然后记录每个顶点的边。

算法1初始化图数据

输入：图数据文件file

1：foreachlineinfiledo

2：vertex←createVertex(line)

//line是文件file的每一行数据，vertex是BSP框架中的顶点对象

3：edges←getEdges(vertex)

//edges是存储顶点所有的边

4：endforeach

5:return

2) 迭代阶段：BSP框架控制每个顶点运行该阶段，首先顶点会接受每一条边发过来的消息，得到其中的值。然后计算p值，如果迭代次数没有达到指定次数，则继续发消息，再次迭代，如果达到指定次数，则停止。

算法2迭代阶段

输入：顶点vertex，顶点的边edges，迭代的次数turn

1：foreachedgeinedgesdo

2：dstVertex←getDstVertex(edge)

//dstVertex是目标顶点

3：value←getMessage(dstVertex)

//value是边的权值

4：values.add(value)

5：endforeach

6：p←calculate(vertex,value)

7：ps.add(p)

8：ifturn<=STEPthen

//如果迭代次数小于STEP，继续发消息

9：foreachedgeinedgesdo

10：dstVertex←getDstVertex(edge)

11：sendMessage(dstVertex,p)

//把p值发给每条边

12：values.add(value)

13：endforeach

14：elsehalt()

3) 结束阶段：每个顶点计算得到p值后，BSP框架计算出每个顶点和目标顶点的相似度sin，然后把所有的sin存储sins集合中，最后集合汇总对所有的sin进行排序，最后按照相似度从大到小输出。

算法3结束阶段

输入：各顶点的ps

输出：各顶点的相似度，从大到小输出

1：foreachvertexdo

2：sin←getSin(ps)

//sin就是相似度的值

3：sins.add(sin)

//sins存储所有顶点的相似度

4：endforeach

5：printsort(sins)

//输出排序的结果

6：return

4实验结果

4.1测试数据集和实验环境

为了评测本文方法的有效性，本文选取两个好友推荐对比系：单机的局部随机游走算法和基于MapReduce的二度人脉好友推荐算法。并在多个真实公开的数据集上做了评测实验，和单机的局部随机游走算法比较。一方面证明本文提出的分布式算法是正确的，另一方面说明分布式的算法能带来很大的性能提升，从而可以应付日益增长的大数据集带来的挑战。和如今被很多公司广泛用到的二度人脉算法比较，说明本文提出的算法比现在流行的算法拥有更高的性能，可以在实际中应用。实验环境是由4台主机组成的集群，具体硬件配置参数如表1所示。

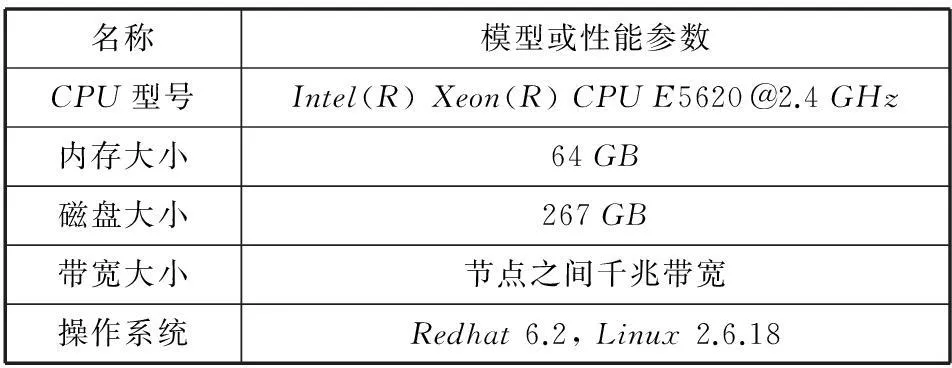
表1　实验环境

在数据集的选取上，本着真实公开和全面的原则，选择了5个不同大小的数据，如表2所示。所有的数据来源各社交网站里，从law.di.unimi.it/datasets.php下载，由WebGraph和LLPprojects提供。这5个数据集的规模是从小到大增长的，很好地说明了本文提出的方法拥有很好的扩展性。其次从数据集中顶点的平均边数也可以看出每个图的稀疏程度不同，说明本文提出的方法适用面广泛。

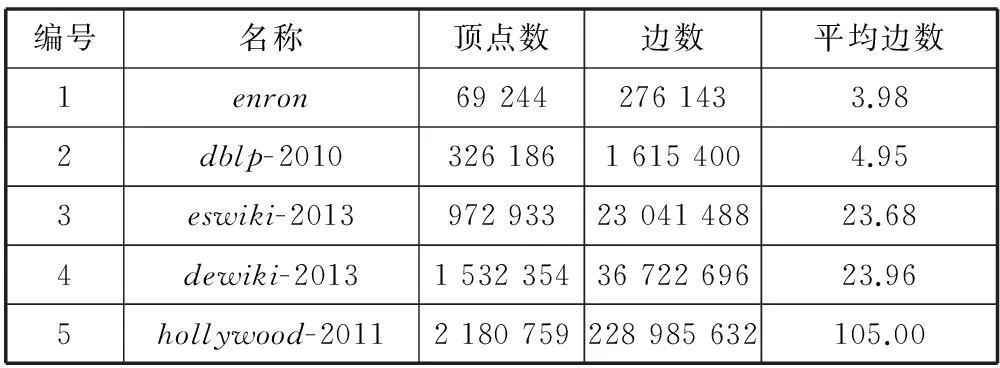
表2　实验数据集

4.2和单机的局部随机游走算法比较

首先我们对分布式算法和单机算法的结果进行了比较，实验表明两种算法中相同顶点的相似度都是一样的，所以局部随机游走算法的分布式版本是正确的。

接下来，我们测试了单机算法和分布式算法运行的时间，数据如表3所示。

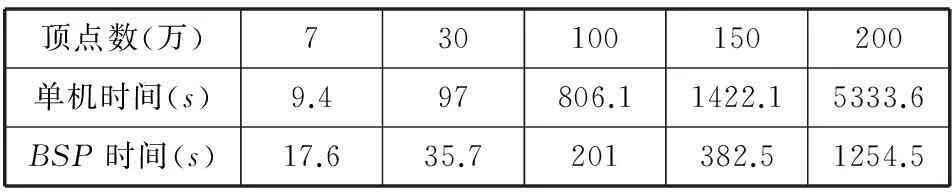
表3　分布式和单机时间对比

由表3得出的时间对比图如图6所示，横坐标是测试数据集中顶点的个数(大致)，万为单位，纵坐标是算法运行的时间，秒为单位。

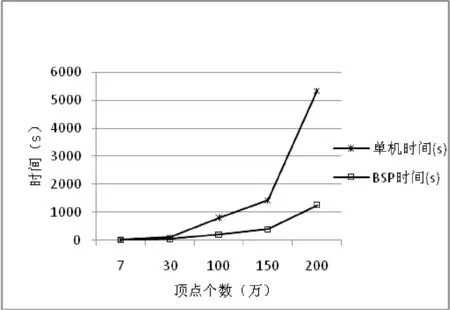
图6　单机和并行算法时间对比图

由图或者表中的数据可以看出，数据量小的时候，分布式算法时间要消耗得更多一些，这是因为并行框架本身要消耗资源和时间，并行带来的性能还没有弥补框架损失的性能。但随着数据集的增大，很明显，分布式的时间比单机版本消耗的时间要少，性能大约提升了四倍，而且性能的提升程度和集群的大小是成正比的。

4.3和MapReduce的二度人脉算法比较

在分布式好友推荐算法中，基于MapReduce的二度人脉好友推荐算法使用得较广泛，Facebook和Hi5等OSNs就使用了该方法进行好友推荐，来自于Facebook的数据科学家LarsBackstrom在eswc2011的报告[22]中介绍了他们是如何利用二度人脉的算法来为用户推荐朋友。下面就BSP上的局部随机游走算法和MapReduce上的二度人脉算法进行比较。首先看两个算法的推荐效果。采用MeanReciprocalRank(MRR)值作为测试指标，在原来的数据图中删除某顶点的10个好友，然后分别用这两个算法试图把删去的10个好友推荐回来，比较这十个好友的MRR值，结果如表4所示。

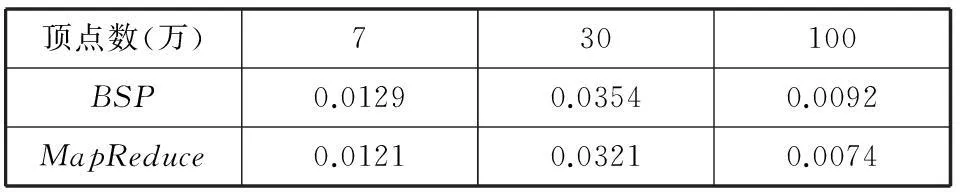
表4　MRR值对比

由于数据量很大，一个顶点的边有很多，所以得到的MRR值非常小。由表4可以看出，BSP的MRR值比MapReduce的MRR值要大，可以得出结论，BSP上的局部随机游走算法的推荐是更准确的。

接下来，比较两者的计算时间，数据如表5所示。

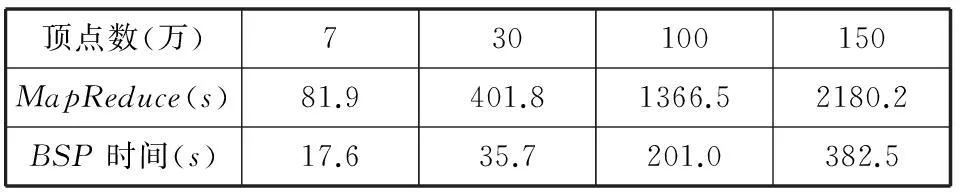
表5　两个并行算法时间对比

图7是表5中数据的折线图显示，横坐标是测试数据集顶点的个数，单位为万，纵坐标是算法运行的时间，单位为秒。

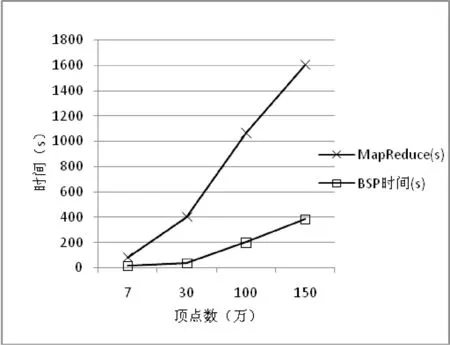
图7　单机和并行算法时间对比图

由图7可以看出MapReduce上的二度人脉的性能远远不如BSP上的局部随机游走算法的性能，主要原因是并行框架的差异，BSP适合迭代图数据计算，中间消息采用消息传递，而不是通过文件系统存储中间结果。而MapReduce框架的启动代价比较大，并且中间的结果是存储在本地磁盘中，从而每次计算会产生大量的IO操作，所以抑制了性能。

5结语

本文首先提出了一种基于分布式图计算框架的好友推荐方法，然后通过大量的实验证明了该方法的高效性和可扩展性。实验中，首先和单机的局部随机游走算法进行了比较，证明了分布式的算法能够带来很大的性能提升，从而可以通过增加普通集群的方式来应付大数据带来的挑战。接着又和现在流行的二度人脉算法进行了比较，证明了本文提出的算法具有很高的应用价值。为了进一步提高本文方法的适用面，未来我们的工作主要集中在优化好友推荐算法上。

参考文献

[1]SocialNetworkService[EB/OL].http://newsroom.fb.com/Key-Facts.

[2]HaewoonKwak,ChanghyunLee,HosungPark,etal.WhatisTwitter,asocialnetworkornewsmedia?[C]//Proceedingsofthe19thInternationalConferenceonWorldWideWeb,2010:591-600.

[3]IdoGuy,InbalRonen,EricWilcox.Doyouknow?:recommendingpeopletoinviteintoyoursocialnetwork[C]//Proceedingsofthe14thinternationalconferenceonIntelligentuserinterfaces,February08-11,2009:77-86.

[4]MarkHall,EibeFrank,GeoffreyHolmes,etal.Thewekadataminingsoftware:anupdate[J].ACMSIGKDDexplorationsnewsletter,2009,11(1):10-18.

[5] 王兵辉.社交网络中潜在好友推荐算法研究[D].云南大学,2013.

[6] 俞琰,邱广华.基于局部随机游走的在线社交网络朋友推荐算法[J].系统工程,2013,31(2):47-54.

[7] 佟婷婷,宋艺.小世界理论及其在Internet中的应用[J].企业技术开发,2010,29(1):26-27.

[8] 杨婷.基于MapReduce的好友推荐系统的研究与实现[D].北京邮电大学,2013.

[9] 杨长春,杨晶,丁虹.一种新的新浪微博好友推荐算法[J].计算机应用与软件,2014,31(7):255-258,274.

[10] 于海群,刘万军,邱云飞.基于用户偏好的社会网络二级人脉推荐研究[J].计算机应用与软件,2012,29(4):39-43.

[11]SilvaNB,TsangIR,CavalcantiGDC,etal.Agraph-basedfriendrecommendationsystemusinggeneticalgorithm[C]//Proceedingsof6thIEEEWorldCongressonComputationalIntelligence.Piscataway:IEEEPress,2010:233-239.

[12] 张龙昌,刘志晗,王攀,等.基于FOAF的分布式移动SNS应用[J].电信科学,2010,26(5):88-92.

[13] 平卫芳.Web数据挖掘中PageRank算法的研究与改进[D].华东理工大学,2014.

[14] 贺超波,汤庸,陈国华,等.面向大规模社交网络的潜在好友推荐方法[J].合肥工业大学学报:自然科学版,2013,36(4):420-424.

[15]MapReduce上实现二度人脉好友推荐算法[EB/OL].http://www.datalab.sinaapp.com/?=192.

[16] 张杰.PyGel:基于DPark的分布式图计算引擎的研究与实现[D].华南理工大学,2013.

[17] 蔡大威.基于Hadoop和Hama平台的并行算法研究[D].浙江大学,2013.

[18] 朱珠.基于Hadoop的海量数据处理模型研究和应用[D].北京邮电大学,2008.

[19]WeiZhou,BoLi,ZhangZhang,etal.Arbor:EfficientLarge-ScaleGraphDataComputingModel[C]//Proceedingsofthe15thIEEEInternationalConferenceonHighPerformanceComputingandCommunications,2013:300-307.

[20] 李金枝.基于RWR的图像分割算法研究[D].重庆大学,2010.

[21]PapadimitriouA,SyseonidisP,ManolopoulosY.Fastandaccuratelinkpredictioninsocialnetworkingsystems[J].JournalofSystemandSoftware,2012,85(9):2119-2132.

[22]DealingwithstructuredandunstructureddataatFacebook[EB/OL].http://videolectures.net/eswc2011_backstrom_facebook/.

STUDY ON A FRIEND RECOMMENDATION ALGORITHM BASED ON DISTRIBUTEDGRAPHCOMPUTINGFRAMEWORK

Zhao Masha1,2Zhou Wei1,2Zhang Hao3Han Jizhong1

1(Institute of Information Engineering,Chinese Academy of Science,Beijing 100093,China)2(University of Chinese Academy of Science,Beijing 100049,China)3(School of Communication and Information Engineering,Chongqing University of Posts and Telecommunications,Chongqing 400065,China)

AbstractWith the rise and development of social networking sites, the user number show a growth trend in exponential level, in these massive data there contains a lot of valuable information, and to mine the useful information has become the focus of the scholars in their studies. The friend recommendation algorithm is one of the most important applications in data mining. To acquire better performance and higher scalability, it becomes a developing trend in both the academia and the industry to use a distributed platform in solving the large-scale friend recommendation. Currently, the friend recommendation algorithm based on MapReduce framework has been widely used because of its high scalability. However, the inefficient transmission of the intermediate data of MapReduce results in the performance deficiencies. To solve these problems, the paper proposes a distributed graph computing framework-based friend recommendation algorithm. In end of the paper, we give the evaluation of the proposed algorithm on a couple of real social network datasets, and the experimental results show that it is superior to the advanced friend recommendation algorithms of the industry, and its performance is about seven times than that of other algorithms under the circumstance of similar accuracy.

KeywordsFriend recommendationDistributed graph computing frameworkRandom walk

收稿日期：2014-10-09。国家自然科学基金项目(60903047)；国家高技术研究发展计划项目(2012AA01A401，2013AA013204)；中国科学院先导专项(XDA06030200)。赵马沙，硕士生，主研领域：大规模数据处理。周薇，博士生。张豪，硕士生。韩冀中，教授级高工。

中图分类号TP3

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.008