基于符号执行与混合约束求解的测试用例生成研究

周海将　吴军华

(南京工业大学计算机科学与技术系　江苏 南京 210009)



基于符号执行与混合约束求解的测试用例生成研究

周海将吴军华

(南京工业大学计算机科学与技术系江苏 南京 210009)

摘要由于现有基于符号执行的测试用例生成方法无法对关于字符串的测试用例生成提供有效支持，因此提出并实现了基于符号执行与混合约束求解测试用例自动化生成方法。该方法利用模型检测软件对被测软件源代码进行符号执行，生成关于字符串与数值的混合约束集,利用字符串-数值约束求解器对约束集进行求解，最终根据求解结果生成软件测试用例与不可达路径。实验结果表明，该方法较好地支持了关于字符串测试用例生成，且具有良好的效率与准确性。

关键词测试用例生成符号执行技术混合约束求解字符串

0引言

随着软件业的不断发展，主流软件中字符串操作的占比越来越大[1]。例如Web软件中后台逻辑处理部分通常需要与数据库进行交互，其中SQL语句的动态生成主要通过字符串操作完成。此外，前端界面用于显示的字符串变量与常量基本通过字符串操作动态地生成。而软件测试是保证软件质量的重要手段，由于早期的传统软件测试方法主要针对数值与逻辑计算，对于字符串变量和字符串操作不能有效的支持，因此关于字符串的测试用例生成技术逐渐成为国内外的研究热点之一[2]。

1研究现状

近年来软件测试领域基于符号执行的测试研究成为热点。它是一种静态程序分析技术[3]，主要原理是使用符号变量代替实际值模拟程序的执行，获取相应路径的约束，最终通过约束求解获得测试数据。如今该技术的瓶颈在于约束求解器的效率，尤其缺乏优秀的字符串求解器。关于约束求解技术，根据表示字符串的形式，字符串约束求解器主要分为基于位向量与基于有限状态自动机两种类型。

HAMPI[4]是基于位向量的字符串约束求解器，主要原理是将输入的字符串约束转换为是否为正则语言接受的形式，利用位向量表示，最后利用STP位向量求解器求解约束条件。但仅支持固定长度的字符串约束且不支持数值约束。Kudzu[5]基于位向量，改进了HAMPI，提供了较多字符串操作的支持，并且有限支持数值约束。

文献[2]详细论述了基于有限状态自动机的字符串约束求解器技术。其中Rex[7]基于有限状态机与SMT约束求解器，使用逻辑谓语表示自动机的转换。Rex支持字符串约束与数值约束，但效率很低，远远慢于HAMPI。文献[8]提出一种基于怠惰算法的约束求解技术，利用图表示字符串之间的约束，通过回溯搜索图寻求结果。该技术若有解时，效率很高；若无解则求解时间往往超出可接受范围。此外，该技术只能对字符串操作与正则语言提供有限的支持。

综上所述，要实现基于符号执行软件测试自动化，就应改进约束求解技术的效率与增强适用性。

2符号执行与约束求解

符号执行[3]是一种可靠的程序分析技术，基本原理是：在源代码中，将程序中变量值替换为表示为未知但固定的符号标记，模拟程序执行的过程。符号标记在静态数学意义上用来表示一些未知的但固定的值，一个程序在特定的执行过程中会有与其相关的多个不同的符号标记。主要思想是从控制流图的入口处用符号标记代替具体的输入值来模拟程序符号化的执行过程。一般的软件测试用具体值作为测试用例输入来执行程序，所进行的计算是具体逻辑运算，符号执行使用符号标记来执行程序，所进行的是代数运算，符号执行即一般测试的扩充。符号执行是程序验证和程序测试的折中，一方面它具有普通测试所具有的测试方法，通过运行被测程序验证程序的可靠性；另一方面，符号执行沿着一条路径的一次执行积累的约束条件代表了一大类普通测试的集合，验证程序接受此类输入后是否正确，同时可以发现程序中不可行的路径。

约束问题由三个基本元素组成：变量、变量域与约束。约束求解即在变量域中找到特定变量值使之与各变量之间均满足约束。混合约束问题是传统约束问题的扩展，即变量域为多个，本文分为数值变量域与字符串变量域。约束求解技术主要包括数值法、符号计算法、区间分析法、启发式算法等。

3基于符号执行与混合约束求解的测试用例生成技术

3.1符号执行框架

本文提出了一个基于符号执行技术与混合约束求解的测试用例自动化生成方法框架，总体来说包括两个部分：符号执行生成约束部分；对约束集求解得到测试输入与不可达路径部分。主要步骤为：

(1) 将源程序进行扩展，利用符号执行工具对已扩展的源代码进行符号执行，遍历源程序的每个路径，生成每个与程序终点相对应的路径条件。路径条件定义为与该程序终点对应的约束。这样的过程最后得到的就是路径条件集合，即约束条件集合。

(2) 利用约束求解方法对约束条件集合进行约束求解，得到关于每个程序终点的约束的具体值，即程序测试输入。若约束求解无解，即程序终点不可达，说明该路径是错误的，返回该错误路径。符号执行框架的结构如图1所示。

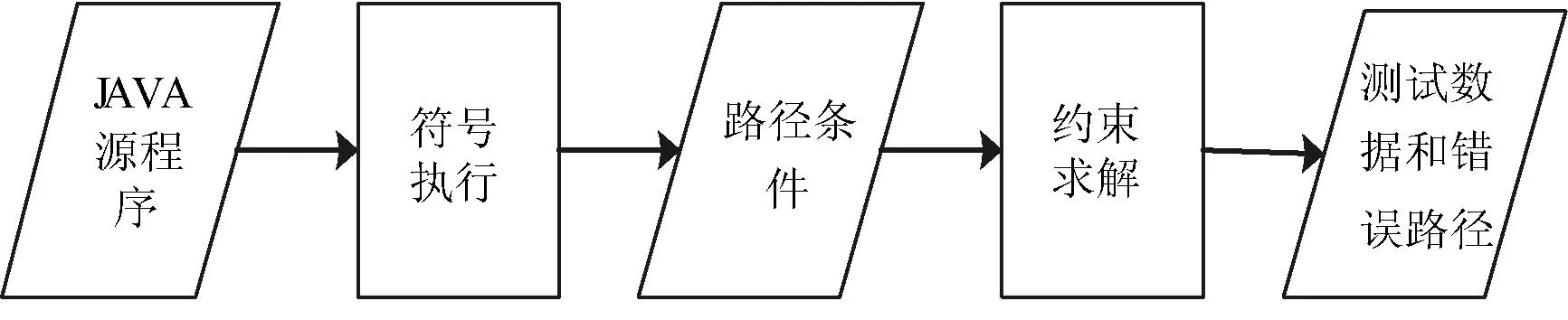
图1　基于符号执行与混合约束求解测试用例生成框架

本文对基于符号执行与混合约束求解测试用例生成框架给出以下定义:

定义 1定义执行该路径得到的路径条件为PC(Path Condition)，PC积累了该路径每一条语句执行必须满足的约束。不可达路径的执行路径定义为PU。

定义2约束集C：定义由对源程序进行符号执行得到的路径集合为C{c1,….,ci,….,cn},称C为约束条件集合，其中ci表示某个具体的路径条件表达式，n为约束条件的总数。

定义3若是关于数值的路径条件，定义为数值约束PCN；若是关于字符串的约束，定义为字符串约束PCS；若PC中既包含数值约束又包含字符串约束，称该PC为混合约束条件PCH，对于混合约束条件集合为CH。

定义4由PCN求解得到的值为关于数值约束条件的测试输入，定义为TN;由PCS求解得到的值为关于字符串约束条件的测试输入，定义为TS;相应的TN与TS的集合即关于该执行路径的测试输入T。

定义5由对约束条件集合进行求解的过程定义为S，其中S的输入是约束条件集合，输出为测试输入集合与不可达路径条件。表达式为：

S(C)=TANDPU

其中C={c1,…,ci,…,cN};T={T1,…，Ti,…，TN}，Ti=TNiANDTSi。

3.2路径条件生成

本文将通过图2的例子详细论述符号执行的过程。图2表示的是根据字符串取值的不同采取不同处理，目的是对字符串进行辨识以确定S的含义，并决定采取哪些方法处理S。

图2　路径条件的分支树

如图2所示，PC0表示的是符号执行的起点，Path1-Path6表示的是符号路径的终点。符号L(q)代表字符串q的长度。符号执行过程中，首先检测输入字符串是否以负号为开头，即检测字符串s代表的是否为负数；接着检测字符串是否符合正则表示式的格式；然后检测字符串s中是否含有逗号，若无逗号，字符串s将被转换为长精度类型，否则将s中逗号后面的数字赋值整型变量x;最后检测x是否小于100。这个代码在一般的Web程序中比较常见，首先对输入字符串进行格式检测，接着将字符串转换为数字，最终在分支中对字符串进行处理。在每个路径终点都生成了约束条件的交集，即通过符号执行得到的约束条件集合C，其中C中元素为：

c1={s.charAt(0)==’-’}

c2={ s.charAt(0)==’-’,s.matches(“-d+,d{3}”)}

c3={s.charAt(0)==’-’,s.notmatches(“-d+,d{3}”,s.notCtains(“,”),i==-1,f==VOF(s),f1==(f/102),round(f1/3)=dl}

c4={s.charAt(0)==’-’,s.notmatches(“-d+,d{3}”,s.notCtains(“,”),i==-1,f==VOF(s),f1==(f/102),round(f1/3)≠dl}

c5={s.charAt(0)==’-’,s.notmatches(“-d+,d{3}”,s.subString(i,i+1)==”,”sl=s.substring(i+1),VOF(sl)>=100 }

c6={s.charAt(0)==’-’,s.notmatches(“-d+,d{3}”,s.subString(i,i+1)==”,”sl=s.substring(i+1),VOF(sl)<100 }

在下一步中通过对C进行约束求解，则可以生成测试数据与不可达路径。由于C中的元素ci既包含PCN又包含PCS，因此，约束求解器就需要具有对PCN和PCS两种约束条件的求解能力。当前的约束求解算法对字符串约束不能提供有效支持，对此本文提出并实现了数值—字符串混合约束求解器[9]。

3.3混合约束求解算法

混合约束集合包含数值约束与字符串约束。本文对此的解决方法为：通过将两种约束集进行分离，运用不同的约束求解器进行处理。数值约束条件选用已有的Coral[10]方法和Yices[11]方法处理，其中线性数值约束使用Yices方法处理，简单非线性数值约束使用Coral方法处理。对于字符串约束条件使用本文设计的基于有限状态机(FSM)约束求解器。具体算法为：

步骤1初始化约束求解器。加载由符号执行步骤得到的约束条件集合CH。对CH中的所有元素ci遍历执行以下步骤。

步骤2利用Coral与Yices数值约束求解器对ci中的PN部分进行求解，若无解则输出该执行路径，并退出；若有解，保存Ts并执行下一步。

步骤3将CH中的Cs部分加载到求解器中，并对其进行字符串求解。若有解则输出Ts与Tn。即该执行路径的测试输入；若无解，执行以下步骤。

步骤4首先判断求解时间是否超出限制，若超出则放弃，返回求解时间并退出；反之，根据RULE库替换可以替换的字符串约束条件为相应的数值约束条件，转到步骤1循环。

在算法中提到的RULE库是为了提高混合约束条件求解效率而增加的。主要实现的原理:字符串约束部分可以转换为数值约束，数值约束求解效率一般优于字符串约束期间效率，实现部分数值约束与字符串约束互相的转换将提高求解效率。

3.4字符串约束求解改进

本文使用有限状态机(FSM)表示一个符号字符串变量，即所有变量可能的取值组成了可以被这个FSM识别的语言。实现是基于文献[12]提出的自动机。FSM的转换(边)拥有一个范围取值。当一个自动机求精时，不仅需要改变结点和边，边上的额外取值范围也会变化。例如图3表示的是接受正则表达式“-d+,d{3}”的自动机。

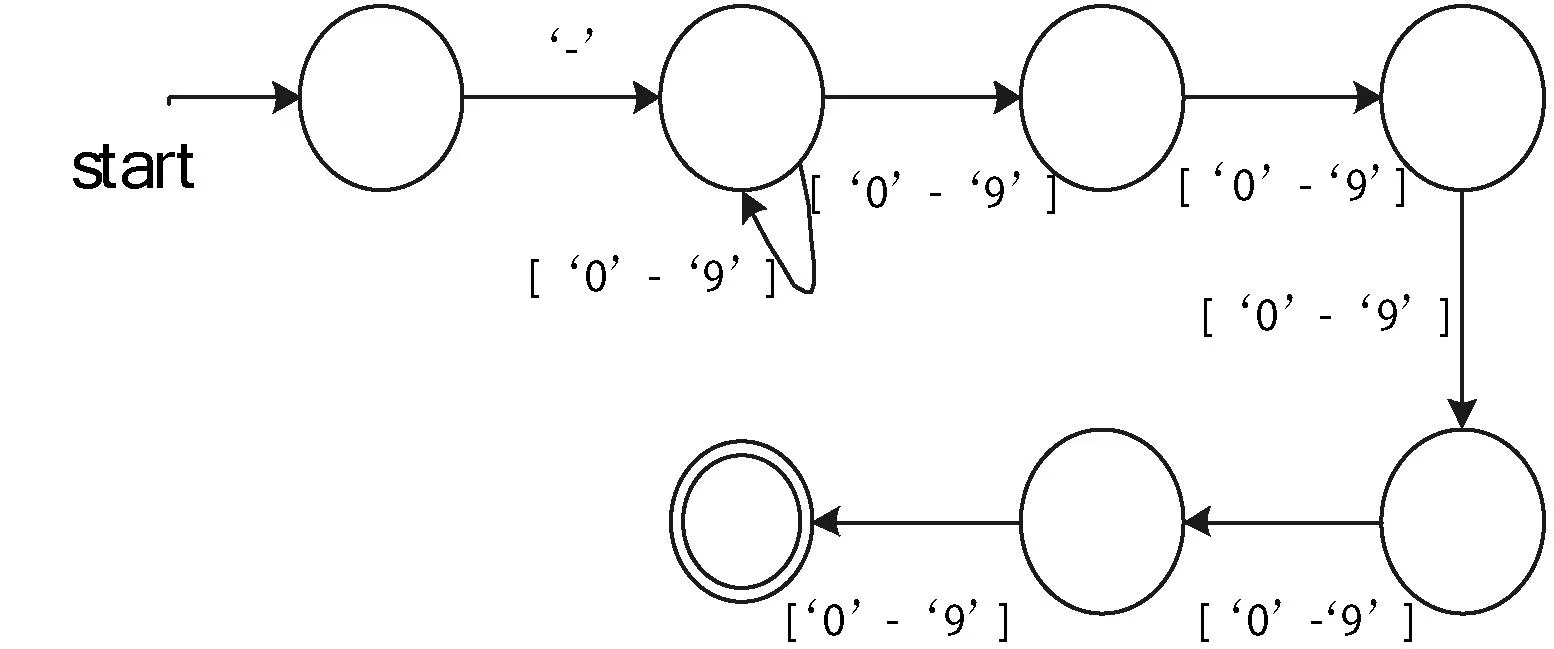
图3　接受-d+,d{3}的自动机

本文通过使用有限状态自动机来实现字符串的操作。例如，字符串s1和字符串s2的连接操作转换为s2的自动机附加到s1自动机的操作。该自动机支持了很多的字符串操作，但是因为其设计是用于静态分析，本文扩展该自动机不支持的字符串操作。例如，substring(2,4)方法的操作返回的是从索引位置2到索引位置4的子字符串，如图4所示。基本方法是：首先从开始状态转移两个步骤；然后将访问到的节点作为开始节点；接着将从开始节点两步转换中所有的状态作为接受状态；最后，我们交互该自动机并接受所有长度为2的自动机用来得到最终的自动机版本。除此之外还有其他需要扩展，比如替换字符与替换子字符串等。

图4　在自动机上操作substring(2,4)操作

字符串约束描述的是字符串之间的关系。FSM并不直接对字符串约束求解，因此需要根据字符串约束加强对字符串的求精。这个过程包括：(1)自动机求精；(2)不动点计算；(3)优化收敛速度。例如，对于s.charAt(0)=’-’约束，将字符串s与接收首字符为负号的自动机交互。后来，因为字符串s的部分通过parseInt方法转换为整型变量，将字符串s的该部分与建模所有有效整数交互；同样需要对字符串s的根据更新部分对字符串s进行求精。例如，将字符串s的自动机与以某种形式结尾部分的自动机交互。这部分工作将一直进行，直到没有什么求精是可能的，并且得到不动点，即得到一个可能的字符串值。

本文通过RULE库来实现字符串约束与数值约束之间的互相转换，因此字符串约束和数值约束对于共享的符号变量取值必须一致，即共享的符号变量在数值约束与字符串约束中的值相同。在符号变量同步的过程中，数值约束求解器N会给出一些候选值，提交给字符约束求解器S判断该符号变量值是否冲突。若无冲突，则符号变量取值被S和N都接受；否则S会返回N引起冲突的约束变量值，请求N提交其他候选符号变量取值。接着N取消冲突的符号变量值，使用启发式算法重新搜索另一个有效赋值，继续以上步骤。在交互的过程中只有共享变量的具体值可以从N提交到S，N也可以理解一些字符串冲突，并传递给S。例如，数值约束s.length()>5使相应的自动机应该与接受长度大于5的自动机交互。

在迭代过程中，我们将字符串约束求解器[14，15]和数值约束求解器得到的约束交换，这样就可以提高收敛速度。例如，对于字符串约束s1=s2.trim()，数值约束求解器会给出一个数值约束给出L(s1)<=L(s2)，其中L()方法返回的是字符串对象的长度。

在方法中，类似上例的交互约束由RULE库建模，RULE库包含一般Java程序常见的交互规则，表1展示了该库的部分规则。

表1　RULE库中部分RULE规则

续表1

为了解释数值与字符串约束迭代求解的过程，对于图2中的path 4,下面给出了path 4的路径条件，包含了已经增加的额外的约束。为了对该约束求解，数值约束求解器将得到一组有效的数值变量赋值，L(s)=2,L(s1)=1,i=0,x=100。然后将这组赋值提交给字符串约束求解器。但是因为x=parseInt(s1)条件不满足，所以字符串求解器没有找到有效赋值。这就要求N进行重新计算直到s1的长度大于等于3，或者求解器利用RULE库从“x=parseInt(s1) ^ 》100”得到一个额外的L(s1)>=3约束。此外从“s1 = s.substring(i+1)”得到L(s)>=L(s1)。有了额外的约束，求解器可以很快得到新的一组有效变量赋值，例如s=“-,100”, s1=“100”, i=1,x=100。

NumericString

(1 : L(s) > 0)s:charAt[0] = `-’

(3 : i + 1 + L(s1) = L(s))s1 = s.substring(i + 1)

(4 : L(s1) > 0)x = parseInt(s1)

i=≠-1 ^ x》 100┐(s.matches(- d+,d{3}))

当字符串约束求解器S不能得到一个有效赋值时，额外的约束被传递给数值约束求解器并始新的迭代计算。最终，混合约束迭代求解器可以得到一个有效的解决。

在符号执行得到的混合约束可能包含非线性数值约束条件，对非线性约束求解，正常的处理不仅效率不高，而且容易导致约束求解失败。对此本文通过将非线性约束条件转换为多个线性约束组合来避免直接求解效果不佳。例如round()方法，该方法的作用是对于给定的浮点数变量返回最接近的整型值。对于round()方法，本文将其转换为“((e-0.5 =x1))^((e-0.5<=x2)^(e+ 0.5 >x2))^(result= (if(e> 0)x1x2 ))”。其中e为实数，x1、x2和result是引进的整型变量，result代表的round(e)的返回值。同样地，将其他的一些约束进行类似的转换，用以处理非线性数值约束。

4实验部分

本文使用的是两个富含字符串操作的Java源程序进行对比试验，使用JPF的符号执行版本[13]对实验样本进行符号执行两个程序的详细情况见表2。由于程序代码量过大，因此仅关注逻辑处理部分，因为这部分代表了程序中最复杂的字符串与数值计算与处理。测试环境为HPPC机-IntelCore2DuoCPUE7500,2.93GHz,2GB;WindowsXPsp3。

表2　实验程序数据

测试中记录生成的是输入符号变量的个数，在程序有效结束状态下生成的测试用例个数，在符号执行中因异常抛出而未执行的路径个数。完成实验的时间、完成实验中迭代的次数见表3所示。最后在符号输入个数为四个时，得到了的测试用例覆盖率达到80%。

表3　程序A的实验结果

由表3可以看出在符号输入个数为4时，得到了的测试用例覆盖率达到80%。综上所述，该技术在合理的时间内能有效自动化地生成测试用例与不可达路径。

为了说明非线性约束求解的有效性，本文使用金融应用程序B进行单元测试。程序B包含很多对Java语言长精度类型的舍入操作。实验对非线性模式开启与否做了多次实验(如表4所示)。当开启非线性模式时，所有生成的路径条件由Yices求解，反之则由Coral求解。可以从表中明显看到，非线性模式下的具有明显优势。

表4　程序B的实验结果

从表3、表4可以看出，本文提出的基于符号执行与混合约束求解技术的测试自动化技术明显优于传统基于符号执行的测试自动化技术。不仅对字符串约束与数值约束提供支持，求解效率也有明显提升。

5结语

本文对符号执行技术、数值—字符串混合约束求解进行了研究，设计并实现了基于符号执行和混合约束求解的自动化测试技术。它能有效提高约束求解效率，并支持字符串约束与数值约束。实验表明，该方法能在可接受的时间范围内生成测试

用例与错误路径。文中的混合约束求解框架还有一些不足与需要改进的算法。混合约束求解算法的效率还存在提高的可能，优化可以采用各个击破的“on-the-fly”技术。此外该方法只能对Java源程序提供支持，以后可以扩展到其他主流编程语言例如C++、C等。

参考文献

[1] 梅宏,王啸吟,张路.字符串分析研究进展[J].软件学报,2012,24(13):37-49.

[2]HooimeijerP,VeanesM.Anevaluationofautomataalgorithmsforstringanalysis[C]//Verification,ModelChecking,andAbstractInterpretation.SpringerBerlinHeidelberg, 2011: 248-262.

[3]KingJC.Symbolicexecutionandprogramtesting[J].CommunicationsoftheACM, 1976, 19(7): 385-394.

[5]SaxenaP,AkhaweD,HannaS,etal.Asymbolicexecutionframeworkforjavascript[C]//SecurityandPrivacy(SP), 2010IEEESymposiumon.IEEE, 2010: 513-528.

[6]VeanesM,DeHalleuxP,TillmannN.Rex:Symbolicregularexpressionexplorer[C]//SoftwareTesting,VerificationandValidation(ICST), 2010ThirdInternationalConferenceon.IEEE, 2010: 498-507.

[7]HooimeijerP,WeimerW.Solvingstringconstraintslazily[C]//ProceedingsoftheIEEE/ACMinternationalconferenceonAutomatedsoftwareengineering.ACM, 2010: 377-386.

[8]ShannonD,GhoshI,RajanS,etal.Efficientsymbolicexecutionofstringsforvalidatingwebapplications[C]//Proceedingsofthe2ndInternationalWorkshoponDefectsinLargeSoftwareSystems:HeldinconjunctionwiththeACMSIGSOFTInternationalSymposiumonSoftwareTestingandAnalysis(ISSTA2009).ACM, 2009: 22-26.

[9]SouzaM,BorgesM,d’AmorimM,etal.CORAL:solvingcomplexconstraintsforsymbolicpathfinder[M]//NASAFormalMethods.SpringerBerlinHeidelberg, 2011: 359-374.

[10]DutertreB,DeMouraL.Theyicessmtsolver[OL]. 2006.Toolpaperathttp://yices.csl.sri.com/tool-paper.pdf.

[11]ChristensenAS,MøllerA,SchwartzbachMI.Preciseanalysisofstringexpressions[M].SpringerBerlinHeidelberg, 2003.

[12]PăsăreanuCS,RungtaN.SymbolicPathFinder:symbolicexecutionofJavabytecode[C]//ProceedingsoftheIEEE/ACMinternationalconferenceonAutomatedsoftwareengineering.ACM, 2010: 179-180.

ON TEST CASE GENERATION BASED ON SYMBOLIC EXECUTION AND HYBRID CONSTRAINT SOLVING

Zhou HaijiangWu Junhua

(Department of Computer Science and Technology, Nanjing Tech University, Nanjing 210009, Jiangsu, China)

AbstractSince current test case generation method based on symbolic execution is unable to provide effective support to the test case generation with regard to character string, therefore we present an automatic test case generation method, which is based on symbolic execution and hybrid constraint solving, and implement it as well. The method uses the model checking software to make symbolic execution on the source code of the software to be tested and generates a mixed constraint set correlated to string and numeral. Then it uses the string-numerical constraints solver to calculate the constraint set. Finally, according to the calculation result it generates the software test case and the infeasible path. Experimental result shows that this method well support the generation of test case in regard to string and has good efficiency and accuracy.

KeywordsTest cases generationSymbolic execution technologyHybrid constraint solvingString

收稿日期：2015-01-30。周海将，硕士，主研领域：软件测试。吴军华，副教授。

中图分类号TP301

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.006