自适应重生鱼群优化算法

易正俊　韦磊鹏　袁玉兴

1(重庆大学数学与统计学院　重庆 401331)2(重庆科技学院数理学院　重庆 401331)



自适应重生鱼群优化算法

易正俊1韦磊鹏1袁玉兴2

1(重庆大学数学与统计学院重庆 401331)2(重庆科技学院数理学院重庆 401331)

摘要针对传统人工鱼群算法求解高维优化问题收敛速度较慢，易于陷入局部最优，提出自适应重生鱼群优化算法。首先在每次迭代过程中，不断地给鱼群注入“新生命”使鱼群得以重生；然后采用正态分布动态调整拥挤度因子的上限值使得算法更贴近于鱼群搜索食物的过程。实验结果表明，改进后的算法既保证收敛速度、增加算法获得全局最优的可能性，又适用于求解大规模的优化问题。其中的两个算例采用改进的鱼群算法进行优化，优化结果与实际具有良好的一致性，说明了改进算法的有效性和实用性。

关键词人工鱼群算法鱼群重生正态分布动态拥挤度因子优化

0引言

人工鱼群算法[1]是李晓磊等人于2002年提出的一种基于动物自治体的新型寻优策略。该算法模拟了自然界中鱼群的觅食、聚群和追尾行为。为了突出人工鱼群算法的全局寻优能力，李晓磊等[2]将人工鱼群算法与遗传算法进行对照，测试后得到其效果更佳，且人工鱼群算法具有集群智能、良好的并行性、参数和初值的鲁棒性强等优点，在工程上已得到广泛使用[3-8]。李亮等[4]于2006年构造了一种两点禁忌寻优算子以避免寻优过程中的迂回搜索，并将其应用到两个复杂土坡的最小安全系数搜索中；方金城等[5]于2011年引入实数编码对鱼群算法进行改进，并将其应用于配送决策问题中;陈安华等[7]于2012年通过定义相似度因子和聚类判别因子，建立了模拟人工鱼群追尾行为的机械故障聚类诊断模型，并将之应用于机械故障特征信息的聚类分析。

通过反复实验发现人工鱼群算法设计思路简单，求解低维优化函数时能够保持较高的精度，且能够较快地获取全局最优解。但我们在实际中遇到的往往是庞大的工程问题，决策变量的维数较高，导致搜索范围的空间复杂度大大增加。这时应用传统的人工鱼群算法很容易陷入局部最优，算法的精度和收敛速度也随之下降。针对以上的不足，本文对人工鱼群算法进行改进，给鱼群注入“新生命”和引入动态拥挤度因子，使其在处理高维优化函数时仍能保持较高的精度。主要思想是在算法迭代过程中，一方面给种群注入“新生命”，丰富了种群的多样性；另一方面通过控制拥挤度因子的值及时地调整鱼群的行为，这样扩大了鱼群的搜索范围，有效地避免算法陷入局部最优。同时，利用仿真实验研究了该方法的有效性。

1自适应重生鱼群优化算法

1.1优化问题的描述

一个优化问题描述如下：

minf(X)X∈S

式中，f(X)表示目标函数，X表示决策变量，S表示可行域。

1.2传统人工鱼群算法的描述

鱼群搜索食物的过程主要包括觅食、聚群和追尾三种行为。觅食表现在当鱼在它的视野范围内发现食物时，则朝该方向游动；聚群是每条鱼在游动过程中尽量地朝邻近伙伴的中心游动，并避免过分拥挤；追尾是指当某条鱼发现该处食物丰富时，其他鱼会快速尾随至此。

在一片水域中，鱼往往能自行或尾随其他鱼找到营养物质比较丰富的地方，因而鱼聚集数目最多的地方往往是水域中营养丰富的地方。人工鱼群智能算法求解最优化问题就是模拟鱼群搜索食物过程的特点，把可行解域看成一片水域，函数在可行解域中的极值点视为水域中鱼群的食物源，函数值视为食物源的食物浓度。然后从构造单条人工鱼开始，通过模拟鱼的觅食、聚群和追尾行为，实现所有人工鱼聚集在食物源中心的附近，再比较相应食物源的浓度值，得出最优食物源，其对应位置的坐标就是最优化问题的解。

鱼的视野范围(记为Visual)是有限的。它在水域中随机游动，若在其视野范围内发现某点的食物浓度大于当前位置的食物浓度，则它会朝食物浓度大的点方向进行移动，移动的步长用step表示。游动到一定的程度，鱼在它的视野范围内可能有多条鱼，此时会产生聚群现象。若每一条鱼当前位置的食物浓度低于视野范围内鱼群的中心位置的浓度，鱼群的拥挤度不是太大，则鱼会朝中心位置移动；同时鱼群中的鱼还会有追尾现象发生，每一条鱼会探索其视野范围内最大食物浓度位置中的鱼，若拥挤度还没有达到极限位置，则鱼会朝最大食物浓度位置游动。

传统的人工鱼群算法经反复实验发现：决策变量X的维数增多时，算法的精度和收敛速度大大地降低了，无法得到全局最优解。实际问题中的许多待优化问题往往是高维的，如资源配送问题、线路设计问题等。因此本文在传统的鱼群算法基础上不断地给鱼群注入新的“生命”，动态修订鱼群拥挤度因子的上限值，更加符合自然界中鱼群的搜索食物的过程。改进后的鱼群算法称为自适应重生鱼群优化算法，适合大规模的优化问题的求解。

1.3反向学习的基本概念

反向学习是智能搜索中的一种方法，已经被证明是随机搜索算法中的一种有效方法[14,15]。下面介绍反向学习中几个基本的概念。

1.3.1反向数

定义1若x∈[a,b]是一维实空间R1中的点，则x的反向数x*=a+b-x。

1.3.1反向点

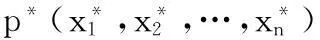
1.4自适应重生鱼群优化算法

1.4.1鱼群重生

鱼群重生是指每次迭代的开始根据上轮迭代所得的N个位置，生成这N个位置分别对应的反向点，重新得到N条人工鱼，给人工鱼注入新的生命，相当于产生新的N个位置。然后把N个位置与上轮迭代所得N个位置的食物浓度进行比较，选取食物浓度最大的前N个位置作为人工鱼的现处位置来参与进化，是对人工鱼的一种更佳的估计。每次迭代通过不断地给人工鱼注入“新生命”，丰富了种群的多样性，人工鱼的搜索范围扩大，跳出局部最优的机会增大，提高了算法获得全局最优的可能性。

1.4.2动态拥挤度因子

拥挤度因子是用来刻画人工鱼群聚集的规模，拥挤度因子δ的设定是避免人工鱼过分地聚集在某个极值点的周围，使得人工鱼能够更广泛的寻优。传统的人工鱼群算法中把δ设定为一个常数，这样设计会影响算法的性能。若δ选取偏小，人工鱼在逼近极值的同时会避免过分拥挤而随机走开，或者受其他人工鱼的排斥作用，不能精确逼近极值点，且导致收敛速度很慢；若δ选取过大，容易陷入局部最优，致使算法出现停滞现象。

现引入动态拥挤度因δk来更加确切地模拟鱼搜索食物的过程。事实上，鱼群在寻找食物开始时，每条鱼在其视野范围内并不拥挤，为更广泛地搜索，避免鱼群过度集中，拥挤度因子δ应该取较小的值；随着鱼群搜索过程的继续，鱼群就会进行聚群和追尾行为，这时鱼的周围变得越来越拥挤，这时为保证最优食物源的周围有更多的鱼，避免因拥挤限制鱼群的聚集，δ应随着搜索的进行而增加。但是迭代后期，鱼群趋于成熟和稳定，鱼群容易陷入局部最优，致使算法停滞不前。这时为了提高人工鱼跳出局部最优的能力，我们应抑制鱼群的聚群和追尾行为，鼓励其进行觅食行为和随机游动，这时我们就要抑制δ的值并适当地降低。鉴于此，随着迭代次数k的不同，拥挤度因子δ也不同，即鱼群算法的拥挤度因子δ应该是迭代次数k的函数δk=δ(k)(δk称为动态拥挤度因子)，且两者的函数关系大致如图1所示。

图1　动态拥挤度因子

由此，鱼群算法中拥挤度因子的上限值δ修正为动态值δk。利用Matlab软件进行拟合，得到其变化规律可以利用正态分布来刻画，且拟合函数为：

其中m代表最大迭代次数。

鱼群算法经过上面两个方面的改进就称为自适应重生鱼群算法，其算法步骤为：

步骤1设定每条人工鱼的视野范围为Visual，移动步长恒定为step，拥挤度因子为δ，最大迭代次数为m。

步骤2初始化鱼群。在可行域S内随机生成N条人工鱼。第i条人工鱼的当前位置为Xi，其对应的食物浓度Yi(=-f(Xi))(i=1,2,…,N)。

步骤3测定N条人工鱼在当前位置下的食物浓度Yi(1≤i≤N),记录食物浓度最大值Ymax和相应的位置Xmax，即作为公告板的初始记录(Xmax,Ymax)。

步骤5动态拥挤度因子δk：

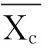
(1)

步骤8觅食。在人工鱼Xi的视野范围内随机选择一个位置Xj。若Yj>Yi，则朝Xj的方向按照式(1)中的方法前进一步，否则重新随机选择位置Xj，判断是否满足前进条件。若尝试Try_number次后仍不满足前进条件，则执行步骤9。

步骤9随机移动。人工鱼在其可行域S内按照式(2)随机移动一步，产生一个新的位置Xnext。

Xnext=Xi+Rand()×step

(2)

步骤11用新确定的人工鱼位置，从步骤4开始重新搜索，直到迭代结束。

2实验与仿真

2.1高维优化函数极值问题

选择以下非线性优化函数来验证自适应重生鱼群优化算法的性能：

(3)

该非线性优化函数的全局最优解的周围分布着很多局部最优解。且容易看出，对任意的自然数n，该优化问题的最优解为X=0，最优值为1。

下面的仿真实验中，算法参数设置如下：人工鱼的数量为50，视野范围为1，移动步长为0.05，最大试探次数为50，最大迭代次数的设定:实验1为500次，实验2和3为50次。

实验1图2为采用传统人工鱼群算法求解式(3)所得的最优值随维数n的变化曲线；图3为维数n=11时传统人工鱼群算法的寻优曲线。从图2可以看出随着维数n的增大，传统人工鱼群算法的最优值越来越偏离1，精度大大地降低。当维数n>5时，传统人工鱼群算法的求解误差≥0.25，所以其适用范围受到一定的局限性。且从图3中可以看出当维数n=11时，传统人工鱼群算法在迭代初期就陷入局部最优，始终无法跳出，所得的最优值0.366与1相差很大。

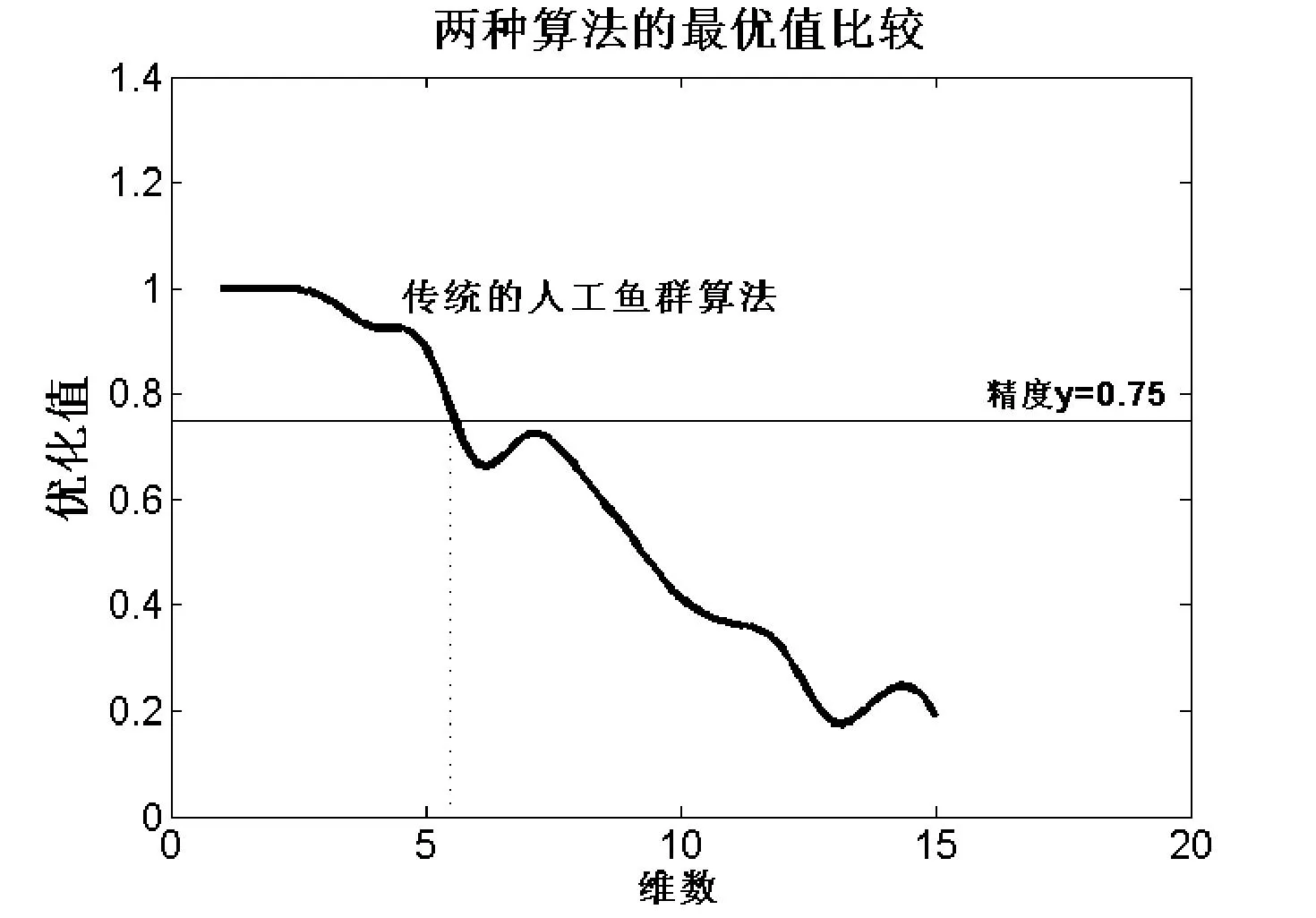
图2　传统人工鱼群算法随优化函数维数的变化曲线

图3　维数n=11

通过实验1可以得出：如果问题(3)要求求解误差≤0.25，则传统人工鱼群算法的适用范围为维数n≤5。但是实际的工程问题很复杂，所对应的优化问题的维数往往不止5。

实验2图4-图6为自适应重生鱼群优化算法与传统的人工鱼群算法维数不同比较的仿真结果。图4表示当维数为2时,两种算法寻优曲线的比较。从图4可以看出虽然两种算法都能得到最优值，但改进后的人工鱼群算法比传统的人工鱼群算法的收敛速度快。图5表示当维数为5时，两种算法寻优曲线的比较。从图5可以看出当迭代次数为40次时，传统的人工鱼群算法已经陷入局部最优，并且所得的最优值0.87。但是自适应重生鱼群算法所得的最优值仍能逼近于1，求解精度比传统的人工鱼群算法高，且收敛速度快。图6表示当维数为11时，两种算法寻优曲线的比较。从图6可以看出传统的人工鱼群算法所求的最优值在0.4左右，与式(3)的最优值偏离很大，已经无法适用。但是自适应重生鱼群算法所得最优值仍保持在0.75以上，求解精度仍比传统的人工鱼群算法高。

图4　维数n=2

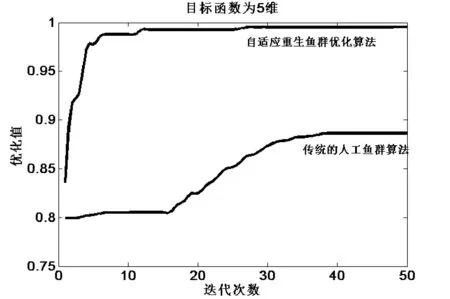
图5　维数n=5

图6　维数n=11

通过实验2可以得出：本文自适应重生鱼群优化算法在收敛速度和全局寻优能力上都比传统的人工鱼群算法更佳，大大拓宽了人工鱼群算法的适用范围，在解决复杂的工程问题上更胜一筹。

实验3图7为两种算法运行时间的比较结果。从图7可以看出在相同的迭代次数内，当维数n≥6时，两种算法的运行时间相当，也就是说，与传统人工鱼群算法相比，本文算法的复杂度并没有增加，说明本文提出的算法不仅复杂度没有增加，且各项性能都有大幅度的提高，在工程上适用范围广。

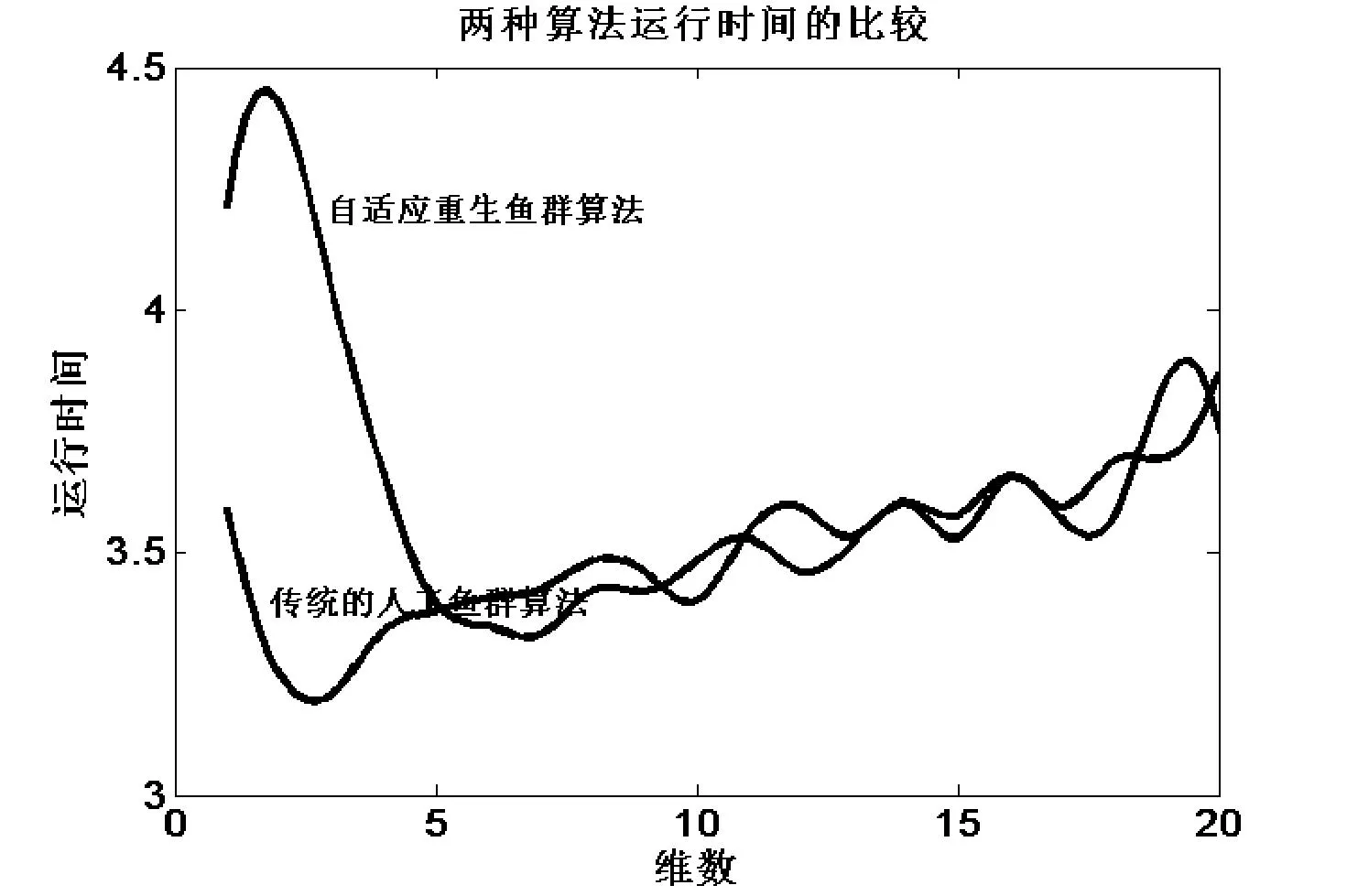
图7　两种算法运行时间的比较

由此可以得出结论：处理高维优化函数问题时，自适应重生鱼群优化算法与传统人工鱼群算法相比，具有寻优速度快、精度高、复杂度相当等优点，成功地拓宽了其在工程上的应用。

2.2旅行线路的优化

旅游线路的优化的问题是旅行商(TSP)问题的一种典型代表。近几年来对于TSP问题的求解提出了许多优化算法，其中仿生算法是研究的热点[9-12]。它具有传统算法不可替代的优势,如：非线性性、自组织性和并行性等。本文引用文献[13]中设计旅行线路为例，来直观地反映自适应重生鱼群优化算法与其他算法的优劣。

按照实数编码的原理，对各个城市进行重新编号。为验证本文算法的性能，同时引入遗传算法和传统的人工鱼群算法进行求解。此时的优化函数为城市之间的欧氏距离之和。相关参数设置如下：人工鱼数目为10;最大迭代次数：遗传算法为1500，传统和改进后的人工鱼群算法为500;最多试探次数为100；视野范围为6;移动步长为2；拥挤度因子为0.8(遗传算法与文献[13]的参数设置一致)。现设置出发点都为重庆，且必须经过每一个城市且仅一次，最后回到重庆。

由文献[13]可知，利用遗传算法得出的最优路线，所对应的最优值为18 997.8km。采用传统的人工鱼群算法设计旅行路径的结果，其对应的最优值为18 596.9km。从优化效果来看，传统人工鱼群算法的寻优效果比遗传算法的效果更好些。采用自适应重生鱼群优化算法设计旅行路径的结果。对应的线路安排如下：重庆—>贵州—>南宁—>海口—>澳门—>香港—>广州—>长沙—>合肥—>南京—>上海—>杭州—>台北—>福州—>南昌—>武汉—>郑州—>太原—>石家庄—>济南—>哈尔滨—>长春—>沈阳—>天津—>北京—>呼和浩特—>西安—>银川—>兰州—>西宁—>乌鲁木齐—>拉萨—>昆明—>成都—>重庆；所对应的最优值为17 595.3km。从优化效果来看，自适应重生鱼群优化算法的寻优效果比遗传算法和传统的人工鱼群算法的效果都更佳。图8为自适应重生鱼群算法的寻优效果图。从寻优的速度来看，本文算法能够快速地找到较优路径，并且运行时间短。

图8　自适应重生鱼群优化算法的寻优效果图

通过三种算法的比较可以得出：本文在迭代过程中采用鱼群重生和利用正态分布调整拥挤度因子的思想设计所得的自适应重生鱼群优化算法，在实际的应用中能够得到更佳的效果，并且求解精度高，收敛速度快，成功地拓宽了传统的人工鱼群算法在工程上的应用。

3结语

本文针对人工鱼群算法在处理高维优化函数时的缺点，提出了自适应重生鱼群算法。通过鱼群重生和利用正态分布动态调整拥挤度因子的结合，不仅每次迭代都给鱼群注入“新生命”，使鱼群得以重生，而且能自适应地调整鱼群的行为。实验表明：经自适应重生鱼群优化算法提高了求解高维优化函数的收敛速度和精度。最后为验证本文算法的有效性，将其用于34个城市旅游线路的优化，并与传统的人工鱼群算法和遗传算法相比。结果表明：本文算法寻优精度高，得到的线路最优，成功地拓宽了其在工程上的应用。

参考文献

[1] 李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式：鱼群算法[J].系统工程理论与实践,2002,22(11):32-38.

[2] 李晓磊,钱积新.基于分解协调的人工鱼群优化算法研究[J].电路与系统学报,2003,8(1):1-6.

[3] 李晓磊,路飞,田国会,等.组合优化问题的人工鱼群算法应用[J].山东大学学报:工学版,2004,34(5):64-67.

[4] 李亮,迟世春,林皋.禁忌鱼群算法及其在边坡稳定分析中的应用[J].工程力学,2006,23(3):6-10.

[5] 方金城,张岐山.配送中心配送决策问题及其鱼群算法优化求解[J].计算机应用,2011,31(6):1652-1655.

[6]ZhangK,ZhangW,DaiCYEal.Artificalfish-swarmbasedconverage-enhancingalgorithmforvisiblelightsensornetworks[J].Optoelectronicletters,2010,6(3):229-231.

[7] 陈安华,周博,张会福,等.基于改进人工鱼群算法的机械故障聚类诊断方法[J].振动与冲击,2012,31(17):145-148.

[8] 王晔,吴小俊,王士同.基于改进人工鱼群算法的RBF网络及其在人脸表情识别中的应用[J].计算机应用研究,2008,25(9):2643-2646.

[9]ZhangZhigang,LiXiaojing.BasedonTSPProblemtheResearchofImprovedAntColonyAlgorithms[J].ElectricalEngineeringandControl,2011,98(2):827-833.

[10] 郑立平,郝忠孝.基于混合杂交的遗传算法求解旅行商问题[J].计算机工程,2005,20(31):168-172.

[11] 黄岚,王康平,周春光,等.粒子群优化算法求解旅行商问题[J].吉林大学学报:理学版,2003,4(41):477-480.

[12] 杨剑峰,蒋静坪.蚁群算法及其在组合优化问题中的应用[J].科技通报,2006,4(22):553-556.

[13] 走遍全中国方案的研究[EB/OL].(2014.05.30.)http://www.docin.com/p-105402921.html.

[14]TizhooshH.opppsition_basedlearning:Anewschemeformachineintelligence[C]//ProceedingsoftheInternationalConferenceonComputationalIntelligenceforModelingControlandAutomation,2005:695-701.

[15]WangHui,LiuY,ZengSY,etal.Opposition-basedParticleSwarmAlgorithmwithCauchyMutation[C]//Proc.Congr.Evol.Comput,2007:4750-4756.

ADAPTIVE REBORN FISH SCHOOL OPTIMISATION ALGORITHM

Yi Zhengjun1Wei Leipeng1Yuan Yuxing2

1(College of Mathematics and Statistics,Chongqing University,Chongqing 401331,China)2(School of Mathematics and Science,Chongqing University of Science and Technology,Chongqing 401331,China)

AbstractTraditional artificial fish school algorithm converges slowly and is prone to falling into local optimum when solving high-dimensional optimisation problems. In light of this, we presented the adaptive reborn fish school optimisation algorithm. First, in the process of each iteration we injected the "new life" into fish school incessantly, which made the rebirth of the fish school; Then we used normal distribution to dynamically adjust the upper threshold of crowding factor, making the algorithm more close to the process of fish school’s forage. Experimental result showed that the improved algorithm ensured the convergence speed and increased the probability of the algorithm in obtaining global optimum, yet it were also suitable for solving large-scale optimisation problems. Two examples in the paper were optimised by the improved fish school algorithm, the optimisation results were in good conformity with the reality, this illustrated the effectiveness and practicability of the improved algorithm.

KeywordsArtificial fish school algorithmFish rebirthNormal distributionDynamic crowding factorOptimisation

收稿日期：2014-11-27。国家自然科学基金项目(11371384，6967 4012)；重庆市科技攻关计划项目(CSTC2009AC3037)。易正俊，教授，主研领域：人工智能，智能算法，信息融合与处理。韦磊鹏，硕士生。袁玉兴，助教。

中图分类号TP3

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.055