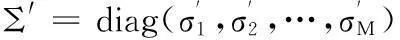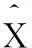基于奇异值分解的Toeplitz结构测量矩阵构造方法

赵　辉　金胜杰

(重庆邮电大学光通信与网络重点实验室　重庆 400065)



基于奇异值分解的Toeplitz结构测量矩阵构造方法

赵辉金胜杰

(重庆邮电大学光通信与网络重点实验室重庆 400065)

摘要在压缩感知CS(Compressed Sensing)理论中，测量矩阵的构造至关重要，其性能直接影响到数据压缩采样的效率及信号的重构质量。针对Toeplitz结构测量矩阵重构性能不高的问题，提出一种基于奇异值分解的Toeplitz结构测量矩阵构造方法。首先对Toeplitz矩阵进行奇异值分解，然后通过对该矩阵的非零奇异值进行优化来提高矩阵的列向量独立性，从而提高其重构性能。仿真结果表明，相比较未优化的Toeplitz结构测量矩阵以及当前常用的高斯随机矩阵，当采用优化后的Toeplitz结构测量矩阵对信号进行压缩感知时，信号的重构精度得到显著提高。

关键词压缩感知测量矩阵托普利兹结构奇异值分解信号重构

0引言

压缩感知CS[1,2]理论突破了奈奎斯特采样定理对信号采集与处理的限制，实现了数据采集与数据压缩的同时进行。在很大程度上减少了数据采样所需要的时间和存储数据所需要的空间，为图像信号的采集和压缩的研究提供了一种新的理论依据。在压缩感知理论中，测量矩阵性能的优劣直接关系到信号重建精度的高低与重构速度的快慢。当前常用的测量矩阵大部分是随机的，然而，这类矩阵通常不易于硬件实现，由于将测量矩阵予以硬件实现是压缩感知理论应用到实际中的一个重要条件。因此，构造具有较高重构性能并且易于硬件实现的的测量矩阵具有重要意义。

根据矩阵元素的随机性和确定性可将测量矩阵分为两类，即随机测量矩阵和确定性测量矩阵[3]。随机测量矩阵包含高斯随机矩阵、稀疏投影矩阵以及贝努利矩阵等。其主要特点是矩阵的每个元素都服从独立同分布，因此随机测量矩阵的列向量具有较好的非相关性，所以只需较少的采样值就能完成原信号的精确重建。但是，随机测量矩阵占用存储空间较大、计算复杂度高且难以硬件实现。确定性矩阵包括Toeplitz结构测量矩阵、循环矩阵等，其主要特点是易于硬件实现，但相比较随机测量矩阵，其重构性能较低。在确定性测量矩阵中[4-7]，Toeplitz结构测量矩阵是通过行向量的循环移位来构造整个矩阵。在实际应用过程中，这种循环移位非常易于硬件实现，并且Toeplitz矩阵是一种高度结构化的矩阵，矩阵的结构化可以提升计算速度及降低计算复杂度。然而同大多数确定性测量矩阵[8,9]一样，Toeplitz矩阵相比较高斯随机矩阵等随机测量矩阵也存在重建精度不高的问题[10-12]。为了确保原信号进行较高精度的重建，通常需要较多数目的测量值，而在实际应用中获得较多测量值需要付出很大的代价。

针对易于硬件实现的Toeplitz矩阵重构性能较低的问题，本文提出一种基于奇异值分解的Toeplitz结构测量矩阵构造方法。通过对该矩阵的奇异值进行优化来提高测量矩阵的列向量独立性，从而提高其重构性能。仿真结果表明：在相同的稀疏基和重构算法下，无论是重构图像的视觉效果还是重构图像的客观评价指标数值，当采用本文方法优化后的Toeplitz结构测量矩阵进行压缩感知时，总体上图像信号重构结果要好于采用未优化的Toeplitz测量矩阵和高斯随机矩阵时的情况，即本文构造的基于奇异值分解的Toeplitz结构测量矩阵具有较好的重构性能。

1压缩感知理论框架

1.1压缩感知理论的数学模型

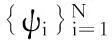
(1)

其中，式(1)中Ψ=[ψ1,ψ2,…,ψN]为N×N的正交基矩阵，θ=[θ1,θ2,…,θN]T为系数向量。若系数向量θ中只有K(K≪N)个非零系数，那么称信号x在基矩阵Ψ下为K稀疏信号。将信号x投影到与稀疏基不相关的测量矩阵ΦM×N(M≪N)上，即对信号x执行压缩观测，可得：

y=Φx=ΦΨθ

(2)

信号的重建就是通过M维的测量值y来恢复N维的原始信号x，由于测量值维数M≪N，因此求解式(2)的过程是病态的，即无法直接求解。但是若原信号x是稀疏的或可压缩的，且测量矩阵满足有限等距性质RIP(RestrictedIsometryPrinciple)[1,2]，那么可通过求解下述最小l0范数问题来精确求解原始信号x，即：

(3)

由于对l0范数问题的求解是NP-hard的，且最小l0范数问题和最小l1范数问题在测量矩阵满足RIP的条件下是等价的[1]，因此式(3)可转化为：

(4)

压缩感知过程如图1所示。

图1压缩感知过程

1.2测量矩阵满足的约束条件

测量矩阵是压缩感知理论的重要组成部分，为了确保信号进行有效的压缩和精确的重构，测量矩阵应满足一定的条件。Candes等人提出了测量矩阵所满足的RIP准则[13]，该准则的数学描述为：对于任意K稀疏信号x和常数δK∈(0,1)，如果：

(5)

成立，则称测量矩阵满足有限等距性质。

在测量矩阵的构造过程中，几乎很难验证矩阵是否满足RIP条件。通常可以采用同RIP准则等价的性质，即矩阵非相干性[14,15]来作为测量矩阵构造的理论指导。研究表明：在正交稀疏基Ψ确定的情况下，可从测量矩阵的列向量相关性方面入手设计测量矩阵。为了指导构造测量矩阵，在文献[1]中Donoho给出了测量矩阵所要满足的三个基本特征：(1) 由测量矩阵的列向量组成的子矩阵的最小奇异值必须大于一定的常数，即测量矩阵的列向量在一定程度上要具有较好的线性非相干性；(2) 测量矩阵的列向量要满足一定程度上的随机性；(3) 在一定稀疏度条件下的解则为满足1-范数最小的列向量。这三个特征为测量矩阵的构造提供了重要指导，同时也是本文测量矩阵优化算法的重要理论依据。

2基于奇异值分解的Toeplitz结构测量矩阵构造方法

奇异值分解SVD(SingularValueDecomposition)广泛应用于信号与图像处理、最小二乘问题、酉不变范数理论、特征值问题以及优化问题等领域。它是矩阵论和线性代数中一种很重要的矩阵分解算法[16-21]。

2.1矩阵奇异值分解

(6)

其中，Σ=diag(δ1,δ2,…,δr)，U满足UHAAHU是对角矩阵，V满足VHAHAV是对角矩阵。那么称式(6)为矩阵A的奇异值分解。矩阵奇异值分解具有以下主要性质：

性质1矩阵非零奇异值的个数与该矩阵的秩相等。设矩阵A∈Cm×n，且其秩rank(A)=r，则A的奇异值满足σ1≥σ2≥…≥σr>σr+1=…=σm=0。

2.2基于奇异值分解的Toeplitz结构测量矩阵优化算法

测量矩阵要满足的第一个特征指出：测量矩阵的列向量要具有比较好的线性非相关性，然而矩阵的线性非相关性与矩阵的最小奇异值密切相关。若矩阵的最小奇异值越小，那么矩阵的线性相关性越大，即其独立性越弱。当测量矩阵最小的奇异值近似为0时，则矩阵列向量的线性独立性趋于最小。因此，本文提出了一种基于奇异值分解的Toeplitz结构测量矩阵设计方法，目的是通过增大矩阵的奇异值来提高矩阵列向量的线性独立性。

通常情况下，理论上常用的测量矩阵在实际应用中具有局限性，难以硬件实现，满足一定条件的测量矩阵才能更好地予以硬件实现。文献[3]给出了能在实际中应用的测量矩阵应满足以下性质：(1) 测量矩阵和稀疏基矩阵要具有较强的不相干性，以确保信号进行较高精度的重建；(2) 测量值的数目要尽量与理论值相接近，以降低获取测量值的成本；(3) 矩阵要具有较强的结构性，以减小采样与重建的复杂度；(4) 占用存储空间小，构造元素简单，并且易于硬件实现。因此，为了使构造的Toeplitz结构测量矩阵结构简单，并且能够更好地通过实际硬件予以实现，那么该矩阵的元素可由0、1来组成。

综上，该方法首先生成一个元素由0、1随机组成的行向量u=(u1,u2,…,uN,uN+1,…,uN+M-1)。然后根据向量u来构造Toeplitz结构测量矩阵Φ，接下来对测量矩阵Φ进行奇异值分解，并对奇异值进行优化处理，得到新的测量矩阵Φ′。并且该优化过程并没有改变矩阵非零奇异值的个数，因此，由性质1可知，该优化过程并没有改变矩阵的秩。然后再根据性质2和推论1，对新构造的测量矩阵Φ′作负元素置0，非负元素置1的近似处理，得到最终由0、1元素组成的Toeplitz结构测量矩阵Φ″。具体步骤如下：

步骤1生成一个随机向量u，其元素由满足随机分布的0、1组成，即u=(u1,u2,…,uN,uN+1,…,uN+M-1)；

步骤2利用步骤1生成的向量u构造Toeplitz结构测量矩阵Φ∈RM×N(M

(7)

步骤3对矩阵Φ∈RM×N(M

(8)

其中矩阵U、V分别为M×M维和N×N维的酉矩阵，Σ=diag(σ1,σ2,…,σM)，σ1≥σ2≥…≥σM为矩阵Φ的非零奇异值；

步骤5构造新的测量矩阵Φ′。

(9)

步骤6将矩阵Φ′的元素进行近似处理，即将测量矩阵Φ′中非负元素置1，负元素置0，得到最终所求测量矩阵Φ″。

对Toeplitz结构测量矩阵进行优化的流程如图2所示。

图2　优化算法流程图

3仿真结果与分析

为了验证本文提出的基于奇异值分解算法构造的Toeplitz结构测量矩阵的性能，采用两幅标准灰度测试图像Lena和Peppers进行仿真，且这两幅图像的分辨率均为256×256。各个测量矩阵在图像的压缩感知过程中采用相同的稀疏变换基和重构算法，即首先对这两幅图像采用小波变换进行稀疏表示。然后再分别利用高斯随机矩阵、元素由0、1组成的Toeplitz结构测量矩阵以及采用本文算法优化后的由0、1元素组成的Toeplitz结构测量矩阵对稀疏变换后的图像信号进行压缩投影。最后选用OMP重构算法来重构原始图像。

本文通过重构图像的峰值信噪比PSNR和图像匹配度match两项指标来对图像的重构质量进行衡量。峰值信噪比和匹配度的定义如下：

PSNR=10lg(2552/MSE)

(10)

同样地，重构图像匹配度match可表示为：

(11)

表1和表2分别表示当测量矩阵为未优化的Toeplitz测量矩阵、高斯随机矩阵以及本文算法优化后的Toeplitz测量矩阵时，重构图像的峰值信噪比及图像匹配度随采样率变化的仿真结果比较。

表1　测试图像仿真结果峰值信噪比值比较

表2　测试图像仿真结果匹配度值比较

由表1和表2可知，重构图像的峰值信噪比和图像匹配度均随着采样率的增大而增加。从表1可以明显看出，当信号采样率一定的情况下，采用优化后的Toeplitz结构矩阵作为测量矩阵时，重构图像的PSNR值要高于采用高斯随机矩阵和未优化的Toeplitz矩阵作为测量矩阵时的情况。同样地，从表2可以得到，当测量矩阵为优化后的Toeplitz矩阵时，在采样率相同的条件下，重构图像的匹配度要高于采用其他两种测量矩阵时的情况。表1和表2的仿真结果说明采用本文算法优化后的Toeplitz结构测量矩阵的重构性能得到显著提高。

为了直观验证优化后的Toeplitz结构测量矩阵的重构性能，图3与图4分别给出了不同采样率下Lena图像与Peppers图像采用高斯随机矩阵、Toeplitz结构测量矩阵及优化后的Toeplitz结构测量矩阵进行观测时的峰值信噪比对比图；同样地，图5与图6分别给出了不同采样率下这两幅图像采用高斯随机矩阵、Toeplitz结构测量矩阵及优化后的Toeplitz结构测量矩阵进行观测时的匹配度对比图。

图3　Lena图像在不同测量矩阵下的PSNR值比较

图4　Peppers图像在不同测量矩阵下的PSNR值比较

图5　Lena图像在不同测量矩阵下的match值比较

图6　Peppers图像在不同测量矩阵下的match值比较

从图3和图4可以看出，随着采样率的增大，图像的峰值信噪比逐渐增加，表明这几种测量矩阵的重构效果随着采样率的增大逐渐增强。此外，在相同的采样率下，当测量矩阵为高斯随机矩阵时，重构图像的PSNR值大于测量矩阵为未优化的Toeplitz矩阵时的情况。而本文对Toeplitz矩阵进行优化处理后，其重构图像的PSNR值又大于采用高斯随机矩阵时的情况。并且在采样率大于0.5时，重构图像PSNR值趋于近似线性增加。

同样由图5和图6可得，采用优化后的Toeplitz矩阵作为测量矩阵时，在同样的采样率下，重构图像的匹配度值大于采用高斯随机矩阵和未优化的Toeplitz矩阵时的情况，表明优化后的Toeplitz矩阵具有较高的重构精度。因此，本文对Toeplitz矩阵优化后，可显著提高重建图像的PSNR值及匹配度值。

为了进一步对比高斯随机矩阵、Toeplitz结构测量矩阵、优化后的Toeplitz结构测量矩阵的重构性能，图7和图8分别给出了Lena与Peppers图像在相同的稀疏基和重构算法下，当采样率为0.5时重构图像的视觉效果比较。

图7　Lena图像在采样率为0.5时的重构效果图

图8　Peppers图像在采样率为0.5时的重构效果图

从图7和图8可以看出，当采样率取值0.5时，测量矩阵为高斯随机矩阵时重构图像的视觉效果要优于测量矩阵为未优化的Toeplitz矩阵的情况。并且当测量矩阵为优化后的Toeplitz结构测量矩阵时，重构图像的视觉效果又好于采用高斯随机矩阵的情况。尤其是采用优化后的Toeplitz结构测量矩阵对图像进行压缩观测时，重构图像的边缘及轮廓更加清晰，块效应较弱，即显著提高了图像重建质量。

4结语

针对易于硬件实现的Toeplitz结构测量矩阵重建精度不高的问题，本文提出了一种基于奇异值分解的Toeplitz结构测量矩阵优化方法。将Toeplitz结构测量矩阵进行奇异值分解，并对该矩阵的奇异值进行优化处理，通过增大矩阵的奇异值来提其列向量线性独立性，进而提高其重构性能。仿真结果表明：相比较当前常用的高斯随机矩阵以及未优化的Toeplitz结构测量矩阵，采用本文提出的基于奇异值分解的Toeplitz结构测量矩阵作为测量矩阵进行图像信号压缩感知时，重构图像的匹配度、PSNR值均得到了显著提高，并且重构图像的主观视觉效果也得到了明显提升。因此，本文提出的Toeplitz结构测量矩阵优化方法有效提高了该测量矩阵的重构性能。

参考文献

[1]DonohoDL.Compressedsensing[J].IEEETransactionsonInformationTheory,2006,52(4):1289-1306.

[2] 焦李成,杨淑媛,刘芳,等.压缩感知回顾与展望[J].电子学报,2011,39(7):1651-1662.

[3] 秦周.压缩感知中测量矩阵的优化与构造方法[D].北京:北京交通大学,2012.

[4]MonajemiH,JafarpourS,GavishM,etal.DeterministicmatricesmatchingtheCompressedSensingphasetransitionsofGaussianrandommatrices[J].ProceedingsoftheNationalAcademyofSciences,2013,110(4):1181-1186.

[5]TehraniAS,DimakisAG,AireG.OptimaldeterministicCompressedSensingmatrices[C]//IEEEInternationalConferenceonAcoustics,SpeechandSignalProcessing(ICASSP).Vancouver:IEEEPress,2013:5895-5899.

[6]LiS,GeG.Deterministicsensingmatricesarisingfromnearorthogonalsystems[J].IEEETransactionsonInformationTheory,2014,60(4):2291-2302.

[7] 王强,李佳,沈毅.压缩感知中确定性测量矩阵构造算法综述[J].电子学报,2013,41(10):2041-2050.

[8]BlanchardJD.TowarddeterministicCompressedSensing[J].ProceedingsoftheNationalAcademyofSciences,2013,110(4):1146-1147.

[9]LiKezhi,LuGan,CongLing.ConvolutionalCompressedSensingusingdeterministicsequences[J].IEEETransactionsonSignalProcessing,2013,61(3):740-752.

[10]HauptJ,BajwaWU,RazGM,etal.ToeplitzCompressedSensingmatriceswithapplicationstosparsechannelestimation[J].IEEETransactionsonInformationTheory,2010,56(11):5862-5875.

[11]SebertF,ZouYiming,YingLeslie.ToeplitzblockmatricesinCompressedSensingandtheirapplicationsinimaging[C]//IEEE.InformationTechnologyandApplicationsinBiomedicine(ITAB).Shenzhen:IEEEpress2008:47-50.

[12]BajwaWU,HauptJD,RazGM,etal.Toeplitz-structuredCompressedSensingmatrices[C]//IEEE.StatisticalSignalProcessing(SSP).Madison,USA:IEEEPress,2007:294-298.

[13]CandèsEJ,RombergJ,TaoT.Robustuncertaintyprinciples:Exactsignalreconstructionfromhighlyincompletefrequencyinformation[J].IEEETransactionsonInformationTheory,2006,52(2):489-509.

[14]BlumensathT.CompressedSensingwithnonlinearobservationsandrelatednonlinearoptimizationproblems[J].IEEETransactionsonInformationTheory,2013,59(6):3466-3474.

[15]EladM.OptimizedprojectionsforCompressedSensing[J].IEEETransactionsonSignalProcessing,2007,55(12):5695-5702.

[16]LaiCC,TsaiCC.Digitalimagewatermarkingusingdiscretewavelettransformandsingularvaluedecomposition[J].IEEETransactionsonInstrumentationandMeasurement,2010,59(11):3060-3063.

[17]KleibergenF,PaapR.Generalizedreducedranktestsusingthesingularvaluedecomposition[J].Journalofeconometrics,2006,133(1):97-126.

[18]CajJianfeng,CandèsEJ,ShenZuowei.Asingularvaluethresholdingalgorithmformatrixcompletion[J].SIAMJournalonOptimization,2010,20(4):1956-1982.

[19]CongedoM,PhlypoR,PhamDT.Approximatejointsingularvaluedecompositionofanasymmetricrectangularmatrixset[J].IEEETransactionsonSignalProcessing,2011,59(1):415-424.

[20]SatoH,IwaiT.ARiemannianoptimizationapproachtothematrixsingularvaluedecomposition[J].SIAMJournalonOptimization,2013,23(1):188-212.

[21]SavasB,EldénL.Handwrittendigitclassificationusinghigherordersingularvaluedecomposition[J].Patternrecognition,2007,40(3):993-1003.

TOEPLITZ STRUCTURE MEASUREMENT MATRIX CONSTRUCTION METHOD BASEDONSINGULARVALUEDECOMPOSITION

Zhao HuiJin Shengjie

(Key Laboratory of Optical Communication and Networks,Chongqing University of Posts and Telecommunictions,Chongqing 400065,China)

AbstractThe construction of measurement matrix is crucial to compressed sensing theory, its performance directly affects the efficiency of data sampling compression and the quality of signal reconstruction. In view of the fact that the performance of Toeplitz structure measurement matrix reconstruction is not high, we proposed a singular value decomposition-based construction method for Toeplitz structure measurement matrix. First, it decomposes the Toeplitz matrix by using singular value decomposition algorithm, then it enhances the independence of column vectors of the matrix by optimising its nonzero singular values, so as to improve the reconstruction performance. Simulation results showed that compared with the non-optimised Toeplitz structure measurement matrix and the frequently used Gauss random matrix, the signal reconstruction accuracy gained significant improvement when using the optimized Toeplitz structure measurement matrix to carry out compressed sensing on signals.

KeywordsCompressed sensingMeasurement matrixToeplitz structureSingular value decompositionSignal reconstruction

收稿日期：2014-12-10。国家自然科学基金项目(61271261)；重庆市科委自然科学基金项目(CSTC2012jjA40048)。赵辉，副教授，主研领域：现代信号与图像处理，空间光通信及光信息处理。金胜杰，硕士生。

中图分类号TP301

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.044