科学确证的贝叶斯网络模型

张　顺

(南京大学 哲学系，南京　210023)



科学确证的贝叶斯网络模型

张顺

(南京大学 哲学系，南京210023)

摘要：科学确证的假说演绎模型与贝叶斯确证模型分别体现了定性确证与定量确证的内涵，然而科学确证是一个在纵横方向都具备复杂内涵的问题，两种模型均没克服因确证本身的复杂性与非单调性所带来的一些难题。为此，将贝叶斯网络方法运用到确证理论的建构中，通过图论与贝叶斯确证理论的结合开拓确证理论研究的新进路，并构建贝叶斯确证网络的简单模型。同时，从模型的定义、结构建模、推理等方面阐述贝叶斯确证网络的基本内容。

关键词：科学确证；贝叶斯确证；贝叶斯确证网络

一、前言

观察证据E确证假说H，当且仅当，(1) E为偶然真；(2) H├E。

这些重构方案各自存在着不同程度的缺陷，这些缺陷在H-D的现有框架内是无法克服的，因为这个简洁模型无法完全表现确证的本质。这一模型基本成功地刻画了确证的第一层含义，它表明证据为理论提供了某种确定性的支持，这是确证的定性层面。然而，就科学检验的定性层面而言，不存在完全证实，只有弱证实性确证。我们可以做的只能是越来越逼近那不可能达到的证实，不断提高理论的确证程度。这就涉及到科学检验的定量层面，需要引进逻辑概率进行定量刻画。

贝叶斯确证理论的要义在于用概率来定量地测度证据对假说的支持程度。凯恩斯认为概率关系应当表示为P(a/h)，即a与h之间的相对概率，对于不同的前提h，a/h的值可能不同。对于互为前提的两个命题集，它们的条件概率将满足一定的运算定理。18世纪的英国数学家托马斯·贝叶斯提出了计算条件概率的公式：

(1)

用以描述两个条件概率的关系，由此可以从旧的概率条件性考查新信息的概率条件性，从而提供了一种知识更新或信念修正的方法。这样一来，条件概率正好可以说明确证中假说与证据的二元关系，假说或证据的命题本身的真假不是确证的主要内容，确证只能以条件概率的形式对假说与证据的相对关系进行量化描述，从而表达证据对假说的支持，而贝叶斯定理恰好提供了用条件概率刻画确证度的方法。

在运用贝叶斯方法来构造科学确证模型时，由于对概率解释的不同，分为逻辑贝叶斯派和主观贝叶斯派。同样是运用贝叶斯定理，逻辑主义者强调了其中精确而优雅的形式性与定量分析功能，主观主义者则关注整个公式体现出来的动态感与人文性。以主观贝叶斯确证模型为例，要建立科学确证的贝叶斯确证模型，就要将概率的公理化系统改造为命题的概率逻辑系统Pr，在这个系统中的贝叶斯定理可以表达为：

(2)

其中，Pr(e)﹥0，Pr(hi) ﹥0且h1，h2，…，hn是互斥且穷举的。

如果将这里的h1，h2，…，hn看作n个竞争假说，e代表经验证据，那么Pr(h)就表示假说的验前概率，用以表达认知主体对假说相对于背景知识所具备的合理信念度；条件概率Pr(e/h)表示的是假说h相对于证据e的似然度；而Pr(h/e)就表示h相对于e的条件概率，在这里就表示假说的验后概率，即给定事实e后假说h的概率，也就是我们关注的证据e对于假说h的确证度。在上述解释下，我们就可以把贝叶斯定理应用于科学假说的检验。在这里面，贝叶斯定理充当了从先验概率向后验概率过渡的桥梁，这其实就把证据与假说更直接地联系了起来，体现了证据对假说确证的动态过程[6]。

在人工智能领域，人们很早就注意到不确定性推理与归纳逻辑的关系，在20世纪60年代初将贝叶斯定理引入人工智能研究，这些可谓是早期的贝叶斯系统，这一系统的思路与卡尔纳普对概率的逻辑解释和他的可能世界语义类似。一方面，系统获取巨大的概率数据表，进行存储运算；另一方面，用原子事件和全联合分布的概率来描述世界，用若干原子事件的析取来表示各种命题或事件，而有了全联合分布概率表，就可以通过对命题中的原子事件的概率求和得到命题的概率。然而，正如卡尔纳普所遇到的困难一样，这种全联合分布面临着计算复杂的困难。对于二值随机变量，假设逻辑域中有n个随机变量，那么概率表中的原子事件为2n个，更别说要对这些原子事件进行联合运算，要计算的数目将达到一种惊人的程度，类似于“指数爆炸”。

有没有一种方法或者说找到某种独立性原则来将全联合分布分解为较小的联合分布呢？1986年，Pearl提出了作为专家系统的贝叶斯网络[7]，这一网络将概率论中的贝叶斯定理与运筹学中的图论相结合，通过概率模型中的条件独立性原则和图论中的d-separation标准将概率联合分布处理成更加简洁的形式。模型表达的复杂度得以降低，人们可以提高推理效率，用概率方法来解决大型问题。科学确证的问题同样是不确定性知识推理和复杂度较高的问题，可以尝试用贝叶斯网络来构建确证理论的新模型。

二、贝叶斯网络与贝叶斯确证

简单来说，贝叶斯网络就是一个具有因果语义的有向无环图(Directed acyclic graph，简称DAG)，它是贝叶斯方法与图论的有机结合。

(一)从图论到贝叶斯网络

图论是广泛应用于物理学、化学、控制论、计算机等多个领域的运筹学分支，一般一个图由一些点及点之间的连线组成。其中带箭头的连线称作弧，不带箭头的线称作边，根据图中的连线性质不同，可以分为有向图和无向图。贝叶斯网络的基本结构就是一个有向无环图(DAG)。在一个DAG中，结点通过有向弧建立起关联关系，被一条弧连接起来的结点称为邻居结点，若是由x指向y，则称x为y的父结点，y为x的子结点。有些结点没有父结点，则被称为根结点；有些结点没有子结点，则被称为叶结点。一个结点的父结点及父结点的祖先结点构成它的祖先结点；一个结点的子结点及子结点的后代结点构成它的后代结点。另一方面，这里的“无环”意味着图中不包含任何回路，也就是从x无法通过其他结点及有向弧的连接回到x。

在一个图模型中，可以用结点来表示问题域中的变量，用连线来表示变量之间的关系。这样图论也就为表达相互影响变量间的关系提供了直观的描述方法，符合人的自然理解和语义关系。同时，图论还可以运用知识表示不确定性建模及处理的方法，来直观描述变量间影响的定量化程度，从而通过参数模块的设置将整个复杂系统整体作为一个模块来研究。这是解决不确定性问题和复杂性问题的一种自然直观的方法[8]。

进一步讲，在有向无环图中，我们用结点来对应问题域中的属性描述，用有向边来表示属性之间的相互依赖关系，子结点的取值依赖于其父结点的值。如果我们将这种依赖关系在语义上解释为因果关系，或者说“当我们将因果解释赋予DAG中的有向边集合时，这个DAG图就变成一个因果网络”[9]。在因果解释下，每一个从父结点x到子结点y的过程都被解释为y因果依赖于x，而这时候就会引入概率来对这种因果支持语义进行具体的量化描述。因果网络使用的概率一般是主观概率，反映个体的知识状态和主观信念，能够很好地说明条件概率和条件独立。

(二)条件独立原则与d-separation标准

那么一个概率表示的因果网络又如何成为贝叶斯网络呢？

贝叶斯网络不仅是带有概率信息的有向无环图，而且在概率和图形方面都有相应的独立性规范。在这里，要同时运用概率论中的条件独立性与图论中的d-separation两条原则来对带有概率信息的因果网络进行规范。条件独立性也称之为马尔可夫条件，针对的是问题域中的变量，它要求在给定父结点变量的条件下，每个变量都独立于它的非后代结点。d-separation标准是定义有向无环图中结点关系的一条原则，简单说来就是结点集A的父结点集Pa(A) d-separation A和A的其他祖先结点集B。在直观的有向无环图中，d-separation就表现为Pa(A)“阻断”了所有从B到A的通路。

马尔可夫条件说明的是概率分布中变量间的条件独立关系，而d-separation则说明的是有向无环图中结点间的“幕隔”性。在一个概率因果网络中，d-separation恰恰是对结点所对应的变量间的条件独立关系的直观表达，我们很容易通过对结点在有向弧连接下的关系就判断它们所表示的变量是条件依赖关系还是条件独立关系。当然，在一个完整的因果网络中，还可能包含边缘独立等关系。如果用这两条标准来说明贝叶斯网络的定义，就可以作如下表述：如果有向无环图G是概率分布P的“独立性地图”，即G中的所有结点的d-separation性都对应着相应变量的概率条件独立性；并且G是P的最小“独立性地图”，即删除任何一条弧G都不再是P的“独立性地图”，那么就称G是P的贝叶斯网络[10]。

从确证理论模型的发展脉络来看，我们将贝叶斯确证模型当作是当前确证理论的代表模型，是对确证过程逻辑与非逻辑因素刻画的经典模型。贝叶斯网络模型是一个包括定性知识(结构关系、因果关系)和定量知识(概率、条件概率)的系统模型；它的推理原理基本是依据贝叶斯概率理论，贝叶斯方法是其计算的核心方法；它在结构上、数据上都能够表达因果性或概率支持语义。因此，理论上可以将贝叶斯确证与贝叶斯网络结合，构建出新的科学确证模型，以完整贴切地刻画科学理论的确证过程。如此构造的确证模型，本文称之为贝叶斯确证网络模型。

从贝叶斯确证的角度看，该模型的主要任务是将确证理论的传统表述用有向无环图重新构建出来，在贝叶斯网络中用结点间的关联来表达确证理论中假说与证据的关系，用条件概率分布表给出初始主观概率及相应的条件概率；从贝叶斯网络的角度看，就是将有向无环图的因果解释改变为科学确证解释，表明网络结构所表达的不是变量间的因果关系，而是假说与证据间的解释、支持或确证关系。

这样的网络是图论与确证理论的结合，由网络结构与网络参数两部分组成。有向无环图的结构表征确证域中相关假说与证据之间的关联信息，体现它们之间的条件依赖关系或独立关系；相关结点的参数设置则表征该变量的先验概率或者变量之间的条件概率，体现变量之间的相互影响程度。

三、结构与推理

贝叶斯网络是定性与定量方法的有机结合，其网络结构表达了定性知识，即变量间的因果联系；网络参数则表达了定量知识，即变量间影响的程度。整个网络构成了一种可视化、技术化的知识表达与推理模型，十分贴切地表示了结点间的因果关系。要建构贝叶斯确证网络，我们必须先对应贝叶斯网络的结构与推理机制。

(一)贝叶斯网络的结构与推理

我们可以将贝叶斯网络分为两部分来研究：网络结构与网络参数。其中，网络结构就是指有向无环图(DAG)，在贝叶斯网络中，结点同样表示随机变量，结点间的有向弧则表示了变量间可能的因果关系。结点与有向弧共同构成了贝叶斯网络的定性知识部分。在这样的结构中，结点与有向弧的图形化描述方法不仅直观体现了变量间的依赖关系，形成一个整体的可视的联合分布；同时也直接鲜明地表达了条件独立性的语义，可以看作是变量间条件独立性的一个自然的可视的“声明”。

对于变量间概率依赖强度的条件概率值的刻画是贝叶斯网络的参数部分，即条件概率分布表(Conditional probability distribution,简称CPD)。在贝叶斯网络中，每一结点都有一个该结点的边缘概率表(根结点对应的是边缘概率)或在给定父结点状态时的条件概率分布表。这些对于条件概率的具体刻画就形成了贝叶斯网络的定量知识层面。如此一来，就达到了对变量间依赖的程度的具体刻画，同时将复杂的知识系统分解成了若干较简易的概率表，从而降低了整个系统的复杂度。基于网络结构所声明的条件依赖性和独立性信息，就可以运用链式规则从条件概率表的参数得到整个网络的全联合分布。

图1就是一个简单的贝叶斯网络的例子，这其中有C(cloudy)、R(rain)、S(sprinkle)、W(wet pavement)四个变量或结点，结点间的影响关系通过有向线段表示出来；而每个结点旁边都有一个对应的概率分布表，分别说明每个结点在给定其父结点不同状态下成立或不成立的条件概率。其中Cloudy是没有父结点的根结点，故它的概率表是边缘概率表。

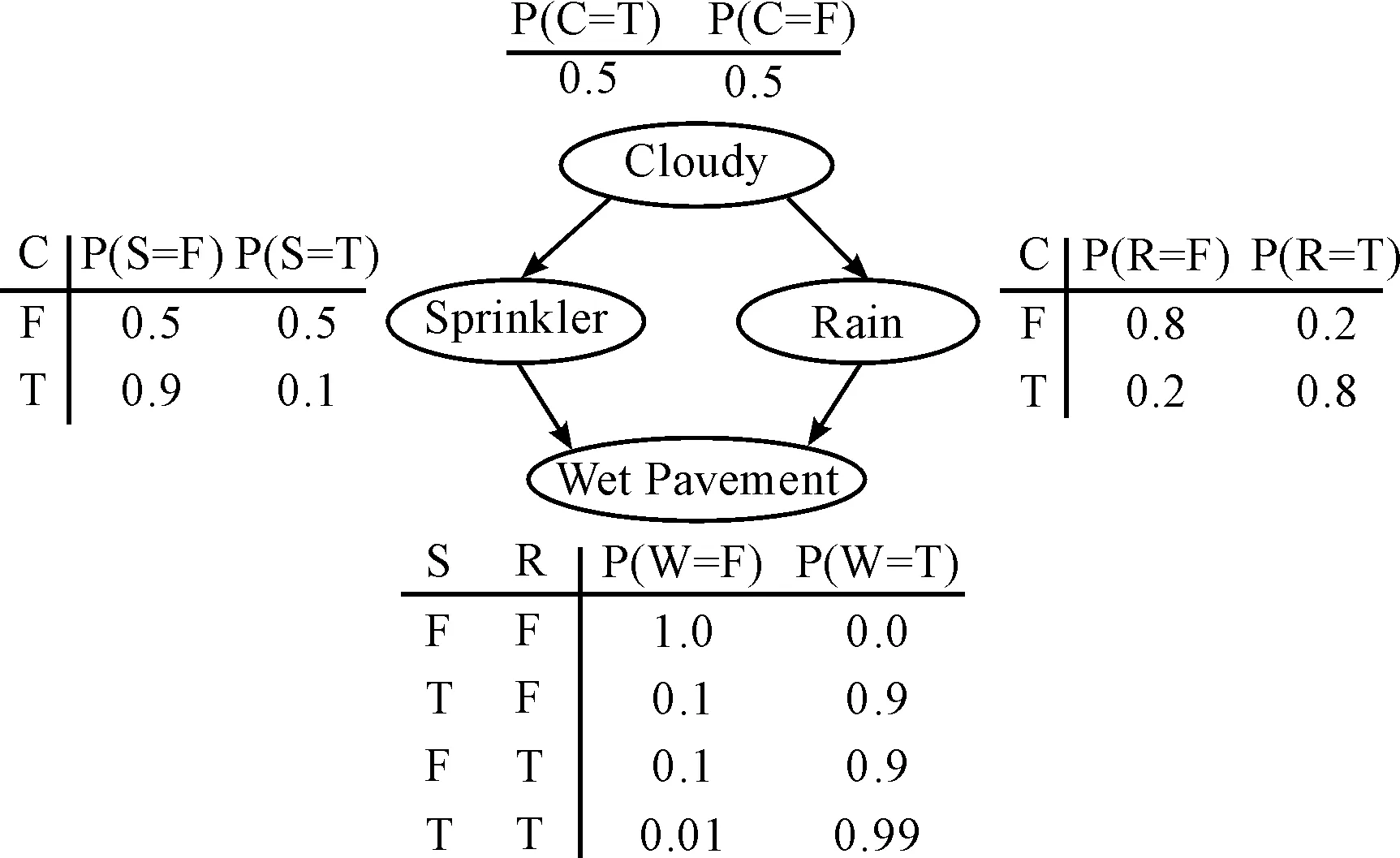
图1　一个贝叶斯网络的例子

在上述结构与参数描述下，变量间因果关系的条件依赖性与独立性都用图形的形式直观体现了出来，并且用概率分布表达了这种关系的具体程度，所以运用链式规则与贝叶斯定理的不确定性推理就可以进行。贝叶斯网络中的推理主要分为两种：因果推理与诊断推理。

因果推理即是网络中自上而下的推理，又称正向推理。它可以从有向弧的父结点信息运用因果推理算法得到子结点的相关状态信息，在风险系统中也可以根据初始信息来预测其它信息。在图1中，如P(W/S)的计算：

诊断推理是自下而上的推理，又称反向推理。这种推理可以用来根据观察到的结果查找相关的原因，诊断系统问题。在图1中，对P(S/W)的计算就是一种诊断推理：P(S/W)=P(W/S)P(S)/P(W)。

对于一个特定问题域而言，只要能明确理清该问题的语义系统，就可以运用专家知识根据因果关系进行结构建模(包括结点与变量的定义、结构的定义、结点状态的定义等)、参数建模(即是对整个网络的赋值)，表达出问题知识的基本形式和完整分布。而后再利用贝叶斯方法进行网络推理，根据研究目标得到需要的结果。

(二)贝叶斯确认网络的结构与推理

对贝叶斯确证网络模型的构建过程就是对贝叶斯网络模型进行重新建模的过程。对于科学确证问题而言，最重要的就是这一模型所呈现的结构、参数、推理是否表达了对应的语义，并且有助于相关问题的解决。相对来说，确证理论的贝叶斯网络模型是一个比较简单的贝叶斯网络，只涉及假说和证据两类变量。假说之间是相互竞争而独立的，证据之间也不会构成关联，而且它们之间的关系基本只有从假说到证据这一级。因此，贝叶斯确证网络模型的结构一般是拓扑结构，结点之间一般只有如图2所示的3种基本连接模式：顺连、分连、汇连。

图2　贝叶斯确证网络结点之间的关系

顺连表示假说H对证据E的直接影响，分连则表示同一假说既能解释证据E1又能解释证据E2，汇连则表示假说H1与H2共同影响E，或者说同一证据E既能说明假说H1又能说明假说H2。对于贝叶斯确证网络模型中的参数设置，基本是按照贝叶斯确证模型的思路，给出符合主观信念的条件概率即可。

在这3种连接模式及主观概率参数的基础上，就可以根据假说与证据的逻辑关系构建出一个完整的贝叶斯确证网络模型。

在贝叶斯因果网络中，它的推理主要有正向和反向两种(图3)。基于贝叶斯网络所蕴涵的因果关系解释，正向推理其实也就是从原因推导结果的因果推理，反向推理则是从结果追溯原因的诊断推理。推理的结构在图中是不会直接揭示的，而是根据整个系统的语义设置和研究的需要而形成某种特定的形式与内容。

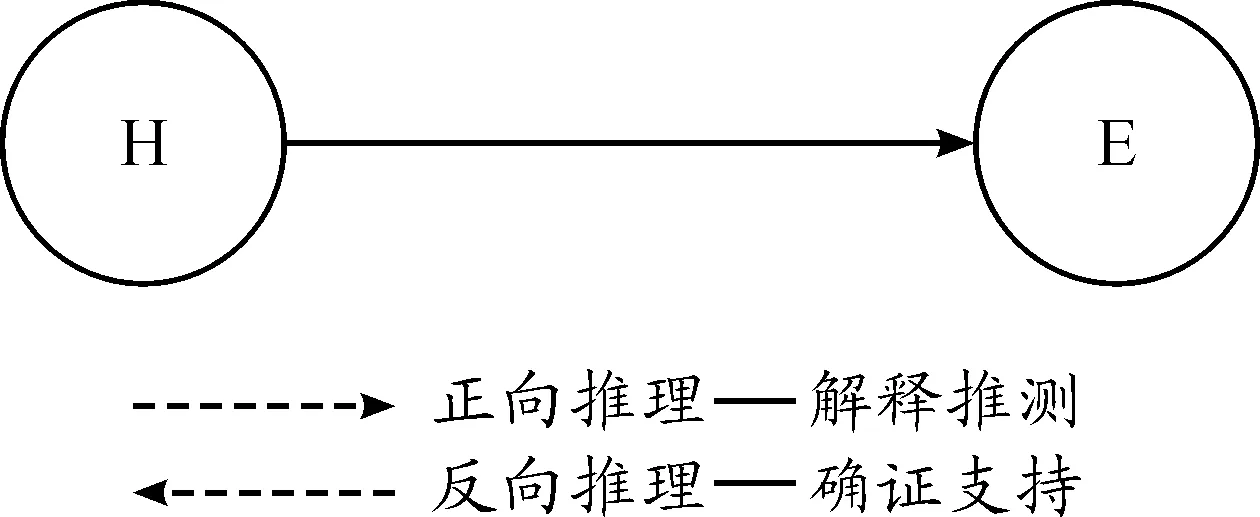
图3　确证网络中的两种推理

对于贝叶斯确证网络而言，由于它所承担的语义解释是科学检验的解释，所以假说与证据间的相互关系也就表现为假说对证据的解释、推断以及证据对假说的确证、支持，因而网络中的推理也就不再是因果性质的。具体而言，在贝叶斯确证网络中的正向推理体现的是从假说到证据的解释、推断过程，反向推理体现的是从证据到假说的确证、支持过程，也有一定的概率依赖语义，但其实质是考察证据的观察结果在多大程度上支持假说，给予它多高的确证度。

就本文的研究目的而言，我们主要关注这个网络中的反向推理，即在给定初始值和相关条件概率的情况下计算假说的后验概率，这与贝叶斯确证模型的确证思路是一样的。而正向推理的结构说明的是科学解释的逻辑。

图4　基于假说演绎模型的简单贝叶斯网络

这样一来，我们就得到了一个单假说、单证据条件下简洁但却完整的贝叶斯确证网络模型。如此，不仅具备合理的网络结构与概率参数，而且可以进行相应的确证推理与逻辑运算。

五、 基于贝叶斯确证理论的复杂贝叶斯网络

对于多个假说，甚至多个证据，依据同样的原理也可以构造假说确证的贝叶斯网络。以历史上对于光的本质的两种假说即波动说(H1)和微粒说(H2)为例，我们选择一些与两种假说相关联的证据。波动说可以用来解释光的衍射E1、双缝干涉实验E2以及光的反射E3，它们三者之间彼此无关；而微粒说则可以解释光的反射E3、影子E4、光粒子E5和光的直线传播E6，它们彼此之间也无关联。这其中两个假说是相互竞争独立的关系，证据之间是相容且独立的关系，假说与证据间可以用有向弧表示出条件依赖关系。根据联合概率的链式规则以及条件独立性，用全联合概率分布来表达它们的关系也就是：Pr(H1,H2,E1,E2,E3,E4,E5,E6)=Pr(H1)Pr(H2)Pr(E1/H1)Pr(E2/H1)Pr(E3/H1,H2)Pr(E4/H2)Pr(E5/H2)Pr(E6/H2)。

根据前文描述的方法，构造的相关贝叶斯网络，如图5。

图5　光的本质的两种假说及其相关证据的

六、结语

作为概率论、因果推理、图论相结合的科学成果，贝叶斯网络确有其独特的魅力与包容性。本文的结构建模只是初步性的尝试，是基于确证理论知识的两种基本结构形式，对于更加复杂多元的确证问题，可能还需要构建更加有效的网络结构。但通过这样的工作已经不难看出，将贝叶斯网络注入到科学确证理论的新鲜血液给确证理论带来深远蓬勃的生命力，给确证理论的表示方式和推理模型都带来极大的更新。相比于之前的确证理论模型，贝叶斯确证网络模型有不少优点和潜力。

首先是图形表达方式带来的可视化、模型化效果。确证理论中的知识与变量本身是多元且互动的，数据结构也有一定的复杂度，在文字语言中很难被简单化处理。确证网络通过有向无环图的形式把这些知识、数据统一在网络模型中，自然而贴切地蕴涵了结点变量之间的确证关系。

其次，确证网络还解决了不确定性知识处理与复杂性的问题。使得确证理论的模型不仅具有确证推理的能力，还揭示了科学解释、推断的逻辑；同时可以利用独立性原则分解全联合分布，根据网络参数进行局部模块处理，降低了系统的复杂度，使得网络可以处理诸如多假说多证据之类的较复杂问题。

再次，确证网络不仅具有科学检验的语义，也具有一定的因果和信念度语义，使得网络可以基于专家知识和新增信息对网络的结构和参数进行学习，也保障了确证的结构和数据随着科学检验的实践而不断修正。

最后，确证网络的构建使得确证理论的形式化进入一个新阶段。它在图论和贝叶斯定理框架下具有规范的建模方法和推理算法，可以通过计算机技术实现程序化。这也就意味着我们可以用更精确的形式化方法来刻画确证知识的表达和推理，并借此处理大型确证问题，同时也为确证网络的应用提供了可能。

参考文献：

[1]张大松.科学确证的逻辑与方法论[M].武汉：武汉出版社，1999.

[2]GLYMOUR C.Theory and evidence[M].Princeton：Princeton university press，1980：12.

[3]艾耶尔A J.语言、真理与逻辑[M].尹大贻，译.上海：上海译文出版社，2006：8.

[4]HEMPEL C G. Studies in the logic of confirmation,aspects of scientific explanation[M].New York:The Free Press,1965：26.

[6]陈晓平.贝叶斯方法与科学合理性——对休谟问题的思考[M].北京：人民出版社，2010：100.

[7]PEARL J.Fusion，propagation，and structuring in belief networks[J].Artificial intelligence，1986(29)：241-288.

[8]姜江，陈英武，常雷雷.证据网络推理学习理论及应用[M].北京：科学出版社，2013：29-31.

[9]SPOHN W.Bayesian nets are all there is to causal dependence[M]//Stochastic causality.stanford:CSLI publications，2001：157-172.

[10]PEARL J.Probabilistic reasoning in intelligent systems：networks of plausible inference[M].San Mateo，California：Morgan Kaufmann，1988：116-122.

(责任编辑张佑法)

Bayesian Network Model of Scientific Confirmation

ZHANG Shun

(Department of Philosophy, Nanjing University. Nanjing 210023, China)

Abstract:The two classical confirmation theories-hypothetico-deductivism and Bayesian confirmation model respectively embody the connotation of qualitative confirmation and quantitative confirmation. However, scientific confirmation is an issue with complex content in its all directions. The two models fail to conquer the complexity and nonmonotonicity of the theory itself. This paper attempts to apply the Bayesian network method to the construction of confirmation theory. The combination of graph theory and Bayesian confirmation theory opens up a new research pathway of confirmation theory. Meanwhile, this paper tries to construct simple models of Bayesian confirmation network and elaborates this network’s basic content in terms of its definition, structure modeling, reasoning etc.

Key words:scientific confirmation; Bayesian confirmation; Bayesian confirmation network

收稿日期：2016-01-08

基金项目：国家社会科学基金项目“归纳悖论与确证逻辑新探”(11BZX061)；江苏省社会科学基金项目“形式知识论研究”(10ZXC009)

作者简介：张顺(1992—)，男(苗族)，重庆黔江人，硕士研究生，研究方向：现代逻辑与逻辑哲学。

doi:10.3969/j.issn.1674-8425(s).2016.06.003

中图分类号：B81

文献标识码：A

文章编号：1674-8425(2016)06-0014-07

引用格式：张顺.科学确证的贝叶斯网络模型[J].重庆理工大学学报(社会科学)，2016(6):14-20.

Citation format：ZHANG Shun.Bayesian Network Model of Scientific Confirmation[J].Journal of Chongqing University of Technology(Social Science)，2016(6):14-20.