基于最大Lyapunov指数的金属疲劳损伤过程研究
刘永坚,黄振峰,2,毛汉领,2
(1.广西大学广西制造系统与先进制造技术重点实验室,广西 南宁530004;2.广西大学机械工程学院,广西 南宁530004)
基于最大Lyapunov指数的金属疲劳损伤过程研究
刘永坚1,黄振峰1,2,毛汉领1,2
(1.广西大学广西制造系统与先进制造技术重点实验室,广西 南宁530004;2.广西大学机械工程学院,广西 南宁530004)
摘要:建立一种基于混沌特征演化分析的金属疲劳损伤过程的监测方法,通过计算金属疲劳损伤过程声发射信号的混沌特性参数分析其疲劳损伤程度。利用声发射技术采集了金属在不同疲劳损伤阶段的声发射信号。采用C-C法计算了金属在不同疲劳损伤阶段声发射时间序列的延迟时间和嵌入维数,然后进行相空间重构。计算金属在不同时间段声发射时间序列的最大Lyapunov指数,分析结果表明:金属在不同疲劳损伤阶段声发射时间序列具有混沌特征,最大Lyapunov的变化趋势与金属疲劳损伤程度具有一定的关联,用混沌理论可以较好的揭示金属疲劳损伤过程的动力学特性,这为金属疲劳损伤程度的在线监测及预测提供了新思路、新方法。
关键词:声发射;疲劳损伤;相空间重构;最大Lyapunov指数
金属材料或构件在服役过程中,容易产生疲劳裂纹,在交变应力的作用下,疲劳裂纹不断扩展,最终导致疲劳断裂。断裂一旦发生,可能会带来灾难性的后果。因此,研究金属疲劳损伤过程并对其进行在线监测和损伤诊断具有重大的现实意义和经济价值。结构在裂纹萌生、扩展和断裂的过程中会释放出瞬态弹性波,声发射技术正是利用高灵敏度的传感器采集了瞬态弹性波引起的表面结构的振动,并将其转化为电信号,信号经过处理和分析得到缺陷的相关信息。目前,大量的学者利用声发射技术对金属材料的损伤过程进行了研究。实践证明,金属疲劳损伤过程的声发射信号表现出很强的非平稳、非线性特性。近年来,主要是利用模态声发射、小波分析以及神经网络等方法处理和分析声发射信号,虽然取得了较好的效果,但是这些方法在处理非线性的声发射信号上具有一定的局限性。
随着混沌理论的发展,许多混沌的特征量已经被广泛应用于机械设备故障诊断中。如关山等[1]提取了刀具磨损过程声发射信号的关联维数、最大Lyapunov指数和Kolmogorov熵三种混沌特征量,结果表明,这三种混沌特征量与刀具磨损状态具有明显的对应关系,实现了对刀具磨损状态的在线监测;姚晓山等[2]采集了齿轮裂纹的声发射信号,利用频谱分析和混沌弱信号检测法对声发射信号进行分析,结果表明混沌弱信号检测法相比于比频谱分析,其精度更高,抗干扰能力更强;王炳成等[3]提取了旋转机械不同故障信号的关联维数、Lyapunov指数、复杂度和近似熵四个混沌特征量,并将这四者融合,提出了非线性度的概念,结果表明,非线性度可以识别旋转机械不同故障状态;赵先进等[4]采用相图分析、最大Lyapunov指数分析以及主成分分析等方法分析了柴油机表面振动加速度信号,结果表明,混沌理论方法可以准确识别柴油机不同故障状态。虽然很多学者将混沌理论应用于机械设备故障诊断中,但是混沌理论用于金属疲劳损伤程度的识别却很少见到报道。
本文将混沌理论应用于金属疲劳损伤程度的识别中,采集了金属三点弯曲疲劳加载过程的声发射信号。对金属不同疲劳损伤阶段声发射时间序列进行相空间重构,绘制了相空间轨迹图,计算了不同疲劳损伤阶段声发射时间序列的最大Lyapunov指数,探索混沌特征量与金属疲劳损伤程度的内在联系。
1 混沌理论
1.1相空间重构
相空间重构是非线性时间序列混沌分析的基础,其基本思想是:对于状态空间中的一个变量,将其在某个延迟时间点上的测量作为新的维数处理,它确定了状态空间中的一点。按照这个过程重复进行测量不同时间的延迟量,就得到许多这样的点,即可重构出与原系统拓扑等价的状态空间。
设时间序列x(t),t=1,2,…,n,重构相空间为:
X1=[x(1),x(1+τ),…,x(1+(m-1)τ)]
X2=[x(2),x(2+τ),…,x(2+(m-1)τ)]
…
其中:m为嵌入维数,τ为延迟时间,M为相空间重构的个数,M=n-(m-1)τ.
相空间重构的重点在于延迟时间和嵌入维数的选择,延迟时间和嵌入维数太大或者太小,都会使得重构后的相空间轨迹模糊不清,失去原来系统的动态特性。因此延迟时间和嵌入维数的选取至关重要。
1.2延迟时间和嵌入维数的求取
目前,延迟时间和嵌入维数的选取有很多种方法。不同的方法都有其特点,也有一定的局限性。本文选取了C-C法[5]同时求取延迟时间和嵌入维数,步骤如下:},重构相空间,X=Xi{ }该时间序列的关联积分为:}分解成t个不相交的子序列:
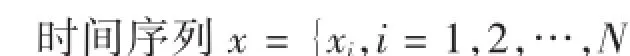

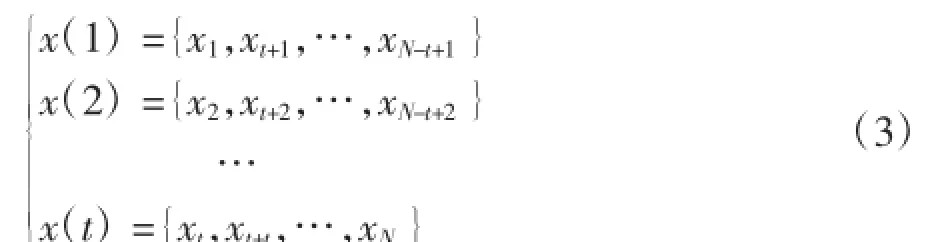
将序列
其中:t为重构时延,N为t的整数倍。
当N→∞时,有:
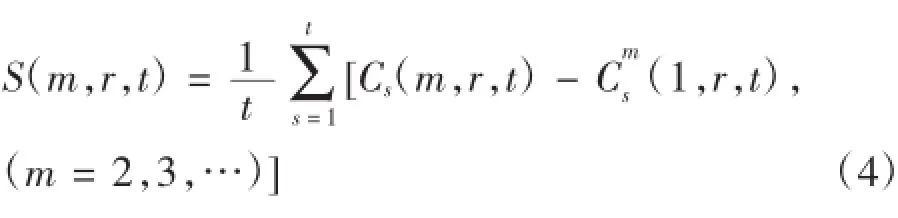
S(m,r,t)最大和最小的差值为:
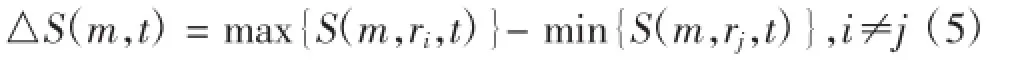
根据经验,m和r的取值范围分别为,2≤m≤5,σ/2≤r≤2σ计算如下方程:
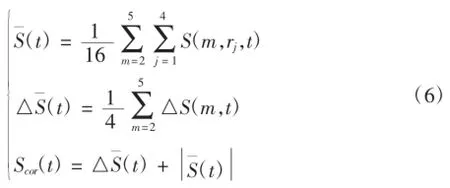
画出三个变量随时间t的函数图像,则延迟时间τ为△S-(t)的第一个极小值,嵌入宽窗τw为Scor(t)的最小值,由τw=(m-1)τ求出嵌入维数m.
1.3最大Lyapunov指数的计算
Lyapunov指数描述了系统在相空间中两个相距较近的轨道收敛或发散的平均指数率[6]。最大Lyapunov指数大于0时,说明系统具有混沌特性。本文采用小数据量法计算了最大Lyapunov指数[7]。步骤如下:
寻找参考相点在相空间内的最近邻点,其轨道的距离为初始距离:
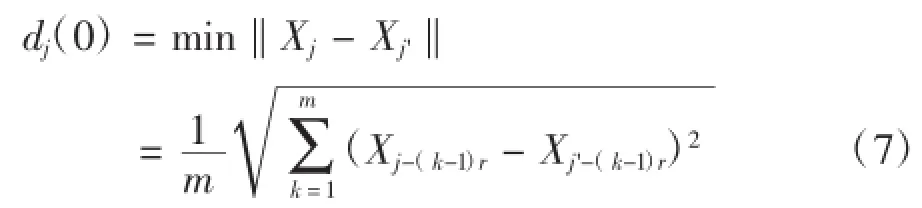
随着时间的演化,初始距离经过s个采样时间步长后,其距离变为:
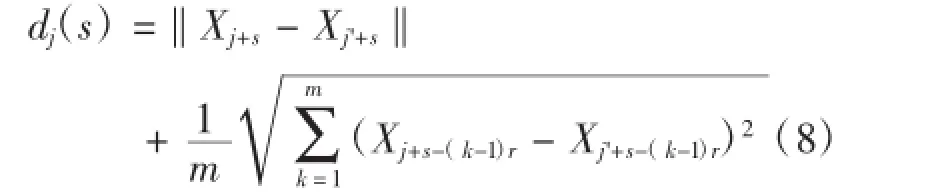

用最小二乘法拟合线性关系较好的区间的斜率就是最大Lyapunov指数。
由于参考点与最近邻点具有指数分散率,所以两边取对数化简可得:

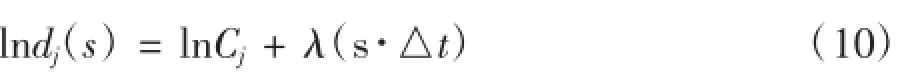
求出的lndj(s)平均值y(s)
2 试验过程
2.1疲劳试验声发射信号采集
根据GB4161-84加工出45号钢三点弯曲试样,长、宽、高分别为L=120 mm,B=15 mm,W=30 mm.在试样中间用线切割技术加工出一条预制的机械缺口。
试验现场图如图1所示,疲劳试验机为PX-20高频疲劳试验机,频率设置为自适应频率,声发射仪的型号为PCI-2,采样频率为1 MHz,增益40 dB,采集45号钢疲劳试验整个过程的声发射信号。

图2为采集到的裂纹萌生阶段、裂纹缓慢扩展阶段、裂纹快速扩展阶段、临近破坏阶段四种状态的的声发射信号。由图可以看出金属不同疲劳损伤阶段声发射信号的幅值不同,裂纹萌生阶段声发射信号的幅值最小,裂纹快速扩展阶段声发射信号的幅值最大。
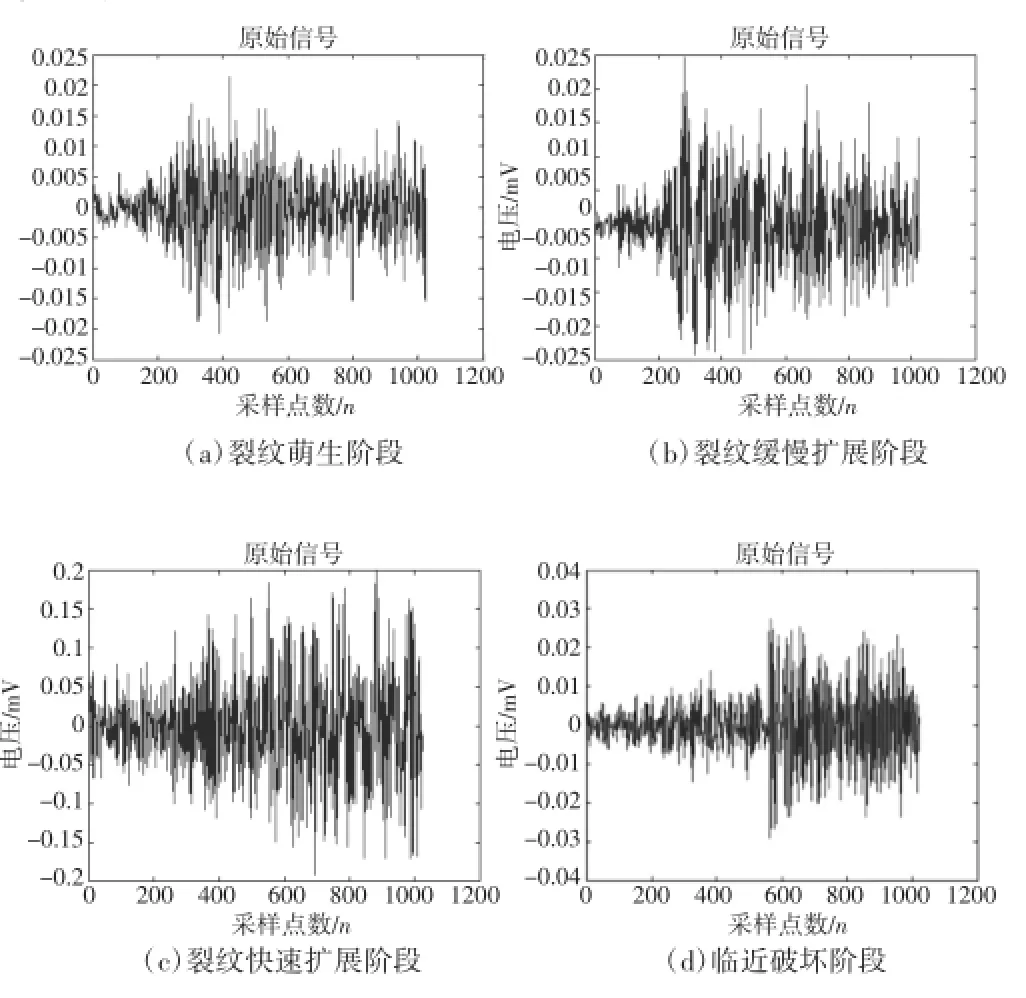
图2 金属不同疲劳损伤阶段的声发射信号
2.2试验结果分析
2.2.1相图分析
采用C-C法分别求取这四个阶段声发射信号的延迟时间和嵌入维数,如图3所示。
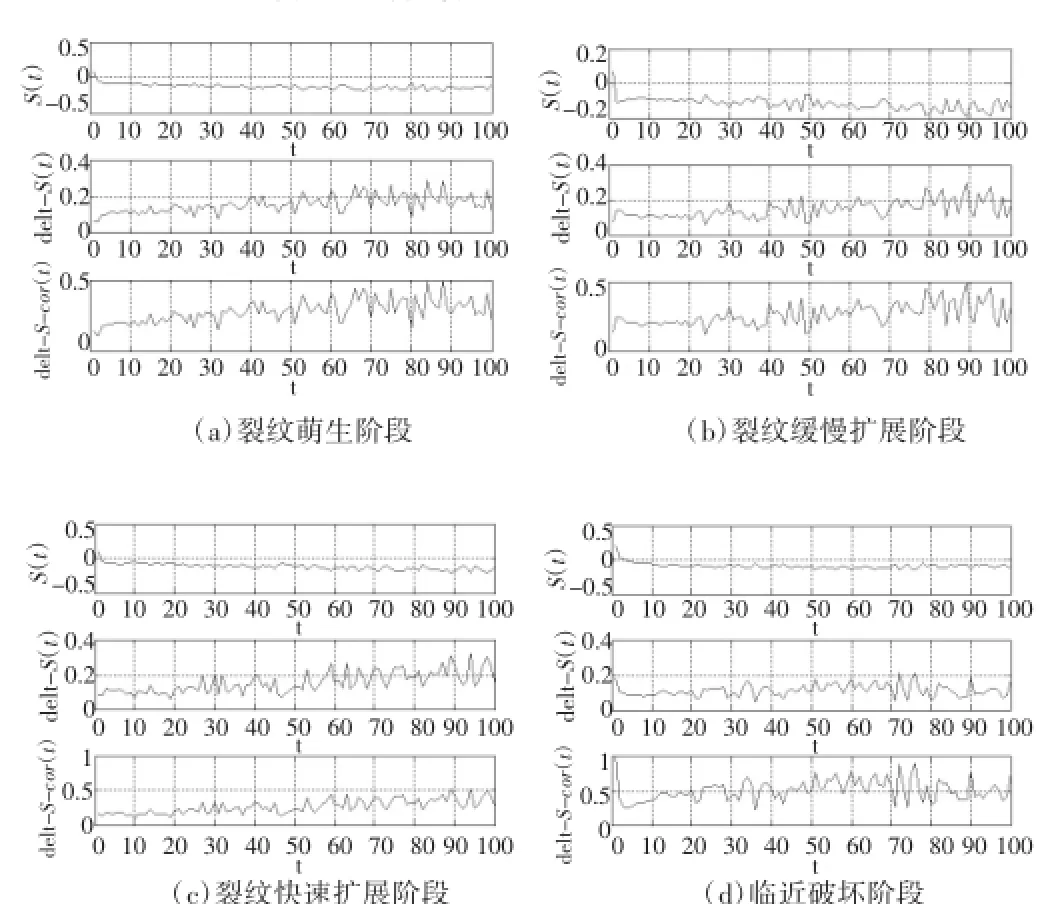
图3 金属不同疲劳损伤阶段C-C法计算结果
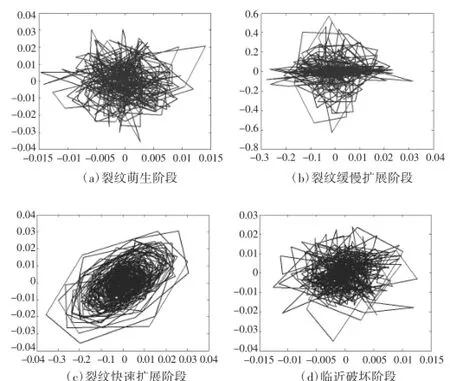
图4 金属不同疲劳损伤阶段相空间轨迹图
由图4可以看出金属不同损伤阶段声发射信号的相空间轨迹图不断扭曲、折叠、拉伸,具有自相似的分型结构,符合奇异吸引子的特点,因此金属疲劳损伤过程声发射信号具有混沌特性。
2.2.2最大Lyapunov指数分析
在金属疲劳损伤过程的不同时间段选取17组数据,计算其最大Lyapunov指数,如图5所示为最大Lyapunov指数的计算结果。
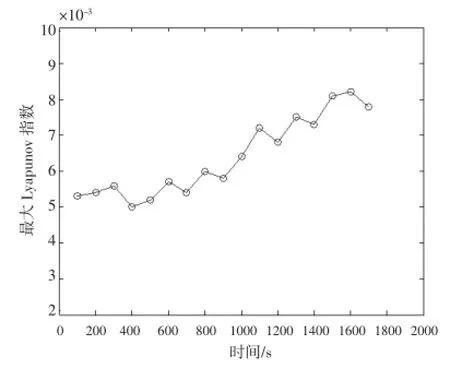
图5 最大Lyapunov指数趋势图
由图5可以看出,金属疲劳损伤过程不同时间段声发射信号的最大Lyapunov指数均大于0,表明声发射信号存在混沌现象。同时,随着金属疲劳损伤的加剧,最大Lapunov指数呈现增大的趋势。最大lyapunov指数的值越大,混沌程度就越高,因此金属疲劳损伤过程声发射信号混沌程度逐渐增强。
在二维空间中重构AE信号的相空间轨迹图,如图4所示。
3 结束语
(1)金属不同疲劳损伤阶段声发射信号的相空间轨迹图存在奇异吸引子,因此金属疲劳损伤过程声发射信号具有混沌特性。
(2)计算了金属疲劳损伤过程不同时间段的最大Lyapunov指数,结果表明,随着金属疲劳损伤程度的加剧,最大Lyapunov指数呈现增大的趋势。最大Lyapunov指数与金属疲劳损伤程度具有明显的对应关系,因此最大Lyapunov指数可以用作金属疲劳损伤状态监测的特征参数。
参考文献:
[1]关山,彭昶.刀具磨损声发射信号的混沌特性分析[J].农业工程学报,2015,31(11):60-65.
[2]姚晓山,张永祥,明廷锋,等.混沌弱信号检测法在齿轮裂纹声发射检测中的应用[J].武汉理工大学学报:交通科学与工程版,2009,33(2):318-320.
[3]王炳成,任朝晖,闻邦椿.基于非线性多参数的旋转机械故障诊断方法[J].机械工程学报,2012,48(5):63-69.
[4]赵先进,徐玉秀.柴油机表面低频振动的状态空间重构及其应用[J].振动、测试与诊断,2008,28(3):259-264.
[5]Kim H S,Eykholt R,Salas J D.Nonlinear dynamics,delay times,and embedding windows[J].Physica D:Nonlinear Phenomena,1999,127(1):48-60.
[6]杨文平,陈国定,石博强,等.基于李雅普指数的汽车发动机故障诊断研究[J].振动工程学报,2002,15(4):476-489.
[7]杨永锋,仵敏娟,高喆,等.小数据量法计算最大Lyapunov指数的参数选择[J].振动、测试与诊断,2012,32(3):371-374.
Research on Metal fatigue Damage Process based on the Largest Lyapunov Exponent
LIU Yong-jian1,HUANG Zhen-feng1,2,MAO Han-ling1,2
(1.Guangxi Key Laboratory of Manufacturing System&Advanced Manufacturing Technology,Guangxi University,Nanning 530004,China;2.College of Mechanical Engineering,GuangxiUniversity,Nanning 530004,China)
Abstract:A method based on several chaotic characteristics were built to monitor the metal fatigue damage process.The degree of metal fatigue damage was analyzed through several chaotic characteristics of the acoustic emission signals during metal fatigue damage.The AE technology was used to collect the acoustic emission signals at different stages of metal fatigue damage.The C-C method was used to calculate the delay time and embedding dimension of the acoustic emission signals at different stages of metal fatigue damage,then reconstructing the strange attractor.The largest Lyapunov exponent of the acoustic emission in different periods during metal fatigue damage was calculated,the result shows that the chaotic phenomenon exits in acoustic emission signals at different stages of metal fatigue damage.Also the trend of the largest Lyapunov exponent has some association with metal fatigue damage.It was also demonstrated that the dynamic characteristics during metal fatigue damage can be revealed by chaotic theory.It is a new idea for online monitoring and prediction of fatigue damage by analyzing the acoustic emission signal.
Key words:acoustic emission;fatigue damage;phase space reconstruction;the largest lyapunov exponent
中图分类号:TG115.28
文献标志码:A
文章编号:1672-545X(2016)03-0005-04
收稿日期:2015-12-04
基金项目:国家自然科学基金(51365006,51445013)及广西制造系统与先进制造技术重点实验室课题(14-045-15S05)项目。
作者简介:刘永坚(1990-),男,广西贵港人,硕士研究生,研究方向:机电一体化。

