谈高考解题中几种常见的数学思想
兰鹏

摘要:高考数学教学大纲中明确指出,数学知识中的数学思想和方法的测试是对数学一个更高的水平测试的抽象和概括。在近几年的高考试题中不难发现,每年的数学试题主要内容就是对函数和方程、数形结合、分类讨论等数学思想的考查。对此,本文围绕近几年的高考试题进行研究,对高考解题中常见的几种数学思想进行分析和探讨。
关键词:高考解题;数学思想;分类讨论
中图分类号:G633.6 文献标识码:B 文章编号:1672-1578(2016)05-0157-01
将生活当中的现象通过科学的、逻辑的、客观的以及可重复的方法描述各种生活现象的语言就是数学。用数学语言描述生活具体事物的想法就叫做数学思想,数学语言虽然抽象,但却简练。因此,在高考数学考试时,结合数学知识,通过测试的考生反映的数学知识,从学生对数学思想价值观念的理解和整体意义出发,对数学思想和方法进行理解和掌握,注重转换方法,淡化其他的一些特殊技巧,可以科学的检测出学生对高中数学知识当中所蕴含数学思想以及方法的掌握情况。
1.函数与方程
函数是指在一个变化的过程当中,假如有两个变量x、y,如果给定一个x值都有唯一的一个y与其相对应,那么就称这个y是这个x的函数。函数思想就是利用变化的特点,分析和探究数学中数变化的关系,从而构建函数,并且运用函数的性质和特点去解决实际的问题。方程是指两个数学式之间具有相等关系的一种等式。方程思想就是分析和探究数学各个变量之间的等量关系,构建方程或者是方程组,并且利用方程的性质和特点去解决等量关系。函数与方程的数学思想主要就体现在两大方面:第一种建立函数,进行化简,第二种就是求值、证明不等式、参数取值范围以及解方程组。函数与方程可以相互转化,互相解决,函数可以解方程,方程也可以界函数,这是历年高考的必考题,因此,需要学生在解题时一定要注意函数与方程之间的转化,要学会相互利用[1]。
例如:(1)函数与方程的密切关系:对于函数式y=f(x),当y=0时,就可以将其转化为方程来表示f(x)=0,当然也可以将函数式y=f(x)转换成方程式为y-f(x)=0。
(2)函数与不等式:对于函数式y=f(x),当y<0时,转化成不等式为f(x)<0,当y>0时,转化成不等式为f(x)>0。根据函数图像来解决相关方成问题。
(3)在立体几何中,有关计算角、面积、线段等问题需要函数与方程的方法进行解决。
2.数形结合
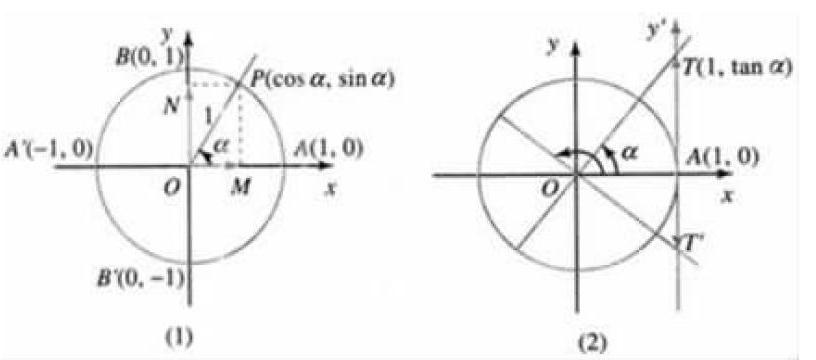
数形结合的数学思想是基于数与形之间的关系,通过数与形的相互转化进行解决数学难题,是解决数学问题的重要途径。数形结合思想通过"以形助数"使复杂的问题转换简单化,将抽象的问题转为具体化,将抽象思维可以改变形象思维,科学有效的掌握数学知识中的本质问题,充分体现了数学的灵活性和规律性。数形结合通常的表现形式为:①实数与数轴上的点的对应关系;②函数与图象的对应关系;③曲线与方程的对应关系;④以几何元素和几何条件为背景建立起来的概念,如复数、三角函数等;⑤所给的等式或代数式的结构含有明显的几何意义[2]。数形结合的方法是高中解决数学难题是最常用的方法之一,方法简单,并且学生都容易接受。例如:《任意三角函数》中,任意角的三角函数定义:sinα=yr,cosα=xr,tanα=yx。单位圆与三角函数线中,单位圆与三角函数线定义:如图(1)所示,PM表示α角的正弦值,叫正弦线,OM表示α角的余弦值,叫余弦线。如图(2)所示,AT表示α角的正切值,叫正切线。图中的线段长度就是三角函数值的大小,图中线段方向所表示的就是三角函数值的正负。
数形结合的解题思想是高中数学解决难题的方法之一,通过数形结合,不仅至关,而且还很容易发现正确的解题思路,帮助学生更好更快的解决问题,避免了复杂繁琐的解题过程,化简了解题思路和方法。数形结合是历年高考的必考题型之一,因此,学生要熟练掌握数形结合的解题方法,并且合理运用,解决数学难题。
3.分类讨论
分类讨论就是当问题所给的对象不能统一研究时,需要根据每个类别的标准分类进行研究,然后对每一类进行归纳总结,最后综合得出所有问题的答案。实际上就是将数学难题化整为零,然后各个击破,最后再进行总结。分类讨论的原则是:在保证分类科学的前提下,标准统一,要做到不重复,不遗漏,并且力求最简。分类讨论的方法:首先要明确讨论的对象以及对象的全体,经对象进行分类,然后再逐一分析和讨论,最后归纳、总结[3]。例如:在求函数最大值、最小值中,假设函数f(x)=x2+|x-a|+1,x∈R,求函数f(x)的最小值。那么解这道数学题时就可以分类讨论了:
分类讨论的方法是高中解决数学难题是最常用的方法之一,并且也是高考中必考的数学解题方法之一,可以帮助学生将难题分类解决,然后进行归纳和总结,最终解决数学难题。
结语:综上所述,想要学好数学,就需要具备宽阔的数学思想,数学思想是对数学知识的最高水平、高层次的总结和概括,是一种对数学知识和技能的"悟性",掌握数学思维的最高水平就是解决问题的能力,无意识的地自然反映出解题的方法,这是高考的核心。数学思想不是凭空想象的,是根据很多经验和实践的总结和而得来的,学生应该多进行实践然后总结和归纳,进一步提升数学思想。
参考文献:
[1]周寿明.微分中值定理教学中的几种辅助函数的构造[J].东莞理工学院学报,2013,03:128-130.
[2]左飞.例谈微分中值定理中辅助函数的构造方法[J].科技信息(学术研究),2014,21:399+401.
[3]吕亚芹.培养学生数学思维能力的研究和探索[J].北京建筑工程学院学报,2014,01:72-75.

