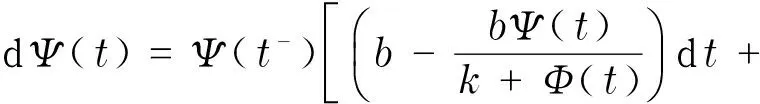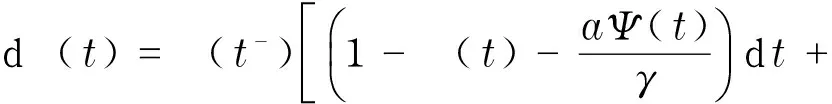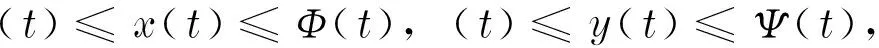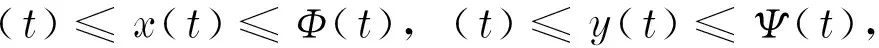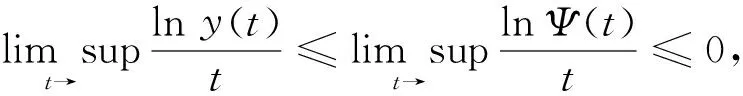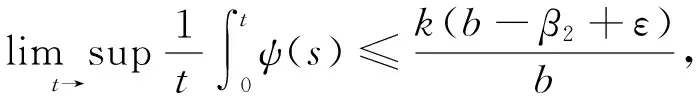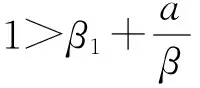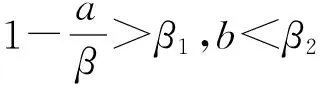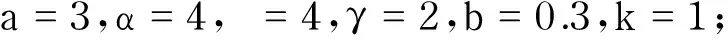具有Levy噪声的随机Holling-Tanner模型

周艳丽,　璞桂萍

(1.上海健康医学院 文理学院,上海　200093; 2.上海健康医学院 健康信息技术与管理学院,上海　200093)



具有Levy噪声的随机Holling-Tanner模型

周艳丽1,璞桂萍2

(1.上海健康医学院 文理学院,上海200093; 2.上海健康医学院 健康信息技术与管理学院,上海200093)

摘要：考虑了噪声对随机Holling-Tanner模型的影响.这种噪声可以理解为海啸、地震、大规模的传染病等产生的突发的且随机性很强的干扰.首先,证明了该模型的全局正解的存在唯一性.然后,结合随机比较定理和鞅论等知识找到了种群在时间均值意义下持续存在和随机灭亡的充分条件.这些结论说明Levy噪声对种群的持久性和灭绝性具有显著性的影响,甚至可以使种群的长期动力学行为发生根本性改变.最后,通过数值模拟直观地验证了Levy噪声对种群的影响.

关键词：Holling-Tanner模型; Levy噪声; 持续; 绝灭

由于生物种群模型理论对于实际应用的重要指导意义和价值,这方面的研究越来越受到重视.在自然环境中存在着大量的不确定的随机因素,这些不确定的因素对生物种群模型有着明显的影响.因此,考虑随机生物种群模型能更客观、更全面地了解和认识生物的发展规律和内在本质.近些年来,许多学者将确定性的生物种群模型推广到随机的生物种群模型上,并取得了丰富的研究成果，如环境噪声无论多么小都可以抑制随机种群模型的爆破,模型解的长期行为持久性、非持久性、遍历性、平稳分布等[1-12].

文献[1-12]提到的随机生物种群所受的环境噪声都是高斯白噪声干扰的结果.高斯白噪声是用来描述一类比较平稳的、连续的随机干扰.事实上,在生态生物系统中,由于洪水的泛滥、海啸、大规模的传染病、地震、大旱、火山爆发、气候变暖、股市震荡等产生的是突发的、不连续的、随机性很强的干扰.一旦发生,生物生长的环境就会发生很大的改变,甚至可以导致种群灭绝.此时,若仅仅用单一的高斯白噪声来描述这种突发现象,很难真实地反映种群的变化情况.在生物动力种群中,为了更好地描述现实世界中的随机现象,可以建立带Levy跳的数学模型来描述这种突变现象.

因此,研究带Levy跳的随机生物系统是非常必要的.近几年,已有学者开始关注这种新的激励对随机生物系统的影响[13-17].受以上文献的启发,本文将文献[18]中的模型推广到带Levy跳的随机Holling-Tanner捕食与被捕食模型中.

1模型的建立

在文献[18]中,Khellaf等主要讨论模型

(1)

初值为x(0)=x0>0,y(0)=y0>0.其中,x(t),y(t)分别表示被捕食者和捕食者在t时刻的密度,参数a,b,α,β,γ均为正常数.Khellaf等指出模型(1)存在3个平凡的平衡点

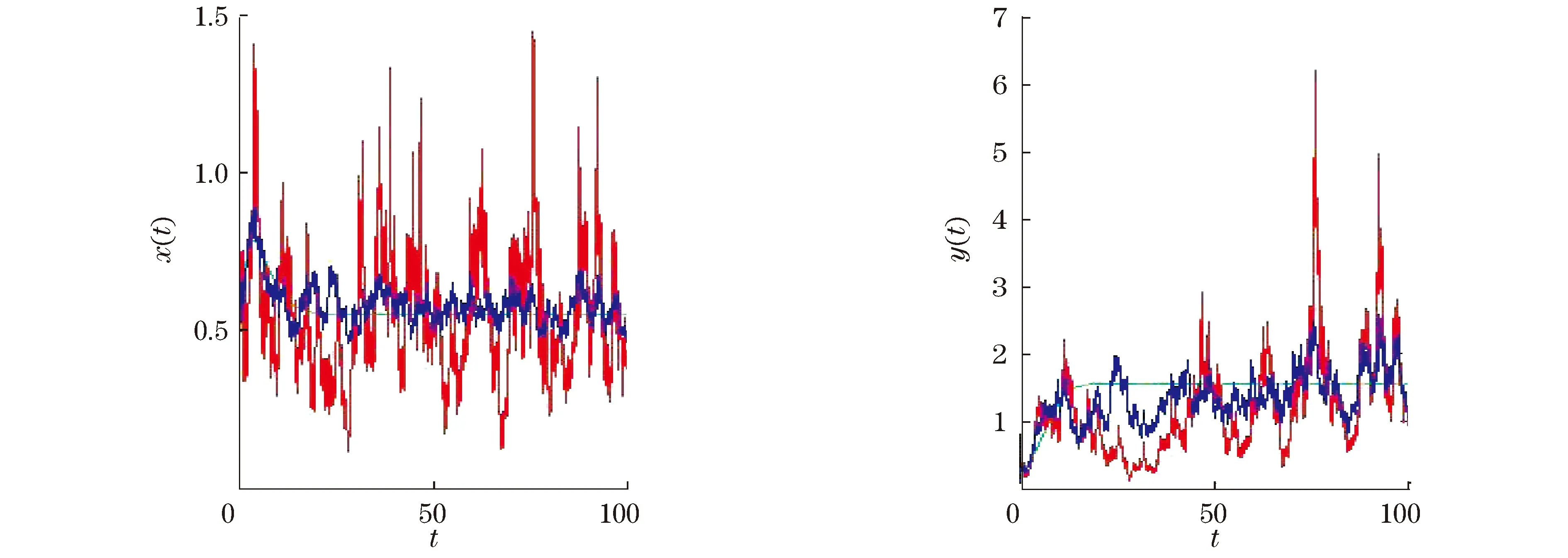
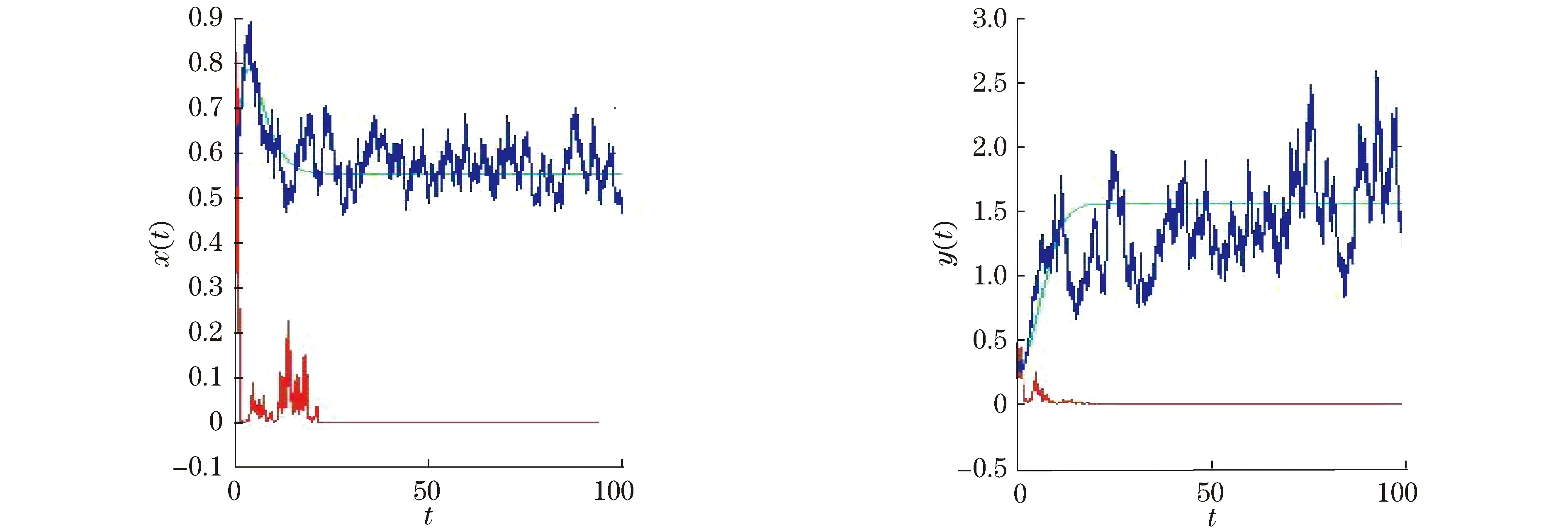
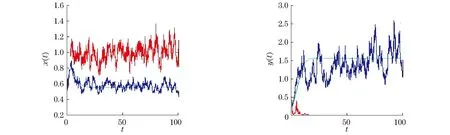
同时,当ak

且y*=x*+k.

Mandal等[12]对模型(1)进行了白噪声干扰,得到与模型(1)相对应的随机模型

(2)

式中：σ1,σ2表示噪声强度;B1(t),B2(t)是定义在完备的概率空间(Ω,{Ft}t≥0,P)上具相互独立的标准布朗运动;{Ft}t≥0是Ω上的一个σ代数且满足通常条件(即右连续,F0包含所有零测集).

文献[2]证明了模型(2)的全局正解存在唯一性、种群的持续存在性、模型存在平稳分布的条件等性质.

在模型(2)的基础上,进一步考虑带有Levy噪声的随机模型,具体模型为

(3)

结合实际生物意义,本文作如下假设:

1+γi(u)>0(i=1,2),u∈Y,对每一个m>0都有Lm>0且满足条件A1和条件A2.

其中,H1(x,u)=γ1(u)x(t-),H2(y,u)=γ2(u)y(t-).

于是

(4)

2模型(3)全局正解的存在唯一性

由于x(t),y(t)分别表示被捕食者和捕食者在t时刻的密度或种群的大小,根据生物实际意义,本文感兴趣的是正解.目前还没看到对于种群随机模型(3) 的研究结果,本文主要研究随机模型(3) 的种群动力学性质,如解的全局正解的存在唯一性、有界性、随机持久及随机灭绝等.

首先,利用变量变换和随机微分方程比较定理、伊藤公式等证明随机模型(3)的全局正解的存在唯一性.

证明考虑方程

(5)

其中

定理1证明了模型(3)存在唯一的局部正解.采用类似于文献[7]的方法,进一步证明此解是全局的,即证明τe=，a.s.

由于模型(3)的解为正,可得

令

(6)

则Φ(t)是

(7)

由随机微分方程比较定理[19]得

由模型(3)的第二式可得

显然

(8)

是方程

(9)

的唯一解,且y(t)≥ψ(t),t∈[0,τe), a.s.

又

则可得

(10)

是方程

(11)

的解.其中

由随机微分方程比较定理[19]得

另外

显然

(12)

是方程

(13)

的解,且满足

综合以上结论,可得

由于φ(t),Φ(t),ψ(t)和Ψ(t)(t≥0)都是全局存在的,故可得定理2.

(14)

3模型(3)解的长期行为

现讨论随机模型(3)的持久性.陈兰荪等[20]给出了确定性系统的时间均值意义下的持续存在的定义.Mandal等[12]类似地给出了随机意义下的种群持续的定义.

定义1[12,21]称种群x(t)在时间均值意义下是持久的,若

为了方便问题的证明,首先引入几个引理.

引理1[16]设x(t)∈C(Ω×[0,+),R+).

a. 若存在正常数T,ρ,ρ0,使得

b. 若存在正常数T,ρ,ρ0,σi(i=1,2),使得

引理2[14]设M(t)(t≥0)是局部鞅,定义

引理3 若1>β1,b>β2成立,则

(15)

由式(15)可以得到如下不等式成立:

将式(16)与式(10)结合，可推出

其中

因此,可得

(17)

根据式(4)可知

由引理2得

(18)

又

结合以上结论可推出

(19)

将式(19)带入到式(17),得

(20)

上式两端同时从0～t积分,并且两端同除以t,得

(21)

由式(18)可知,对于任意ε>0,都存在T,使得

-ε/2≤t-1lnψ(0)≤ε/2,

-ε/2≤t-1k2(t)≤ε/2, t≥T

(22)

成立.

将式(22)代入式(21),可得

t-1lnψ(t)≤b-β2+ε-

(23)

t-1lnψ(t)≥b-β2-ε-

(24)

令ε充分小,使得b-β2-ε>0,由引理1得到

由于ε的任意性,可得

(25)

由定理1的证明过程可知

联立式(20),得

(26)

证明注意到

利用伊藤公式,得

进一步可得

结合引理1、式(8)以及文献[7]中的结论,可得如下结论:当1>β1成立时,有

(27)

证明令V(x(t))=lnx(t),x(t)∈(0,+).对模型(3)的2个方程两边从0～t积分,得

且

定理3的结论说明,模型(3)的Leslie-Gower 项在时间均值意义下是稳定的.

1-β1,a.s.

证明定义V(x(t))=lnx(t),应用伊藤公式,得

且

进一步可得

证明显然,由定理4可得

(28)

定义V(y(t))=lny(t),应用伊藤公式，得

(29)

对式(29)两端从0～t积分,可得

令t充分大,并结合式(18)和引理1的b,可得

(30)

由式(28)和式(30)可知结论成立.

由于x-1-lnx≥0,x>0,则可以推出

若令γi=0,i=1,2,则可以得到文献[12]中的定理5.1的结论.

现给出与以上结论相反的结果.前面主要讨论的是种群的持久性,现给出种群灭绝所需要的条件.

证明a. 对所有t≥0,利用伊藤公式，得

(31)

对式(31)两端同时从0～t积分,可得

进一步化简,得

(32)

又当t充分大时

故当b<β2时,由式(32)得

利用同样的方法可证得

成立,应用引理1,可得

由于ε的任意性,可得

c. 由定理4和a得

从以上结论可知,确定性模型和只有Brown白噪声干扰的随机模型中种群是持续存在的.但是,在Levy噪声干扰下可以导致种群灭绝.

4数值模拟和例子

利用Euler方法[21]对文中的主要结论进行数值模拟分析.在图1～4中,绿线表示确定性模型(1)的解,蓝线表示只有Brown白噪声的随机模型(2)的解,红线表示带有Levy噪声的随机模型(3)的解.图中参数均取为

初值为x0=0.4,y0=0.2.

通过计算可得E*=(x*,y*)=(0.553 1,1.553 1).现通过例子来讨论Levy噪声对种群的影响.

例1取γ1=0.4,γ2=0.3,且由参数取值可得

显然满足

如图1所示,此时x(t),y(t)在时间均值意义下是持续存在的,这与在Brown白噪声的影响结果相同,只是由于Levy噪声的存在使得模型(3)的解围绕内部平衡点E*=(x*,y*)的振幅变大.

图1　a=3,α=4,β=4,γ=2,b=0.3,k=1;σ1=0.1,σ2=0.2,γ1=0.4,γ2=0.3

例2取γ1=1.2,γ2=1.0,简单计算可得

0.02+0.306 9>b=0.3

与例1的结论相反,且满足定理6的a的条件,此时x(t),y(t)均趋于灭绝.图2验证了此结论.如图2所示,尽管在Brown白噪声干扰下x(t),y(t)是持续存在的,但对于模型(3)来说，解趋于0.

例3取γ1=1.2,γ2=0.3,使得满足定理6的b的条件,图3验证了定理6的b的结论,即当条件

例4取γ1=0.1,γ2=1.0,使满足定理6的c的条件,则结论是

也就是说,x(t)具有持久性,而y(t)具有非持久性,即y(t)最终将灭绝，如图4所示.

图2　a=3,α=4,β=4,γ=2,b=0.3,k=1;σ1=0.1,σ2=0.2,γ1=1.2,γ2=1.0.

图3　a=3,α=4,β=4,γ=2,b=0.3,k=1;σ1=0.1,σ2=0.2,γ1=1.2,γ2=0.3

图4　a=3,α=4,β=4,γ=2,b=0.3,k=1;σ1=0.1,σ2=0.2,γ1=0.1,γ2=1.0.

参考文献：

[1]MAOXR,MARIONG,RENSHAWE.EnvironmentalBrowniannoisesuppressesexplosionsinpopulationdynamics[J].StochasticProcessesandTheirApplications,2002,97(1):95-110.

[2]MAOXR,SABANISS,RENSHAWE.AsymptoticbehaviourofthestochasticLotka-Volterramodel[J].JournalofMathematicalAnalysisandApplications,2003,287(1):141-156.

[3]BAHARA,MAOXR.StochasticdelayLotka-Volterramodel[J].JournalofMathematicalAnalysisandApplications,2004,292(2):364-380.[4]MAOXR.Delaypopulationdynamicsandenvironmentalnoise[J].StochasticsandDynamics,2005,5(2):149-162.

[5]MAOXR,YUANCG,ZOUJZ.Stochasticdifferentialdelayequationsofpopulationdynamics[J].JournalofMathematicalAnalysisandApplications,2005,304(1):296-320.

[6]DUNH,SAMVH.DynamicsofaStochasticLotka-Volterramodelperturbedbywhitenoise[J].JournalofMathematicalAnalysisandApplications,2006,324(1):82-97.

[7]JICY,JIANGDQ,SHINZ.Analysisofapredator-preymodelwithmodifiedLeslie-GowerandHolling-typeⅡschemeswithstochasticperturbation[J].JournalofMathematicalAnalysisandApplications,2009,359(2):482-498.

[8]JICY,JIANGDQ,LIXY.Qualitativeanalysisofastochasticratio-dependentpredator-preysystem[J].JournalofComputationalandAppliedMathematics,2011,235(5):1326-1341.

[9]JICY,JIANGDQ.Dynamicsofastochasticdensitydependentpredator-preysystemwithBeddington-DeAngelisfunctionalresponse[J].JournalofMathematicalAnalysisandApplications,2011,381(1):441-453.

[10]JICY,JIANGDQ,SHINZ.Anoteonapredator-preymodelwithmodifiedLeslie-GowerandHolling-typeⅡschemeswithstochasticperturbation[J].JournalofMathematicalAnalysisandApplications,2011,377(1):435-440.[11]MAOXR.Stationarydistributionofstochasticpopulationsystems[J].Systems&ControlLetters,2011,60(6):398-405.

[12]MANDALPS,BANERJEEM.StochasticpersistenceandstationarydistributioninaHolling-Tannertypeprey-predatormodel[J].PhysicaA:StatisticalMechanicsanditsApplications,2012,391(4):1216-1233.

[13]YUANCG,MAOXR.Stabilityofstochasticdelayhybridsystemswithjumps[J].EuropeanJournalofControl,2010,16(6):595-608.

[14]BAOJH,MAOXR,YING,etal.CompetitiveLotka-Volterrapopulationdynamicswithjumps[J].NonlinearAnalysis:Theory,Methods&Applications,2011,74(17):6601-6616.

[15]BAOJH,YUANCG.StochasticpopulationdynamicsdrivenbyLévynoise[J].JournalofMathematicalAnalysisandApplications,2012,391(2):363-375.

[16]LIUM,WANGK.DynamicsofaLeslie-GowerHolling-typeⅡpredator-preysystemwithLévyjumps[J].NonlinearAnalysis:Theory,Methods&Applications,2013,85:204-213.

[17]LIUM,WANGK.StochasticLotka-VolterrasystemswithLévynoise[J].JournalofMathematicalAnalysisandApplications,2014,410(2):750-763.

[18]KHELLAFW,HAMRIN.Boundednessandglobalstabilityforapredator-preysystemwiththeBeddington-DeAngelisfunctionalresponse[J].DifferentialEquationsandNonlinearMechanics,2010,2010:1-24.

[19]PENGSG,ZHUXH.Necessaryandsufficientconditionforcomparisontheoremof1-dimensionalstochasticdifferentialequations[J].StochasticProcessesandtheirApplications,2006,116(3):370-380.

[20]陈兰荪,陈健.非线性生物动力系统[M].北京:科学出版社,1993.

[21]PROTTERP,TALAYD.TheEulerschemeforLévydrivenstochasticdifferentialequations[J].TheAnnalsofProbability,1997,25(1):393-423.

(编辑:石瑛)

Stochastic Holling-Tanner Model with Levy Noise

ZHOU Yanli1,PU Guiping2

(1.College of Arts and Science,Shanghai University of Medicine and Health Sciences,Shanghai 200093,China;2.Faculty of Information Technology and Mangement,Shanghai University of Medicine and Health Sciences,Shanghai 200093,China)

Abstract：The dynamics of stochastic Holling-Tanner model with noises were discussed.The noises can be considered as the flood,tsunami,earthquake,drought,large-scale infectious disease,volcanic eruptions and climate warming etc,and they can produce sudden,discrete and large stochastic perturbations.It is shown that the stochastic Holling-Tanner model with noises admits a unique positive global solution starting from the positive initial value.Then,sufficient conditions of the persistence in the meaning of time average and the extinction of the model were obtained by making use of the stochastic comparison theorem and martingale theory etc.The above conclusions show that Levy noises have significant effects on the persistence and extinction of the population,which can even make the long-time dynamic behavior of the population model change fundamentally.Numerical simulations were carried out to illustrate the influence of Levy noises on the population.

Keywords：Holling-Tanner model; Levy noise; persistence; extinction

文章编号：1007-6735(2016)03-0245-10

DOI：10.13255/j.cnki.jusst.2016.03.007

收稿日期：2015-12-07

中图分类号：O 175.1

文献标志码：A

第一作者： 周艳丽(1976-),女,副教授.研究方向:生物数字.E-mail:zhouyanli_math@163.com