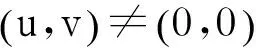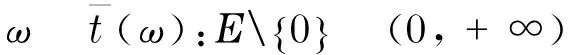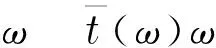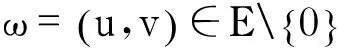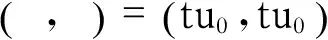分数阶Laplace方程组的山路解

李　青,　魏公明

(上海理工大学 理学院,上海　200093)



分数阶Laplace方程组的山路解

李青,魏公明

(上海理工大学 理学院,上海200093)

摘要：对一类非线性分数阶Laplace方程组Dirichlet问题非平凡解以及正解的存在性分别进行了研究.针对非线性分数阶Laplace方程组在满足Dirichlet边值条件下所具有的特征,通过定义能量空间,然后在该空间中利用Sobolev嵌入定理、控制收敛定理、Brezis-Leb引理,证明分数阶方程组的能量泛函满足Palais-Smale紧性条件,最后利用分数阶Sobolev空间中的山路引理,得出方程组存在非平凡临界点,也即得出这类非线性分数阶Laplace方程组Dirichlet问题存在非平凡解的结论.此外,还利用Nehari流形、极小能量法,通过比较能量法得出一类耦合的非线性分数阶Laplace方程组Dirichlet问题存在正解需要满足的条件,进而得出这类分数阶Laplace方程组存在正解的结论.

关键词：分数阶Laplace算子; 山路引理; Palais-Smale条件; 极小能量解

1问题的提出

运用山路引理[1-4]来证明非平凡解的存在性,是一种很经典的变分方法.本文主要受文献[5]及文献[6]的启发.文献[5]主要针对满足齐次Dirichlet 边值条件的非局部微分方程Lku+f(x,u)=0(x∈Ω)进行了研究.其中

是一个非局部算子.Ω是n中具有Lipschitz边界的有界开集,→(0,+∞)是满足下列性质的函数:

a.γK∈L1(n),其中

其中,s∈(0,1),

本文通过验证该方程能量泛函是否满足Palais-Smale条件,再应用山路引理得出其存在非平凡解.将这种方法运用到如下分数阶Laplace方程组中,即

(1)

不论是在纯理论领域,还是实际生活中,这种分数阶椭圆型算子都有着广泛的应用.它出现在很多不同的背景之下,比如:障碍问题、最优化、金融学、相变、层状材料、反常扩散、晶体错位、半透膜、火焰传播、守恒律、准地转流、多重散射、极小曲面、材料科学、水波等.文献[7]给出了关于分数阶Sobolev空间的清晰而全面的介绍,是学习分数阶Laplace方程极好的参考资料.

文献[6]研究的是如下耦合的非线性薛定谔方程组:

(2)

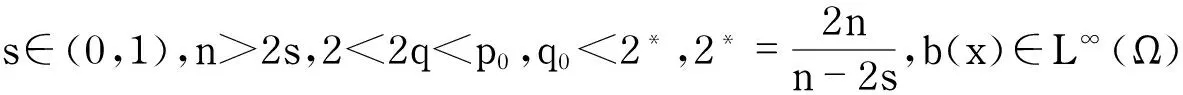
其中,CΩ:=nΩ.

记

E:=X0×X0={(f,g)∈F:对于几乎处处的x∈nΩ有(f,g)=(0,0)}.

其中,

F:=X×X

因为

(3)

所以E和F非空[10].

问题(2)有一个变分结构,实际上它是如下泛函J:E→的Euler-Lagrange方程:

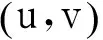
则J的临界点即为问题(2)的解.

(4)

第四部分主要证明方程组(4)向量解的两个分量都是非平凡的,即都是非零的,此时需要对b作一些限制(见推论1).

本文主要结果如下：

推论1假设方程组(4)中b>2q-1-1,2<2q<2*,n>2s,s∈(0,1),则问题(4)存在极小能量解(u,v),其中u>0,v>0.

2一些基本的结论

这部分将证明一些有用的结论.

这里,首先介绍一下空间X和X0的一些基本结论.论文中的一些记法如下:

其中,σ=(CΩ)×(CΩ)⊂2n,CΩ=nΩ.

空间F=X×X的范数定义为

其中,

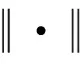
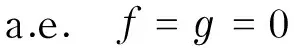
(6)

且

(7)

所以,f,g在n上几乎处处为常数,不妨设f=c∈,g=d∈.

由式(6)可得c=0,d=0,证毕.

下面,G=Hs(Ω)×Hs(Ω)表示分数阶Sobolev空间,并赋予范数

其中

引理1a. 若(u,v)∈F,则(u,v)∈G,且

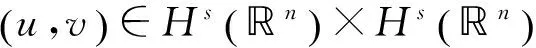
证明a. 若(u,v)∈F=X×X,则

同理

因此,(u,v)∈G=Hs(Ω)×Hs(Ω),

即

b. 由于E={(u,v)∈F:nΩ中几乎处处有(u,v)=(0,0)},因此,若(u,v)∈E,则

且

同理

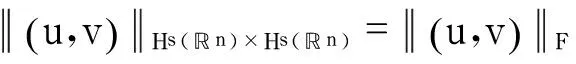
即

引理2存在依赖于n,s,Ω的常数C(n,s,Ω)>1,使得对于任意的(u,v)∈E,有

从而

(9)

是E=X0×X0上和式(5)等价的范数.

证明首先,由式(5)可得

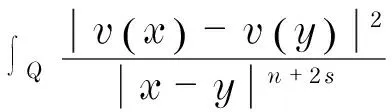
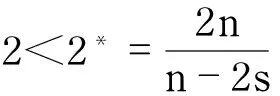
其中,C是仅依赖于n,s的正常数.

因此

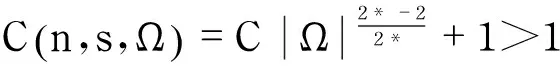
因此

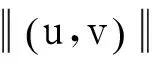
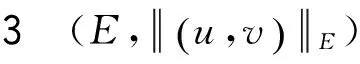
易知〈·,·〉是E上的内积,它对应的范数和式(9)是一致的.

因为L2(Ω)×L2(Ω)是完备的,所以存在(u∞,v∞)∈L2(Ω)×L2(Ω),使得当j→+∞时,在L2(Ω)×L2(Ω)中有ωj=(uj,vj)→(u∞,v∞)成立.因此,存在一个子列(ujk,vjk)⊂E,使得在n中a.e.(ujk,vjk)→(u∞,v∞)[11].

下证(u∞,v∞)∈E.由Fatou引理和式(10)中的第一个不等式(取ε=1),得

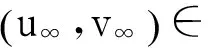
接下来只需证整个序列在E中收敛到(u∞,v∞).为此,令i≥νε,由式(10)的第一个不等式、引理2 及Fatou引理可得

即在E中当i→+∞时,(ui,vi)→(u∞,v∞),引理得证.

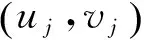
证明由引理1 的b可知(uj,vj)∈Hs(n)×Hs(n).另外,由引理 1 的b以及引理2 可得

其中,C仅依赖于n,s和Ω.因为(uj,vj)在E中有界,所以在G中有界,因此也在L2(Ω)×L2(Ω)中有界,故{uj},{vj}在L2(Ω)中有界.

由文献[7]的Corollary 7.2以及Ω的条件可知,对任意的m∈[1,2*)存在u∞,v∞∈Lm(Ω)和该序列的一个子列(下标仍记为j),使得在Lm(Ω)中,当j→+∞时,uj→u∞,vj→v∞.因为(uj,vj)在nΩ中等于0,所以在nΩ中可以定义(u∞,v∞):=(0,0).因此在Lm(n)中,(uj,vj)→(u∞,v∞).

3山路解的存在性

这部分将利用山路引理来找泛函的临界点.因此,首先需要验证泛函J的几何特征,并且满足PS紧性条件.

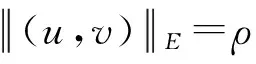
因为

所以

因为Ω有界且2<2q<2*,因此Hs(Ω)连续嵌入到L2q(Ω)中(见文献[5]).因此存在常数C1,C2>0,使得

由引理2可知,存在C′,C″>0,使得

因为2<2q

因此

同理

因为存在常数C4,使得

成立,所以,存在常数C,C*>0,使得

由2<2q

命题得证.

令t>0,有

不妨假设p00,使得

因此

当t→+∞时,存在常数C>0,使得

同样,若q0

命题1和命题2给出了山路引理所满足的几何条件.接下来通过命题3和命题4验证PS条件.

命题3令c∈,是E中的序列,且满足当j→+∞时,

(11)

(12)

可知

对任意j∈N,由式(11)～(12)可知,存在K>0,使得

(13)

(14)

因此

即

(15)

由式(13)和式(15)可得

因为2<2q

因而存在常数K*>0,使得对任意的j∈N,有

命题3得证.

(16)

因为

由式(12)可知

即

同样,

(18)

由引理4,对某子序列,当j→+∞时,(uj,vj)→(u∞,v∞)在Lq(n)×Lq(n)中,(uj,vj)→(u∞,v∞)a.e.在n中.

由控制收敛定理[12]可得

由式(16)、式(18)、式(20)得

即

由式(17)和式(19)得当j→+∞

由Brezis-Leb引理,可知

定理1的证明由命题1～4及山路引理可知,泛函J存在临界点(u,v)∈E,并且

4研究方程组存在正解的条件

特殊地,当p0=q0=2q,b(x)=b时,方程组(2)变为方程组(4)

它对应的泛函J*:E→为

为了研究问题(4)存在正解需要满足的条件,首先给出几个有用的引理.

定义Nehari流形为

是连续的,且映射

定义了E中单位球到N的一个同胚.

证明首先证明泛函J*满足如下的几何性质:

a. (0,0)是一个严格极小值点;

事实上,如果定义

则F满足

由式(21)可推出a成立.由式(22)可知,对任意t>0,下面的不等式成立

因此b成立.

(23)

(24)

因为g的每一个正的驻点t>0满足

记

其中

引理6cN=c1=c.

证明由引理5 可知

注:事实上,下面的证明只需用到c≤c1即可.

(26)

接下来只需证明

因为u0是式(26)的解,所以

因此可以得到如下关系:

(27)

(28)

另外,由引理6 可知

其中,C由式(27)定义.

参考文献：

[1]SERVADEI R,VALDINOCI E.Lewy-Stampacchia type estimates for variational inequalities driven by(non)local operators[J].Revista Matemática Iberoamericana,2013,29(3):1091-1126.

[2]DI Nezza E,PALATUCCI G,VALDINOCI E.Hitchhiker’s guide to the fractional Sobolev spaces[J].Bulletin des Sciences Mathématiques,2012,136(5):521-573.

[3]BREZIS H.Analyse fonctionelle-theorie et applications[M].Paris:Masson,1983.

[4]SERVADEI R,VALDINOCI E.Mountain pass solutions for non-local elliptic operators[J].Journal of Mathematical Analysis and Applications,2012,389(2):887-898.

[5]MAIA L A,MONTEFUSCO E,PELLACCI B.Positive solutions for a weakly coupled nonlinear Schrödinger system[J].Journal of Differential Equations,2006,229(2):743-767.

[6]AMBROSETTI A,RABINOWITZ P.Dual variational methods in critical point theory and applications[J].Journal of Functional Analysis,1973,14(4):349-381.

[7]RABINOWITZ P H.Minimax methods in critical point theory with applications to differential equations[M].Province,RI:American Mathematical Society,1986.

[8]STRUWE M.Variational methods:applications to nonlinear partial differential equations and Hamiltonian systems[M].Heidelberg:Springer-Verlag,1990.

[9]PUCCI P,RADULESCU V.The impact of the mountain pass theory in nonlinear analysis:a mathematical survey[J].Bollettino Dell Unione Matematica Italiana,2010,3(3):543-584.

[10]BREZIS H,LIED E H.Minimum action solutions of some vector field equations[J].Communications in Mathematical Physics,1984,96(1):97-113.[11]RABINOWITZ P H.On a class of nonlinear Schrödinger equations[J].Journal of Applied Mathematics and Physics,1992,43(2):270-291.

[12]陈雨彤,魏公明.具奇异非线性项p-Laplace方程Dirichlet问题解的存在唯一性[J].上海理工大学学报,2015,37(4):311-316.

(编辑:丁红艺)

Mountain Pass Solutions for the System of Equations Driven by the Fractional Laplace Operator

LI Qing,WEI Gongming

(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：The existence of nontrivial solutions and positive solutions for fractional Laplace systems with Dirichlet boundary conditions was investigated.According to the features when the Dirichlet boundary conditions of fractional Laplace systems are satisfied and based on the mountain pass theorem,embedding theorem,dominated convergence theorem and Brezis-Leb lemma in Sobolev space,the Palais-Smale compactness conditions of the energy functional were proved.Then the existence of nontrivial solutions for fractional Laplace systems with Dirichlet boundary conditions was concluded.Moreover,The Nehari manifold and minimal energy method were used to prove the existence of positive solutions for fractional Laplace systems with Dirichlet boundary conditions.

Keywords：fractional Laplace operator; mountain pass theorem; Palais-Smale condition; least energy solution

文章编号：1007-6735(2016)03-0235-10

DOI：10.13255/j.cnki.jusst.2016.03.006

收稿日期：2015-01-08

基金项目：沪江基金资助项目(B14005)

通信作者：魏公明(1974-),男,副教授.研究方向:偏微分方程.E-mail:gmweixy@163.com

中图分类号：O 175.25

文献标志码：A

第一作者： 李青(1991-),女,硕士研究生.研究方向:偏微分方程.E-mail:qinglismile@163.com