首尾差r-循环矩阵的判别方法及逆和广义逆的快速算法

潘　雪,　秦　梅

(上海理工大学 理学院,上海　200093)



首尾差r-循环矩阵的判别方法及逆和广义逆的快速算法

潘雪,秦梅

(上海理工大学 理学院,上海200093)

摘要：提出了一种新的循环矩阵,称之为首尾差r-循环矩阵(简记为FLDcircr矩阵).验证了它的线性运算、矩阵乘积、逆矩阵等仍为FLDcircr矩阵.通过构造基本FLDcircr矩阵,给出FLDcircr矩阵的判别方法及逆和广义逆的快速算法.

关键词：FLDcircr矩阵; 判别法; 对角化; 逆; 广义逆

循环矩阵是矩阵论的重要组成部分,它的特殊结构和性质被广泛应用于应用数学、计算数学及现代工程等领域[1-6],并且不断有新的循环矩阵被提出[7-11].基于上述研究,本文首先给出了FLDcircr矩阵和基本FLDcircr矩阵的概念以及它们的和、差、乘积、逆矩阵和伴随矩阵的性质,然后通过构造基本FLDcircr矩阵,给出了FLDcircr矩阵的5种判别方法,并讨论它的对角化和奇异性,最后给出它的逆和广义逆的快速算法及数值例子[12-13].在本文中,矩阵都是在复数域中讨论的.

1预备知识

定义1对于n阶方阵A,若A具有形状

则称A为n阶FLDcircr矩阵,记作A=FLDcircr(a0,a1,…,an-1)定义2称n阶方阵

为基本FLDcircr矩阵.

D的特征多项式为g(x)=xn+rx-r,且Dn=r(In-D),规定D0=In.

由FLDcircr矩阵的定义易证命题1.

命题1如果A和B都是FLDcircr矩阵,则A+B,A-B以及kA(k为任意常数)都是FLDcircr矩阵.

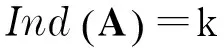
定义4[14]设A∈Cn×n,如果存在X∈Cn×n,使得AXA=A,XAX=X同时成立,则称X是A的自反广义逆,记为A{1,2}.

2FLDcircr矩阵的判别法

定理1A是FLDcircr矩阵当且仅当A有如下形式

(1)

证明由定义1及定义2可证定理1.

定理2A是FLDcircr矩阵当且仅当AD=DA,其中,D为基本FLDcircr矩阵.

证明必要性.因为,A是FLDcircr矩阵,所以,由A和D的定义可得AD=DA.

充分性.由待定系数法可设

由AD=DA可知

以此类推,可得

故A是FLDcircr矩阵.

推论1如果A和B都是FLDcircr矩阵,则AB和BA都是FLDcircr矩阵,并且AB=BA.

证明因为A和B都是FLDcircr矩阵,由定理2可得

AD=DA, BD=DB

因此

ABD=ADB=DAB, BAD=BDA=DBA

所以，AB和BA都是FLDcircr矩阵.

由定理1显然可得AB=BA.

3FLDcircr矩阵的对角化

首先研究基本FLDcircr矩阵D的对角化.

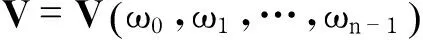
显然V是由ω0,ω1,…,ωn-1构成的非奇异Vandermonde矩阵,且成立

(2)

现研究一般FLDcircr矩阵A的对角化.

由定理1和式(2)可得

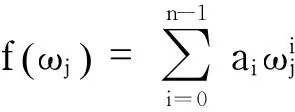
定理3A是FLDcircr矩阵当且仅当V-1AV是对角矩阵.

证明必要性.如果A是FLDcircr矩阵,由上面的讨论可知

充分性.令V-1AV=P1,P1为对角矩阵,则

A=VP1V-1

D=VP2V-1

所以

AD=VP1V-1VP2V-1=VP1P2V-1

DA=VP2V-1VP1V-1=VP2P1V-1

而P1和P2都是对角矩阵,所以,有

AD=DA

因此,A是FLDcircr矩阵.

定理4A是非奇异FLDcircr矩阵当且仅当特征值f(ωi)≠0(i=0,1,…,n-1),其中,ωi(i=0,1,…,n-1)是基本FLDcircr矩阵D的特征值.

4FLDcircr矩阵的逆与广义逆

定理5A是非奇异FLDcircr矩阵当且仅当A-1也是FLDcircr矩阵.

证明必要性.由A是非奇异FLDcircr矩阵及定理2可知

AD=DA

则

所以，A-1是FLDcircr矩阵.

充分性显然.

推论2如果A是非奇异FLDcircr矩阵,则A*也是非奇异FLDcircr矩阵.

定理6设A是FLDcircr矩阵,则A非奇异当且仅当(f(x),g(x))=1.

证明若A是非奇异FLDcircr矩阵,由定理4可知，f(ωi)≠0(i=0,1,…,n-1),所以,f(x)和g(x)没有公共解,即(f(x),g(x))=1.

反之,若(f(x),g(x))=1,则存在u(x),v(x)使得u(x)f(x)+v(x)g(x)=1,故u(D)f(D)+v(D)g(D)=E.由于g(D)=0,f(D)=A,有u(D)A=E.因此,A非奇异且A-1=u(D).由定理1可知,A-1是FLDcircr矩阵.

推论3如果A是非奇异的FLDcircr矩阵,则存在A-1=u(D).

证明由定理6可知,推论显然成立.

证明由A奇异可知(f(x),g(x))≠1.设(f(x),g(x))=d(x),g(x)=d(x)g1(x),f(x)=d(x)f1(x),则(f1(x),g1(x))=1.又g(x)无重根,故(d(x),g1(x))=1,则(d(x)f1(x),g1(x))=1,(d(x)d(x)f1(x),g1(x))=1,即(d(x)f(x),g1(x))=1.

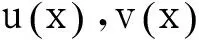
(3)

对式(3)两边同乘f(x),整理得

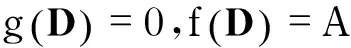
(4)

(5)

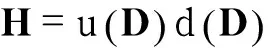
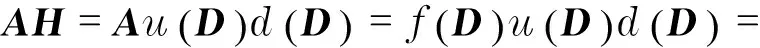
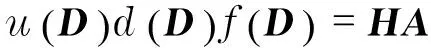
5算法与数值例子

由引理1与推论3的证明,不难得到求FLDcircr矩阵的逆和广义逆的快速算法,其一般步骤如下:

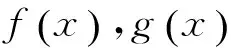
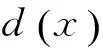
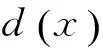
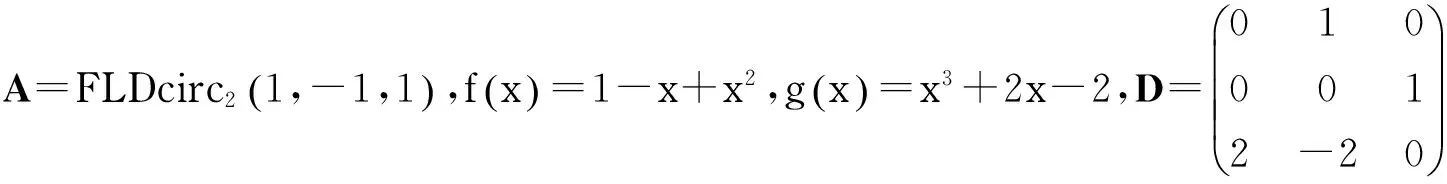
因为

则

所以

即

由步骤3可得

则

所以

即

6结论

提出了FLDcircr矩阵,并验证了它的和、差、乘积、逆矩阵和伴随矩阵仍为FLDcircr矩阵,这充分说明它具有很强的保结构性,这在实际应用中非常重要.通过构造的基本FLDcircr矩阵，给出FLDcircr矩阵的5种判别方法及它的逆和广义逆的快速算法.本文给出的算法将矩阵求逆和广义逆问题转化为多项式计算,降低了问题求解的复杂度,并且FLDcircr矩阵在计算存储时可大量减小存储空间.数值例子表明了算法的可行性.

参考文献：

[1]TOLOMEI P B,TORRES L M.On the first Chvátal closure of the set covering polyhedron related to circulant matrices[J].Electronic Notes in Discrete Mathematics,2013,44(5):377-383.

[2]BOZKURT D,TAM T Y.Determinants and inverses of circulant matrices with Jacobsthal and Jacobsthal-Lucas numbers[J].Original Research Article Applied Mathematics and Computation,2012,219(1/2):544-551.

[3]ZHOU J W,JIANG Z L.The spectral norms ofg-circulant matrices with classical Fibonacci and Lucas numbers entries[J].Applied Mathematics and Computation,2014,233(1):582-587.

[4]WU A G,ZENG X L,DUAN G R,et al.Iterative solutions to the extended Sylvester-conjugate matrix equations[J].Applied Mathematics and Computation,2010,217(1):130-142.

[5]AMDRECUT M.Applications of left circulant matrices in signal and image processing[J].Modern Physics Letters B,2008,22(4):231-241.

[6]SHEN S Q,CEN J M.On the bounds for the norms ofr-circulant matrices with the Fibonacci and Lucas numbers[J].Applied Mathematics and Computation,2010,216(10):2891-2897.

[7]MARRAZZINI C.Characterization of the inverse of a particular circulantt matrix by means of a continued fraction[J].Discrete Applied Mathematics,1980,2(2):163-165.

[8]XU Q Z,LI H Q,JIANG Z L.An algorithm for finding the minimal polynomial of a FLSr-circulant matrix[J].Journal Mathematics (Wuhan),2005,25(6):599-604.

[9]HE C Y,WANG X Y.The discriminance for a special class of circulant matrices and their diagonalization[J].Applied Mathematics and Computation,2014,238(1):7-12.

[10]DAVIS P J.Circulant Matrices[M].New York:Wiley,1979.

[11]SEARLE S R.On inverting circulant matrices[J].Linear Algebra and its Applications,1979,25(1):77-89.

[12]JIANG Z L,XU Z B.Efficient algorithm for finding the inverse and the group inverse of FLSr-circulant matrix[J].Journal of Applied Mathematics and Computing,2005,38(1/2):45-57.

[13]李静,何承源.求解首尾差循环矩阵逆与广义逆的快速算法[J].山东大学学报(理学版),2013,48(6):96-99.

[14]张晓红,蔡秉衡.高等代数专题研究选编[M].西安:西安科学技术出版社,1992.

[15]张凯院,徐仲.数值代数[M].西安:西北工业大学,2000.

(编辑:石瑛)

Discriminance for FLDcircrMatrices and the Fast Algorithm for Their Inverse and Generalized Inverse

PAN Xue,QIN Mei

(Colloge of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：A new type of matrices which is called as the first and the last difference r-circulant matrix (FLDcircr matrix) was presented.The linear operation,the matrix product,the inverse matrix of this type of matrices were verified to be still FLDcircr matrices.Through constructing the basic FLDcircr matrix,the discriminance for FLDcircr matrices and the fast algorithm for their inverse and generalized inverse were provided.

Keywords：FLDcircr matrix; discriminance; diagonalization; inverse; generalized inverse

文章编号：1007-6735(2016)03-0230-05

DOI：10.13255/j.cnki.jusst.2016.03.005

收稿日期：2015-04-10

基金项目：国家自然科学基金资助项目(11426155);沪江基金资助项目(B14005)

通信作者：秦梅(1975-),女,副教授.研究方向:计算数学.E-mail:jisuanusst@126.com

中图分类号：O 151.2

文献标志码：A

第一作者： 潘雪(1990-),女,硕士研究生.研究方向:计算数学.E-mail:xiaoxuehe1126@163.com