剑杆织机柔性从动件共轭凸轮打纬机构动力学分析

金国光， 秦凯旋， 魏 展， 袁汝旺， 周国庆

(天津工业大学 天津市现代机电装备技术重点实验室， 天津 300387 )

剑杆织机柔性从动件共轭凸轮打纬机构动力学分析

金国光， 秦凯旋， 魏 展， 袁汝旺， 周国庆

(天津工业大学 天津市现代机电装备技术重点实验室， 天津 300387 )

针对剑杆织机共轭凸轮打纬机构因自身振动造成筘座角加速度偏差大，降低织造的质量，缩短共轭凸轮寿命的问题，对共轭凸轮打纬机构进行合理化简化后，采用Rayleigh-Ritz法对柔性从动件进行离散化处理，基于Lagrange方程建立了剑杆织机柔性从动件共轭凸轮打纬机构的动力学方程。运用MatLab软件对柔性从动件共轭凸轮打纬机构进行了动力学仿真分析，在仿真过程中通过改变打纬机构的结构参数探索减小打纬机构振动的方法。仿真结果表明，打纬机构在高速运动过程中柔性从动件产生的横向振动会导致筘座角加速度波动明显，提出了通过减小筘座脚质量来减小筘座角加速度偏差和机构振动的方法。

剑杆织机； 打纬机构； 柔性从动件； Lagrange方程； 角加速度； 动力学

剑杆织机[1]具有转速高、精度高、惯性载荷较大的特点，其动力学问题主要存在于开口机构、打纬机构和引纬机构中。共轭凸轮[2-4]是几何锁合型机构，有很高的运动精度，适合高、中型载荷的高速场合，这些优点是利用弹簧力回程的力锁合型凸轮机构所不具备的。目前，越来越多的剑杆织机为了提高转速而广泛使用共轭凸轮打纬机构[5-6]，但是，当凸轮机构高速运转时，由于从动件的惯性力增加以及机构的振动，会引发构件的变形，导致工作端运动规律偏离预定的要求[7]，产生较大的动态偏差，并会进一步加剧机构的振动，缩短凸轮的寿命；因此，共轭凸轮打纬机构动态性能的优劣严重制约着其转速的提高，同时也是制约我国剑杆织机整体性能和效率提升的瓶颈。

对于高速剑杆织机中的共轭凸轮机构，运动学分析与设计已较为成熟[8-10]，但对其动力学性能分析和动力学优化设计的研究仍然十分有限，尤其对高速剑杆织机中共轭凸轮机构的动力学优化设计尚处于起步阶段。为此，本文采用Lagrange方程，结合Rayleigh-Ritz法[11]对从动件进行离散化处理，建立柔性从动件共轭凸轮打纬机构的动力学模型，并对该机构进行动力学仿真和分析，以期为剑杆织机共轭凸轮打纬机构的优化设计提供理论依据。

1 柔性从动件动力学建模

在实际的应用过程中，共轭凸轮、滚子和筘座的刚度远大于摆臂和筘座脚的刚度，三者的变形对工作端的影响很小，故对共轭凸轮打纬机构进行动力学分析时，可将共轭凸轮、滚子和筘座假定为刚性构件[12-14]。

共轭凸轮打纬机构简化模型如图1所示。主凸轮1和副凸轮9绕主轴A回转时，通过滚子2、8带动摆臂3、7和筘座脚4绕摇轴B摆动，使筘座5带动钢筘6完成打纬的往复运动[15]。

注：1—主凸轮；2—滚子；3—摆臂；4—筘座脚；5—筘座；6—钢筘；7—摆臂；8—滚子；9—副凸轮。图1 共轭凸轮打纬机构简图Fig.1 Sketch of conjugate cam beating-up mechanism

共轭凸轮在高速运转时，筘座脚和摆臂的变形不能被忽略，所以将筘座脚和摆臂作为柔性从动件。柔性从动件的变形如图2所示，其中杆1为筘座脚，杆2和杆3为摆臂。

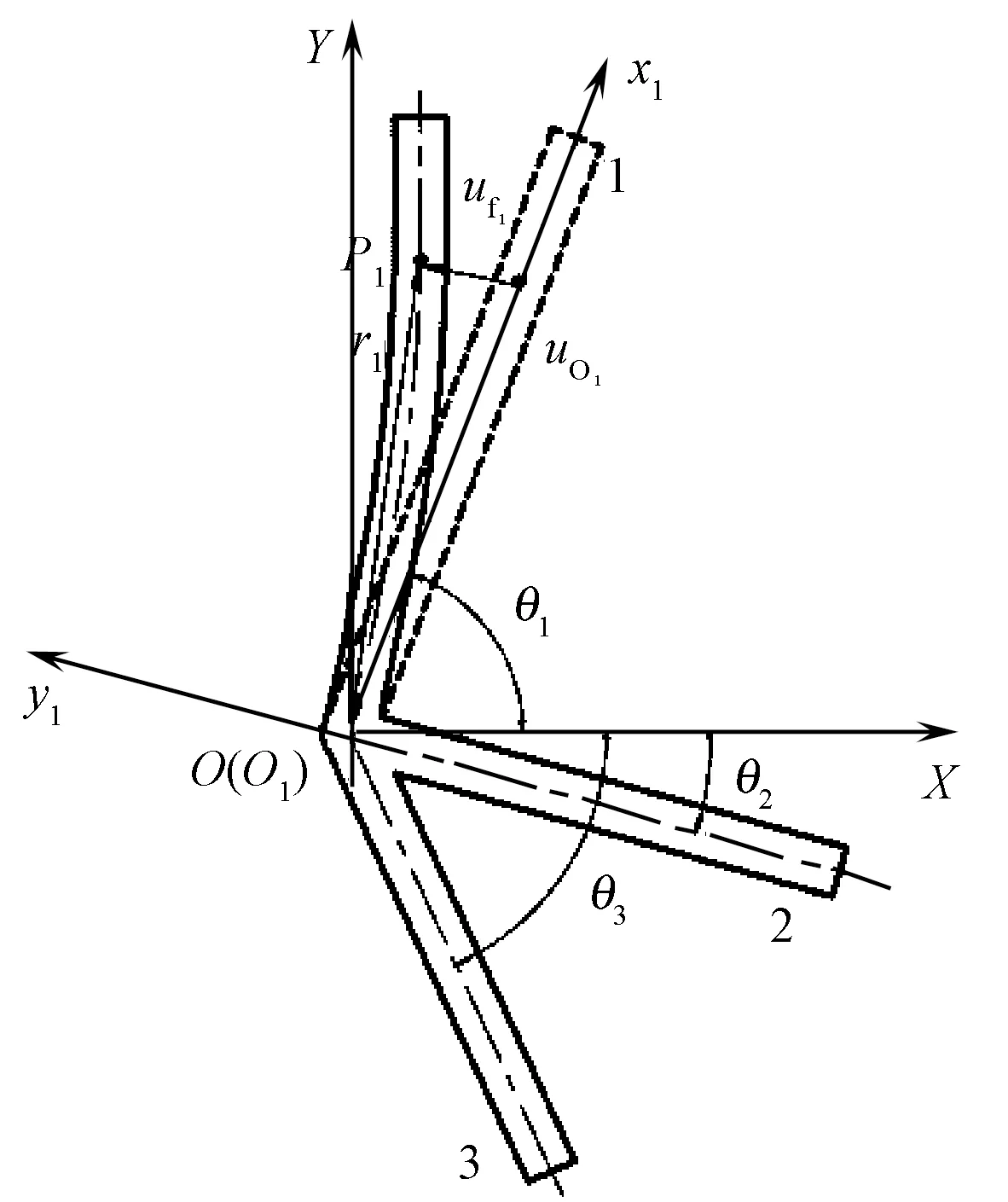
图2 共轭凸轮从动件变形示意图Fig.2 Schematic diagram of deformation of conjugate cam follower

设OXY为机构的定坐标系，O1x1y1、O2x2y2和O3x3y3为固连在杆1、杆2和杆3上的动坐标系(其中杆2和杆3的动坐标系和变形未在图中表示)。杆1、杆2和杆3的质量为M1、M2和M3，各杆端部的集中质量分别为m1、m2和m3，各杆的长度分别为L1、L2和L3，三杆均采用悬臂梁模态，θ1、θ2和θ3为杆1、杆2和杆3与定坐标系X轴的夹角。设r1、r2和r3分别为杆1上点P1、杆2上点P2和杆3上的点P3在惯性系中的位置向量，则系统的动能为

T=T1+T2+T3=

(1)

式中，ρ1(x1)、ρ2(x2)和ρ3(x3)为杆1、杆2和杆3单位长度的质量。

(2)

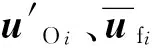
Ai为动坐标系Oxiyi到定坐标系OXY旋转变换矩阵，即

此外

式中：xi为Pi点在动坐标系Oixiyi的横坐标；vi为杆i在动坐标系Oixiyi(i=1,2,3)的横向变形。所以

且

(3)

式中δ(xi-Li)为狄拉克函数，即

θ2=θ1-α

θ3=θ1-β

式中：α为杆1与杆2之间的夹角；β为杆1与杆3之间的夹角。

将式(2)、(3)整理后代入式(1)，得到柔性从动件的动能

(4)

从动件的势能V为重力势能Vg与弹性应变能Ve之和：

V=Vg+Ve

(5)

重力势能Vg为

(6)

弹性势能Ve为

(7)

式中EiIi(i=1,2,3)为杆i抗弯截面模量。

采用Rayleigh-Ritz法对弹性变形广义坐标进行离散化处理。选取一组Ritz基函数φj(x) (j=1,2,…,n)进行离散化，将v1，v2，v3展开为

其中

λ1Li=1.875

λ2Li=4.694

λ3Li=7.855

(i=1,2,3; j=1,2,3,…,n)

取n=2，并令φ1(xi)、φ2(xi)为悬臂梁的前2阶模态，则广义坐标为

将所求得的动能和势能分别代入到Lagrange方程

(8)

由此，得到从动件的动力学方程

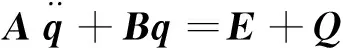
其中

式中：Akl、Bkl(k,l=1, 2, 3,…,7)均为与柔性从动件几何参数和物理参数相关的变量；Qk为广义力；E1为与重力势能相关项。

2 仿真分析

某剑杆织机共轭凸轮打纬机构，凸轮转速为400 r/min，筘座脚长为0.236 m，筘座脚密度为2 700 kg/m3，筘座脚质量为0.637 kg，弹性模量为7.6×1010N/m2，筘座脚与水平面夹角为75°；摆臂长为0.1 m，摆臂密度为7 000 kg/m3，摆臂质量为0.336 kg，弹性模量为2.09×1011N/m2；相邻各杆之间的夹角为120°，凸轮升程运动角为70°，筘座角度冲程为30°，滚子的质量均为0.5 kg，筘座质量为1 kg，推程阶段采用余弦加速度运动规律。

根据建立的柔性从动件共轭凸轮打纬机构动力学方程，用MatLab仿真得到打纬过程中仿真曲线图。图3 示出筘座位移和角加速度偏差。从图3(a)得到筘座的实际位移与理论位移存在偏差，且偏差均为正值，说明筘座出现过摆现象；从图3(b)可发现，由于打纬机构的振动使筘座的角加速度存在较大的偏差，最大偏差值达到7.8 rad/s2，这将会造成推程阶段加速度变化迅速，传递到织物上会产生很大的惯性力，加剧机构的振动，同时也会产生过大的打纬力，造成织物过紧，影响织造均匀性。

图3 筘座位移和角加速度偏差Fig.3 Displacement deflection (a) and angular acceleration deflection (b) of sley

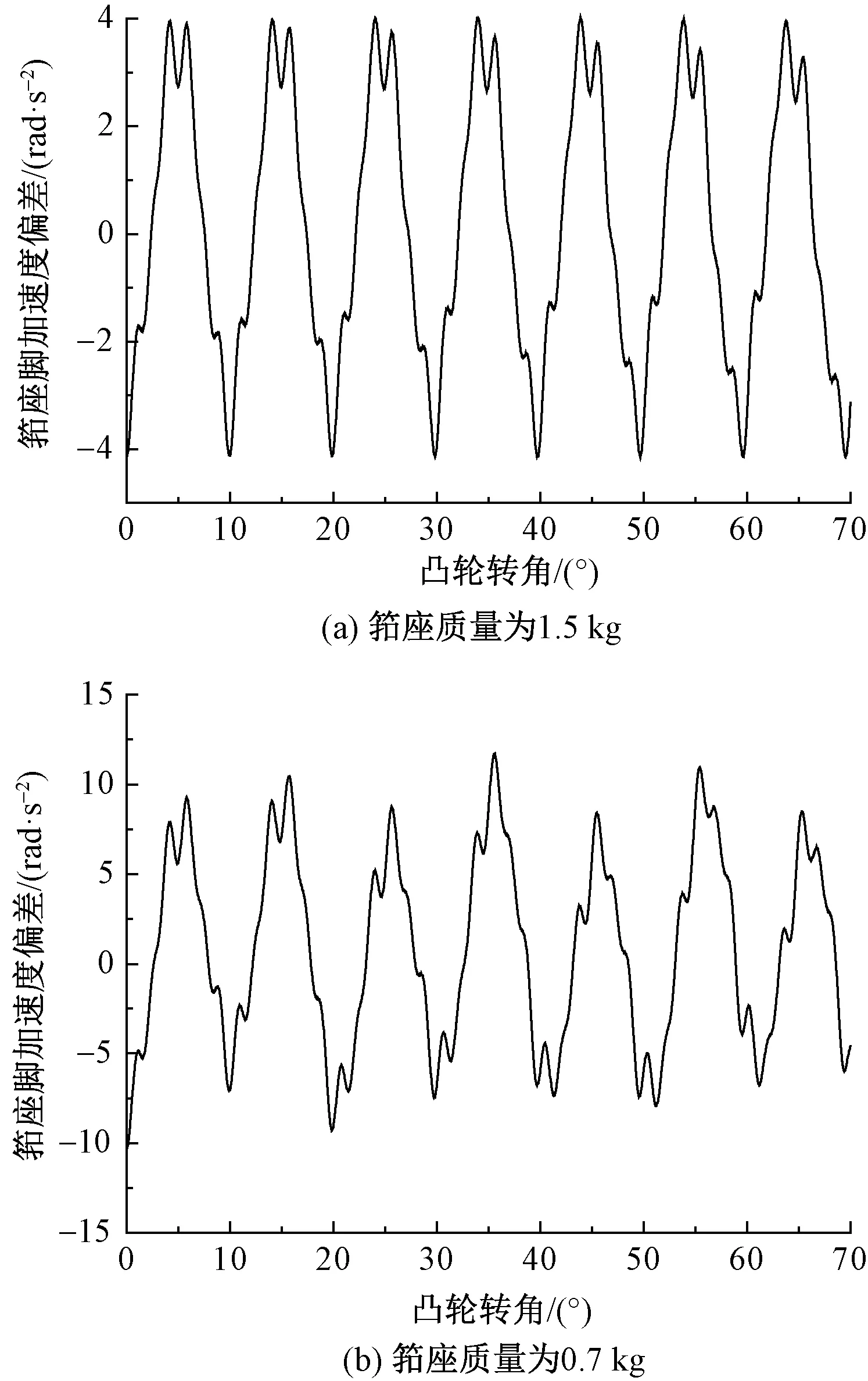
图4 不同筘座质量的角加速度偏差Fig.4 Angular acceleration deflection with different mass of sley. (a) Mass of sley 1.5 kg；(b) Mass of sley 0.7 kg

图5 不同筘座脚质量的角加速度偏差Fig.5 Angular acceleration deflections with different mass of sley feet. (a) Mass of sley feet of 1 kg；(b) Mass of sley feet of 0.3 kg

图4示出筘座质量为1.5 kg和0.7 kg的仿真图。可以看出，增加筘座质量角加速度的偏差减小，而减小筘座质量角加速度的偏差变大。图5分别为筘座脚质量为1 kg和0.3 kg的仿真图。可以看出，增加筘座脚质量角加速度的偏差增大，而减小筘座脚质量角加速度的偏差变小。可见，增大筘座质量和减小筘座脚质量都可以使筘座的角加速度偏差减小，但增加筘座质量会使从动件的惯性力增大，从而会增大滚子与凸轮的接触力，所以应该通过减小筘座脚的质量来减小筘座的角加速度偏差。

3 结 论

1) 基于Lagrange方程建立了柔性从动件共轭凸轮的动力学模型，并用Rayleigh-Ritz方法对从动件进行了离散化处理，能够更为真实地反映剑杆织机共轭凸轮打纬机构的动态特性。

2) 凸轮摆杆从动件的柔性变形及横向振动，使筘座发生过摆现象，筘座角加速度发生较大幅度的波动，会影响织造的均匀性。

3) 仿真分析表明，减小筘座脚质量可以减小筘座角加速度的偏差。

[1] 张雷，余克龙，陈少钟，等. 基于ANSYS和ADAMS空间四连杆引纬机构的柔性动力学仿真[J]. 纺织学报，2013, 34(5): 116-120. ZHANG Lei, YU Kelong, CHEN Shaozhong, et al. Flexible dynamics simulation for spatial four bar linkage weft insertion mechanism based on ANSYS and ADAMS[J]. Journal of Textile Research, 2013, 34(5): 116-120.

[2] 马骏，王俊元，杜文华，等. 糖果包装机推糖机构运动分析[J]. 包装工程, 2014, 35(21): 1-5. MA Jun, WANG Junyuan, DU Wenhua, et al. Kinematic analysis of feeding mechanism for candy packaging machine[J]. Packing Engineering, 2014, 35(21): 1-5.

[3] 吕剑，许秦蓉. 基于试验模态方法的递纸机构优化设计[J]. 包装工程, 2015, 36(5): 90-94. LÜ Jian，XU Qinrong. Design optimization of paper-feeding mechanism based on experimental modal Analysis[J]. Packing Engineering, 2015, 36(5): 90-94.

[4] 王英，陈建能，周丽莎，等. 步行插秧机共轭凸轮推秧装置动力学分析与试验[J]. 农业机械学报，2012, 43(10): 47-52. WANG Ying, CHEN Jianneng, ZHOU Lisha, et al. Dynamic analysis and experiment of conjugate cam seedling-pushing device applied on walking-type rice transplanter[J]. Journal of Agricultural Machinery, 2012, 43(10): 47-52.

[5] 唐雪梅，朱伟林，赖奇暐，等. 共轭凸轮打纬机构运动精度分析[J]. 机电工程，2014, 31(2): 173-176. TANG Xuemei, ZHU Weilin, LAI Qiwei, et al. Analysis of kinetic precision on conjugate cams beating-up mechanism[J]. Journal of Mechanical & Electrical Engineering, 2014, 31(2): 173-176.

[6] 滕兵，何勇. 共轭凸轮打纬机构弹性动力学和限元分析[J]. 机械设计与制造，2006(2): 39-40. TENG Bing, HE Yong. The analysis of conjugating cam in beating-up mechanism with finite element and elastic dynamic[J]. Machinery Design & Manufacture, 2006(2): 39-40.

[7] 苏利亚. 高速凸轮机构的动力学分析[J]. 机械设计与制造, 2008 (12): 181-182. SU Liya. Dynamic analysis of the high-speed cam gear[J]. Machinery Design & Manufacture, 2008 (12): 181-182.

[8] YAN H S, YEH C C. Integrated kinematic and dynamic designs for variable-speed plate cam mechanisms[J]. Journal of Mechanical Engineering Science, 2011, 225(1): 194-203.

[9] GIUSEPPE Carbone, CHIARA Lanni, MARCO Ceccarelli. A characterization of cam transmissions through an identification of lumped parameters[C]// ASME Proceedings of IDETC/CIE 2006.[s.l.], American Society of Mechanical Engineers, 2006: 1-10.

[10] 林万焕，王英，赵雄，等. 基于Hermite 多项式的打纬运动学方程及其应用[J]. 纺织学报，2011，32(3): 127-132. LIN Wanhuan，WANG Ying，ZHAO Xiong，et al. Establishment and application of kinematics equations of beating-up motion based on hermite polynomials[J]. Journal of Textile Research, 2011, 32(3): 127-132.

[11] MAYO J，DOMINGUEZ J. Geometrically nonlinear formulation of flexible multibody system in terms of beam elements: geometric stiffness[J]. Computer and Structures, 1996, 59: 1039-1050.

[12] 阮晓光，蔡安江. 高速凸轮机构输出端运动规律的确定[J].机械设计与制造，2005 (1): 61-63. RUAN Xiaoguang, CAI Anjiang. Making sure the fan-out movement rule of the hign-speed cam mecha-nism[J]. Machiney Design & Manufacture, 2005 (1): 61-63.

[13] 张春红. 高速凸轮机构的动态设计[J]. 机械工程与自动化, 2006 (2): 143-151. ZHANG Chunhong. The dynamic design of high-speed cam mechanism[J]. Mechanical Engineering and Automation, 2006 (2): 143-151.

[14] 杨明轩. 高速凸轮机构动力学模型研究[J].设计与研究，2007, 34(7): 21-24. YANG Mingxuan. The high speed cam gear dynamics model computation studies[J]. Design and Research, 2007, 34(7): 21-24.

[15] 邓威进，周香琴. 基于 Pro/E 的织机打纬系统载荷特性研究[J]. 机电工程，2014, 31(3): 320-324. DENG Weijin, ZHOU Xiangqin. Beating-up mechanism in rapier loom based on Pro / E loading character-istic[J]. Journal of Mechanical & Electrical Engineering, 2014, 31(3): 320-324.

Dynamic analysis of flexible follower conjugate cam beating-up mechanism in rapier loom

JIN Guoguang, QIN Kaixuan, WEI Zhan, YUAN Ruwang, ZHOU Guoqing

(AdvancedMechatronicsEquipmentTechnologyTianjinAreaLaboratory,TianjinPolytechnicUniversity,Tianjin300387,China)

The vibration of the rapier loom conjugate cam beating-up mechanism results in the sley angular acceleration deviation, reduces the weaving quality, and shortens the life of the conjugate cam. To solve these problems, conjugate cam beating-up mechanism is reasonably simplified. Flexible follower is discretized by Rayleigh-Ritz method and the dynamic equation of flexible follower is established based on the Lagrange equations. The dynamic simulation for the beating-up mechanism with flexible follower conjugate cams is carried out by MatLab. In the process of simulation, the method of reducing the vibration of beating up mechanism is explored by changing the structure parameters of the beating-up mechanism. The simulation results show that the angular acceleration of the sley will fluctuate significantly due to the transverse vibration. A method for reducing the angular acceleration deflection and reducing vibration of mechanism is proposed by reducing the mass of the sley feet.

rapier loom; beating-up mechanism； flexible follower; Lagrange equation； angular acceleration； dynamic

10.13475/j.fzxb.20150401206

2015-04-10

2016-02-02

国家自然科学基金资助项目(51475330)

金国光(1963—)，男，教授。研究方向为机器人机构学、机械系统动力学及其控制。E-mail：jinguoguang@tjpu.edu.cn。

TH 112; R 103.337.3

A