发现“隐藏直角” 提高解题效率

☉江苏省海安县胡集初级中学　卢　旭



发现“隐藏直角”提高解题效率

☉江苏省海安县胡集初级中学卢旭

直角是一类非常特殊的角，在一些中考试题中由于直角的存在便使题目具有了丰富的内涵和外延；在整个初中阶段和直角有关的知识也比较多，比如勾股定理、锐角三角函数等，对于直角三角形而言全等和相似更是有不同于一般三角形的判定方法.然而，在有些题目中，直角却不是明显存在的，需要我们“擦亮眼睛”，利用所学的知识“去伪存真”后才能够露出直角的真面目，下面以某市中考试题中的三道试题（第9、20、24题）为例，进行简单介绍，权当抛砖引玉，欢迎同行和专家批评指正.

一、圆中的直角

1.直径+所对圆周角

例1（第9题）如图1，⊙O是△ABC的外接圆，∠B= 60°，⊙O的半径为4，则AC的长等于（）.

图1

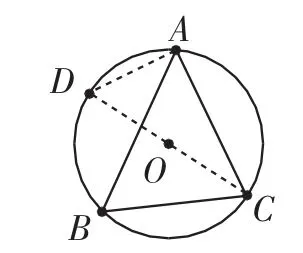
图2

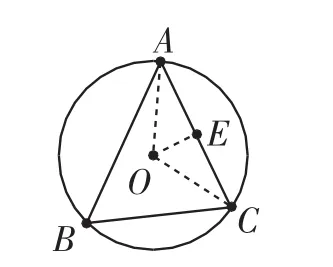
图3

解法1：如图2，连接CO，并延长交⊙O于点D，连接AD，则∠CAD=90°.

由于∠B=60°，根据圆周角的性质可得∠D=60°.

解法2：如图3，连接AO、CO，过点O作OE垂直于AC，垂足为E.

根据圆周角和圆心角的关系，可得∠AOC=120°.

又由于AO=CO，所以∠EOC=60°.

思考：解法1和解法2可以说都是非常自然、非常常规的解法.解法1主要运用了直径所对的圆周角是直角，以及圆周角的性质；解法2主要运用了圆周角和圆心角的关系，以及垂径定理.两种解法比较可以发现解法1比较简洁，符合数学在解决问题过程中“求简”的追求，笔者认为这得益于发现了图中“隐藏的直角”.