预设探究活动，促进自主学习——以圆的起始课教学设计为例

☉江苏省苏州市高新区实验初级中学　练兆明



预设探究活动，促进自主学习
——以圆的起始课教学设计为例

☉江苏省苏州市高新区实验初级中学练兆明

一、写在前面

近读初中数学专业期刊（如《中学数学》（初中版）、人大复印资料《初中数学教与学》2016年第5期等），有很多对单元起始课的课例研究，笔者受益其中，对单元起始课也有了更多的思考.近期有机会执教一节“圆（第1课时）”教研课，精心构思了教学设计，取得了较好的教学效果.本文梳理该课的教学流程，并跟进阐释教学立意，供研讨.

二、圆的起始课教学流程

（一）情境导入

（PPT）展示两幅圆形校徽，预设讲解词：圆是生活中常见的几何图形，圆形物体在生活中随处可见.圆具有独特的对称性，因此常被用来设计精美的图案.比如屏幕上呈现的是两所名校的校徽（图1，图2），都被设计成圆形图案.小学里，我们就已经认识了圆，本章，我们将系统研究圆的概念、性质，点和圆、直线和圆的位置关系，正多边形和圆的位置关系和数量关系，以及弧长和扇形的面积等计算问题.本课，我们一起来学习圆的定义及相关概念.

图1

图2

设计意图：欣赏名校校徽，感知圆的对称美，激发自己积极上进努力考上名校的斗志.

（二）理解圆的定义

（1）安排学生画圆后提问：画一个圆必须具备两个要素，即圆心和半径.

在此基础上，教师通过几何画板的动画功能再次演示画圆过程，引导学生归纳圆的定义.

定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫作圆.

预设讲评：类比三角形和平行四边形的表示方法，我们把以点O为圆心的圆，记作⊙O，读作“圆O”.

（2）观察圆的变化，我们发现，半径确定了圆的大小，圆心确定了圆的位置.

（3）例题讲评.

例1如图3，在圆O上有两点A、B，连接AB，若AC=BD，试判断OC与OD的大小关系.

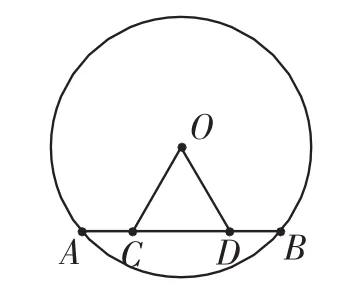
图3

预设思路1：连接OA、OB，构造全等三角形.

预设讲评：这种辅助线应用了圆的性质，今后要形成“作半径”的辅助线意识.

预设思路2：连接OA、OB，作OE⊥AB，利用等腰三角形的三线合一、线段的垂直平分线的判定证明.

（4）从集合角度定义圆.

教学预设：引导学生回顾线段的垂直平分线的定义：经过线段的中点并且垂直于线段的直线.记得线段的垂直平分线还有一个定义：它是符合一定要求的点的集合，是和线段两个端点距离相等的所有点的集合.类似地，圆可以看成到定点的距离等于定长的所有点的集合.

（5）利用定义，初识“四点共圆”问题.

例2如图4，矩形ABCD的对角线AC、BD交于点O，求证：A、B、C、D四个点在以点O为圆心的同一个圆上.

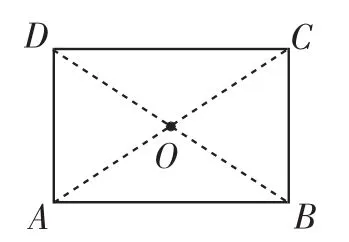
图4

教学预设：通过解决问题，巩固了圆上各点到圆心的距离都等于半径这条性质，形成了“作半径”的解题思维，为下面这道变式习题形成铺垫.

例2的变式如图5，在四边形ABCD中，∠ABC= ∠ADC=90°.

求证：A、B、C、D四个点在同一个圆上.

图5

预设思路：连接AC，取AC的中点O，连接OB、OD，借助“直角三角形斜边上的中线等于斜边的一半”证明.

预设互动：追问学生怎么想到辅助线的，及任意四个点是否都在同一个圆上，并提出一个有挑战的问题“对角互补的四边形的四个顶点在同一个圆上吗”，供学生课后深入思考.

（三）理解圆的相关概念

1.从生活图片中抽象出圆及相关概念

PPT呈现的是一扇圆形的木门（图6），抽象为几何图形（图7）.

图6

图7

教学预设：图中有熟悉的圆心、直径，还有一些线段，还有一些被圆上的点分成的若干部分，这些都是与圆有关的量，请阅读课本，在图7中找出与圆有关的概念.

2.学生展示自学成果

教学预设：学生走上讲台，在PPT上指出图7中的弦（直径）、弧（半圆、优弧、劣弧）、等圆、等弧.

预设追问：直径是否是最长的弦？为什么？

3.巩固圆的相关概念

例3如图8，⊙O中，点D是半圆AB的中点，点C是另一半圆AB上任意一点.连接OD、CD.请分析半径、直径、弦、弧等概念.

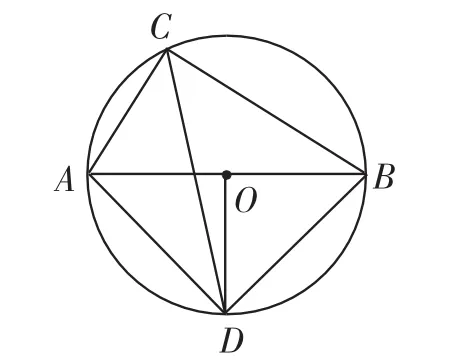
图8

教学预设：这道练习题不仅巩固与圆有关的概念，还为后续作业提供一个图形的基础（见“小结与作业”）.

（四）小结与作业

（1）本课所学的圆的相关概念，与小学中有什么不同？

（2）如图8，⊙O的直径AB为10cm，弦AC为6cm，D为弧AB的中点.你能求出图中所有线段的长度吗？你能求出哪些角的度数？你能求出哪些弧的长度？

三、教学立意的进一步阐释

1.辨识学段特征，初中圆的学习重在推理

我们发现，《义务教育数学课程标准（2011年版）》将课程内容分三个学段作出具体的要求，前两个学段属于小学阶段，第三个学段是初中阶段，细读“课标（2011年版）”文本，大家都应该能体会出不同学段对学生熟悉的生活现象或数学知识的要求是不一样的.对于初中阶段圆的学习，重点应该落在推理，即《几何原本》上倡导的推理教学.这也是上文教学设计中，我们在很多教学环节加强推理教学的原因，比如直径为什么是圆中最长的弦，矩形的四个顶点为什么能在同一个圆上，等等.这些教学环节或追问的背后，都需要备课者基于“理解数学”（章建跃博士语）的高度精心预设.

2.重视几何套路，促进自主探究圆的概念

圆是初三学习内容，之前初一、初二学生对几何图形的学习已经有了一些基本套路，比如一般都是先学习图形的定义、相关概念，然后研究这种图形的性质和判定.圆的学习也不例外，需要先定义圆，而且可以类比线段垂直平分线或角的不同定义方法，从静态、动态的角度分别定义圆，加深学生对定义的理解.再比如，在圆的相关概念（弦、弧、直径等）的教学时，我们安排学生先自学，再从生活图形中分离出圆，并辨识有哪些与圆相关的概念，这种让学生带着任务自学的活动，收到了较好的教学效果：教师没有介绍相关概念，但学生边阅读教材边对照教师给出的问题，内化了概念，学习自主性也得到了锻炼.

参考文献：

1.刘东升.辨别学段特征：初中几何教学的用力点——以“圆（第1课时）”教学为例［J］.中学数学教学参考（中），2015（3）.

2.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

3.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.Z