间接测量中不确定度计算——乒乓球转动惯量

曹先胜，吉高峰

(常州大学，江苏 常州　213164)



*通讯联系人

间接测量中不确定度计算
——乒乓球转动惯量

曹先胜*，吉高峰

(常州大学，江苏 常州213164)

摘 要：通过测量乒乓球转动惯量，介绍了间接测量中的不确定度传递和计算。研究发现乒乓球的质量是影响其转动惯量的主要因素，而内、外直径则是影响较小因素。

关键词：转动惯量；不确定度；间接测量

众所周知，在科学测量中误差总是存在的、是不可避免的、是不能消除的。唯一能做到的是尽量减小误差，提高测量可靠度。尽管目前已有许多文献和教科书都详细介绍了物理测量中的不确定度[1-5]，但利用相对简单、廉价的试验来直观介绍不确定度中的一些基本概念仍然是有必要的。本文通过测量乒乓球的转动惯量来实现上述目的。近来Pauchard和Rica研究了乒乓球形变特性[6]。Paulo和Gutemberg研究了乒乓球的厚度和密度[7]。但对乒乓球的转动惯量的研究还是比较少的。而转动惯量是乒乓球非常重要的一个物理量。

为此，本文首先介绍测量值和其不确定度的表达方式，重点介绍间接测量物理量的不确定度的传递关系。为计算各测量物理量间的变化关系，本文采用Paulo等人的方法[7]讨论了变异系数，此方法广泛应用于金融市场分析中[8]。

1理论

1.1球体

一般球的体积为：

(1)

其中d球体的直径.

于是，若乒乓球被灌满水时，乒乓球的内直径RI:

(2)

其中：Vw是灌满乒乓球的水的体积。

直径为R的球体绕z-轴转动(通过球心)时的转动惯量(I)

(3)

其中ρ球体的质量密度.

于是，球壳(乒乓球)的转动惯量(IS):

(4)

其中:RE、RI为球壳(乒乓球)的外、内直径,m为球壳(乒乓球)的质量。

1.2不确定度

不确定度不仅能用来描述的测量的可靠性，还能反映测量的精度。当人们执行测量任务时，首先需要根据要求的不确定度来制定测量计划，并根据测量此计划选择合适的仪器和实验环境。不确定度是由两部分组成：系统不确定度和随机不确定度。随机不确定度可通过统计的方法予以消除，而系统不确定度是难以评估或检测，但可通过仪器校准来减小系统误差 (本实验主要指的是游标卡尺和物理分析天平)。

在本实验中系统不确定度仅由仪器的不确定度所组成，而随机不确定度由多次、随机测量不确定度(测量置信度为95%，且满足学生t分布)所组成。

(5)

其中:N为测量次数.从公式5不难发现要想提高精度20倍，需增加测量次数400倍。而且系统误差并不能通过增加测量次数而减小，所以最好提高精度的办法是提高每次测量的精度。

当测量次数接近无穷时，测量的物理量的概率密度遵从正态分布。当减少测量次数时，概率密度变扁平，呈t-分布，又称学生分布；当测量次数趋于无穷时，t-分布又再一次变成正态分布。t-分布常被用来计算测量次数较少(如10次，小于30次)时的不确定度，在可信度95%时，随机不确定度为标准差的2.262倍[9]。于是最终的不确定度δx为 (6):

(6)

试验中，有许多物理量不能直接通过测量获得，而需经过测量其它物理量而间接获得。于是，当一个物理量涉及间接测量时，其不确定度计算分为两步：第一步是确定直接测量的物理的不确定度，第二步是确定上述直接不确定度时怎样进行‘传递’的，换句话说就寻找它们之间的函数关系式，从而计算出最终的不确定度。

不确定度δx与相对不确定度之间的关系如下：

相对不确定度=δx/|x|

(7)

其中|x|是x的期望值，相对不确定度是无量纲量。

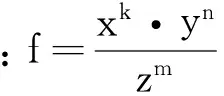
(8)

通过简单的计算可得不确定度δf:

(9)

变异系数CV(%))是衡量实验中各测量量数值变异程度的一个统计量[4]，它的定义为标准偏差与平均值的比值：

(10)

变异系数可以消除单位和(或)平均数不同对两个或多个资料变异程度比较的影响。

2实验材料与方法

5个同一厂家同一型号的乒乓球，并且分别用数字1-5在球上进行标示。第一步：用精度为0.005cm的游标卡尺对每个乒乓球外直径进行10次的测量，且每次测量时位置不同，于是得到50个测量值。第二步：用精度为5mg的分析天平对每个乒乓球进行10次测量；第三步：利用注射器给每个乒乓球注满水。由于注射器的针头直径较小，所以对乒乓球形状影响较小可忽略。第四步：利用上述同一分析天平进行对每个注满水的乒乓球进行10次测量。于是，得到以下测量量：乒乓球的外直径(RE)、空乒乓球的质量(ME)、注满水的乒乓球的质量(Mw)。通过一些简单计算还可得到以下物理量：乒乓球注满水时的水的体积(即乒乓球内体积)(Vw)、乒乓球的内直径(RI)。最后，利用公式4，计算出乒乓球的转动惯量。

3实验结果

见表。

注：倒数第3行中括号里的数字表示的是不确定度，例如3.975(5)cm表示的是 (3.975 ± 0.005)cm

注：括号里的不确定度根据方程5计算，乒乓球内体积即水的体积

注：内直径根据公式(3)计算出来

注：乒乓球的转动惯量的不确定度(δIS)通过它的平均值(|IS|) 乘以空乒乓球质量的相对不确定度(δm/|m|)与其内、外直径的相对不度额定度之和(δR/|R|)(如公式9)

4讨论

分析表1-5，不难发现测量数据(乒乓球的质量、外直径、充满水时的质量)与文献5的结果相似。这是由于实验所使用的乒乓球是一星级的常用乒乓球，其质量在2.35到2.63g之间，圆度误差小于0.25mm，硬度小于1.10mm。这类乒乓球常用于学校、军队等其它业余比赛活动。换句话说，实验中用的乒乓球是最常用普通乒乓球，在普通市场均买到。

所以不难得到以下结论：空乒乓球的质量是影响其转动惯量的主要因素，而内、外直径则是次要因素。这主要是由内外直径间相差较小所致。

乒乓球2的外直径的变异系数最大，球4和5最小(表1)；空乒乓球4和5质量的变异系数相等，球1-3的变异系数也相等，但前者小于后者。注满水时乒乓球质量的变异系数均相等。所以球4和5的数据测量较为集中，离散度较小。

5结论

本文介绍了物理实验中的不确定度的一些基本概念(如不度额定度传递性)并通过测量乒乓球的转动惯量来验证。验证发现空乒乓球的质量是影响对其转动惯量的主要因素，而内、外直径却是次要因素。并利用变异系数来评估测量的实际变化。

参考文献：

[1]TaylorJ.R.AnIntroductiontoErrorAnalysis[M].theStudyofUncertaintiesinPhysicalMeasurements2ndedn,1997,(Sausalito,CA:UniversityScienceBooks)

[2]BraddickH.J.J.ThePhysicsofExperimentalMethod[M].1956,(London:ChapmanandHall).

[3]GrabeM.MeasurementUncertaintiesinScienceandTechnology[M].2005,(NewYork:Springer).

[4]娄航宇，王威，孙维民.三线摆测量转动惯量方法的改进及确定度分析[J].大学物理实验，2015(6)：102-105.

[5]胡勇，王严东.浅议物理实验测量误差和不确定度的异同[J].大学物理实验，2015(1)：93-95.

[6]PauchartLandRicaS.Contactandcompressionofelasticsphericalshells:thephysicsofa‘ping-pong’ball[J].1998,Phil.Mag.78 225-233.

[7]PauloAdeSouzaJrandGutembergHespanhaBrasil,Assessinguncertaintiesinasimpleandcheapexperiment[J].Eur.J.Phys,2009,30 615-622.

[8]PangKW,Wing-TongY.B.MarvinTandHouS.H.Asimulation-basedapproachtothestudyofcoefficientofvariationofdividendyields[J].Eur.J.Oper.Res.2008,189,559-569.

[9]OttR.L.andLongneckerM.AnIntroductiontoStatisticalMethodsandDataAnalysis5thedn[M].2001(PacificGrove,CA:Duxbury).

AssessingUncertaintyofIndirectMeasurementinaSimpleExperiment

CAOXian-sheng

(ChangzhouUniversity,JiangsuChangzhou213164)

Keywords：rotationalinertia；uncertainty；indirectmeasurement

Abstract：Itdescribeshowtocalculatemeasurementuncertaintiesusingasapracticalexampletheassessmentoftherotationalinertiaofthesphericalshelloftheping-pongballs.Themassesoftheemptyping-pongballsaretheinfluenceoftherotationalinertiaoftheping-pongballmajorfactor,internalandexternaldiameterlessinfluencefactors.

收稿日期：2016-01-31

文章编号：1007-2934(2016)03-0122-04

中图分类号：O4-34

文献标志码：A

DOI：10.14139/j.cnki.cn22-1228.2016.003.032