电阻丝电阻率的测量及测量结果的评定
郭 琦
(南京师范大学,江苏 南京 210042)
电阻丝电阻率的测量及测量结果的评定
郭琦
(南京师范大学,江苏 南京210042)
摘 要:采用惠斯通电桥测量了电阻丝的电阻率,对各不确定度分量及自由度进行了评定,描述了电桥灵敏度引入的测量不确定度评定方法,给出了电阻丝电阻率的测量值及不确定度评定结果。
关键词:电桥;电阻率;不确定度
电阻率是材料的一个重要电磁参量,通常采用开尔文双臂电桥测量电阻,再计算出电阻率[1-3]。在大学物理实验中,采用惠斯通电桥测量了电阻丝等电阻率较大材料的电阻率,不仅让学生掌握电桥的工作原理和具体测量过程,同时与长度、直径等物理量测量联系起来,由电阻的测量推广应用到电阻率的测量,提升了学生综合实验能力[4-7]。大学物理实验需要编写实验报告,对实验结果进行评定,测量结果可信程度要用测量不确定度来评定,而不确定度的可信度用自由度来评定[8-9]。本文主要阐述电阻丝电阻率的测量过程及结果、电阻率测量不确定度的影响因素及其评定方法,期望该方法对大学物理教学及学生实验工作有所帮助。
1电阻丝电阻率的测量
1.1电阻及电阻率的测量
测量电阻丝的电阻率需要先测量电阻丝的电阻,电阻丝电阻采用惠斯通电桥测量,惠斯通电桥测电阻的工作原理见图1所示。
图1中,AB、AD、BC、DC为电桥的四个臂,其中AB、AD、BC三个臂接三个已知电阻,DC接被测电阻丝电阻Rx。对角A和C之间加上电源E、滑动变阻器RE、开关KE,对角B和D之间连接检流计G、开关KG、滑动变阻器RG。当调节R1、R2、R0到一定数值时,B、D两点的电位相等,检流计中无电流通过,电桥就达到了平衡。当电桥平衡时,待测电阻丝电阻Rx大小用(1)式计算。
(1)
对于横截面一定、材料均匀的电阻丝而言,其电阻率的计算公式用(2)式表示。
(2)
式中:ρ为电阻丝电阻率,Ω·m;S为电阻丝横截面积,m2;L为电阻丝长度,m。电阻丝直径用d表示,(2)式可变成(3)式。
(3)
选用电阻率较高的铝镍铁合金作为待测对象,用螺旋测微器测量电阻丝直径,用米尺测量电阻丝长度,选择合适的三个标准电阻箱,按照图1所示连接电路,测量电阻丝电阻。电阻丝直径、电阻丝长度、电阻丝电阻分别测量了六次,测量结果用算数平均值表示,实验标准偏差用贝塞尓公式(4)式计算。
(4)
电阻丝直径、电阻丝长度、电阻丝电阻各自测量的平均值及实验标准偏差见表1所示。
根据表1的数据,应用公式(3)计算出电阻丝电阻率为1.67×10-6Ω·m。
1.2电桥灵敏度的测量
公式(1)是在电桥平衡的条件下推导出来的,判断电桥平衡的条件就是观察检流计有无偏转。理想条件下,电桥平衡时通过检流计的电流为零,但检流计的灵敏度总是有限的,当检流计的偏转小到感觉不到时(如小于0.1格),可认为电桥平衡了,所以待测电阻Rx的测量结果应考虑电桥灵敏度对测量结果的影响。为方便分析检流计的灵敏度引起的测量不确定度,引入了电桥灵敏度的概念,电桥灵敏度S用(5)式表示。
(5)
式中:△n是由于电桥偏离平衡而引起检流计的偏离格数;△Rx是在电桥平衡后Rx的微小改变量。S的单位为格,它表示电阻Rx改变百分之几可使检流计指针偏转1格。S值越大,说明电桥的灵敏度越高。由于待测电阻是恒定量,不能用改变Rx的方式测量灵敏度S,但可以通过改变R0的方式来测量灵敏度S,(5)式可以用(6)式表示。
(6)
式中:△R0是在电桥平衡后R0的微小改变量。
与测量待测电阻Rx的方法相同,电桥达到平衡之后,调节标准电阻R0的大小,为了便于观察,减小测量不确定度,使检流计读数偏移10格,同时记录电桥平衡时的标准电阻值及电桥偏移后标准电阻值的变化量,用(6)式计算灵敏度S的值,重复测量6次,得到灵敏度的平均值为3.15×103,实验标准偏差为2.0×102。
2测量不确定度的评定
由电阻率的测量公式(3)可以看出,待测电阻丝电阻率ρ的测量不确定度主要由电阻丝长度L测量、电阻丝直径d测量、电阻丝电阻Rx测量引入的不确定度分量三部分组成。在电阻测量过程中由于电桥不可能完全平衡,检流计中有微弱电流通过,应考虑电桥灵敏度S引入的不确定度分量;此外,测量环境温度、接触电阻等因素对测量结果都有影响,但文章暂且不予考虑。
2.1各不确定度分量的评定
2.1.1电阻丝直径d引入的测量标准不确定度分量
测量电阻丝直径的分散性不会超过最小分度的1/2,所用螺旋测微器读数的最小分度为0.01mm,最小分度的一半就为0.005mm,按均匀分布考虑,直径d测量仪器读数偏差引入的不确定度 用(7)式计算。
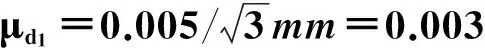
(7)
测量直径d的螺旋测微器经检定合格,测量不确定度按0.003mm计算时,不确定度分量μd1的自由度vd1为∞。
根据表1可知,电阻丝直径测量的实验偏差为0.008mm。以算术平均值作为测量结果时,重复性测量引入的不确定度用(8)式计算。
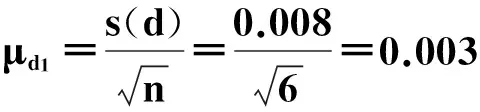
(8)
计算得出电阻丝直径d测量重复性引入的不确定度分量为0.003mm。表1中,电阻丝直径测量次数是6次,所以测量重复性引入的测量不确定度的自由度 为6减1,等于5。
根据方和根法用公式(9)计算得到电阻丝直径d的测量合成标准不确定度。
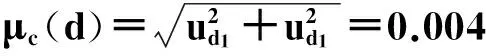
(9)
电阻丝直径d测量的合成标准不确定度的有效自由度用v1表示,用(10)式计算,计算结果舍去小数部分取整数。
(10)
由(3)式可知,电阻丝直径d的灵敏系数 用(11)式计算。
(11)
电阻丝直径d引入的不确定度分量μ1用(12)式计算
μ1=|cd|μc(d)=1.1×10-2×0.004×10-3=4.4×10-8Ω·m
(12)
2.1.2电阻丝长度L引入的测量标准不确定度分量
电阻丝长度L引入的测量标准不确定度与2.1.1节评定方法相同,长度测量所用米尺的最小分度为1mm,最小分度的一半为0.5mm,长度L测量读数偏差引入的不确定度 值为0.3mm,不确定度分量μL1的自由度vL1为∞。利用表1数据计算得到重复性引入的不确定度分量 为0.8mm,测量重复性引入的测量不确定度的自由度 等于5。计算得到电阻丝长度L的测量合成标准不确定度μc(L)等于0.9mm,有效自由度 等于8。
由(3)式可知,电阻丝长度L的灵敏系数 用(13)式计算。
(13)
计算得到电阻丝长度L引入的不确定度分量μ2等于1.5×10-9Ω·m。
2.1.3电阻丝电阻Rx引入的测量标准不确定度分量
电阻丝的电阻Rx是用惠斯通电桥测量得到,根据公式(1)可得电阻Rx的测量不确定度主要由电阻R1、电阻R2及电阻R0测量不确定度分量的合成得到,经评定得到这三个分量的合成标准不确定度 等于0.3Ω,自由度 等于50,为了突出重点和考虑文章篇幅,这里只给出评定结果。
另外,在电阻测量过程中,电桥实际上不是完全平衡的,从而引入电桥灵敏度测量不确定度分量,相关文献这方面的论述较少,因而以下内容较详细论述了灵敏度测量引入的不确定度及自由度评定过程。
把(5)式变换成(14)式
(14)
(14)式中,△n取最小可分辨数1格,灵敏度S的测量值为3.15×103格,从表1可知,Rx的测量均值 为20.5Ω,(14)式可以写成(15)式。
(15)
计算得到△Rx的值为0.007Ω,按均匀分布计算电桥灵敏度S引入的不确定度分量 为0.004Ω。
从(15)式得到△Rx的相对合成标准不确定度用(16)表示。
(16)
(17)
利用表1数据计算得到电阻测量重复性引入的不确定度分量μRx3为0.12Ω,测量重复性引入的测量不确定度的自由度vRx3等于5。计算得到电阻丝电阻Rx测量合成标准不确定度μc(Rx)等于0.32Ω,有效自由度用v3等于51。
由(3)式可知,电阻丝电阻Rx的灵敏系数 用(18)式计算。
(18)
计算得到电阻丝电阻Rx测量引入的标准不确定度分量 等于2.6×10-8Ω·m。
2.2合成标准不确定度μc(ρ)
电阻丝直径d、长度L与电阻Rx测量引入的不确定度分量是相互独立的,所以电阻丝电阻率ρ的合成标准不确定度用(19)式计算。
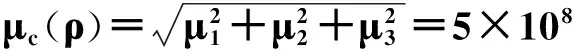
(19)
电阻丝电阻率ρ的合成标准不确定度的有效自由度veff用公式(20)计算。
(20)
2.3测量结果
铝镍铁电阻丝电阻率测量值为1.67×10-6Ω·m,合成标准不确定度为5×10-8Ω·m,有效自由度为24,测量结果用(21)式表示。
ρ=1.67×10-6Ω·mμc(ρ)=5×10-8Ω·m,veff=24
(21)
3结束语
大学物理实验教学工作中,可采用惠斯通电桥测量铝镍铁电阻率较大电阻丝的电阻率,不仅让学生掌握电桥的工作原理和具体测量过程,同时学会与长度、直径等物理量建立联系。电阻率测量不确定度分量主要包括电阻丝直径、长度及电阻测量引入的不确定度,在电阻不确定度分量评定时,考虑了电桥灵敏度引入的不确定度,建立了灵敏度与被测电阻之间的函数关系,对电桥灵敏度引入的测量不确定度分量及自由度进行了较详细的评定,给出了电阻率测量结果,期望该方法对大学物理教学及学生实验工作有所帮助。
参考文献:
[1]阿不都拉·阿吉,木扎帕尔·阿迪力,杨占全.开尔文电桥测电阻及用VisualBasic处理测量数据[J].大学物理实验,2013,26(2):71-72.
[2]郑庆华,童悦.双臂电桥测低电阻[J].物理与工程,2009,19(1):36-38.
[3]盛妍.双臂电桥测低电阻实验中的电路故障分析和排除[J].大学物理实验,2010,23(5):35-37.
[4]龙涛,等.大学物理实验[M].北京:清华大学出版社,2012.
[5]沈元华.设计性研究性物理实验教程[M].上海:复旦大学出版社,2004.
[6]谭兴文,韩力.惠斯通电桥灵敏度的探究[J].西南师范大学学报:自然科学版,2008,33(4):149-152.
[7]陈毓斌.惠斯通电桥测电阻的误差分析[J].技术物理教学,2004,12(1):32-33.
[8]全国法制计量技术委员会.JJF1059.1-2012,测量不确定度评定与表示[S].北京:中国质检出版社,2013.
[9]李金海.误差理论与测量不确定度评定[M].北京:清华大学出版社,2012.
MeasurementofResistivityofElectricResistanceWireandEvaluationofUncertaintyinMeasurementResult
GUOQi
(NanjingNormalUniversity,JiangsuNanjing210042)
Keywords:electricalbridge;resistivityofelectricresistance;uncertaintyevaluation
Abstract:TheelectricalresistivityofresistancewirewasmeasuredbyWheastonebrigemethod.Thecomponentofuncertaintyanddegreeoffreedomwereevaluated.Themeasurementuncertaintymethodofthebridgesensitivitywasintroduced.Themeasurementresultandcombinedstandarduncertaintyofelectricalresistivitywereassessed.
收稿日期:2016-02-03
文章编号:1007-2934(2016)03-0118-04
中图分类号:O4-34
文献标志码:A
DOI:10.14139/j.cnki.cn22-1228.2016.003.031

