用Mathematica计算油滴电荷的基本量

方淑婷，鲁晓东

(东海科学技术学院，浙江 舟山　316000)



*通讯联系人

用Mathematica计算油滴电荷的基本量

方淑婷，鲁晓东*

(东海科学技术学院，浙江 舟山316000)

摘 要：密立根油滴实验的主要目的是要从大量的实验数据中证明电荷的不连续性，为提高计算效率，本文利用了Mathematica软件对实验数据进行了最小二乘处理，优化了误差的分布，得到了准确的电荷基本量值。

关键词：密立根油滴;电荷量;基本带电量;Mathematica;数据处理

密立根油滴实验，是物理学史上的经典实验。该实验精确地测定了基本电荷的数值[1]，证明了所有电荷都是基本电荷的整数倍，明确了电荷的不连续性。但在实际的实验教学过程中，往往把该公认值当作已知值代入结果表达式,仅对实验数据进行了验证，虽然节省了实验时间，但不符合物理实验数据处理的一般规则，因为事先“电荷的不连续性”及“基本电荷量公认值”是未知的，而这两点正是本实验需要验证的内容。较科学的方法应该是：使用大量的实验数据表达出数据的分布规律，然后用最大公约数法[2]、多次逐差法[3]，统计法[4]等对数据进行处理，找出表征电荷不连续的特征值；如果用手工计算或借助计算机高级语言C，Baisc进行编程处理[5]，这对于低年级的学生是有困难的，影响教学效果。所以在此提出使用Mathematica软件，该软件的特点是表达上贴近于原始的数学表达，有利于不懂计算机语言的人使用，另外该软件还提供了大量的数据计算的工具包，包括优化，作图等，适合对实验数据的处理和可视化表达。

1油滴电荷测量原理：

密立根油滴实验通过控制静电场中带电油滴在空气中的运动，检测相应的参量并计算得到油滴的带电量。不妨设一个质量为m、带电量为q的油滴处在两块平行极板之间，在平行极板未加电压时，由于空气阻力的作用，加速一段距离后，油滴将作匀速运动，速度为vg，这时重力与阻力平衡(空气浮力忽略不计)，根据托克斯定律，粘滞阻力为

fr=6παηvg

(1)

式中：η为空气的粘滞系数；α为油滴的半径。通过将油滴放在平行板上加压后，油滴将处于场强为E的静电场中，并加速上升，但最终在空气阻力影响下做匀速运动即重力电场力空空气阻力三者平衡

fr=qE-mg

(2)

根据(1)(2)以及实验参数值[1]，当测出其匀速上升时的速度即可解出q：

(3)

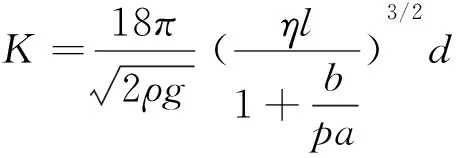
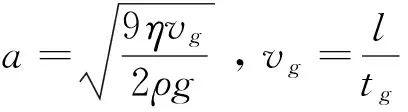
同时也可以测得同一油滴所带电荷的改变量△q(可用紫外线或放射源照射油滴，使它所带电荷改变)，得到另一组数据。但要证实电荷的不连续性，则要取多个电量值，计算它们最大公约数，得到基本电荷电量的数值，所以油滴所带电量的计算和分析是得到实验结果的关键。从上述原理中也可以看出，在实验过程中将会出现一系列影响实验结果的误差，计时的精度、电压的波动以及油滴本身的挥发等，而且其方程未知数较多使得计算量较大。

2数据处理方法分析：

2.1倒过来验证法

当我们在实验室中测得U、t后计算得出q，以基本电荷的公认值为最大公约数去除测得油滴的电荷数n，接下来便是通过e=q/n中找出这个e0，最终得出e0约为1.60×10-19c从而验证电荷的不连续[6]。这种以已知值去验证已知值的方法颠倒了过程的因果关系，所以不利于培养学生的探索精神。

2.2油滴电量平均值逐项相减法

该方法先将带相同电荷数的电量取平均，然后再逐项相减则得平均电量差Q 值，最后对在误差范围内近似相等的几个最小Q 值取平均即可获得基本电荷实验值[3]。显然,在平均值逐项相减法中体现了对随机误差抵偿性的考虑,充分利用了实验数据,从而克服了在实验数据中带相同电荷数油滴电量测量值不止一组情况下逐项相减法所必定产生的基本电荷估计值偏小的弊病，由电量逐项相减法的结果可以看出，油滴所带的电量是不连续的。从教学效果上看,它可以使学生充分利用有限的实验数据,并有效地克服实验仪器精度不高的负面影响，解决了教学中的一个难题。但在此基础上还可以在数据处理过程中继续优化，比如在计算平均值的时候，根据该电量出现不同次数加以权重，对估计值的控制时选用最小二乘的原则等，这些用手工计算是很大的工程，而借助于Mathematica软件来处理则是仅需要你的想法与步骤。

2.3基于Mathematica的方法

方法的特点就是借助软件的功能去处理一些繁琐的重复的计算。当实验测得大量的数据后，先对其进行统计分组，即按电荷量数据分成若干等间隔区域，并按间隔进行频数的统计，并且用图的方式表达。观测其分布，当存在基本电荷量时，数据是一簇一簇的，有明显的不连续分布特征，接下来便可以计算簇与簇之间的距离，这就是这些数据最大公约数的粗略估计，这时各量子数也可以确定。计算的过程中我们可采取最小二乘方法对电荷基本量估计作进一步的优化，减少误差的影响。这样的过程是符合了实验探索思路，尽管计算量很大但这些都可以借助软件来完成。以我们13级学生的数据为例，对各班近150组的实验数据进行如下的处理：(数据存放由于exdata.xlsx中)

(1)根据平衡电压和运动时间计算油滴带电量

ρ=981;g=9.793;η=1.8310-5;l=2.10-3;b=6.1710-6;p=76;d=5.10-3;(*实验条件*)

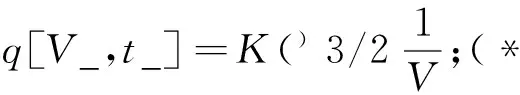
mydata=Import["E:\exdata.xlsx",{"Data",1}];(*打开excel数据文件*)

myq=Apply[q,mydata,1];(*把实验数据代入公式计算q值,存到变量myq*)

(2)根据电荷量进行统计分组

由实验数据的范围组数，以及仪器(MOD-5型)的精度和实验过程中的不确定度的估计，取间隔为0.05(×10-19c)进行统计如图所示，图1显示了各数据簇的不连续性，

TheArea=Table[0.05k,{k,0,200}];(*统计电荷量间隔的分布存到TheArea*)

Ncount=BinCounts[myq,{TheArea}];(*统计电荷量myq在各区间内的频数存到Ncount*)

listdata=Table[{TheArea[[n]],Ncount[[n]]},{n,200}];

ListPlot[listdata,Filling→Axis,PlotRange→{{0,10},{0,10}}}](*统计图形显示*)

(3)电荷基本量的估计

(4)加权最小二乘法

w=∑pi(qi-nie0)2→min

在软件中可以直接调用数值计算工具[7]minimize[]就可以了。其使用格式为：Minimize[f,{x,y,...}]，f为要优化的表达式即∑pi(qi-nie0)2，{x,y,…}为要估计的参数即e0，函数结果返回表达式的最小值。

p={0.087,0.196,0.348,0.239,0.13};(*出现的概率，见表1*)

q={1.57,3.125,4.94,6.26,8.11};(*各数据簇的期望值，见表1*)

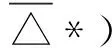
n=Round[q/del];(*电荷量的量子数*)

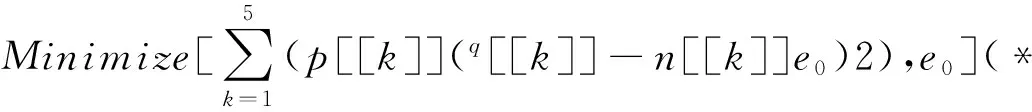
结果为{0.01,{e0→1.604}}表示电荷的基本量为1.604×10-19c，拟合的残差方和为0.01，与公认值比较百分差为0.25%。若按已知的理想值的公认值去估计本次实验的结果则为1.59,百分差为0.6%，属于同一级的精度，所以借助Mathematica计算的结果是比较理想的，并且其处理过程符合科学实验的要求[8-9]。

3结束语

密立根油滴实验是通过对宏观量的观测来揭示微观量本身所具有的属性，所以必定要通过对大量观测数据的计算和统计。用计算机软件辅助实验数据处理，不仅仅是提高计算的效率，更重要的是可以挖掘数据背后大量的信息，揭示其中的物理规律。Mathematica 正是这样的软件，它提供了大量直接可调用的数学工具包，为实验的进一步探索创造了条件。

参考文献：

[1]竺江峰,芦立娟,鲁晓东.大学物理实验[M].北京:中国科学技术出版社,2005.

[2]王广涛,陈 健,魏建宇等.密立根油滴实验数据的处理方法[J].物理实验,2004,24(12):22-24.

[3]刘才明.密立根油滴实验数据处理方法分析[J].浙江大学学报：自然科学版,1996,30(6):736-741.

[4]温猛,洪朱旭,冯运军,等.密立根油滴实验的概率统计分析[J].中山大学学报：自然科学版,2004(S1):33-35.

[5]段苹,王吉有,秦丽,等.计算机编程在密立根油滴实验中的应用[J].大学物理实验,2014,27(1):70-73.

[6]师文庆,吕楠,陈劲民.验证法处理密立根油滴实验探讨[J].广东海洋大学学报,2009,29(4):67-69.

[7]张韵华，王新茂.Mathematica 7 使用教程[M].安徽：中国科学技术大学出版社，2012.

[8]张鑫，郭胜，李钰.C语言在密立根实验数据处理中的应用[J].大学物理实验，2015(1)：63-65.

[9]林曼虹，黄烧灿，林丰，等.利用精密秤测量微小电量[J].大学物理实验，2015(1)：29-31.

Calculating the Base Charge of Oil Drop by Mathematica

FANG Shu-ting,LU Xiao-dong

(Donghai Science and Technology College,Zhejiang Zhoushan 316000)

Key words：Milliken oil drop；quantity of charge；basic charge；Mathematica；data processing

Abstract：Millikan oil drop experiment is aimed at proving the uncontinuous change carried by each oil drop.In order to improve calculation efficiency for these lots of experiment data,a method based on Mathematica is provided.By its way of MLS processing and error optimizing,the accurately value of base charge is calculated.

收稿日期：2016-02-24

基金项目：浙江省2015年度高等教育课堂教学改革项目(kg2015577)

文章编号：1007-2934(2016)03-0107-04

中图分类号：O 4-39

文献标志码：A

DOI：10.14139/j.cnki.cn22-1228.2016.003.028