基于MATLAB的载流圆环磁场分布的动态仿真

徐胜男，任学智，位浩杰，展凯云，陈文娟

(中国石油大学(华东)，山东 青岛　266580)



基于MATLAB的载流圆环磁场分布的动态仿真

徐胜男，任学智，位浩杰，展凯云，陈文娟*

(中国石油大学(华东)，山东 青岛266580)

摘 要：根据毕奥—萨伐尔定律推导出载流圆环空间磁场分布的积分表达式，利用MATLAB给出计算结果，并对磁场分布矢量图、中心轴线上磁场分布图、与圆环面平行及垂直的面上磁场分布图进行仿真，研究了磁场在径向和轴向的三维分布，对教学和实际工程应用具有一定的指导作用。

关键词：毕奥—萨伐尔定律；载流圆环；MATLAB；磁感应强度

关于载流圆环的磁场分布，在大学物理中我们了解的只是部分区域的磁场分布，而在理论和实际应用中，载流圆环全空间的磁场分布也非常重要。为了解决此问题，很多学者在毕奥—萨伐尔定律的基础上，对完整的载流圆环磁场分布进行了研究。贾瑞皋、薛庆忠在电磁学书中分析了轴线上的磁场分布情况[1]；向裕民利用椭圆积分计算失势，再经旋度求得磁场表达式，讨论了以圆环平面、中心轴线和远区场为特例的磁场分布[2]；罗宏超、朱平、王晓颖、陈丽群等人从毕奥—萨伐尔定律出发讨论了中心轴线、圆环平面、远区及圆心附近的磁场分布[3-6]；刘保义等利用mathematica4.0得到了磁感应强度分布矢量图，讨论了中心轴线和圆环平面的磁场分布[7]；王玉梅等利用MATLAB符号积分绘制圆环周围磁场分布图，并进行数值计算讨论[8]。但是，之前尚未见有人对与圆环面平行及垂直的面上磁场分布做过研究，所以，本文将着重研究磁场在圆环径向和轴向的三维分布情况。

本文根据毕奥—萨伐尔定律推导出载流圆环在空间的磁场分布的积分表达式，利用MATLAB软件编程，结合分段求和的思想，对不同情况下的磁场分布进行建模仿真，绘制了磁场分布矢量图、中心轴线上磁场分布图、与圆环面平行及垂直的面上磁场分布图，研究了磁场在圆环径向和轴向的三维分布，对教学和实际工程应用具有一定的指导作用。

1对载流圆环产生的磁场进行数学建模

设载流圆环的半径为R，其中通有电流为I。如图1所示，设载流圆环位于y-z平面上，圆心与坐标原点重合，载流圆环中心轴线与x轴重合。

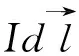
(1)

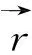
由磁场的叠加原理，则P点的磁感应强度为

(2)

因为直接求取该积分计算过程复杂且易出错，所以为了简化计算过程，我们在空间直角坐标系中，首先分别求取在x轴，y轴，z轴的磁感应强度分量，然后求矢量和得P点的磁感应强度，最后绘制磁场分布图，分析载流圆环在全空间的磁场分布特点。

(3)

(4)

将式(2) (3) 代入式(1)，其中

(5)

所以P点的磁感应强度分量为：

(6)

(7)

(8)

2基于MATLAB编写载流圆环产生磁场的仿真程序

在建立了载流圆环产生的磁场数学模型[9]后,根据上述分析建立的数学模型利用MATLAB软件编写可仿真、可执行的仿真程序。仿真程序[10]如下：

2.1初始化

根据式(6)～(8)，设置相关变量参数：

%用毕奥-萨伐尔定律计算电流环产生的磁场

clear all;%初始化，给定圆环半径、电流

mu0=4*pi*1e-7;%真空磁导率

I0=10.0；Rh=1;%圆环半径、电流

C0=mu0/(4*pi)*I0;%组合常数

NGx=21;NGy=21;%设定观测点网格数

x = linspace(-3,3,21);%设定观测点范围

y=x；z=y;

2.2求P点磁感应强度

利用分段求和的思想，求取空间任意一点P的磁感应强度：

Nh =20;%电流环分段数

theta0=linspace(0,2*pi,Nh+1);%环的圆周角分段

theta1=theta0(1:Nh);

y1=Rh*cos(theta1);z1=Rh*sin(theta1);%环各段的向量的起点坐标y1,z1

theta2=theta0(2:Nh+1);

y2=Rh*cos(theta2);z2=Rh*sin(theta2);%环各段的向量的终点坐标y2,z2

dlx=0；dly=y2-y1;dlz=z2-z1;%计算环各段向量dl的三个长度分量

xc=0；yc=(y2+y1)/2；zc=(z2+z1)/2;%计算环各段向量中点的三个坐标分量

for i=1:NGy%循环计算各网格点上的B(x,y)值

for j=1:NGx

rx=x(j)-xc;ry=y(i)-yc;rz=0-zc;%观测点在z=0平面上

r3=sqrt(rx.^2+ry.^2+rz.^2).^3;%计算r3

dlXr_x=dly.*rz-dlz.*ry;%计算叉乘积

dlXr_y=dlz.*rx-dlx.*rz;

Bx(i,j)=sum(C0*dlXr_x./r3);%把环各段产生的磁场分量累加

By(i,j)=sum(C0*dlXr_y./r3);

end

end

2.2绘制磁场分布矢量图：

空间任意一点P的磁感应强度计算出来后，可以绘制磁场分布矢量图，利用quiver命令绘出图形：

%磁场分布矢量图：

quiver(x,y,Bx,By);xlabel('x轴','FontSize',12')；ylabel('y轴','FontSize',12')；

title('圆环电流产生的磁场分布矢量图','FontSize',16);%用quiver画磁场矢量图

text(-0.15,1.2,'fontsize{30}o');text(0,1,'fontsize{30}.');

text(-0.15,-1.1,'fontsize{30}o');text(-0.15,-1.1,'fontsize{22} imes');

2.3绘制轴线上磁场分布图：

空间任意一点P的磁感应强度计算出来后，同样也可以绘制轴线上磁场分布图，根据磁场分布的对称性可以得出轴线上磁感应强度仅有Bx分量，By分量矢量和为零。利用plot命令绘出曲线：

%轴线上磁场分布：

plot(x,Bx)；xlabel('x轴','FontSize',12) ；ylabel('磁场x方向分量Bx','FontSize',12);

title('圆环电流轴线上的磁场分布图','FontSize',16);%x轴线上Bx分布

2.4绘制与圆环平行的平面磁场分布图：

空间任意一点P的磁感应强度计算出来后，可以绘制与圆环平行的平面磁场分布图，分别绘制距离载流圆环面距离为0,0.2,0.5,0.8,1.2,4(单位：m)处的磁场Bx分量，By分量分布图。利用surfc命令绘出曲面图：

%在与圆环平行的平面x=0,0.2,0.5,0.8,1.2,4上的磁场(包括Bx,By)分布

surfc(y,z,Bx)；xlabel('y轴','FontSize',12')；

ylabel('z轴','FontSize',12');zlabel('磁场x方向分量Bx');

title('圆环所在平面x=0上磁场x方向分量Bx分布图','FontSize',16);

%y-z面上Bx分布

surfc(y,z,By)；xlabel('y轴','FontSize',12')；

ylabel('z轴','FontSize',12');zlabel('磁场y方向分量By');

title('圆环所在平面x=0上磁场y方向分量By分布图','FontSize',16)；

%y-z面上By分布

2.5绘制与圆环垂直的平面磁场分布图：

空间任意一点P的磁感应强度计算出来后，同时也可以绘制与圆环垂直的平面磁场分布图，即x-y平面上的磁场Bx分量，By分量分布图。利用surfc命令绘出曲面图：

subplot(1,2,1);

surfc(x,y,Bx);

xlabel('x轴','FontSize',12')；ylabel('y轴','FontSize',12');zlabel('磁场x方向分量Bx');

title('与圆环垂直z=0面上磁场x方向分量Bx分布三维图','FontSize',12);

subplot(1,2,2);

plot(x,Bx);

xlabel('x轴','FontSize',12') ；ylabel('磁场x方向分量Bx');

title('与圆环垂直z=0面上磁场x方向分量Bx沿x方向分布图','FontSize',12);

%x-y面上Bx分布

subplot(1,2,1);

surfc(x,y,By);

xlabel('x轴','FontSize',12')；ylabel('y轴','FontSize',12');zlabel('磁场y方向分量By');

title('与圆环垂直z=0面上磁场y方向分量By分布三维图','FontSize',12)；

subplot(1,2,2);

plot(x,By);

xlabel('x轴','FontSize',12') ；ylabel('磁场y方向分量By');

title('与圆环垂直z=0面上磁场y方向分量By沿x方向分布图','FontSize',12);

%x-y面上By分布

在程序%后面是程序的说明部分，仿真程序编写完成后保存为zlyhcc.m。

3圆环电流产生磁场的仿真结果和分析

运行zlyhcc.m仿真程序不同部分后，得到仿真结果如下所示。

3.1磁场矢量图

分析：由图2看出，圆环电流磁场分布符合右手螺旋定则，线圈附近磁感线密集，磁感应强度大，而离线圈越远，磁感线稀疏，磁感应强度变小。此外，该图为过圆环中心与圆环面垂直的平面上磁场分布图，该图绕轴线旋转即可得到磁场的空间分布图形。

3.2圆环电流中心轴线上磁场分布

分析：由图3看出，圆环电流轴线上磁感应强度关于圆环所在平面对称，大小、方向均相同；而且轴线上圆环中心处磁感应强度最强，随距离圆环中线越远，磁感应强度越弱。

3.3与圆环平行的平面磁场分布

3.3.1与圆环平行的平面磁场Bx分布

分析：由图4看出，圆环电流在与圆环面平行的面上的磁感应强度Bx分量。

与圆环面平行的面离圆环面距离很近时，圆环周围磁感应强度大，大于中心轴线上磁感应强度；而离圆环面距离稍远，大于圆环半径时，与圆环面平行的面上中心轴线上磁感应强度最大，大于该面上其他任意位置处的磁感应强度，且随着距离增大，磁感应强度减小11-14]。

3.3.2与圆环平行的平面磁场By分布

分析：由图5看出，圆环电流在与圆环面平行的面上的磁感应强度By分量：无论与圆环面平行的面距离圆环面远近，中心轴线上磁感应强度都为0，其他位置磁感应强度关于中心轴线成中心对称分布。

3.4与圆环垂直的平面磁场分布

分析：由图6、图7看出，圆环电流在与圆环面垂直的面上的磁感应强度：无论与圆环面平行的面距离圆环面远近，中心轴线上磁感应强度By分量都为0，只有Bx分量，且随着距离增大，磁感应强度减小；越靠近圆环，磁感应强度越大。

4总结

通过利用MATLAB软件分段求和，计算载流圆环空间任意一点的磁感应强度，绘制磁场分布矢量图、中心轴线上磁场分布图、与圆环面平行及垂直的面上磁场分布图，不仅直观反映了圆环电流在空间产生的磁场分布规律，而且可以通过设置圆环线圈匝数、电流、半径等参数，定量计算磁感应强度具体大小，这在实际工程应用或者物理学研究教学方面都有十分重大的意义。

参考文献：

[1]贾瑞皋,薛庆忠.电磁学[M].北京：高等教育出版社,2011:161-164.

[2]向裕民.圆环电流磁场的普遍分布[J].大学物理,1999,01:16-19.

[3]罗宏超,蔡敏.圆电流全空间磁感应强度B的分布[J].沈阳航空工业学院学报,2006(1):79-80+91.

[4]朱平.圆电流空间磁场分布[J].大学物理,2005(9):13-17.

[5]刘保义,张明霞.圆环电流在全空间形成的磁感应强度分布[J].天水师范学院学报,2009(2):65-66.

[6]王晓颖,李武军.载流圆环空间磁场分布的研究[J].西安工业学院学报,2004(3):292-295.

[7]陈丽群.圆形载流线圈磁场的空间分布[J].娄底师专学报,2000(4):77-79.

[8]王玉梅,孙庆龙.利用MATLAB分析圆环电流的磁场分布[J].长春师范学院学报:自然科学版,2010(2):20-23.

[9]陈怀琛.Matlab及其在理工课程中的应用指南[M].西安:西安电子科技大学出版社,2004:292-295.

[10] 司文建,周楠,曹玉松.基于MATLAB的亥姆霍兹线圈轴线磁场均匀分布的动态仿真[J].许昌学院学报,2010(5):72-74.

[11] Byrd P F,et al.Handbook of Ellptic Integrals for Engineers and Physicists[M].Berlin:springer-Verlag,1954.8-13.

[12] G reenhillA G.The application of elliptic functions.New York:Dover,1959.

[13] 王明美.利用“几何画板”探索螺线管的磁场分布[J].大学物理实验，2015，28(5)：57-59.

[14] 罗浩，向泽英，谢英英，等.霍尔效应法测磁场实验误差研究[J].大学物理实验，2015(4)：99-102.

Dynamic Simulation of Distribution ofMagnetic Filed about a Current-Carrying Coil Based on MATLAB

XU Sheng-nan，REN Xue-zhi，WEI Hao-jie，ZHAN Cai-yun，CHEN Wen-juan

(China University of Petroleum,Shandong Qingdao 266580)

Key words：Biot-Savart law；current-carrying coil；MATLAB；magnetic induction

Abstract：According to Biot-Savart Law,the integral representation of the magnetic field distribution of a current-carrying coil is derived.The computed results are given by using with MATLAB and the simulations of the vector graphy of magnetic field distribution,the graphs of magnetic field distribution on the central axis,in the surface which is parallel to the coli and the surface which is vertical to the coli are carried out.The three-dimensional distribution of the magnetic filed in the radial and axial direction is studied,which plays a guiding role in education and application of practical engineering.

收稿日期：2016-01-30

基金项目：中国石油大学(华东)教学研究与实践项目(QN201531)；中国石油大学(华东)精品实验项目(JS 201415)；中国石油大学(华东)大学生创新创业训练项目

文章编号：1007-2934(2016)03-0096-07

中图分类号：TP 391.9

文献标志码：A

DOI：10.14139/j.cnki.cn22-1228.2016.003.026