两个线性变量实验数据处理的研究

陈　璐

(岭南师范学院，广东 湛江　524048)



两个线性变量实验数据处理的研究

陈璐

(岭南师范学院，广东 湛江524048)

摘 要：对实验数据处理中经常遇到的线性参数估计和作为间接测量量计算的问题进行了分析、比较。指出最小二乘参数不确定度不同时应该使用不同的对应公式，如果此情况下将参数作为间接测量量计算，往往更方便、简单。

关键词：数据处理；线性参数估计；最小二乘法；间接测量量

对两个变量x、y进行线性拟合和参数估计在实验中经常遇到。但线性参数估计和线性拟合应该是两个概念。线性拟合的目的是寻求y与x之间的函数关系或验证它们之间的线性关系，线性参数估计的目的则是在假设y与x之间为线性关系y=a+bx时求出参数a、b的最佳估计值。对同一组实验数据，目的不同，处理方法也应该不同。本文提出了同一组数据的3种处理方法，进行了分析、比较。

1理论分析

两个线性变量x，y的n组测量值(xi,y)，如果xi足够准确，yi为等精度测量、没有或消除了系统误差，则由

y=a+bx

(1)

用最小二乘法原理可得到参数a、b的最佳估计值[1]

(2)

(3)

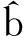
(4)

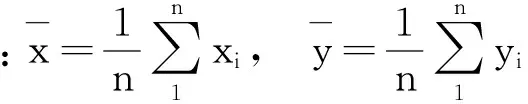
(5)

(6)

(7)

(8)

从数学上看，(3)式与(6)式的差别仅在于解正规方程

(9)

(10)

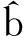
(11)

另一方面，如果在此情况下将参数b作为间接测量量对待，把每组测量值(xi,y)直接代人(1)式，就可得到一个对应的bi，因为每组测量量是相互独立的，bi计算结果的分布也应该是随机分布或近似正态分布，所以b的最佳估计值及其标准偏差也可用下式计算：

(12)

相对而言，(12)式的计算较为简单、直观。

2实验及应用

为了对上述三种数据处理方法进行比较，使用文献[3]或[4]的数据。

用伏安法测电阻，测得数据为[3-4]

方法1：直接用最小二乘法公式，由(3)、(4)、(5)式，得：

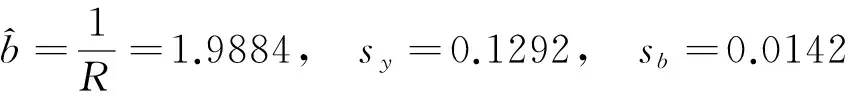
方法2：将参数a(=0)作为已知测量量，由(6)、(7)、(8)式，得：

方法3：将参数b作为间接测量量，由数据表(第三行)和(12)式，得：

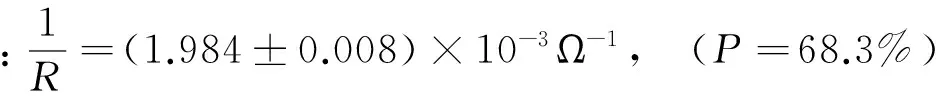
明显看出，在相同置信概率情况下，方法2和方法3好于方法1，而方法3与方法2相当，但计算相对简单。

由此，我们觉得应把线性参数估计与线性曲线拟合两个概念区分开来[5-7]，不宜用统一公式处理。即便是同一组数据，目的不同，处理方法也应不同。如上面的例子中，如果目的是测电阻，则应该用(6)式或(12)式，即方法2或方法3，如果目的是寻找电流与电压的关系，或验证欧姆定律，则应该用(2)、(3)式，即方法1。这主要是因为，进行线性参数估计时，这种做法本身就意味着假设函数关系y=a+bx(1)式是绝对正确的(如它已由理论和大量实验和经验证实)，我们的目的只是寻求参数a和b的最佳估计值(数学期望值)，所以在a为已知时，最好用(5)式或(12)式估计b值；而如果我们的目的是寻找y与x之间的函数关系或验证它们之间的线性关系，则应该用(2)、(3)式，这步结束后，按道理还应对其进行线性统计假设的检验，即计算、分析关联系数。

3结论

双变量线性拟合和参数估计时应该根据目的不同使用不同数据处理方法。最小二乘参数公式适用于二变量线性拟合问题，但当已知二变量为线性关系、参数a的不确定度远高于b的不确定度情况时，b的最佳估计值应该使用不同公式计算，如果此情况下将参数b作为间接测量量计算，往往更简单、方便。

论文得到陈冠英教授的悉心指导，深表谢意。

参考文献：

[1]杨述武.普通物理实验(二、电磁学部分)[M].北京：高等教育出版社，2000：12-16.

[2]陈冠英.线性参数估计中一个值得注意的问题[J].物理实验，1991,11 (3):118.

[3]林抒,龚镇雄.普通物理实验 [M].北京：高等教育出版社，1981：33-42.

[4]吕斯骅,段家忯.基础物理实验 [M].北京：北京大学出版社，2002：74-77.

[5]迈耶P.L.，概率引论及统计应用[M].潘考瑞译.北京：高等教育出版社，1986：358-399.

[6]单明，聂燕平.线性拟合中的逐差法和最小二乘法的比较[J].大学物理实验，2005，18(2)：68-70.

[7]周玉珠，姜奉华.实验数据的一元线性回归分析及其显著性检验[J].大学物理实验，2001(4)：43-46.

Analysis of Two Linear Variable Experimental Data Processing

CHEN Lu

(Lingnan Normal University，Guangdong Zhanjiang 524048)

Key words：data processing；linear parameters estimation；least-square method；indirect measurements

Abstract：Often encountered in the experiment data processing of linear parameters estimation and which as the problem of the indirect measurements calculation are analyzed and compared.Points out for different least-squares parameter values of uncertainty should use different corresponding formula,and if this case as using indirect measurements of calculation,tend to be more convenient and simple.

收稿日期：2016-02-14

基金项目：岭南师范学院“创新强校工程”项目

文章编号：1007-2934(2016)03-0126-03

中图分类号：O441.1；O4-34

文献标志码：A

DOI：10.14139/j.cnki.cn22-1228.2016.003.033