基于数学思维与M cCabe方法的编程优化问题研究

祁俊，王璐，王晓青



基于数学思维与M cCabe方法的编程优化问题研究

祁俊，王璐，王晓青

摘 要：针对程序复杂度高的问题，提出在结构化程序设计中利用数学思维方法来进行代码剖析、发现客观规律并归纳抽象，从而实现编程优化的思路。结合McCabe方法对程序进行复杂度度量，来说明利用数学思维进行编程可以明显降低程序的复杂程度，达到编程优化的目的。

关键词：数学思维；McCabe方法；程序复杂度；编程优化

0 引言

计算机编程是软件开发的主要手段，编程质量直接影响着软件的质量。计算机科学是算法的科学，同一问题采用的算法多种多样，编写出的程序质量也有很大差距。体现一个程序员水平最重要的地方就是算法，一个好的算法使用非常少的代码就能实现原来很复杂的操作。在编程过程中只有选取高效的算法不断进行代码的优化才能提高程序的质量，其中衡量编程质量的重要指标之一是程序复杂度［1］。

程序复杂程度关系着程序编写难度，也关系着程序设计和程序测试的难度。度量程序复杂度的目的在于衡量软件人员的价值和软件价值。对于解决同一问题的不同程序代码，复杂度越低则程序价值越高，通用性越好。因此通过使用高效的算法对软件程序进行编程优化，降低程序复杂度来提高软件质量是软件编程人员一直以来追求的目标。

本文提出在结构化程序设计中通过利用数学思维对程序进行编程优化的思路，以达到降低程序复杂度，提高软件质量的目的。

1 数学思维编程优化思想

结构化程序设计的先驱Niklaus W irth提出著名公式“程序 = 算法 + 数据结构”，从中可以看出算法是程序设计的灵魂。算法和程序之间是密不可分的关系，没有算法就编不出好的程序［2］。对计算机编程优化起着至关重要的作用就是对于算法的选择。

根据维基百科的定义，算法可以理解为求解问题的具体过程、步骤、方法。常用的算法有：穷举法、递推法、递归法、迭代法等等。计算机编程过程中仅仅依靠常规算法进行编程并不能直接得到简洁、高效的程序代码，特别是对于需要多重循环、多重判断实现的算法而言，往往会带来程序复杂度高的问题，不利于提高软件的质量。因此编程过程中对于程序进行进一步的优化是非常有必要的。

万事万物都隐含着规律，我们发现结合实际问题利用数学思维观察程序代码，进行代码剖析，就可以发现代码中隐藏的规律。通过利用数学思维，科学的进行归纳和抽象就可以优化算法、简化代码、实现编程优化，达到降低程序复杂度的目的。

本文提出的数学思维编程优化的思想是在常规方法实现的代码基础上，利用数学思维结合实际问题，通过观察发现客观规律归纳出抽象模型从而实现编程优化的一种编程思路。在编程过程中利用数学的思维和理论来解决实际问题，研究和分析实际问题的本质，以及隐含的规律，经过抽象转化为合理的数学结论。通过利用数学的思想和方法进行分析、探讨、研究，最终实现编程优化的目的。整个过程大致可分为三步，如图1所示：

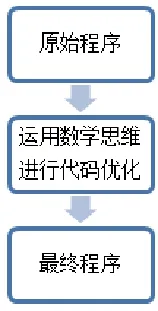
图1 编程优化过程

本文结合度量结构化程序复杂度的M cCabe方法来说明，利用数学思维进行编程优化可以显著提高程序的通用性和降低程序复杂程度。

2 结构化程序复杂性度量方法

M cCabe复杂性度量又称环路度量，是由Thomas M cCabe提出的一种基于程序控制流的复杂性度量方法。它认为程序的复杂性很大程度上取决于程序图的复杂性。单一的顺序结构最为简单，循环和选择所构成的环路越多，程序就越复杂。被认为是动态白盒测试技术中严谨而有效的测试方法［3］。M cCabe复杂度是用来衡量一个模块判定结构的复杂程度，数量上表现为独立现行路径条数，即合理的预防错误所需测试的最少路径条数［4］。显示了在测试一个单元时，为保证软件质量而需要测试的基本路径的最小数目［5］。复杂度高说明代码质量可能很差，难于测试和维护。根据经验，程序的可能错误和复杂度高有着很大关系［6］。

具体方法是先给出程序流程图，把每一个图框都认为是一个结点，得到计算M cCabe复杂度。如公式（1）：

V（ G） = m - n + p （1）

其中，V（G）表示初始框节点和结束框节点相连的程序图中线性无关环个数。 m 是有向图中的弧数，n 是有向图中的结点数，p 是图 G 中的强连通分量的个数。

由于McCabe方法是以图论为基础，所以通过程序的控制流图可以获得程序的复杂度，还可用以下3个数据表示［7］：

①流图中区域的数量；

②流图中边的数量－流图中节点的数量+2；

③流图中判定节点的数量+1。

虽然利用M cCabe方法可以度量程序的复杂度，但是需要编程人员在编程同时人工绘制程序流程图和程序图并计算出节点和边的个数，计算方式繁琐。所以我们利用改进的M cCabe 方法，如计算公式（2）：

V（ G） = M + N + 1 （2）

其中，M 为判断语句 （ if） 的个数； N 为循环的总重数［8］。该方法不用再绘制程序流程图，更加容易统计弧数和结点数。

根据改进M cCabe计算公式（2）可知数字1是常量，对于计算结果没有影响，所以本文是在公式（2）的基础上加以简化，如公式（3）：

V（ G） = M + N （3）

通过公式（3）可以更加方便快捷的计算出程序的复杂度。

3 数学思维编程优化实例

3.1 穷举法优化问题

穷举法是最基本的编程方法之一。穷举法主要是通过多重循环穷举来得出计算结果。而程序运行时间和循环重数成正比关系，过多的循环重数会极大降低程序的执行效率，所以在进行编程求解时要根据实际问题结合数学思维进行编程优化，从而达到降低程序复杂度提高程序通用性的目的。下面通过几个常见的问题进行说明。

百元买百鸡问题

百元买百鸡是一道古典数学问题，问题定义为：鸡翁一值钱五，鸡母一值钱三，鸡雏三值钱一，百元买百鸡，问鸡翁、鸡母、鸡雏各几何？

这道题可以利用计算机中的穷举算法来实现。具体编程中利用C语言中的for语句嵌套三层来实现。

代码片段如下：

利用改进的McCabe公式（3）可知：

V（ G） = M + N =1+3=4

通过观察，利用数学思维对程序进行优化。首先根据题意可推出公式（4）：

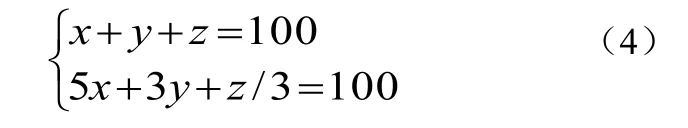
根据公式（4）可推出z=100-x-y，带入公式（4）化简可得：7x+4y=100。这样可以化简掉一重循环。沿着这个思路继续变换，可推出公式（5）：

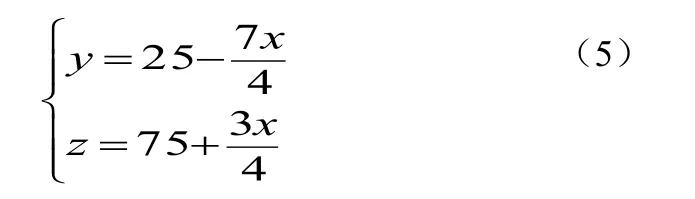
根据公式（5）来对程序进行编程优化，可将三重循环降为一重。同样从公式（5）可以观察得出x是4的倍数而x又不能超过20。程序代码片段如下：

通过数学思维进行编程优化后，将循环降为1重，并通过数学变换得出公式（5）后又可以省却了1重判断。McCabe方法度量可得出：

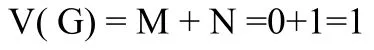
如表1所示：

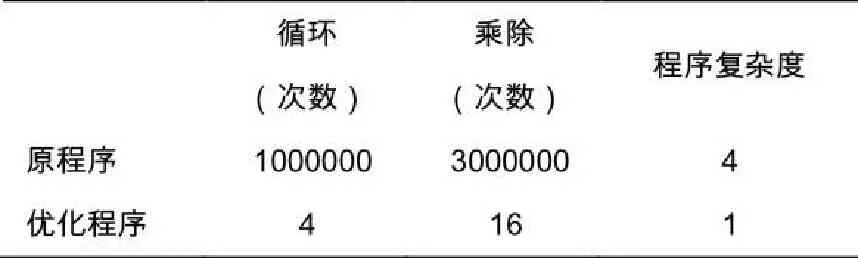
表1 优化前后程序对比

从表1可以看出，利用数学思维优化后的程序无论从程序循环次数还是复杂度都有了极大的优化。

求四位的卡普列加数问题

卡普列加数定义即：对n位自然数N，将N2切分为两半，右边n位为一个数，左边其余各位为另一个数，如果这两个数之和恰好等于N，那么称N和N2为一对卡普列加数，其中N为卡普列加底数，N2为卡普列加平方数。例如552=3025，30+25=55

同样通过常规编程可以用穷举法来实现，但需要设置4重循环来进行穷举，内层循环还需设置选择语句做判断。计算M cCabe环数可知：

V（ G） = M + N =1+4=5

多重循环会造成计效率低下，利用数学思维进行程序优化。如下：

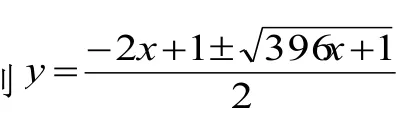
程序代码片段如下：

通过数学思维进行编程优化后，计算可知：

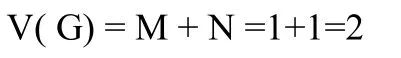
通过上例代码优化可以看出，程序复杂度从5降低到了2，循环的重数也从4重降低到了1重，循环次数大大减少，极大提高了程序执行效率，同时也降低了程序复杂度。

类似的穷举问题还有很多，特别是穷举循环嵌套层数过多，循环次数比较大的情况下，如果在编程中只是单纯的依靠多重循环嵌套让计算机去计算，势必带来程序复杂度和效率问题，这种算法就不能称之为好的算法。我们一定要利用数学思维归纳问题规律，对这类问题进行编码优化，才能实现降低程序复杂度，提高程序效率的目的。

3.2 分段函数问题

分段函数是一个重要的数学函数模型，在现实生活中处处可见。比如，税务计算、养老金核算、成本控制等。简单的问题可以用一元函数来解决，复杂问题就要用到多元函数。我们以求个人所得税问题来进行编程优化举例。假设个人所得税计算规则如下：

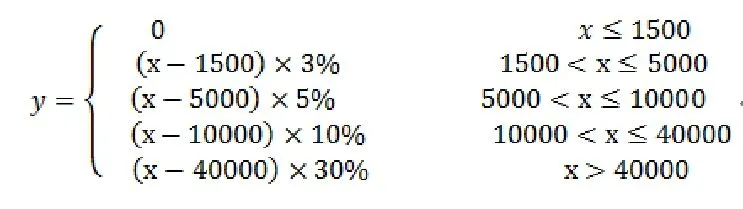
按照上式，可用多重if语句来实现求解。程序代码片段如下所示：

计算可知：

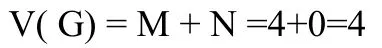
如果问题改变，则相应的if语句重数必定随之增加。程序复杂度也会随之加大。根据数学思维的思想，观察程序代码，得出假设：

a0=0，a1=1500，a2=5000，a3=10000，a4=40000；

b0=0，b1=0.03，b2=0.05，b3=0.1，b4=0.3；

则求解所得税就可以改为：

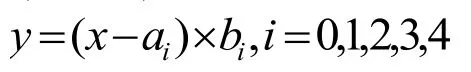
则程序代码片段如下：

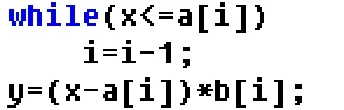
根据优化后的程序，计算可知：

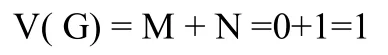
此外类似的例子还有很多，比如求养老金保险问题、行李寄存问题等等。这些问题都可以利用数学思维编程优化的思想，通过观察、归纳、抽象改为非常简单的问题求解来进行编程实现，极大降低了圈环重数。即使程序问题规模变大，也只需要改动数据即可，而不需要改动程序，降低程序复杂度的同时也极大提高了程序的通用性。

4 总结

随着计算机软件的不断发展，人们编写的程序也越来越复杂，越来越庞大。随之带来的隐含错误也越来越多，花费在程序调试、测试和维护的代价甚至要占到总成本的70%以上，所以要减少程序的隐含错误，便于测试和维护，就要从编程优化、降低程序复杂度着手。在计算机编程中通过数学思维能够把复杂的代码高度抽象和归纳，从而优化代码，大大加快计算机程序的运行时间，提高计算机执行程序的效率，是计算机编程优化和降低程序复杂度的关键。在实际的编写程序过程中要充分的发挥数学思维对计算机编程的优化作用。融入数学思维的编程思想，就是通过不断地剖析、归纳和抽象程序的算法，而使计算机编程得到优化的过程。在编程过程中，编程人员要善于发现，总结归纳问题的隐含规律。利用数学思维以数学科学的思维和角度去看待问题，从而在计算机编程的世界里找到一把开启优化的钥匙。

参考文献

［1］ 覃征，虞凡，王志敏，杨博.程序设计方法与优化［M］.西安:西安交通大学出版社，2007.

［2］ 齐悦，夏克俭，姚琳.数据结构、算法与应用［M］.北京:清华大学出版社，2015 .

［3］ WIJAYASIRIWARDHANET K，WIJAYARATHNA P G，KARUNARATHNA D D. An automated tool to generate test cases forperform ing basis path testing ［C］//ICTer 2011: Proceedings of the2011 International Conference on Advances in ICT for Emerging Regions.Piscataway: IEEE Press，2011: 95-101.

［4］ 朱鸿，金凌紫.软件质量与保证 ［M］. 北京:科学出版，1997.

［5］ 樊庆林，吴建国.提高软件测试效率的方法究［J］ .计算机技术与发展，2006，16（10）:52-54

［6］ 黄华林.使用 M cCabe IQ提高测试质量的研究［J］.微型机与应用，2012（31）:69-70.

［7］ 王 敏，陈少敏，陈亚光.基本路径测试用例设计算法，［J］计算机应用，2013，33（11）:3262-3266.

［8］ 王冠，景小宁，王彦军.基本路径测试中的McCabe 算法改进与应用，［J］哈尔滨理工大学学报，2010（15）:48-51.

Research on Programm ing Optim ization Based on M athematical Thinking and M cCabe M ethod

Qi Jun， Wang Lu，Wang Xiaoqing
（Department of Computer Technology and Application， Qinghai University， Xining 810016， China）

Abstract:To aim at the high complexity of the program， it uses mathematical thinking method in the process of structural design to analyze the code and find the objective laws， so as to achieve the idea of programming optim ization. Using the M cCabe method to measure the complexity of the program， it can be used to reduce the complexity of the program and achieve the purpose of programm ing optim ization by programm ing w ith mathematical thinking.

Key words:Mathematical Thinking； M cCabe Mothed； Program Complexity； Programm ing Optimization

中图分类号：TP312

文献标志码：A

文章编号：1007-757X（2016）05-0020-03

基金项目：青海大学中青年科研基金项目（2015-QGY-11）；青海大学课堂教学改革和考试综合改革项目（KG-14-04）

作者简介：祁 俊（1977-），女，青海贵德，青海大学计算机技术与应用系，副教授，硕士，研究方向：智能信息处理、计算机教育，西宁 ，810016 王 璐（1984-），女，河北廊坊，青海大学计算机技术与应用系，讲师，硕士，研究方向：数据挖掘，西宁，810016王晓青（1964-），女，陕西彬县，青海大学计算机技术与应用系，教授，学士，研究方向：计算机教育，西宁，810016

收稿日期:（2015.12.02）