核矩阵协同进化的震荡搜索粒子群优化算法

戴月明,朱达祥,吴定会

(江南大学 物联网工程学院, 江苏 无锡214122)



核矩阵协同进化的震荡搜索粒子群优化算法

戴月明,朱达祥,吴定会

(江南大学 物联网工程学院, 江苏 无锡214122)

摘要：针对粒子群算法搜索后期易陷入局部极值的缺点，提出一种基于核矩阵协同进化的震荡搜索粒子群优化(kenel matrix synergistic evolution shock search particle swarm optimization,KMSESPSO)算法，该算法对粒子进行局部与全局结合的震荡搜索，且当整个粒子种群陷入停滞状态时，利用核矩阵对特定粒子组进行协同进化以扩大种群的多样性。实验结果表明，KMSESPSO算法有效提高了粒子的全局搜索能力，既避免粒子种群易早熟收敛, 又较好地提高寻优精度、加快收敛速度，且有一定的鲁棒性。

关键词：粒子群优化算法；震荡搜索；核矩阵；协同进化

0引言

粒子群优化算法(particle swarm optimization，PSO)是由J Kennedy和R C Eberhart在1995年首次提出的一种经典群体智能算法，采用基于种群的全局策略，算法的主要思想是模拟整个鸟群体觅食的过程，通过每个鸟个体之间的相互合作联系取得最优效果[1]。

为改善粒子群算法的性能，提升寻优效果，大量学者做出了努力。刘建华等[2]对离散二进制粒子群算法进行研究和分析，保持了原算法的全局探索能力，提高了种群的局部探测性；Arumugam等[3]借鉴遗传算法中交叉操作思想让2个父代通过某种方式交叉产生新的子代，这在一定程度上提升解的分布性；任子晖等[4]对基本粒子群优化算法进行理论分析，提出了一种加速收敛的粒子群优化算法，具有一定的高效性和稳健性；颜惠琴等[5]将基于高斯扰动的量子粒子群算法应用到图像分割领域，新算法的聚类效果和性能有明显改善；黄泽霞等[6]提出一种惯性权自适应调整的量子粒子群优化算法，动态地调整惯性权值,从而使算法具有动态自适应性；胡旺等[7]提出基于Pareto熵的多目标粒子群优化算法，引入格占优和格距离密度的概念，新算法表现出了显著的性能优势。标准的粒子群优化算法存在一定缺陷，为了改进算法的收敛速度和寻优精度，本文提出基于核矩阵协同进化的震荡搜索粒子群优化算法。新算法提出震荡锚点的概念，种群中的粒子围绕不同维度的震荡锚点做既全局又局部的震荡搜索。当最优粒子停滞代数大于设定的阈值时，对最优粒子进行基于拉普拉斯核矩阵和高斯核矩阵的协同进化，提升种群的多样性。算法结构简单，实现难度不大，并且在典型测试函数上的仿真实验结果显示，算法有着较好的跳出局部极值的能力和较快的收敛速度。

1标准的粒子群优化算法

假设一个粒子种群的规模为N，粒子在D维的搜索空间以初始速度V0开始飞行。粒子i的位置为xi=(xi1,xi2,…,xiD)，速度为vi=(vi1,vi2,…,viD)。截止到第t次迭代，粒子个体所找到的历史最优极值为pbi(i=1,2,…,N)，整个种群所找到的全局最优值为gbi。每一轮粒子的进化公式为

vi(t+1)=w×vi(t)+c1×rand1×

(1)

(2)

(1)-(2)式中：t是种群当前的迭代轮数；c1和c2是学习因子，它们是非负常数，一般取c1=c2=2，通过改变学习因子的值可以调节粒子的社会经验和自身经验对粒子寻优的影响度；rand1和rand2是[0,1]的随机数；w是惯性权重，它是非负常数。惯性权重线性递减策略为

(3)

(3)式中：t为当前的迭代次数；ωmax表示惯性权重的初始值；相应地ωmin则表示迭代终止轮数时惯性权重；Tmax表示迭代次数的上限值。

2核矩阵协同进化的震荡搜索粒子群优化算法

由于粒子群算法搜索后期经过多次迭代易陷入局部极值，提出一种基于核距阵协同进化的震荡搜索粒子群优化(kemelmatrixsynergisticevolutionshocksearchparticleswarmoptimization,KMSESPSO)算法。

2.1免疫进化思想以及对算法的启示

免疫进化算法[8]的核心在于尽可能利用当前种群最优个体的进化趋势替代整个种群。从统计学来说，与当前最优粒子之间空间距离小的粒子个体的适应度值要优于那些远离当前最优粒子的个体。另一方面，当前种群的全局最优粒子和最优解之间的距离小于其他粒子和最优解之间的距离的概率也较大。尽可能利用当前种群的全局最优粒子来描述问题特征。针对多峰函数及含有局部最优解的问题，在信任当前全局最优粒子的基础上，还要增加与种群中其他粒子的联系，种群的信息尽量由多个粒子的空间状态描述，而非仅一个当前全局最优粒子。

标准粒子群算法后期易陷入早熟收敛，而由于算法的局限性导致未能更精确地接近甚至找到这个最优解。由免疫进化得到的启示，充分利用优秀粒子个体信息，本文提出了一种新的进化策略，即当算法陷入停滞时，对当前的全局最优粒子和最接近全局最优粒子的若干个粒子进行基于拉普拉斯核矩阵和高斯核矩阵的协同进化，如果协同进化未提高粒子的适应度，则取消进化。具体的粒子个体数由核矩阵的维数来确定。

2.2核矩阵协同进化

2.2.1拉普拉斯核矩阵

二维拉普拉斯方程的微分形式为

(4)

(5)

由(5)式，我们定义拉普拉斯核矩阵为

(6)

(6)式中:DK是矩阵基础系数，决定了当前全局最优粒子在协同进化过程中的局部侵占率；Lx,y为拉普拉斯核矩阵第x行y列的值。

2.2.2高斯核矩阵

N维空间正态分布方程为

(7)

在二维空间的定义为

(8)

由(8)式，我们定义高斯核矩阵为

(9)

(9)式中:σ是高斯核矩阵的方差；k是高斯核矩阵的维数，它决定了当前全局最优粒子在协同进化过程中全局侵占率；Gx,y是高斯核矩阵第x行第y列的值。

2.2.3协同进化

拉普拉斯核矩阵是固定的3×3方阵，DK越小，局部侵占率越大，即当前全局最优粒子对协同进化的局部搜索性能影响越大。高斯核矩阵是动态的(2k+1)×(2k+1)方阵，k越大，全局侵占率越小，即当前全局最优粒子对协同进化的全局搜索性能影响越大。DK和k可由对当前种群全局最优粒子的信赖值调节，信赖值越高，则DK应越小；信赖值越低，则k应越大。协同进化的方式为

(10)

(10)式中：Sp表示协同因子；gbold表示进化前的全局最优粒子；L表示拉普拉斯核矩阵；G表示高斯核矩阵；gbnew表示全局最优粒子进化后的状态。

2.3核矩阵协同进化的震荡搜索粒子群优化算法

内嵌区域震荡搜索算法(regionshockparticleswarmoptimization,RSPSO)[9]粒子是以pi=(pi1,pi2,…,piD)为吸引子[10]，迭代过程中不断向其靠近，其坐标为

(11)

或者

(12)

(13)

(11)式中,r1,r2是(0,1)均匀分布的随机数。

在整个种群粒子的寻优过程中，粒子个体的速度逐渐减小，粒子i以一种趋向性靠近pi点，最后跌落在pi点。算法的主要思想是粒子i以吸引子为中心，以当前所处位置和该粒子吸引子间的距离Δi,j(t)(1≤i≤N,1≤j≤D)为震荡因子进行震荡搜索。

(14)

(15)

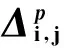
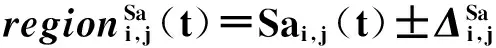
(16)

粒子的各个维度局部震荡搜索和全局震荡搜索一次，其在整个搜索空间的位置更新公式为

(17)

(17)式中：xi,j(t)为粒子的初始位置；dir确定粒子某个时刻的震荡方向。搜索的过程是针对粒子的每一个维度，先对当前的维度进行局部震荡搜索，计算出粒子的局部搜索适应度值，再对当前的维度进行全局震荡搜索，计算全局搜索适应度值，通过比较局部搜索适应度值和全局搜索适应度值确定粒子在该维度上的最佳位置，按此方法迭代搜索粒子的其他维度，直到找到每一个维度适应度最小的位置。融合各维度最佳粒子，若适应度值高于历史最优极值，则替换掉震荡搜索前的历史最优极值；若适应度值高于种群全局最优粒子的适应度值，则替换为新的全局最优值。

为了使粒子群算法能最大限度地避免陷入早熟收敛以及获得更好的寻优效果，本文提出了基于核矩阵的协同进化。进化策略为：当算法进入停滞状态，找出和当前全局最优粒子最接近的U个粒子，U=核矩阵维数-1。它们和全局最优粒子合并为进化粒子组(evolutionparticlegroup)。使用核矩阵对进化粒子组进行协同进化，如果进化后的全局最优粒子的解更优则进化成功，否则进化失败，恢复粒子组进化前的状态。

综上所述，算法的流程描述如下

步骤1生成种群及设置算法有关参数。种群规模为N，粒子个体的维度为D，拉普拉斯核矩阵的基础系数为DK，高斯核矩阵的维数为k，协同因子为Sp，最大迭代次数为IMax，粒子围绕震荡锚点震荡搜索次数为GS。

步骤2确定震荡锚点，由(11)式寻找当前粒子相应维数的吸引子以及当前的全局最优粒子。

步骤3进行迭代，对各粒子围绕震荡锚点进行震荡搜索。

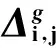
步骤3.3粒子各维度由(17)式进行既局部又全局的线性震荡搜索。

步骤3.4比较全局震荡搜索和局部震荡搜索所得适应度值，确定粒子在该维度上最佳适应度值的位置。

步骤4既局部又全局的震荡搜索之后，确定粒子个体新的局部最优粒子pbi和整个种群全局最优粒子gb。

步骤5当全局最优粒子的进化停滞，且迭代数大于一个阈值，根据(6)式和(9)式确定核矩阵，根据(10)式对进化粒子组进行基于核矩阵的协同进化，比较适应度值，如果更优秀就视为进化成功，否则取消进化。

步骤2至步骤5进行循环，直到找到最优解或者达到最大迭代次数。

3仿真实验结果及分析

为了检验KMSESPSO算法的寻优性能，本文采用表1中常用经典测试函数进行测试，且与标准粒子群优化算法、带有柯西变异的PSO算法[11]和内嵌区域震荡算法(RSPSO)测试结果作更直观的比较。

表1　经典测试函数及相关参数

表1中f6函数在对应30维时的理论最优值为-12 369.5，其他函数理论上的最优值均为0。

实验参数初始化：f1～f3函数中，种群规模N=10，f4～f8函数中，种群规模N=50。粒子维数和搜索范围由表1中指定。f4的最大迭代次数IMax=1 000，其他种群的最大迭代次数IMax=100。高斯核矩阵为3×3方阵，标准差σ为1，协同因子Sp=0.5。KMSESPSO提出了围绕震荡锚点做局部和全局的震荡搜索，即粒子在每次迭代的过程中，包含了一次的额外搜索，粒子迭代一次，其作用就相当于RSPSO迭代2次，因为存在着双重嵌套搜索，所以粒子群整体的搜索次数为GS=5。为尽可能地减少实验偶然性对结果的影响，用4种算法对选取的函数每个独立运行30次，取30次实验结果的平均最优适应度值和标准方差作为结果比较。

表2中的f1～f4均是单峰连续函数,相比其他3个算法，KMSESPSO表现出了很好的寻优效果。针对f1～f3函数,KMSESPSO的精度提升了几十甚至上百个数量级,算法的稳定性也有大幅度的提升, f2和f3函数的标准方差值小于Matlab的最小精度值,显示为0,说明具有很强的鲁棒性。针对f4函数,KMSESPSO在精度方面有数倍的增长。表3中的f5～f8均是多峰函数,在寻优过程中更易陷入局部极值。f5和f6函数收敛精度都有一定程度的提升, f7和f8的精度和标准方差超过了Matlab最小精度值,说明KMSESPSO算法有很好的稳定性。从仿真实验统计结果来看,KMSESPSO在单峰函数和多峰函数都能有效地避免陷入局部极值,展现出很强的全局寻优能力。

图1至图4分别是RSPSO和KMSESPSO算法在函数f1，f3，f5，f7上的收敛曲线，其中横坐标为整个种群当前进化的代数，纵坐标为粒子在当前代数对应的适应度值的自然对数。通过图1—图4可以明显看出，KMSESPSO算法的收敛曲线在算法初期就有比较大的变化趋势,达到相同精度的情况下所需迭代的轮数更小,即有着更快的收敛速度;在相同的迭代轮数,KMSESPSO具有更高的寻优精度。

仿真实验结果显示，对于选取的经典测试函数，KMSESPSO算法在收敛精度、收敛速度以及稳定性等方面都有着较好的寻优效果，算法性能评价指标优于其他参与实验的算法。以上实验结果充分验证了KMSESPSO算法的高效性和稳健性。

表2　算法在f1～f4上的平均最优值和标准方差

表3　算法在f5～f8上的平均最优值和标准方差

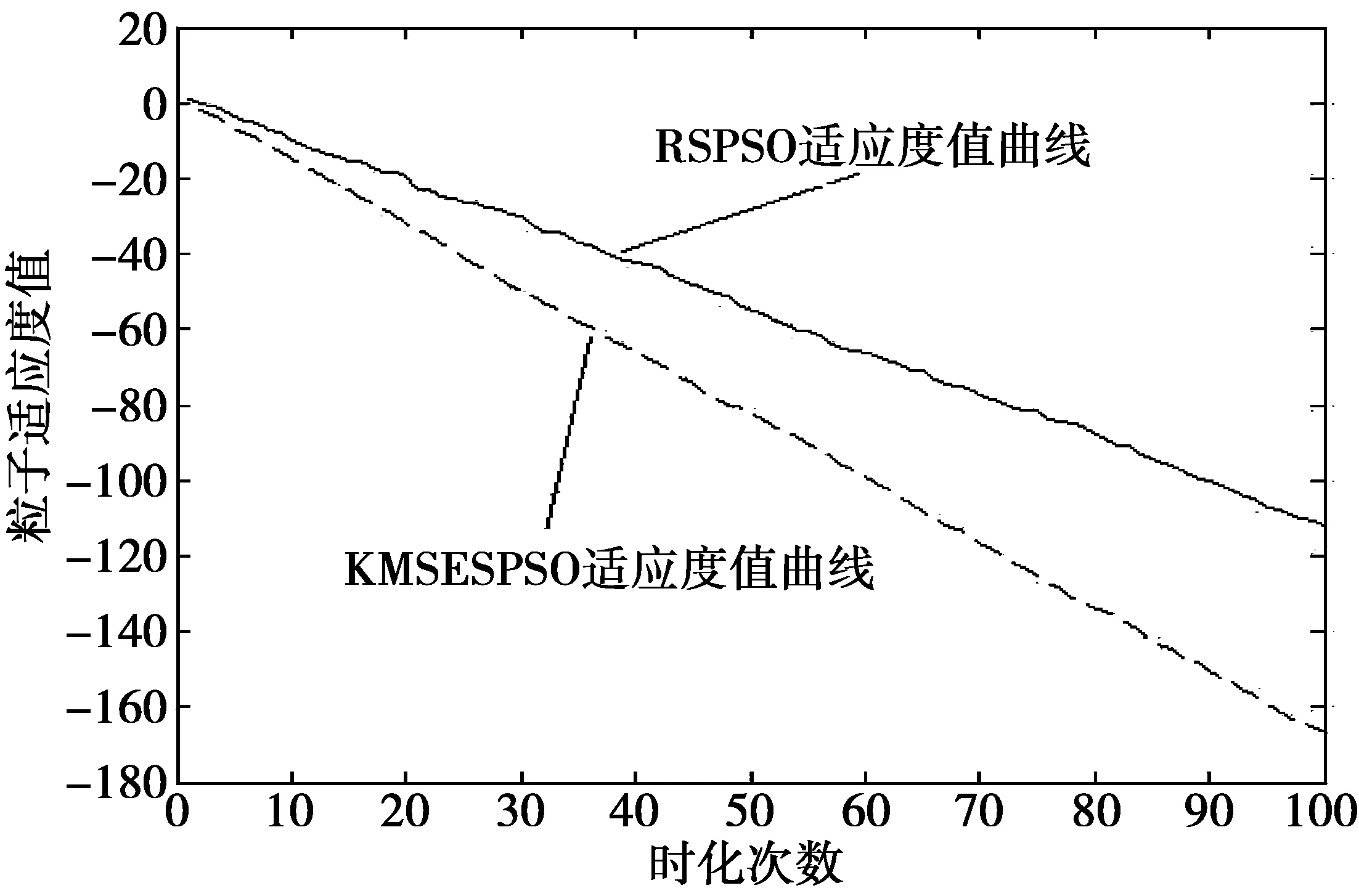
图1　在f1函数的运行结果Fig.1　Results on function f1

图2　在f3函数的运行结果Fig.2　Results on function f3

图3　在f5函数的运行结果Fig.3　Results on function f5

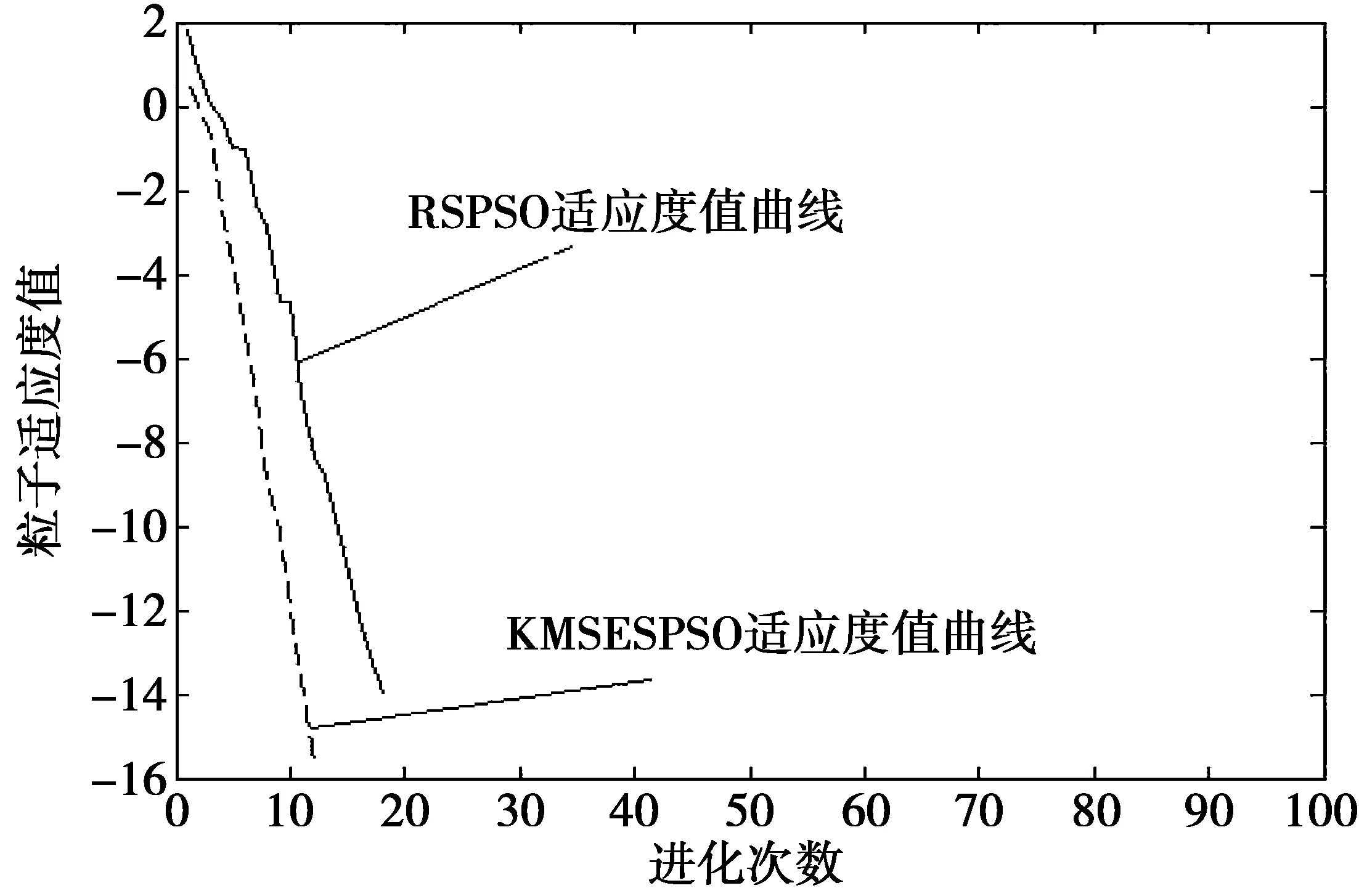
图4　在f7函数的运行结果Fig.4　Results on function f7

4结束语

基于核矩阵协同进化的震荡搜索粒子群优化算法在每一轮迭代过程中对粒子围绕震荡锚点进行既局部又全局的震荡搜索，提高了粒子全局寻优能力和收敛速度。利用拉普拉斯核矩阵和高斯核矩阵对算法后期陷入停滞状态的进化粒子组进行协同进化，提高了种群的多样性，有效地避免了整个种群陷入早熟收敛。仿真实验结果表明, 对于全部测试函数,基于核矩阵协同进化的震荡搜索粒子群优化算法能够有效避免局部极值, 得到全局最优值，在寻优能力、收敛速度、算法稳定性方面都有不同程度的提高，尤其是针对单峰连续函数的寻优性能提升显著。KMSESPSO也存在不足之处，在算法的震荡搜索过程中，目前是围绕该维度的震荡锚点线性等比例分配搜索点，存在一定的局限性，针对复杂的寻优问题如果要获得突出的效果，就需要增加震荡搜索的次数，随之算法的时间复杂度就会上升，影响性能。下一步的研究重点是利用当前粒子某维度的位置信息，粒子在多维度空间的位置信息以及群体的综合信息非线性且非固定比例分配搜索点；引入其他核矩阵进行实验，对比算法效果；以及考虑进一步减少空间复杂度和时间复杂度，并且将算法运用到实际过程中。

参考文献：

[1]KENNEDY J, EBERHART R C.Particle swarm optimization[C]// Proceedings IEEE International Conference on Neural Networks. Pertn:IEEE Press, 1995: 1942-1948.

[2]刘建华，杨荣华，孙水华. 离散二进制粒子群算法分析[J].南京大学学报,2011,47(5):504-514.

LIU J H, YANG R H,SUN S H.The analysis of binary particle swarm optimization[J]. Journal of Nanjing University,2011,47(5):504-514.

[3]ARUMUGAM M S, RAO M V C. On the improved performances of the particle swarm optimization algorithms with adaptive parameters,crossover operators and root mean square(RMS) variants for computing optimal control of a class of hybrid systems[J].Applied Soft Computing, 2008, 8(1):324-336.

[4]任子晖, 王坚. 加速收敛的粒子群优化算法[J].控制与决策,2011,26(2):202-206.

REN Z H, WANG J.Accelerate convergence particle swarm optimization algorithm[J]. Control and Decision, 2011, 26(2):202-206.

[5]颜惠琴, 吴锡生. 基于高斯扰动量子粒子群优化的图像分割算法[J].计算机仿真,2011,28(3):275-278.YAN H Q,WU X S.ImageSegmentation Based on Quantum-Behaved Particle Swarm Optimization with Gaussian Disturbance[J].Computer Simulation,2011,28(3):275-278.

[6]黄泽霞, 俞攸红, 黄德才. 惯性权自适应调整的量子粒子群优化算法[J].上海交通大学学报,2012,46(2):228-232.

HUANG Z X, YU Y H, HUANG D C.Quantum-Behaved Particle Swarm Algorithm with Self-adapting Adjustment of Inertia Weight[J].Journal of Shanghai Jiaotong University, 2012, 46(2): 228-232.

[7]胡旺, YEN G G,张鑫.基于Pareto熵的多目标粒子群优化算法[J]. 软件学报,2014,25(5):1025-1050.

HU W, YEN G G, ZHANG X. Multiobjective particle swarm optimization based on Pareto entropy[J]. Journal of Software, 2014,25(5):1025-1050.

[8]倪长健, 丁晶, 李祚泳.免役进化算法[ J] .西南交通大学学报, 2003, 38(1):87-91.

NI C J,DING J,LI Z Y. Immune Evolutionary Algorithm [J].Journal of Southwest Jiaotong University,2003, 38(1): 87-91.

[9]汤继涛, 戴月明.内嵌区域震荡搜索的粒子群优化算法[J].计算机工程与应用,2013,49(21):33-36.

TANG J T,DAI Y M. Regional shock search embedded Particle Swarm Optimization algorithm [J]. Computer Engineering and Applications, 2013, 49(21)：33-36.

[10] CLERC M，KENNEDY J.The particle swarm:explosion, stability,and convergence in a multi-dimensional complex space[J].IEEE Transactions on Evolutionary Computation, 2002,6(1):58-73.

[11] WANG H, LIU Y, LI C H,et al.A hybrid particle swarm algorithm with cauchy mutation[C]//Proceedings of IEEE Swarm Intelligence Symposium.Honolulu:IEEE Press,2007:356-360.

Shock search particle swarm optimization algorithm based on kernel matrix synergistic evolution

DAI Yueming, ZHU Daxiang, WU Dinghui

(School of Internet of Things Engineering, Jiangnan University, Wuxi 214122,P.R. China)

Abstract:Due to the shortcoming of particle swarm optimization(PSO) algorithm that it is often trapping in local optimum at the late stage, a kind of shock search PSO algorithm based on kernal matrix synergistic evolution(KMSESPSO) is proposed.The proposed algorithm does a combination of local and global shocks search and when the whole particle swarm is stagnant a specific particle group would have a synergistic evolution to enrich the diversity of population by using kernel matrix.The experiment results show that the proposed algorithm strengthens the global search capability of particles effectively and can not only get free from premature but also raise the optimal accuracy in faster convergence speed and have certain robustness.

Keywords：particle swarm optimization; shock search; kernel matrix; synergistic evolution

DOI：10.3979/j.issn.1673-825X.2016.02.017

收稿日期：2015-04-07

修订日期：2015-12-10通讯作者：朱达祥zdxever@sina.com

基金项目：国家863计划项目(2013AA040405)

Foundation Item：National High Technology Research and Development Program of China(863 Program)(2013AA040405)

中图分类号：TP18

文献标志码：A

文章编号：1673-825X(2016)02-0247-07

作者简介：

戴月明(1964-)，男，江苏无锡人，副教授，硕士生导师，主要研究领域为人工智能与模式识别、数据挖掘。Email：dym@jiangnan.edu.cn

朱达祥(1990-)，男，安徽马鞍山人，硕士研究生，主要研究领域为人工智能，软件工程。Email：zdxever@sina.com

吴定会(1970-) ，男，江苏无锡人，副教授，博士，主要研究领域为新能源与自动控制。

(编辑：张诚)