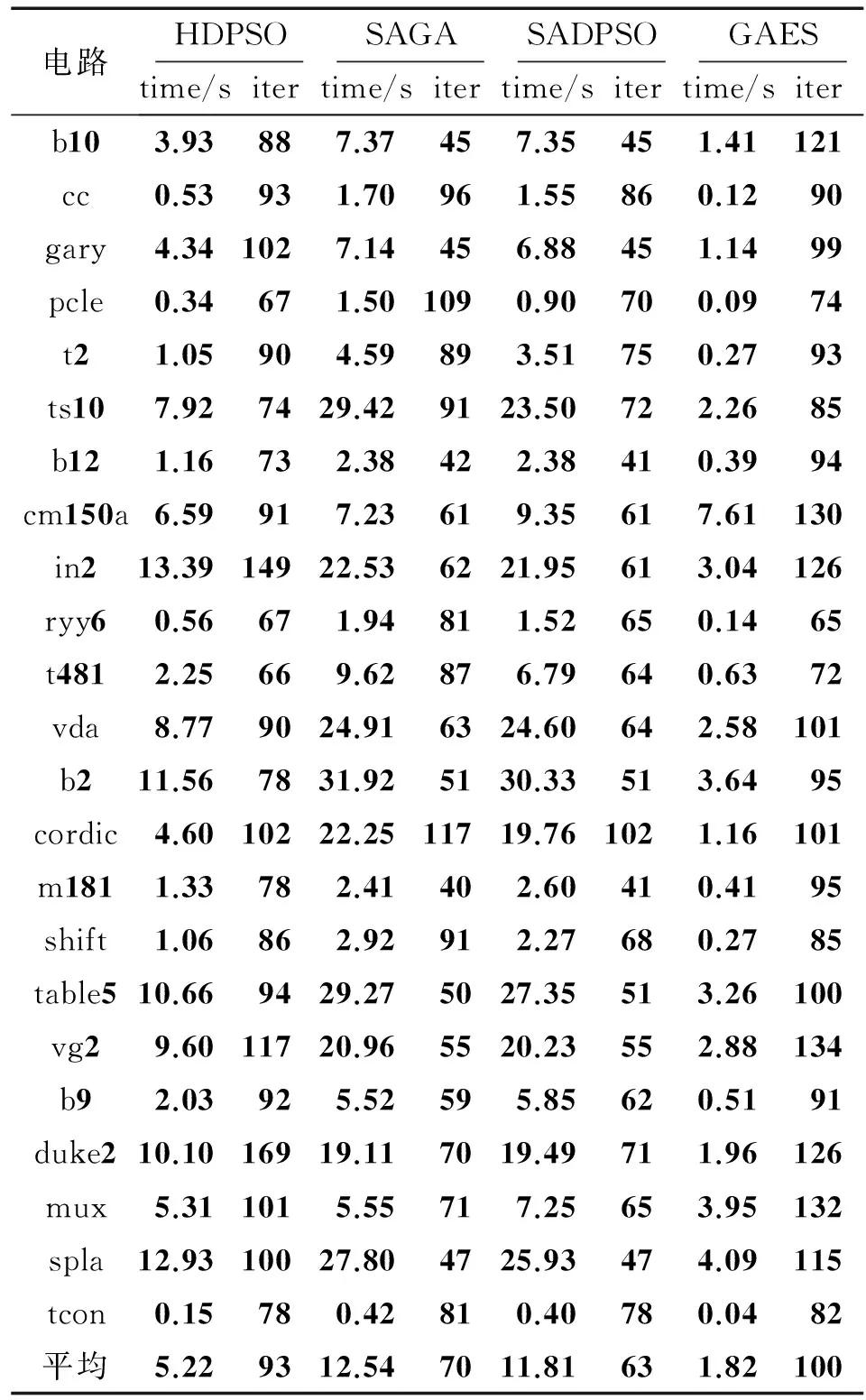
基于SADPSO的MPRM最小化算法

卜登立

(1. 井冈山大学 电子与信息工程学院，江西 吉安 343009；2. 同济大学 软件学院，上海 201804)



基于SADPSO的MPRM最小化算法

卜登立1,2

(1. 井冈山大学 电子与信息工程学院，江西 吉安 343009；2. 同济大学 软件学院，上海 201804)

摘要：针对混合极性Reed-Muller (mixed-polarity Reed-Muller, MPRM) 逻辑最小化问题，提出一种基于SADPSO (hybrid simulated annealing and discrete particle swarm optimization) 的智能算法。该算法将模拟退火 (simulated annealing, SA) 与离散粒子群优化 (discrete particle swarm optimization, DPSO) 相结合，对DPSO所得到的最佳解应用SA，帮助算法跳出局部极小。使用所提出算法和已有智能MPRM最小化算法分别对23个MCNC基准电路进行逻辑最小化，并对算法结果质量进行定量评价。结果表明，与已有智能MPRM最小化算法相比，所提出算法具有更好的全局收敛能力，能够提高算法结果质量。

关键词：混合极性Reed-Muller; 逻辑最小化; 智能算法; 模拟退火; 离散粒子群优化

0引言

Reed-Muller(RM)逻辑是布尔函数基于AND/XOR的表示，对于线性电路、通信系统和算术逻辑等电路而言，与基于AND/OR的布尔逻辑相比，RM逻辑可获得面积、功耗和可测性方面的优势[1-2]。混合极性RM(mixed-polarity Reed-Muller, MPRM)是一种RM标准形表示，相对于固定极性RM(fixed-polarity Reed-Muller, FPRM)，MPRM有可能获得更为简洁的表示，因此，MPRM的最小化问题得到了广泛的关注。

MPRM最小化是RM电路逻辑综合过程中一个非常重要的阶段，由于MPRM最小化问题属于NP难优化问题[2]，因此，对输入数较多的电路，研究者倾向于采用智能优化方法来完成MPRM最小化。在MPRM中，变量的极性属性有3种类型[1]，由于智能优化算法在进行编码选择时需要遵守完备性、健全性和非冗余性3个基本原则[3]，因此，对于MPRM最小化不宜使用类似于FPRM最小化时常采用的二进制编码[4]，而应使用三进制编码。因此，MPRM最小化问题属于多值离散优化问题[5]。

本文首先对当前的智能MPRM最小化算法进行概述，然后提出一种基于模拟退火离散粒子群优化(hybrid simulated annealing and discrete particle swarm optimization, SADPSO)的元启发式MPRM最小化算法，通过将模拟退火(simulated annealing, SA)与离散粒子群优化(discrete particle swarm optimization, DPSO)相结合，在每次迭代中使用SA对DPSO所搜索到的最佳解实施退火操作，增强算法的全局收敛能力。将之应用于输入数较多的电路，并与文献[1-2,5]中的算法进行了比较。

1智能MPRM最小化算法概述

1.1MPRM最小化

一个n个输入m个输出的多输出布尔函数，将n个变量按照一定顺序进行分解，可以得到如(1)式所示的MPRM标准形[1]。

(1)

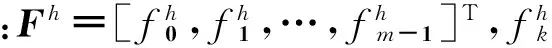
MPRM最小化通过对极性值进行选择以使得(1)式中的非零系数向量个数最少，即使MPRM表达式所包含的乘积项数最少。对于一个包含n个变量的完全确定布尔函数，其极性空间大小为3n，每个极性值可以确定一个如(1)式所示的MPRM。因此，MPRM最小化问题可以转化为求解最优极性值的问题，并描述为[2]

(2)

(2)式中，C(h)为成本函数，其值为极性值为h的MPRM表达式中所包含乘积项的个数。

1.2智能最小化算法概述

当前用于MPRM最小化的智能算法从算法主体角度可以分为基于遗传算法(geneticalgorithm,GA)的[1-2,6]和基于DPSO的[5, 7]两大类。

文献[6]将进化策略(evolutionarystrategy,ES)与GA相结合，采用(μ+1)-ES策略(μ为种群大小)，每次生成一个子个体，生成子个体时，采用锦标赛选择策略选择锦标赛规模内的最佳个体进行交叉；当种群再生时，采用锦标赛替换策略替换掉锦标赛规模内最差的个体。但是(μ+1)-ES策略有着降低变异强度的倾向，会对算法的性能产生非常大的影响[8]。文献[1]也将ES与GA相结合，但与文献[6]不同，其采用了(μ+λ)-ES策略，在种群进化时，每次生成λ(λ>1)个新个体。

对于输入数较多的电路，采用遗传算法可能由于过早收敛而无法得到全局最优解[2]，因此文献[2]给出了一种基于模拟退火遗传算法(simulated annealing genetic algorithm, SAGA) 的算法，通过在GA中加入模拟退火过程避免搜索陷入到局部极小，从而改善算法的结果，采用SAGA能够获得比GA更好的结果和性能[2]。

粒子群优化(particle swarm optimization, PSO)作为一种新的群智能优化算法，已被广泛地应用于各种复杂的优化领域[3,9-10]，近年来也被应用于MPRM最小化问题[5, 7]。文献[7]使用三进制编码，给出了一种用于MPRM最小化的DPSO算法，但是标准DPSO存在着多样性损失导致的过早收敛问题[5, 11]，尽管该算法在由连续域映射到三进制离散域的过程中引入了随机因素，但是文中并未对算法结果的质量进行定量评价。

文献[5]针对标准DPSO的过早收敛问题，提出了一种基于HDPSO(hybrid multi-valued DPSO)的算法，该算法采用多群策略，并在DPSO中引入了GA中的一些要素，如在粒子位置更新过程中引入概率变异策略及没有重复的更新策略来维持粒子的多样性，并加入了群间重复最佳变异策略来避免群间的碰撞，以使多个群尽可能搜索优化空间中不同的子空间，避免算法陷入局部极小，增强全局搜索能力。文献[5]使用基于列表技术的极性转换方法进行极性转换，将HDPSO在算法结果质量和时间效率方面与SAGA进行了对比，得出了HDPSO在时间效率上要优于SAGA的结论。

2SA结合DPSO的MPRM最小化算法

2.1MPRM极性转换

在MPRM最小化过程中需要进行MPRM极性转换，以得到不同形式的MPRM。基于OKFDD (ordered Kronecker functional decision diagram)的极性转换方法采用OKFDD表示电路，位于OKFDD中同一层变量的分解类型相同。如果将OKFDD中由根结点到值为1的叶结点且能够得到一个乘积项的路径称为有效1路径，那么遍历OKFDD中的有效1路径即可得到如(1)式所示的MPRM表达式[12]。对于多输出布尔函数，可以采用基于共享OKFDDs的极性转换方法[12]，共享OKFDDs在多个输出的OKFDD之间共享子图。使用共享OKFDDs表示MPRM，可通过统计共享OKFDDs中有效1路径的数量来统计MPRM表达式中乘积项的个数。

由于OKFDDs是简约表示[12]，与基于系数矩阵[1]和列表技术[2]的极性转换方法相比，基于共享OKFDDs的极性转换方法有可能得到更为紧凑的MPRM表示。因此，本文在进行MPRM最小化时采用基于共享OKFDDs的极性转换方法。

2.2编码和成本函数

由于MPRM中变量的极性属性为三进制表示，因此选择三进制编码[5]，并将极性向量作为粒子的位置向量Dj=[dj,n-1,…,dj,0]，dj,l表示粒子群中索引为j的粒子在n维搜索空间中第l维的位置，即MPRM第l个变量的极性属性。

所采用的成本函数为(2)式中的C(h)，在计算C(h)时，先根据极性向量对OKFDDs进行极性转换，然后再统计其中有效1路径的数量。

2.3SADPSO算法

DPSO算法是一种全局搜索算法，虽具有较快的收敛速度，但却存在着过早收敛问题[5, 11]。SA具有较强的局部搜索能力，通过引入随机搜索并在搜索过程中以一定概率接受恶化解，从而可以使搜索跳出局部极小[13-14]。

本文提出的SADPSO算法根据DPSO的快速收敛特点和SA较强局部搜索能力的特点，将SA与DPSO相结合，利用SA跳出局部极小，避免DPSO的过早收敛问题，以增强全局收敛能力。

2.3.1DPSO算法

假设粒子的速度向量用Vj=[vj,n-1,…,vj,0]表示，vj,l表示群中索引为j的粒子在n维搜索空间中第l维的速度，第j个粒子的个体历史最佳位置用Pj=[pj,n-1,…,pj,0]表示，粒子群的全局最佳位置用G=[gn-1,…,g0]表示，则粒子的速度更新公式为

(3)

(3)式中：W为惯性权重；C1和C2分别为认知和社会尺度参数；r1和r2是在[0,1]均匀分布的随机数；上标t表示第t次迭代。另外，速度限制参数Vmax可以改善搜索的分辨率[5]。

本文DPSO所采用的粒子位置更新公式为[5]

(4)

(4)式中，⎣y」为下取整函数。

算法1给出在SADPSO的一次迭代过程中的DPSO算法，其中N为粒子群规模。

算法1DPSO算法。

1)令j=0；

黔南州合作社大多设置较低的入社门槛并积极吸纳小农户社员，带动小农户的意愿较强。统计结果显示，42家合作社都在积极扩大社员规模，占总样本量的85.71%；不设置入社门槛的合作社为29家，占样本量的61.70%；仅有2家合作社设置最低种植规模门槛。值得注意的是，随着“村社合一”模式的大力推广，黔南州出现不少旨在带动全村农户，尤其是贫困户的“村社合一”型合作社，在带动小农户发展方面发挥了重要作用。这类合作社是由村干部领办组建，以村集体资产或扶贫项目资金帮助全村农户或贫困户入股，通过抱团发展产业带动全村农户发展。在49家样本合作社中有9家“村社合一”型合作社。

2)令l=0；

3)分别根据(3)式和(4)式更新vj,l和dj,l，并令l=l+1，如果l

4)令j=j+1，如果j

2.3.2SA算法

SA与有限长度马尔可夫链相对应，由一个初始状态开始，每一步状态的转移都是在当前状态Su的邻域N(Su)中随机产生新状态Sv，然后根据Metropolis准则接受新状态。状态转移概率如(5)式所示[13]。

(5)

(5)式中：ΔCuv=C(Su)-C(Sv)为成本函数差值；Tt为第t次迭代时的温度。

SA从初始温度T0开始，对每一温度Tt按(5)式所示转移概率进行随机搜索，直至平稳分布[13]，然后根据退温函数降温，直至达到冷冻状态[14]，此时得到的平稳分布即为所搜索到的最优解。

初始温度T0的选择会影响算法的结果和效率，本文通过n2[2]次随机变换，使用成本函数的平均增量确定初始温度[14]。假设初始接受概率为pa，则初始温度可由(6)式计算。

(6)

退温函数采用如(7)式所示的指数冷却调度方案[2, 15]。

(7)

算法2给出在SADPSO算法的一次迭代过程中的SA算法，其中，OD为DPSO所得到的最佳解，L=N×n[2]为马尔可夫链的最大长度。状态Su由极性向量Du表示，其邻域N(Su)由与Du格雷码距为1的极性向量构成。

算法2SA算法。

1)将OD作为SA的初始状态S0，计算C(S0)；令b=0，u=0；

2)从状态Su的邻域N(Su)随机产生新状态Sv，计算C(Sv)和ΔCuv，并按(5)式所示的概率接受新状态Sv，如果Sv不被接受，则转步骤3)，否则令u=u+1，Su=Sv；如果u

3)令b=b+1，如果b

4)将上述过程得到的最优解OS与OD进行竞争，如果OS的成本小于OD的成本，则使用OS替换OD，并更新OD的历史最佳信息。

2.3.3算法结束条件

本文从两方面来考虑SADPSO算法的结束条件。如果DPSO的寻优结果没有改变所累计的次数达到20×ln(n)[5]则结束算法。随着温度的衰减，SA接受恶化解的概率逐渐减小，SA将收敛于最优解。因此，如果在一次模拟退火过程中，没有被接受新状态的比例达到50%则结束算法[2]。

2.3.4SADPSO算法描述

下面给出DPSO和SA结合并用于MPRM最小化的SADPSO算法。

算法3SADPSO算法。

1)初始化DPSO和SA相关参数；

2)读取逻辑网表并转换为OKFDDs；

4)生成初始粒子群，计算群中粒子的成本，并更新粒子的个体历史最佳及全局最佳；

5)迭代次数初始化为0；

6)运行算法2，如果新状态Sv没有被接受的比例达到50%，则转步骤8)，否则采用(7)式进行退温操作，并转步骤7)；

7)运行算法1，迭代次数+1，计算群中粒子的成本，并更新粒子个体历史最佳以及全局最佳，统计群最佳没有改变所累计的次数，如果该次数等于20×ln(n)或迭代次数达到最大迭代次数则转步骤8)，否则转步骤6)；

8)输出最优MPRM结果，算法结束。

算法3的第4)和7)步，在计算群中粒子的成本函数值时，采用文献[1]中基于最短个体距离的成本函数计算方法。

SADPSO利用SA对DPSO所搜索到的全局最佳解实施模拟退火操作，在DPSO进行全局探索的同时，SA进行局部精搜以改善DPSO的搜索效率[15]，从而增强全局收敛能力。由于SA能够实现较好的局部精搜，因此DPSO应该着力于全局探索，在参数设置时，可通过设置较大的W值来实现这个目的。

3实验设置及结果分析

为进行验证和分析，将本文的SADPSO算法与文献[1]中的GAES、文献[2]中的SAGA算法以及文献[5]中的HDPSO算法进行比较。4种算法均采用基于共享OKFDDs的MPRM极性转换方法，以及(2)式的成本函数和优化目标，并用C++实现，在Linux下使用g++编译器编译。使4种算法分别对一组输入数大于14的MCNC基准电路在配置为IntelCorei3-2350MCPU6GBRAM的个人计算机上进行MPRM最小化。

3.1实验设置

SADPSO中的DPSO的参数设定为N=30，W=1.2，C1=C2=2，Vmax=4，SA的参数设定与文献[2]相同。HDPSO算法的参数与文献[5]相同。SAGA中GA的种群规模设定为30，SAGA除了根据接受概率设置结束条件外，如果GA的寻优结果没有改变的累计次数达到20×ln(n)也将结束SAGA。GAES的种群规模也为30，由于本文是对输入数较多的电路进行MPRM最小化，因此选择次数参数设为8，如果在达到最大迭代次数之前，寻优结果没有改变累计次数达到20×ln(n)也将结束GAES，其他参数与文献[1]相同。4种算法的最大迭代次数均设定为180。

由于4种算法均具有一定的随机特性，因此实验中对于每个基准电路，每种算法均独立运行20次，并统计运行结果的最小值、均值和标准差，以及算法迭代次数和所花费CPU时间的平均值。

3.2结果分析

表1给出了4种算法的运行结果，其中“I/O”表示电路的输入数和输出数，min，avg和std分别表示算法20次独立运行所得到的最优MPRM所包含乘积项数的最小值、均值及标准差。

从表1中算法多次独立运行的结果可以看出，GAES对于很多电路均不能稳定地得到MPRM最小结果，特别是对于电路ts10，算法结果的均值和标准差均比较大，算法不能很好地收敛于全局最优解。可见，对于输入数较多的电路，GAES不能很好地解决过早收敛的问题。

对于SADPSO，HDPSO和SAGA，3种算法能够得到基本类似的结果，除电路ts10和mux外，3种算法结果的最小值都相同，均值也基本相同，均值都等于或者非常接近最小值，并且对于某些电路而言，这3种算法均能稳定地获得最小MPRM结果，对其余电路而言，标准差也都比较小。对于能够稳定地得到最小MPRM结果的电路，SADPSO共有19个，比例达到82.61%，HDPSO共有11个(不包括ts10和mux)，比例为47.83%，SAGA共有14个，比例为60.87%。对于电路ts10和mux，尽管20次独立运行HDPSO都能够得到乘积项数分别为136和17的结果，但该结果并不是最小结果，而SADPSO与SAGA尽管不能稳定地获得最小结果，但是却具备搜索到最小结果的能力。从多次独立运行能够稳定获得最小解的比例来看，SADPSO最高，这表明SADPSO具有非常强的全局收敛能力。

为进一步比较，图1给出了3种算法结果的变异系数[5](其中，不包括3种算法变异系数均为0的结果)，变异系数可用来衡量不同均值时数据的稳定性。由图1可以看出，SADPSO具有最好的结果稳定性，HDPSO次之，SAGA由于存在着较高的尖峰(cm150a)，稳定性相对较差。

表2给出了4种算法分别20次独立对基准电路进行MPRM最小化所花费的CPU时间(time)和算法迭代次数(iter)的平均值，时间的单位为秒。

由表2中的平均结果可以看出，从算法时间效率上来看，尽管GAES所用的迭代次数最多，但时间效率最高，这是因为GAES每次迭代过程仅生成少量的新个体，计算新个体适应度所花费的时间较少。尽管时间效率较高，但是对于某些电路，如ts10，由于算法容易陷入局部极小而导致过早收敛，牺牲了算法结果的质量。

对于算法SADPSO，HDPSO和SAGA，从时间效率角度来看，HDPSO最优，SADPSO与SAGA时间效率相对较低，但是SADPSO略优于SAGA。从迭代次数角度来看，SADPSO最少，SAGA次之，HDPSO所需迭代次数最多。虽然对于大部分电路而言，SADPSO与SAGA算法迭代次数均比HDPSO少，但是由于SADPSO和SAGA算法在迭代过程中加入了较为耗时的模拟退火操作，每次迭代过程所花费的时间要比 HDPSO 长。另外，SA确定初始温度的过程也使算法所花费的时间有所增加。尽管SADPSO采用了与SAGA类似的模拟退火过程以及相同的SA参数，但SADPSO算法所需迭代次数以及所花费的时间要低于SAGA，这说明了DPSO比GA具有更快的收敛速度。

综上所述，从总体角度来看，与SAGA相比，SADPSO具有较高的稳定性和较高的时间效率，SADPSO能够稳定获得最小解电路的个数是SAGA的1.36倍，算法时间效率相对SAGA提高了5.82%。和HDPSO相比，虽然算法时间是HDPSO的2.26倍，但SADPSO具有非常高的稳定性，SADPSO能够稳定获得最小解电路的个数是HDPSO的1.73倍。由于SADPSO具有非常强的全局收敛能力，因此SADPSO也是MPRM最小化一个较好的选择。

表2　4种算法的迭代次数以及时间

4结束语

由于MPRM存在着指数级大小的极性空间，对于输入数较多的电路，想要在合理时间内得到最小MPRM，经常采用智能优化方法。本文对当前的智能MPRM最小化算法作了概述，并提出一种基于SADPSO的MPRM最小化算法，该算法将DPSO和SA相结合，使用SA对DPSO所得到的最佳解实施模拟退火操作。实验结果验证了所提出算法的有效性，DPSO与SA能够很好地进行互补，DPSO进行全局探索，SA则进行局部精搜，避免了标准DPSO存在的过早收敛问题，增强了全局收敛能力。与HDPSO相比，SADPSO具有更高的结果质量，和SAGA相比，SADPSO具有较高的结果质量和较高的时间效率。

参考文献：

[1]卜登立, 江建慧. 使用系数矩阵变换极性转换的MPRM电路面积优化[J]. 计算机辅助设计与图形学学报, 2013, 25(1): 126-135.

BU Dengli, JIANG Jianhui. Area optimization of MPRM circuits utilizing coefficient matrix transformation based polarity conversion[J]. Journal of Computer-Aided Design & Computer Graphics, 2013, 25(1): 126-135.

[2]WANG P, LI H, WANG Z. MPRM expressions minimization based on simulated annealing genetic algorithm [C]//IEEE. Proceedings of the 2010 International Conference on Intelligent Systems and Knowledge Engineering. New York, USA: IEEE Press, 2010: 261-265.

[3]郭文忠, 陈国龙, XIONG Naixue, 等. 求解VLSI电路划分问题的混合粒子群优化算法[J]. 软件学报, 2011, 22(5): 833-842.

GUO Wenzhong, CHEN Guolong, XIONG Naixue, et al. Hybrid particle swarm optimization algorithm for VLSI circuit partitioning[J]. Journal of Software, 2011, 22(5): 833-842.

[4]ZHANG H, WANG P, GU X. Area optimization of fixed-polarity Reed-Muller circuits based on niche genetic algorithm[J]. Chinese Journal of Electronics, 2011, 20(1): 27-30.

[5]卜登立, 江建慧. 基于混合多值离散粒子群优化的混合极性Reed-Muller最小化算法[J]. 电子与信息学报, 2013, 35(2): 361-367.

BU Dengli, JIANG Jianhui. Hybrid multi-valued discrete particle swarm optimization algorithm for mixed-polarity Reed-Muller minimization[J]. Journal of Electronics & Information Technology, 2013, 35(2): 361-367.

[6]AL-JASSANI B A, URQUHART N, ALMAINI A E A. Manipulation and optimisation techniques for Boolean logic[J]. IET Computers and Digital Techniques, 2010, 4(3): 227-239.

[7]YU H, WANG P, WANG D, et al. Discrete ternary particle swarm optimization for area optimization of MPRM circuits[J]. Journal of Semiconductors, 2013, 34(2): 118-123.

[8]BEYER H G, SCHWEFEL H P. Evolution strategies: a comprehensive introduction[J]. Natural Computing, 2002, 1(1): 3-52.

[9]BANKS A, VINCENT J, ANYAKOHA C. A review of particle swarm optimization. Part I: background and development[J]. Natural Computing, 2007, 6(4): 467-484.

[10] 周相兵. 一种基于粒子群优化的虚拟资源分配方法[J]. 重庆邮电大学学报: 自然科学版, 2014, 26(5): 686-693.

ZHOU Xiangbing. An optimization approach of virtual resources allocation based on particle swarm algorithm[J]. Journal of Chongqing University of Post and Telecommunications: Natural Science Edition, 2014, 26(5): 686-693.

[11] BLACKWELL T, BRANKE J. Multi-swarm optimization in dynamic environments[J]. Lecture Notes in Computer Science, 2004, 3005: 489-500.

[12] DRECHSLER R, BECKER B. Ordered Kronecker functional decision diagrams-a data structure for representation and manipulation of Boolean functions[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 1998, 17(10): 965-973.

[13] GLOVER F, KOCHENBERGER G A. Handbook of metaheuristics[M]. New York: Springer, 2003: 287-319.

[14] KOUVELIS P, CHIANG W C. A simulated annealing procedure for single row layout problems in flexible manufacturing systems[J]. International Journal of Production Research, 1992, 30(4): 717-732.

[15] LV H, LU C, ZHA J. A hybrid DPSO-SA approach to assembly sequence planning [C]// IEEE. Proceedings of the 2010 International Conference on Mechatronics and Automation. New York, USA: IEEE Press, 2010: 1998-2003.

MPRM minimization algorithm based on SADPSO

BU Dengli1,2

(1. School of Electronics and Information Engineering, Jinggangshan University, Ji’an 343009, P. R. China;2. School of Software Engineering, Tongji University, Shanghai 201804, P. R. China)

Abstract:A hybrid simulated annealing and discrete particle swarm optimization (SADPSO) based intelligent algorithm is proposed for mixed-polarity Reed-Muller (MPRM) logic minimization. The proposed algorithm combines simulated annealing (SA) and discrete particle swarm optimization (DPSO) by applying SA to the best solution obtained by DPSO to help the algorithm escape from local minima. Twenty-three MCNC benchmark circuits are minimized respectively by using the proposed algorithm and existing intelligent MPRM minimization algorithms, and the qualities of algorithm results are evaluated quantitatively for these algorithms. The results show that, compared to existing intelligent MPRM minimization algorithms, the proposed algorithm has better ability of global convergence, and can improve the qualities of algorithm results.

Keywords：mixed-polarity Reed-Muller; logic minimization; intelligent algorithm; simulated annealing; discrete particle swarm optimization

DOI：10.3979/j.issn.1673-825X.2016.02.014

收稿日期：2015-05-11

修订日期：2015-07-08通讯作者：卜登立bodengli@163.com

基金项目：江西省自然科学基金(20122BAB201038)；江西省教育厅科技计划项目(GJJ13538)

Foundation Items：The Natural Science Foundation of Jiangxi Province(20122BAB201038); The Science and Technology Project of the Education Department of Jiangxi Province(GJJ13538)

中图分类号：TP331.2; TP391.72

文献标志码：A

文章编号：1673-825X(2016)02-0226-07

作者简介：

卜登立(1975-)，男，河北定州人，副教授，博士，主要研究方向为VLSI设计和可靠性评估、智能优化算法、计算机辅助设计。E-mail：bodengli@163.com。

(编辑：魏琴芳)