基于信息熵改进的K-means动态聚类算法

杨玉梅

(川北医学院 图书馆,四川 南充 637000)



基于信息熵改进的K-means动态聚类算法

杨玉梅

(川北医学院 图书馆,四川 南充 637000)

摘要：初始聚类中心及聚类过程产生的冗余信息是影响K-means算法聚类性能的主要因素，也是阻碍该算法性能提升的主要问题。因此，提出一个改进的K-means算法。改进算法通过采用信息熵对聚类对象进行赋权来修正聚类对象间的距离函数，并利用初始聚类的赋权函数选出质量较高的初始聚类中心点；然后，为算法的终止条件设定标准阈值来减少算法迭代次数，从而减少学习时间；最后，通过删除由信息动态变化而产生的冗余信息来减少动态聚类过程中的干扰，以使算法达到更准确更高效的聚类效果。实验结果表明，当数据样本数量较多时，相比于传统的K-means算法和其他改进的K-means算法，提出的算法在准确率和执行效率上都有较大提升。

关键词：K-means算法；信息熵；数据挖掘；动态聚类

0引言

聚类分析作为数据挖掘的重要分支，在信息化时代起着举足轻重的作用。聚类分析的目标在于将数据集分成若干个簇，并保证同一簇内的数据点相似度尽可能的大，簇与簇之间的数据点的相似度尽可能的小[1]。聚类操作是对事先未知的数据对象进行类的划分，而类的形成是由数据驱动来完成。在数据挖掘领域中，聚类分析既可以作为数据挖掘过程中的一个环节，又可以作为获取数据分布情况的工具。聚类分析的应用前景较为广泛，比如：生物种群的划分、目标客户的定位、市场趋势分析、模式识别及图像处理等[2]。

K-means算法是聚类分析常用的方法之一，该算法的特点在于简单、效率高且宜于处理大规模的数据，已经被应用到众多领域，如自然语言处理、天文、海洋、土壤数据处理等[3]。自K-means算法提出以来，大量有关K-means算法的研究如雨后春笋般涌现，同时该算法的弊端也纷纷暴露出来，主要包括以下4点：①必须事先确定K值。②聚类结果会受到初始聚类中心影响。③处理分类属性数据较为困难且易产生局部最优解[4]。④当数据样本数量较大时，不仅使算法的时间开销非常大，且由聚类的动态变化导致的冗余信息也将对算法产生影响。由于上述K-means算法的第1和第3个缺点是算法本质所致，几乎是无法改变的，为此，国内外诸多专家学者针对其余不足提出了众多解决方法。文献[2]提出基于密度的改进K均值算法，该算法针对由初始中心点的随机产生导致的聚类结果的不稳定提出了改进算法；文献[3] 提出基于密度和最邻近的K-means文本聚类算法；文献[4]提出聚类模式下一种优化的K-means文本特征选择算法，文献[5]提出基于信息熵的精确属性赋权K-means聚类算法,文献[6]提出一种基于余弦值和K-means的植物叶片识别方法等。然而，国内外诸多专家学者在一定程度上都是对K-means算法的初始聚类中心进行优化，并没有考虑数据样本数量较多的情况。

在上述情况下，论文针对K-means算法的第2点和第4点不足，提出基于信息熵的K-means动态聚类方法，该算法首先通过熵值法对聚类对象赋权的方式来修正对象间的距离函数，利用初始聚类的赋权函数值选出质量较高的初始聚类中心点。其次通过为算法的终止条件设定标准值，减少算法迭代次数，减少学习时间；通过删除由信息动态变化而产生的冗余信息，减少动态聚类过程中的干扰，使算法达到更准确更高效的聚类效果。

1相关基本定义

假设Α={ai|ai∈Rm,i=1,2,…,n}为给定的数据集，Ti(i=1,2,…,k)代表第i个类别，c(T1),c(T2),…,c(Tk)分别是k个聚类中心。有如下定义。

定义1设向量ai=(ai1,ai2,…,aim)和向量aj=(aj1,aj2,…,ajm)分别代表2个数据对象，那么它们之间的欧式距离定义为

(1)

定义2同一类别的数据对象的质心点定义为

(2)

(2)式中，|Ti|是Ti中数据对象的个数。

定义3同属于Tj组的ni个数据对象ai(i=1,2,…,n1)的标准差[5]σ定义为

(3)

2优化K-means算法的初始聚类中心点

传统的K-means算法是随机选择初始聚类中心点，可能造成在同一类别的样本被强行当做2个类别的初始聚类中心点，使结果簇只能收敛于局部最优解，因此，为了选出更为合理的初始聚类中心，需要对初始聚类中心进行预处理，基本思想[6]为：首先把数据集平均分成k1(k1>k)个子集，在每个子集中随机选出某一数据对象，然后把这k1个数据对象当做聚类种子中心进行初聚类，计算每个类别的赋权类别价值函数σi，按照从小到大的顺序进行排列，最后把前k个类对应的质心作为初始聚类的中心点。

(4)

使用熵值法[7]确定属性权重值的步骤如下：

Step 1构造属性值矩阵

其中，n表示样本数据个数，m为每个数据对象的维数。

Step 2计算第j维属性对应的第i个数据对象的属性值比重。需要对数据进行标准化处理，即将数据压缩到区间[0,1]，其过程如(5)式所示

(5)

(5)式中：Mij表示属性值比重，xij代表属性值，i=1,2,…,n，j=1,2,…,m。

Step 3计算第j维属性的熵值

(6)

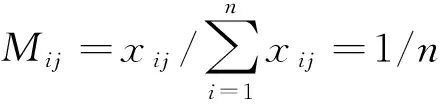
Step 4计算第j维属性的差异性系数为

(7)

对于给定的j，当Hj越小时，qj越大，属性越重要。

Step 5第j维的属性权值的计算

(8)

Step 6使用欧式距离计算数据对象之间的相似性，根据定义1可得赋权后的欧式距离[8]为

(9)

(9)式中，ωj是第j维属性的权值。相当于使权值对应的属性值进行了适当的放大或缩小，使权值大的属性聚类作用更大，权值小的属性聚类作用更小。

Step 7采用标准差作为标准测度函数，由定义3求得赋权类别目标价值函数[9]为

(10)

(10)式中：σi表示第i类的赋权标准差；|Tj|是Tj所含数据对象的个数。由(10)式可知，σi的值越小，类内数据对象相似度越大，数据对象越密集，其所在类的质心越能够体现分类决策面。

3本文改进算法

3.1K-means算法改进思想

在样本数据聚类的过程中，不仅需要计算每个聚类对象与他们中心对象的距离，还需要重新计算中心对象发生变化的聚类的均值，且计算是在一次次迭代中重复完成，当数据样本较多时，过大的计算量会严重影响算法的性能。其次，由于K-means聚类是个动态变化的过程，聚类过程中将产生一些冗余信息，会对聚类产生一些不必要的干扰。针对K-means算法的以上缺陷，提出2点优化原则。①减少聚类过程中的迭代次数；②减少聚类过程中的数据量。K-means动态聚类算法的基本思想：由于K-means算法是通过迭代的过程把数据集划分为不同的类别，首先为中心点的该变量设定一个值，在迭代的过程中，当中心点的该变量小于某个设定值时，将整个簇加入到已选数据集，同时将它从样本集中删除，使得原始样本数据集中只保留未被正确识别的样本。然后算法进入下一轮循环，对其他样本进行筛选，直到所有样本数据都被正确识别。

3.2本文改进算法描述

结合基于信息熵的赋权方法与K-means的动态聚类对数据集合进行聚类处理，算法流程如图1所示。

算法步骤描述如下

输入：数据对象集A，聚类种子初始中心点个数k1。

输出：k个结果簇，使每个聚类中心点的改变量小于设定的值，直至数据对象集合为∅。

Step 2使用熵值法计算数据对象各个属性的权值。

Step 3将数据集平均分成k1(k1>k)个子集，从各个子集中随机选出一个数据对象，并将其作为聚类种子中心。

Step 4扫描数据集合，根据其与各聚类种子中心的相似度(赋权后的欧式距离)，将其归于与其最相似的簇中。

Step 5计算k1个聚类的σi(i=1,2,…,k1)，并按照σi值递增顺序排序，选前k个σi值对对应的质心作为初始聚类中心。

Step 6将样本集中的样本按照欧式距离最短原则分配到最邻近的簇中。

Step 7计算每个类的质心点。

Step 8判断聚类中心点的改变量是否满足设定的条件，如果满足，将其加入到已选特征集，同时将它从数据样本集中删除。

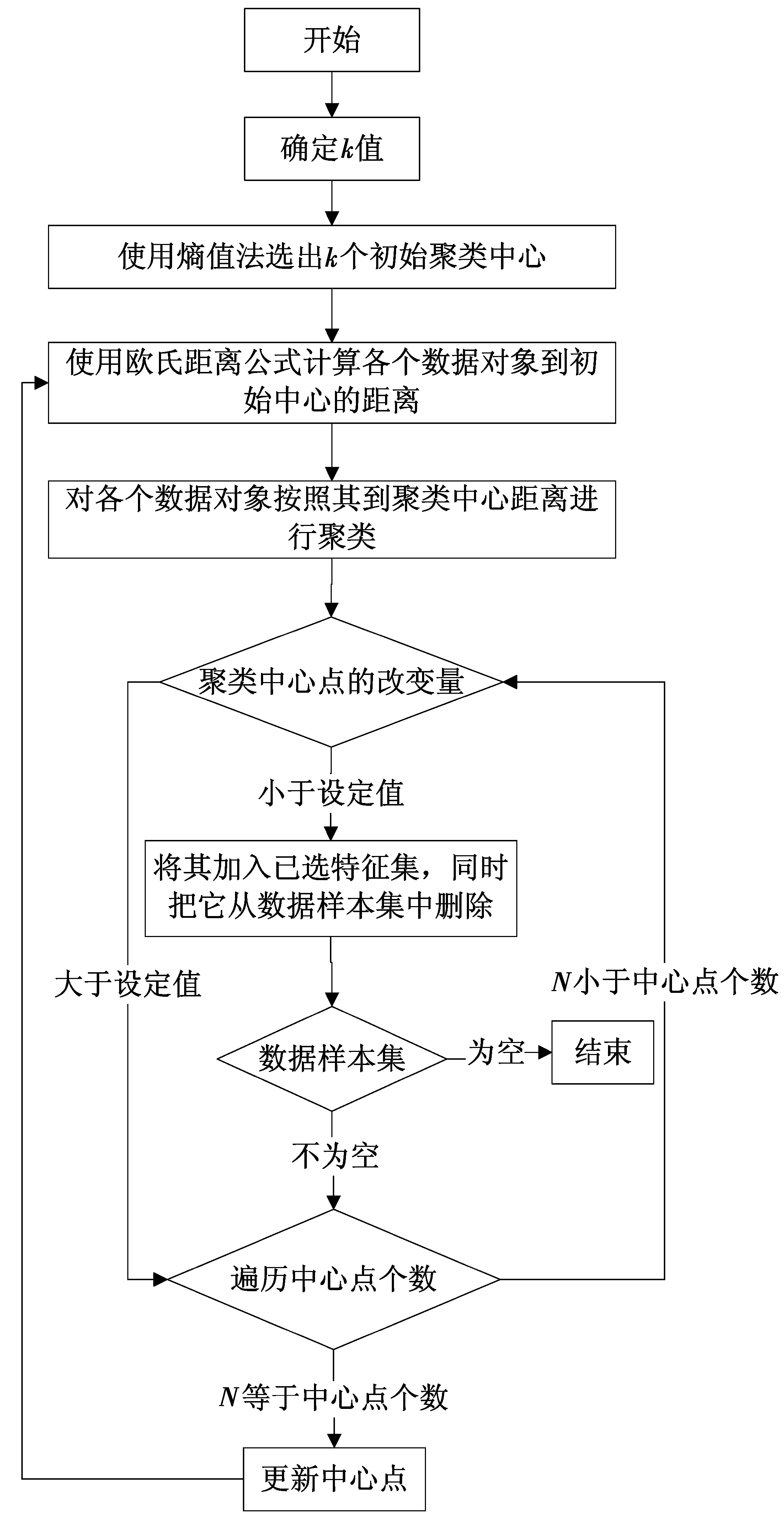
图1　本文改进算法流程图Fig.1　Flow chart of the proposed improved algorithm

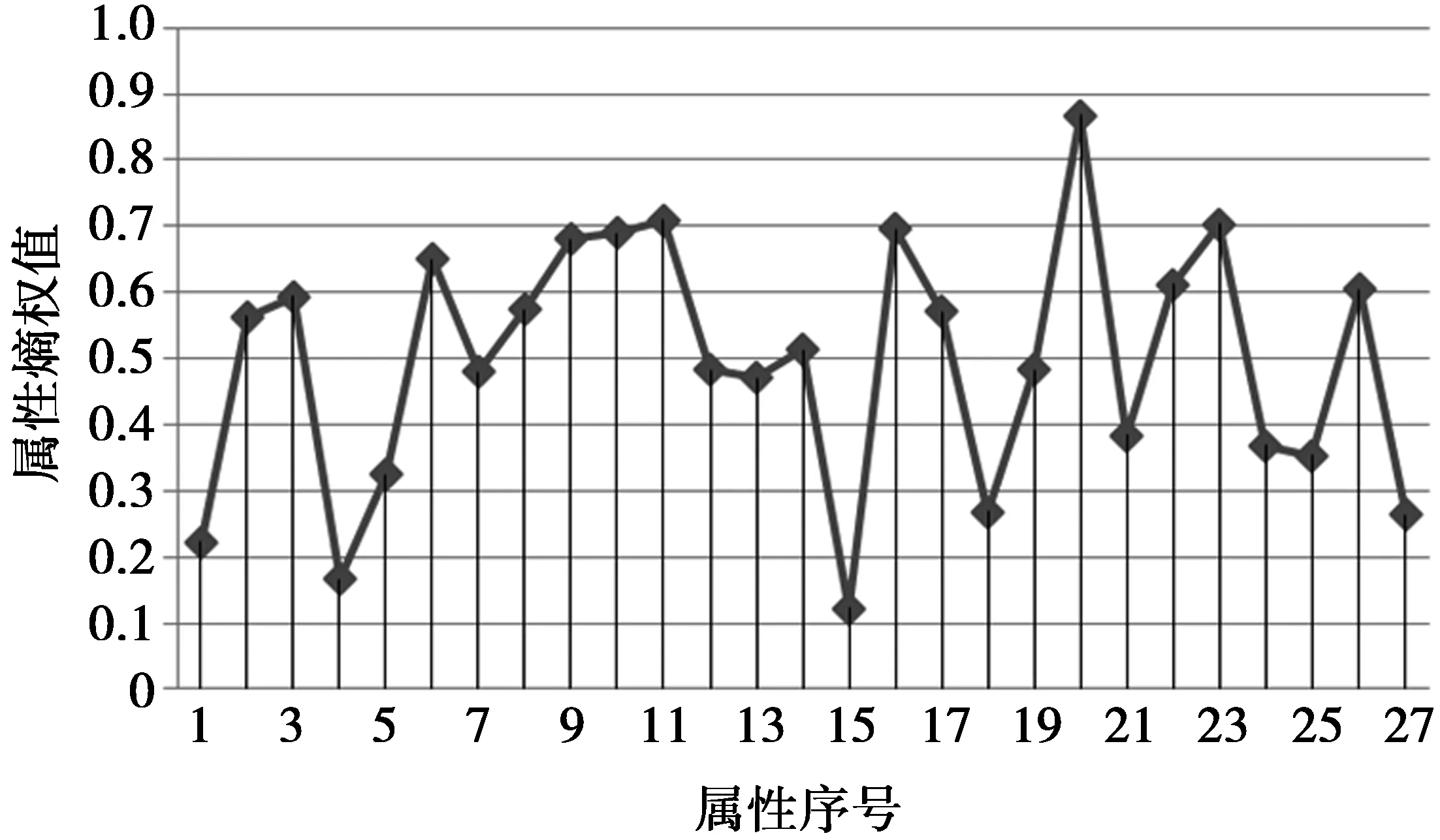
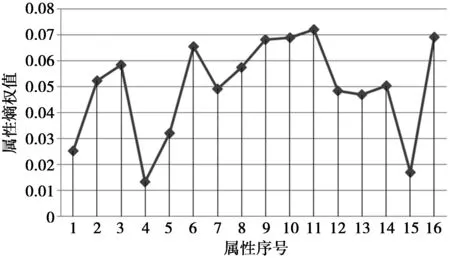
Step 9判断数据样本集是否为空，如果为空，结束算法。如果不为空，遍历中心点个数N，当N

Step 10更新中心点。计算每个聚类中心点的改变量大于设定值的簇的质心，并将其作为新的聚类中心，然后转向Step 6。

Step 11结束，数据样本为空集，得到k个结果簇。

算法优点：该算法不但利用熵值法提升了所选初始中心的质量，而且还通过为算法终止条件设定标准值以及删除由信息动态变化而产生的冗余信息的策略，减少了算法学习时间及干扰，从而使算法较高效地获得高质量的聚类效果。

4对比实验

4.1实验数据集

为了分析本文改进算法的聚类性能，使用5种不同的公用数据集合进行模拟实验。数据样本集合均来自UCI机器学习数据库，UCI数据库是一个专门用于数据挖掘算法和测试机器学习的公用数据库。库中的数据均有确定的属性类别，因此，可以用准确率和时间效率来衡量聚类性能的优劣。为验证传统K-means算法和本文改进算法的准确率和时间效率，不对测试数据集的数据分布做任何人为处理。表1描述了5组数据的概要信息，如名称，样本数和类别数等。

表1　实验数据集

从表1可以看出，5组数据分别由不同的数量样本数和类别数组成，数据集的多元性在一定程度上验证了它们在不同条件下的性能，保证了实验结果具有普遍性。

4.2实验结果对比

1)计算得到Lung-cancer数据集各属性对应的权值如图2所示，Promoter数据集各属性对应的权值如图3所示。

图2　Lung-cancer属性熵权值Fig.2　Lung-cancer entropy property values

由图2和图3中的属性熵权重数据得知，每个属性的聚类作用不同，应该对其加以区分，传统的K-means算法忽略了属性对聚类作用的差异度，致使数据对象的误判情况频繁出现，真实聚类结果与算法的聚类结果之间有一定的差距。

图3　Promoter属性熵权值Fig.3　Promoter entropy property values

2)为了尽可能地避免K-means算法本身固有的缺陷对实验结果造成影响，现对实验数据做如下预处理：

由图4可见，本文改进算法对数据样本数量较多的Coil2000和Isolet数据集取得了较高的聚类精度，说明改进后的算法对Coil2000和Isolet数据集有较好的聚类效果。对数据样本数量较小的Lung-cancer和Promoter数据集，本文改进算法精度低于传统K-means算法和文献[12]的K-means算法，说明当数据样本数量较小时，改进后的算法并不可取。由图5可见，传统的K-means算法和文献[12]的K-means算法较改进后的算法在执行时消耗的时间要多，改进后的算法在执行效率上较传统算法有较大的提升，并且数据样本数量越大，算法执行效率就越高。

图4　3种K-means算法精度对比结果Fig.4　Accuracy comparison results of threeK-means algorithms

图5　3种K-means算法执行时间对比结果Fig.5　Execution time comparison results of three K-means algorithms

经分析可知，造成上述实验结果的原因如下：本文改进算法不仅优化了初始聚类中心，而且还对学习迭代条件进行优化，同时还删除了由信息动态变化而产生的冗余信息从而减少动态聚类过程中的干扰；文献[12]中的K-means算法仅对初始聚类中心进行了优化，传统经典K-means算法并没做任何改变。这使得本文改进算法在聚类耗时上优于其余2种作对比的K-means算法。然而，由于本文改进算法在聚类过程中删除了一些动态信息，这在样本数量较少的情况下将损失占比较大的有用信息，聚类精度也就较低，甚至低于传统K-means算法。但是，在样本数量较多的情况下损失的一些有用信息占的比例就十分小， 甚至损失可以忽略不计，此时本文改进算法优势就显现出来了，聚类精度超过了文献[12]的K-means算法。

5结束语

K-means算法是一种应用广泛的聚类算法，在众多领域都取得了较好的聚类效果，本文针对初始中心点的问题和聚类过程中产生冗余信息的问题，提出了一种基于信息熵改进的K-means动态聚类算法，新算法不仅在选取初始中心点方面有明显的优势，而且简化了算法的复杂度，提高了聚类的精度。虽然如此，算法固有的缺陷依然对聚类的性能造成了一定的影响，如K-means算法需要事先确定k的个数；对孤立点数据很敏感等[11]；目前已有不少学者针对这些问题进行研究。这也是作者下一步要研究的问题。

参考文献：

[1]袁利永,王基一. 一种改进的半监督K-Means聚类算法[J].计算机工程与科学,2011,33(6):138-143.

YUAN Liyong,WANG Jiyi. An Improved Semi-Supervised K-Means Clustering Algorithm[J]. Computer Engineering and Science, 2011,33(6):138-143.

[2]傅德胜,周辰.基于密度的改进K均值算法及实现[J].计算机应用,2011,31(2):432-434.

FU Desheng,ZHOU Chen. Improved K-means algorithm and its implementation based on density[J]. Journal of Computer Applications, 2011,31(2):432-434.

[3]张文明,吴江,袁小蛟.基于密度和最邻近的K—means文本聚类算法[J].计算机应用,2010,30(7):1933-1935.

ZHANG Wenming,WU Jiang,YUAN Xiaojiao. K-means text clustering algorithm based on density and nearest neighbor[J]. Journal of Computer Applications, 2010,30(7):1933-1935.

[4]刘海峰,刘守生,张学仁.聚类模式下一种优化的K-means文本特征选择[J].计算机科学,2011,38(1):195-197.

LIU Haifeng,LIU Shousheng,ZHANG Xueren.Clustering-based Improved K-means Text Feature Selection[J]. Computer Science, 2011,38(1):195-197.

[5]朱颢东,申圳.基于余弦值和K-means的植物叶片识别方法[J].华中师范大学学报(自然科学版),2014,48(5):650-655.

ZHU Haodong,SHEN Zhen. Plant Leaf Identification Method Based on Cosine Theorem and K-means[J].

Journal of central China normal university (natural science edition), 2014,48(5):650-655.

[6]LEE S S, LIN Jachen.An accelerated K-means clustering algorithm selction and erasure rules[J]. Zhejiang University-SCIENCE C(Computers Electronics), 2012,13(10): 761-768.

[7]原福永,张小彩,罗思标.基于信息熵的精确属性赋权K-means聚类算法[J].计算机应用,2011,31(6)1675-1677.

YUAN Fuyong.,ZHANG Xiaocai,LUO Sibiao. Accurate property weighted K-means clustering algorithm based oninformation entropy[J]. Journal of Computer Applications, 2011,31(6)1675-1677.

[8]ORAKOGLU F E, Cevdet Emin Ekinci. Optimization of constitutive parameters of foundation soils K-means clustering analysis[J]. Sciences in Cold and Arid Regions, 2013, 5(5) :0626-0636.

[9]TABAKHI S. An unsupervised feature selection algorithm based on ant colony optimization[J].Engineering Applications of Artificial intelligence, 2014,32: 112-123.

[10] DERNONCOURT, DAVID. Analysis of feature selection stability on high dimension and small sample data[J].Computational Statistics and Data Analysis, 2014,71:681-693.

[11] 吴志媛,钱雪忠.基于PLSI的标签聚类研究[J].计算机应用研究,2013,30(5):1316-1319.

WU Zhiyuan,QIAN Xuezhong. Tag clustering research based on PLSI[J]. Application Research of Computers, 2013,30(5):1316-1319.

[12] REHAB D, MOHAMMED A R. A novel approach for initializing the spherical K-means clustering algorithm [J]. Simulation Modeling Practice and Theory,2015, 54(5):49-63.

Improved K-means dynamic clustering algorithm based on information entropy

YANG Yumei

(Library of North Sichuan Medical College, Nanchong 637000, P.R. China)

Abstract:Initial cluster centers and redundant information which is generated in clustering process will affect the clustering performance of K-means algorithm. In order to overcome the above mentioned shortcomings, a modified K-means algorithm is proposed. Firstly, it uses information entropy empowering the clustering objects to correct the distance function, and then employs empowerment function to select the optimal initial cluster centers. Subsequently, it decreases algorithm iterations to reduce learning time by setting the threshold value for termination condition of the algorithm.Finally,it reduces interference of dynamic clustering by removing redundant information from clustering process to make the proposed algorithm achieve more accurate and efficient clustering effect. The experimental results show that, when the data sample is larger, compared with the traditional K-means algorithm and other improved K-means algorithm, this improved K-means algorithm has large improvement in accuracy and efficiency.

Keywords：K-means algorithm; information entropy; data mining; dynamic clustering

DOI：10.3979/j.issn.1673-825X.2016.02.018

收稿日期：2015-04-11

修订日期：2015-12-10通讯作者：杨玉梅yangyumei7810@163.com

中图分类号：TP301

文献标志码：A

文章编号：1673-825X(2016)02-0254-06

作者简介：

杨玉梅(1978-),女, 四川南充人,硕士,副研究员,主要研究方向为计算机网络技术、智能信息处理。E-mail: yangyumei7810@163.com。

(编辑：张诚)