自适应高斯厄米特粒子PHD滤波多目标跟踪算法

2016-07-04 10:31冯新喜

重庆邮电大学学报(自然科学版) 2016年2期

刘　欣，冯新喜，王　鹏

(空军工程大学信息与导航学院，陕西西安 710077)

刘欣，冯新喜，王鹏

(空军工程大学信息与导航学院，陕西西安 710077)

摘要：针对高斯厄米特粒子概率假设密度(probability hypothesis density, PHD)算法可能导致滤波计算复杂度较高、精度不强，性能较差的问题，提出一种自适应高斯厄米特粒子PHD的改进算法，该算法通过在高斯变换的过程中引入阈值，以该阈值为界剔除权值较小的积分点，对大于阈值的积分点进行归一化处理，在保证滤波精度的基础之上，减小权值较小点在计算上带来的冗余；另外在高斯厄米特滤波的过程中引入了自适应因子，适当调整高斯厄米特滤波过程中的增益，自适应调节滤波的均值与方差，以提高滤波过程的精度。仿真结果表明：改进后的算法相比于高斯厄米特粒子PHD算法在精度上有明显提高，同时简化了计算复杂度，达到预期的目的。

关键词：自适应滤波;高斯厄米特滤波;粒子PHD;多目标跟踪

0引言

传统的多目标跟踪通常采用关联算法[1-3]，将传感器得到的量测信息与航迹进行一一对应，这种关联方法引起的最主要的问题就是计算量过大，在进行多目标的跟踪过程中，要进行大量的计算，导致跟踪的实时性能较差。2001年Mahler提出了随机集[4]理论，这是多目标跟踪发展的一个里程碑。概率假设密度(probability hypothesis density，PHD)是随机集关于贝叶斯递推的后验概率密度的一阶矩，它有效地解决了数据关联带来的计算量过大的问题。

从实现方式上来看，PHD有2种实现方式[5]，一种是粒子PHD(sequential Monte Carlo-PHD, SMC-PHD)，另外一种是高斯混合PHD(Gaussian mixture-PHD, GM-PHD)。随后有许多学者对这2种实现方式分别进行改进，或将2者结合起来提出新的算法[6]以及对新算法进行改进。

文献[7]提出在原有的SMC-PHD的基础之上，使用高斯厄米特滤波产生高斯分布来拟合重要性密度函数，充分考虑了当前的量测信息，但是在整个滤波过程中，这种方法不能够充分利用有效信息解决异常状况对模型的干扰；高斯点的权值有大有小，较小的权值会使得滤波过程更加复杂，在计算量增大的同时，并不能有效地提高计算精度，这样仍然会出现滤波精度不高、性能较差的问题；针对这个问题，本文在高斯变换的过程中通过引入阈值[8]，剔除权值较小的高斯点，对相应权值较大的高斯点进行归一化处理；引入自适应因子[9]，自适应地调节高斯厄米特滤波得到的均值和方差，使得到的均值与方差充分利用了有效信息，得到的重要性密度函数与实际情况更加接近真实分布。

1高斯厄米特滤波[7-11]

经典的非线性扩展卡尔曼滤波方法[12]虽然解决了非线性滤波的问题，但是由于在滤波估计的过程中，过程噪声协方差和量测噪声协方差一直保持不变，这样容易产生误差累计，导致滤波发散[13]；传统的粒子滤波[14]通常选取系统状态变量的转移概率函数为重要性密度函数，这往往忽略了最新的观测信息，造成测量误差的增大[14]；高斯厄米特滤波是基于一种高斯厄米特数值积分的递归贝叶斯积分方法，它与无迹卡尔曼滤波[15]相同，都是确定性采样，并且不需要计算非线性函数的雅克比矩阵，它选取的采样点可以根据求积分点个数的不同而变换，因此，该算法的精度相对较高。

假设系统的状态方程与量测方程已知，系统噪声与量测噪声分别是ωk和vk，且它们是相互独立的具有零均值的高斯噪声，方差分别是Q和R；并且状态的后验概率密度可以用高斯分布近似表示。高斯厄米特滤波与传统的滤波算法相同，也是预测与更新的迭代过程，具体的步骤如下所示。

(1)

(2)

2)更新。根据预测得到的状态与方差，继续使用高斯变换公式，得到变换后新的高斯点，更新方程为

(3)

(4)

(3)—(4)式中，zk表示k时刻的观测值。其他各符号分别表示如下

(5)

(6)

(7)

(8)

2自适应高斯厄米特滤波的粒子PHD滤波算法

与高斯厄米特粒子PHD的滤波相同，自适应高斯厄米特粒子PHD进行滤波估计时也分为预测和更新2步，具体如下所示。

1)预测部分。假设k-1时刻目标的PHD是一个高斯混合形式，表示为

(9)

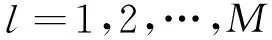
(10)

在选取积分点以及权值时，通常这些权值会有大有小，权值越大，对积分运算的贡献就越大，相反权值越小，对积分运算的贡献就越小。较小的权值不仅对积分运算的贡献较小，并且会引起计算量增大。基于此，文献[7]中通过引入权重阈值，丢弃权重较小的积分点，保留权重较大的积分点，可以相应降低计算量。

假设有m个积分点，阈值可以表示为

(11)

则当积分点的权值大于该阈值时，保留该积分点，反之则丢弃；然后将剩下的权值较大的积分点进行归一化处理。将该方法引入到高斯厄米特粒子PHD滤波的预测部分，可以降低计算的复杂度，提高计算效率。

接着，根据状态方程进行一步预测

(12)

预测后的状态均值和方差分别是

(13)

(14)

继续选取M个精确的高斯点，对得到的预测状态和方差继续进行高斯变换，高斯变换的方法与上面的方法相同，也要经过阈值的剔除和重新归一化

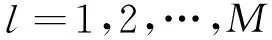
(15)

量测预测为

(16)

粒子更新方程为

(17)

(18)

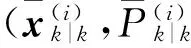
(19)

(20)

用自适应因子对增益函数进行修正，得到的新增益为

(21)

因此，(19)—(20)式中的滤波更新方程可以表示为

(22)

(23)

新增益合理地利用有效信息，对均值和方差进行修正，这样能够抑制异常情况对模型的干扰，从而使得更新部分的重要性密度函数更加接近真实情况。

(22)—(23)式中，z(j)是k时刻通过传感器得到的量测值，其余的参数计算方法与(6)—(8)式的一致。得到的更新后的状态与方差分别为

(24)

(25)

通常情况下，预测PHD包含存活部分与新生部分，为了简化问题，通常将衍生部分忽略不计，那么预测PHD为

(26)

如上所述，预测的PHD可以表示为一个高斯混合的形式。

2)更新部分。得到预测的粒子的状态与方差后，并把它们作为更新部分的重要密度函数，即：

(27)

在重要密度函数中进行抽样，得到N个采样粒子：

(28)

每个粒子的权值计算公式为

(29)

(30)

更新后的PHD表示为

(31)

(31)式中，各个参数的计算方式为

(32)

(33)

(34)

用自适应因子对增益进行调节，可以更合理地利用有效信息，这样可以控制状态异常对估计状态和方差的影响，使得到的重要性密度函数更加接近真实分布。

3实验仿真

通过对系统的状态进行分析，将本文的算法与高斯厄米特粒子PHD算法进行比较分析。

仿真实验在二维平面中进行，假设目标数目是未知的且随着时间的变化而不断变化的，目标的运动模型和量测模型分别是

(35)

(36)

Si表示第i个传感器的位置信息。实验中采用2个相同的观测站对目标进行独立地跟踪，位置信息分别为S1(0 m,0 m)，S2(0 m,500 m)。目标的存活概率和检测概率均是0.95，

仿真场景中共有3个目标做匀速运动，目标的运动参数如表1所示，忽略目标的衍生情况，新生目标的PHD表示为

(37)

表1　目标初始运动参数

图1—图3是实验的仿真结果。图1是目标的运动轨迹对比图，从图1中我们可以清楚地看出改进的自适应算法相比于高斯厄米特粒子PHD算法，更加接近目标的实际运动轨迹。

图2表示的是目标的运动数目的比对图。在20 s时，目标3出现。高斯厄米特算法在第3个目标出现时会出现很多误判点，相比于自适应算法来说，计算精度低。采用改进的自适应算法计算运动场景中的目标数目，得到的结果与实际的情况大体一致，计算精度较高。

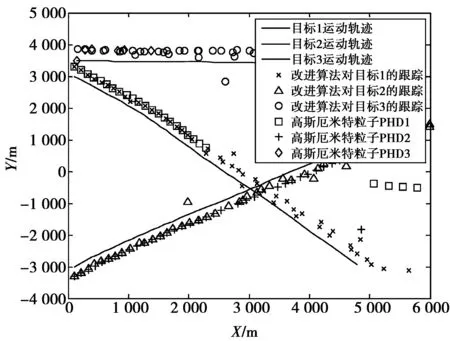
图1　目标跟踪轨迹对比图Fig.1　Target tracking trajectory comparison

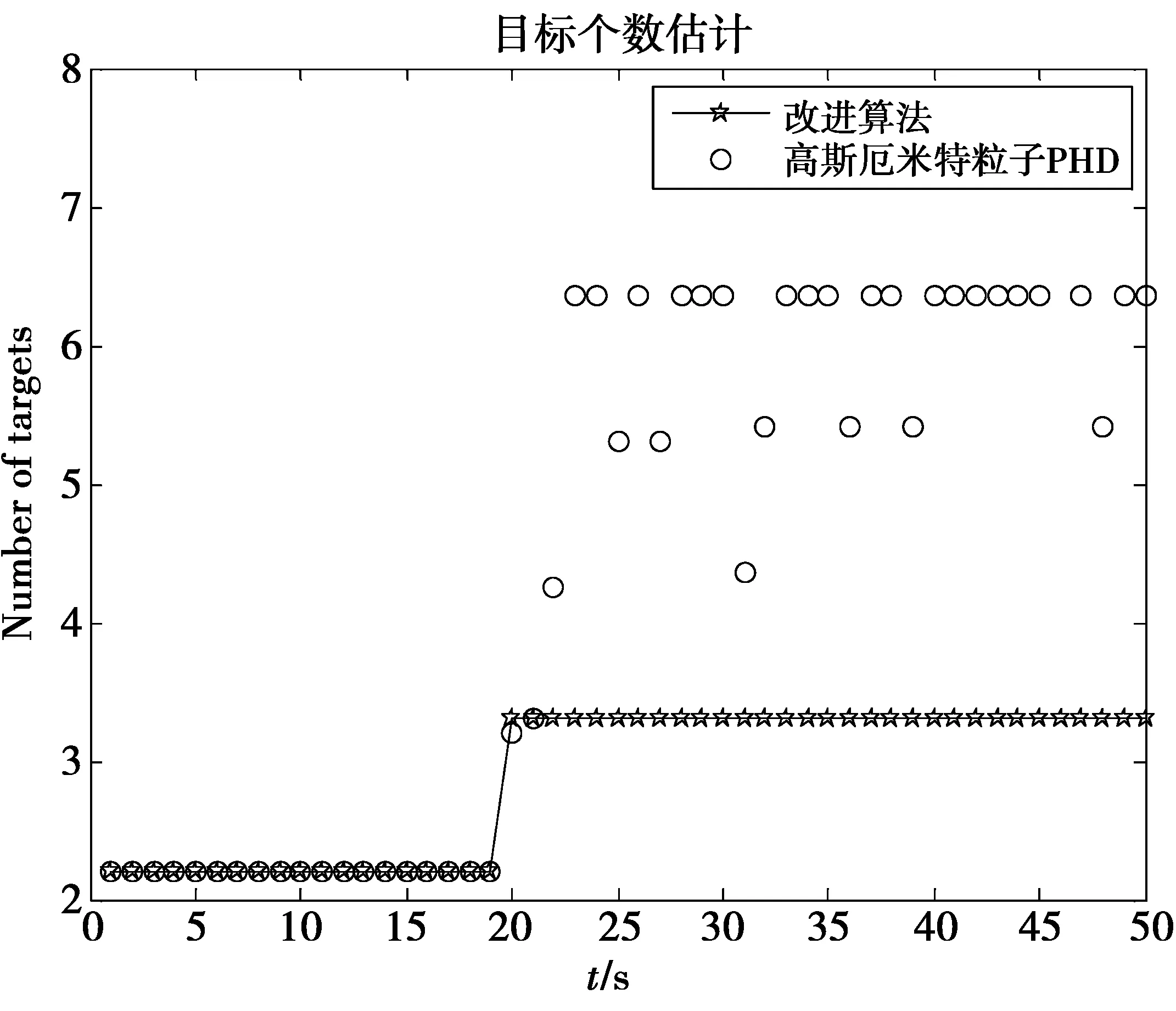
图2　目标数目图Fig.2　Target number

图3中表示的是高斯厄米特粒子PHD算法与改进的自适应算法的误差对比图。由图中可以很明显地看出改进的算法在精度对比上相比于高斯厄米特算法来说有很明显的提高。

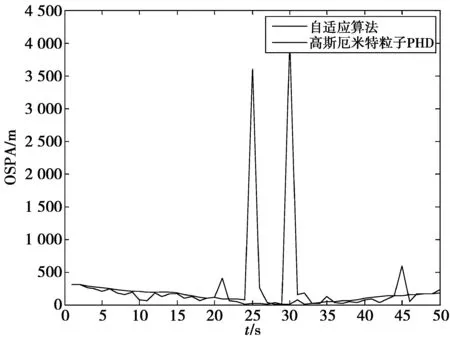
图3　滤波误差图Fig.3　Filter error comparison

4结论

本文在高斯厄米特粒子PHD的基础之上，进行了自适应修正，设定阈值，筛选出权值较大的积分点，并对其权值进行归一化；引入自适应因子，对增益矩阵进行修正，得到的均值与方差更能反映实际的跟踪过程中预测得到的均值与方差，得到的重要性密度函数也与真实情况更加接近。仿真结果表明了改进的自适应算法相比于高斯厄米特粒子PHD算法，在精度上有了进一步的提高。

参考文献：

[1]R.A.Singer, R.G.Sea. New results in optimizing Surveillance System Tracking and Data Correlation performance in Dense Multi-target Environments[J]. IEEE Transactions. Automatic Control, 1973,18(6):571-582.

[2]何友，唐劲松.进程武器系统多目标航迹处理算法研究[C]//烟台：海军航空工程学院，1991.

HE You, TANG Jinsong. Multi-target course processing algorithm research on Process Weapon System[C]// Yantai: Navy Aeronautical Engineering Institute,1991.

[3]韩崇昭，朱洪艳.多源信息融合[M].2版.北京：清华大学出版社，2010.

HAN Chongzhao, ZHU Hongyan. Multiple source Information Fusion[M].2nd ed. Beijing: Qinghua University Press,2010.

[4]MAHLER R. A theoretical foundation for the Stein-Winter probability hypothesis density (PHD) multi-target tracking approach[C] Proceedings of the MSS National Symposium on Sensor and Data Fusion, SanAntonio TX:[s.n], 2000: 99-117.

[5]周承兴，刘贵喜，侯连勇，等.改进的高斯粒子概率假设密度滤波算法[J].控制理论与应用,2011,28(7): 1005-1008.

ZHOU Chengxing, LIU Guixi, HOU Lianyong, et al. Improved Gaussian Partical Probabitity Hypothsis Density Filter[J]. Control Theory and Application,2011,28(7):1005-1008.

[6]CLARK D, VO B T, VO B N. Gaussian particle implementations of probability hypothesis density filers[C]//2007 IEEE Aerospace Conference. Big Sky MT:[s.n], 2007: 1-11.

[7]杨金龙，姬红兵，刘进忙.高斯厄米特粒子PHD被动测角多目标跟踪算法[J].系统工程与电子技术，2013，30(3),457-462.

YANG Jinlong, JI Hongbing, LIU Jinmang. Gaussian Hermit Partical PHD Passive angle measurement in multi-target tracking[J]. System engineering and electronic technology,2013,30(3),457-462.

[8]李昱辰，李战明.基于修正积分卡尔曼粒子滤波的自适应目标跟踪算法[J].计算机应用研究，2012,29(7)：2776-2779.

LI Yuchen, LI Zhanming. Adaptive target tracking algorithm based on modified integral kalman filter[J]. Computer application research. 2012,29(7):2776-2779.

[9]薛丽，高社生，胡高哥.自适应GHPF及其在组合导航中的应用[J].计算机仿真，2013,30(5):108-111.

XUE Li, GAO Shesheng,HU Gaoge. Adaptive GHPF and application in integrated Navigation[J]. Computer simulation. 2013,302(56):108-111.

[10] IENKARAN A, SIMON H, ROBERT J E. Discrete-time nonlinear filtering algorithm using Gauss-Hermit quadrature [J]. Proceedings of the IEEE,2007,95:953-977.

[11] 袁泽剑，郑南宁，贾新春.高斯厄米特粒子滤波器[J].电子学报，2003,31(7):970-973.

YUAN Jianze, ZHENG Nanjing, JIA Xinchun. Gaussian Hermit Partical Filter[J]. Electronic Journal,2003,31(7):970-973.

[12] 程咏梅，潘泉，张洪才,等. 基于推广卡尔曼滤波的多站被动式融合跟踪[J].系统仿真学报，2003,15(4)：548-550.

CHENG Yongmei, PAN Quan, ZHANG Hongcai,et al. Multiple Station Passive Fusion Tracking based on extended Kalman Filter[J]. Jounal of system simulation, 2003,15(4):548-550.

[13] 何友，修建娟.雷达数据处理及应用[M].北京:电子工业出版社，2005.

HE You, XIU Jianjuan. Radar Data Fusion and Application [M]: Beijing, Electronic Industry Press, 2005.

[14] 张诗柜，朱立新，赵义正. 粒子滤波算法研究进展与展望[J].自动化技术与应用，2010,29(6):1-9.

ZHANG Shigui, ZHU Lixin, ZHAO Yizheng. Research Progress and Prospect on Partical Filter Algorithm[J]. Automation technology and application,2010,29(6):1-9.

[15] JULIER S J. UHLMANN J K. A new Extension of the Kalman Filter to Nonlinear System[J]. SPIE, Vol.3068,1997:182-193.

Adaptive Gauss Hermite particle PHD filter in multi-target tracking algorithm

LIU Xin, FENG Xinxi, WANG Peng

(Institute of Information and Navigation, Air Force Engineering University, Xi’an 710077, P.R.China)

Abstract:Aiming at complex calculation, low accuracy and poor performance of Gaussian Hermite Particle PHD algorithm, an adaptive algorithm is proposed. The new algorithm adopts two ways to improve the performance, on one hand, a threshold is proposed to eliminate integral points with less weight, and then normalizes the remaining points in the Gaussian transformation. Adopting this way, the measure not only ensures the accuracy of the algorithm, but also reduces the computation complexity. On the other hand, the new algorithm also introduces an adaptive factor to adjust gain, mean value and variance also correspondingly change in the filtering process. The improved method can improve the accuracy of the algorithm. The simulation results show that the proposed algorithm has an improved accuracy and achieves the desired effect.

Keywords：adaptive filtering; Gaussian Hermite filtering; particle PHD; multi-target tracking

DOI：10.3979/j.issn.1673-825X.2016.02.022

收稿日期：2015-03-11

修订日期：2015-12-23通讯作者：刘欣lxxh26@163.com

基金项目：国家自然科学基金(61403414)

Foundation Item：The Natural Science Foundation of China(61403414)

中图分类号：TP242

文献标志码：A

文章编号：1673-825X(2016)02-0280-05

作者简介：