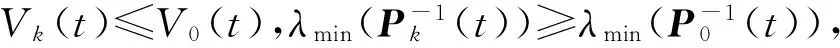基于时变神经网络的迭代学习辨识算法

戴　蓉，黄　成

(1.中国民用航空飞行学院 计算机学院,四川 广汉 618307; 2.四川工程职业技术学院,四川 德阳 618000)



基于时变神经网络的迭代学习辨识算法

戴蓉1，黄成2

(1.中国民用航空飞行学院 计算机学院,四川 广汉 618307; 2.四川工程职业技术学院,四川 德阳 618000)

摘要：为了实现在有限时间区间上可重复运行的离散时变非线性系统辨识，给出基于时变神经网络的迭代学习辨识算法。对于每一个固定时刻，以该时刻的神经网络逼近该时刻系统输入输出间的映射关系,提出了在同一时刻沿迭代轴训练网络权值的带死区迭代学习最小二乘算法，为防止收敛速度下降过快，进一步提出了协方差阵可重调的改进算法。所提算法有较快的收敛速度，且时变神经网络对非线性时变系统的辨识精度也较高。

关键词：系统辨识；非线性时变系统；时变神经网络；迭代学习；最小二乘

0引言

由于线性系统的特性关于参数是线性的，人们可以推广已有线性系统辨识方法，给出可线性参数化的非线性动态系统的参数估计。这些参数估计算法往往只适合辨识定常或慢时变参数系统。已提出的针对时变参数系统的辨识方法如带遗忘因子的最小二乘法[1]、卡尔曼滤波法[2]等，通常是沿时间轴对时变参数进行跟踪，估计误差能沿时间轴实现有界收敛。

迭代学习辨识方法适于解决在有限时间区间上可重复运行的动态系统的时变参数估计问题。在一定条件下，该方法可对系统实现完全辨识任务，使整个有限时间区间上的估计误差沿迭代轴收敛到零。文献[3]针对一类含有未知时变参数的离散时变系统，给出了迭代学习投影和迭代学习最小二乘2种算法。通过在同一时刻沿迭代轴估计系统的未知时变参数，此类辨识方法可使整个有限时间区间上的估计误差沿迭代轴逐点收敛到零。对于系统存在未建模动态或存在外界扰动时的情形，需要进一步研究。

已证明神经网络对非线性连续函数具有良好的逼近能力[4-6]。近年来，以神经网络辨识非线性定常系统方面的研究成果很多[7-10]。 已有文献中神经网络的权值大多是沿时间轴进行训练，训练完后网络的输入与输出之间的映射关系是固定不变的，而时变系统的输入输出之间的映射关系会随时间不断变化，这要求神经网络的输入输出之间的映射关系也能随时间变化。 文献[11]将权值当作系统的未知时变参数，利用卡尔曼滤波算法对其进行估计，取得了较好的辨识效果。但该算法仍旧是沿时间轴估计权值，估计误差能沿时间轴实现渐近收敛。本文所要研究的问题是如何在一有限时间区间上利用神经网络完全辨识非线性时变系统。

本文针对在有限时间区间上重复运行的非线性离散时变系统， 提出基于时变神经网络辨识的迭代学习辨识算法。其主要方法是：对于每一个固定时刻，以该时刻的神经网络逼近该时刻系统输入输出间的映射关系。本文提出在同一时刻沿迭代轴训练网络权值的带死区迭代学习最小二乘算法。考虑算法收敛性能，本文进一步提出一种协方差阵可重调的改进算法。理论分析表明，所提算法可以保证整个有限时间区间上的估计误差沿迭代轴逐点收敛到原点的邻域内，邻域半径取决于神经网络的建模精度。仿真结果进一步验证了所提算法的有效性。

1时变神经网络

神经网络能以任意精度逼近紧集上的任意非线性连续函数，常用于非线性复杂系统的建模与控制。

本文考虑一类时变神经网络。与传统的含定常权值的神经网络不同，该类网络的输入、输出与权值均可随时间变化。一类多输入单输出的时变神经网络可表示为

(1)

(1)式中：x(t)=[x1(t),x2(t),…,xn(t)]T∈Rn为网络输入向量；y(t)为网络输出标量；W(t)=[w1(t),…,wl(t)]T为可调的时变权值向量；φ(x(t))=[φ1(x(t)),φ2(x(t)),…,φl(x(t))]T为激励函数向量组，l为神经元节点数。

激励函数φ(·)的选择很多，如阶跃函数，Logistic函数，高斯函数等。以高阶神经网络为例，激励函数可选为

(2)

(3)

假设对于有界的xj(t)可得有界的φ(xj(t))，事实上很多激励函数均满足此条件。因此，对于有界的x(t)，有

(4)

非线性时变系统广泛存在于实际系统中，本文以上述时变神经网络逼近未知时变映射f(x(t),t)，从而达到辨识目的。事实上，对于每一个特定的时刻t=t*∈[0,T],f(x(t),t)是关于x的非线性函数。因此，对于每一确定的时刻t，时变神经网络就退化为传统的神经网络。

2非线性离散时变系统辨识

考虑下述可重复运行的SISO非线性离散时变系统

(5)

(5)式中：n>0,m>0;f(·)为未知的光滑非线性时变函数；t∈{0,1,…,T}为一有限的时间区间；k∈{0,1,… }为迭代次数。

记

则系统(5)可重写为

(6)

设系统(6)的时变神经网络模型为

(7)

(8)

(9)

定义估计误差ek(t+1)为

(10)

我们的辨识目标是寻找时变权值W(t)的估计值Wk(t)，t∈{n-1,n,…,T-1}，使得当迭代次数k足够大时，整个辨识区间t∈{n,…,T}上的估计误差ek(t)能尽可能小。

系统初值{yk(0),yk(1),…,yk(n-1)}是由初始条件确定，这里仅考虑有限辨识区间t∈{n,…,T}上的估计误差。

2.1带死区迭代学习最小二乘算法

为克服神经网络建模误差项的影响，依据文献[12]中的带死区最小二乘算法，在设计权值更新律时，给出一种带死区的迭代学习最小二乘算法。本算法中的神经网络权值是在同一时刻沿迭代轴进行训练。该迭代算法为

(11)

(12)

(11)—(12)式中：初值W0(t)，t∈{n-1,n,…,T-1}给定有界；协方差阵P0(t)，t∈{n-1,n,…,T-1}取成对阵正定阵；ak(t)为

ak(t)=

(13)

迭代学习算法(11)—(13)中，权值是沿迭代轴k而非时间轴t进行估计。根据(11)式，当计算Wk+1(t)时，需要计算ek(t+1)，沿时间轴t看ek(t+1)是非因果的，而沿迭代轴k看它是可计算的。

2.2收敛性分析

对迭代学习算法(11)—(13)进行收敛性分析。

定理1对于系统(6)，学习算法(11)—(13)具有以下性质。

证明根据(8)—(10)式可得

(14)

在(11)式两边减去W(t)可得

(15)

将(14)式代入(15)式可得

(16)

(17)

将(17)式代入(16)式整理得

另外，根据矩阵求逆引理[12]易得

(18)

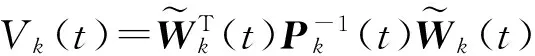
Vk+1(t)-Vk(t)=

(19)

将(15)式、(18)式代入(19)式并整理得

Vk+1(t)-Vk(t)=

(20)

将

代入(20)式可得

(21)

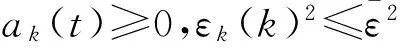
(22)

下面根据(13)式分2种情况讨论:

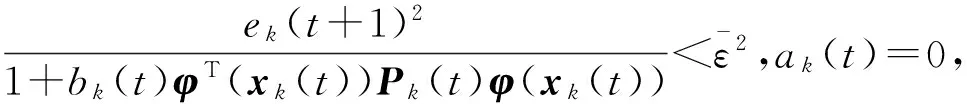
根据式(21)可得

(23)

由(18)式可知，Pk(t)为一对称正定矩阵，又bk(t)>0，所以有

因此

(24)

又0

在上式两边对k进行累加得

因为V0(t)有界，bk(t)>0，所以

(25)

根据(12)式可得

(26)

(27)

记ck(t)=bk(t)φT(xk(t))Pk(t)φ(xk(t))，根据bk(t)的定义有

(28)

根据(25)式可得

(29)

又xk(t)∈S有界，根据(4)式可知(29)式的分母项有界，结合(28)式有

(30)

综合以上2种情况可得

(31)

(32)

因此Vk(t)是非负的不增序列。

由(18)式可得

(33)

结合(32)式可得

(34)

即有

(35)

(36)

又根据(31)式直接可得

(37)

这就保证了估计误差的一致有界收敛性，性质(ii)得证。

3协方差阵可重调的改进算法

我们发现，随着迭代次数的增加，(12)式中的协方差阵Pk(t)会变得很小，算法的收敛速度会急剧下降。为使算法始终保持较快的收敛速度，将(12)式中Pk(t)的更新律做如下改进[12]，即当Pk(t)的迹小于某个设定的值时应对其重调。设{Ks}={k1,k2,…}为重调Pk(t)的迭代序列。

当k∉{Ks}时，就按(12)式的更新律来校正Pk(t)，即

(38)

当k=ki∈{Ks}时，Pki+1(t)应重调如下

(39)

定理2对于系统(6)，以上改进算法(11)，(13)，(38)，(39)具有以下性质

证明对于k=0,1,…,k1，定义

(40)

Vk+1(t)-Vk(t)=ak(t)

Vk+1(t)

(41)

(42)

k=0,1,…,k1

(43)

又根据(32)式可得

(44)

又因为

(45)

将(44)式，(45)式代入(43)式可得

(46)

同理，当k1

(47)

(48)

依次类推，对所有的k，有以下不等式成立

(49)

(50)

性质(II)得证。

因此，与第3部分中的带死区迭代学习最小二乘算法一样，该协方差重调算法仍能保证时变权值估值的有界性和估计误差的一致有界收敛性。

4数值仿真

例1考虑如下可重复运行的非线性离散时变系统[10]

其中，t=0,1,…,100，初值yk(0)=0.1rand。

测试阶段：当k=26时，在一个非训练的测试序列[10]

uk(t)=0.15sin(2tπ/250)+

0.22sin(2tπ/35)+0.2

激励下，得到的均方根误差为4.08×10-5，图3给出了网络辨识结果。

图1　估计误差的收敛过程Fig.1　Convergence process of estimation error

图(t)的收敛过程Fig.2　Convergence process of(t)

图3　k=26时测试序列输入下的辨识效果Fig.3　Identification results of test sequence input withk=26

例2考虑如下可重复运行的时变NARMAX模型[11]

其中，t=0,1,…,100，初值yk(0)=0.1rand。

图4　估计误差的收敛过程Fig.4　Convergence process of estimation error

图5　k=25时神经网络获得的权值Fig.5　Neural networks to get the weight with k=25

测试阶段：当k=139时，在与例1相同的非训练测试序列uk(t)激励下，得到均方根误差为1.74×10-4，图6给出了网络辨识结果。

图6　k=139时测试序列输入下的辨识效果Fig.6　Identification results of test sequenceinput with k=139

通过以上2个算例对本文所提方法进行了验证。数值结果表明，本文所提的学习算法具有较快的收敛速度，且时变神经网络对非线性时变系统的辨识精度也较高。

5结论

本文通过构造时变神经网络模型，给出在同一时刻沿迭代轴训练网络权值的带死区迭代学习最小二乘算法及协方差阵可重调的改进算法，讨论了一类非线性离散时变系统有限时间区间上的完全辨识问题。理论分析与仿真结果均表明，所述算法能保证整个有限时间区间上的估计误差顺着迭代轴逐步收敛到原点的邻域空间中，建模精度则直接影响着该邻域半径的大小。本文所提的学习算法具有较快的收敛速度，且时变神经网络对非线性时变系统的辨识精度也较高。

参考文献：

[1]DING F, CHEN T. Performance bounds of forgetting factor least-squares algorithms for time-varying systems with finite measurement data [J]. Circuits and Systems, 2012, 52(3): 555-566.

[2]李书进, 李文华. 基于自适应卡尔曼滤波的时变结构参数估计[J].自动化学报, 2011, 29(2): 146-149.

LI Shujin, LI Wenhua. Adaptive Calman filter based on the parameter estimation of time-varying structures[J]. Acta Automatica Sinica, 2011, 29 (2): 146-149.

[3]SUN M,HE X.Iterative learning identification and control of discrete time-varying systems[J].Proceedings of the 26th Chinese Control Conference,2013,3(7):520-524.

[4]徐凤霞, 朱全民, 赵东亚, 等. 基于 U 模型的非线性控制系统设计方法十年发展综述[J]. 控制与决策, 2013, 28(7): 961-971.

XU Fengxia, ZHU Quanmin, ZHAO Dongya, et al. Nonlinear U model of the control system design method based on ten years of the development review[J]. Control and Decision, 2013, 28 (7): 961-971.

[5]吴龙庭, 曹顺安, 胡家元, 等. 时滞系统的 LM-Smith 神经网络控制器[J]. 计算机应用研究, 2014, 31(4): 1042-1044.WU Longting,CAO Shunan,HU Jiayuan,et al.A LM-Smith neural network controller for time delay system[J].Application Research of Computer,2014,31 (4):1042-1044.

[6]严伟力, 孙明轩. 基于时变神经网络的非线性时变系统建模[J]. 小型微型计算机系统, 2011, 32(6): 1228-1231.

YAN Weili, SUN Mingxuan. Nonlinear time-varying neural networks with time-varying system modeling [J]. Mini micro Systems, 2011, 32 (6): 1228-1231.

[7]ZHAO H, ZHANG J. Nonlinear dynamic system identification using pipelined functional link artificial recurrent neural network[J]. Neurocomputing, 2012, 72(13): 3046-3054.

[8]SCHÖN T B, WILLS A, NINNESS B. System identification of nonlinear state-space models [J].Automatica, 2013, 47(1): 39-49.

[9]曹伟,丛望,李金,等.基于迭代学习的离散线性时变系统故障诊断[J].控制与决策,2013,28(1):137-140.

CAO Wei, CONG Wang, LI Jin, et al. The discrete linear iterative learning system based on the fault diagnosis of [J]. Control and Decision, 2013, 28 (1): 137-140.

[10] ZHANG D, ADELMAN D. An approximate dynamic programming approach to network revenue management with customer choice [J]. Transportation Science, 2014, 43(3): 381-394.

[11] 徐小平, 钱富才, 王峰. 非线性系统辨识方法研究[J]. 计算机工程与应用, 2012, 46(6): 19-24.

XU Xiaoping, QIAN Fucai, WANG Feng. Nonlinear system identification method on [J]. Computer Engineering and Applications, 2012, 46 (6): 19-24.

[12] GAO J, SULTAN H, HU J. Denoising nonlinear time series by adaptive filtering and wavelet shrinkage: a comparison[J]. Signal Processing Letters, 2013, 17(3): 237-240.

Iterative learning identification algorithm based on time-varying neural network

DAI Rong1，HUANG Cheng2

(1.Department of Computer Science, Civil Aviation Flight University of China, Guanghan 618307,P.R.China;2. Sichuan Engineering Technical College, Deyang 618000, P.R.China)

Abstract:In order to achieve that the discrete time-varying nonlinear system identification can run repeateadly on the finite time interval, an iterative learning identification algorithm based on time-varying neural networks is given.First, for each fixed time, the neural network of the moment which approachs the mapping relationship between input and output of the system,the iterative learning least squares algorithm with dead-zone for the weights updating along the iteration axis is proposed. To prevent the convergence rate from falling too fast, the improved algorithm whose covariance matrix can be retuned is proposed further. The proposed algorithm guarantees that the estimation error converges to a bound point wisely over the entire time interval, and the neighborhood radius depends on the modeling accuracy of the neural network. Experimental results show that the proposed algorithm has a faster convergence rate, and identification accuracy of the time-varying neural networks for nonlinear time-varying system is higher.

Keywords：system identification; discrete-time varying nonlinear systems; time-varying neural networks; iterative learning; least squares

DOI：10.3979/j.issn.1673-825X.2016.02.020

收稿日期：2014-12-19

修订日期：2015-11-26通讯作者：黄成dair1977@163.com

基金项目：四川省教育厅科研项目(13ZA0135)

Foundation Item：The Sichuan Provincial Department of Education research (13ZA0135)

中图分类号：TP273

文献标志码：A

文章编号：1673-825X(2016)02-0265-08

作者简介：

戴蓉(1977-)，女，四川攀枝花人，副教授，硕士，主要研究方向为计算机仿真、数据库技术、多媒体技术。

黄成，(1975-)，男，江苏常州人，副教授，学士，主要研究方向为网络工程、信息安全，网络编程。E-mail: dair1977@163.com。

(编辑：张诚)