基于粒子群算法的双子支持向量机研究

摘要:针对标准支持向量机训练时间过长与参数选择无指导性问题,给出一种通过粒子群优化双支持向量机模型参数的方法。与标准支持向量机不同,该方法的时间复杂度更小,特别适合不均衡的数据样本分类问题,对求解大规模的数据分类问题有很大优势。将该算法与标准的支持向量机分类器在不同的文本数据集上进行仿真实验对比,以验证算法的有效性。结果表明基于粒子群优化的双子支持向量机分类器的分类结果高于标准支持向量机分类结果。
关键词:双子支持向量机(TWSVM);分类算法;粒子群优化算法(PSO)
DOIDOI:10.11907/rjdk.151455
中图分类号:TP312
文献标识码:A 文章编号:16727800(2015)006007204
基金项目:玉林师范学院校级科研项目(2014YJYB04)
作者简介作者简介:刘建明(1986-),男,广西博白人,硕士,玉林师范学院数学与信息科学学院助教,研究方向为数据挖掘与机器学习。
0 引言
粒子群优化算法[1](Particle Swarm Optimization,PSO)是由美国研究学者Kennedy等人在1995年提出的,PSO算法每一代的种群中的解具有向“他人”学习和“自我”学习的优点,该算法能在较少的迭代次数中找到全局最优解,这一特性被广泛应用于神经网络方法、函数优化问题、数据挖掘、模式识别,工程计算等研究领域。
双子支持向量机(Twin Support Vector Machines, TWSVM)是Jayadeva[23] 基于传统支持向量机在2007年提出来的。TWSVM是从SVM演化而来的,是一种新型的基于统计学习理论的机器学习算法。TWSVM具有SVM优点,同时适合处理像文本自动分类、基因表达、空间信息遥感数据、语音识别等这样的大规模数据分类问题。
针对TWSVM对惩罚参数和核函数参数缺乏指导性问题,本文结合PSO算法的优点,给出一种基于PSO的
算法优化改进策略,对TWSVM分类器进行优化。PSO是一种基于群体智能的全局寻优算法,该算法能在较少的迭代次数中找到全局最优解,通过利用粒子群优化算法对双子支持向量机进行优化后,分类器较之标准支持向量机有更好的分类效果。
1 PSO算法
PSO算法步骤:①初始化粒子群,利用随机函数法给每一个粒子的初始位置和速度赋值;②根据第①步的赋值及初始位置与速度更新每一个粒子新的位置;③利用选定的适应度函数计算每一个粒子的适应度值;④对每一个粒子,对比其个体和群体的适应度值,并找出粒子经过的最好位置的适应度值,如果发现更好的位置及适应度值,那么就更新其位置;⑤根据公式更新每个粒子的速度与位置,如果找到最优的位置或者是到了最大的迭代次数,算法终止,否则转入第3步继续迭代求解。
2 双子支持向量机(TWSVM)
与SVM不同,TWSVM求解的是一对分类超平面,SVM求解一个QP问题而TWSVM解决的是两个QP问题,而这两个QP问题的求解规模比SVM小很多。传统SVM构造两个平行的超平面,并且使两个超平面之间的距离最大即最大间隔化,TWSVM虽然也是构造超平面,但超平面之间不需要平行。TWSVM对每一个样本都构造一个超平面,每个样本的超平面要最大限度地靠近该类的样本数据点,而同时尽可能地远离另一类样本数据点。新数据样本将会分配给离两个超平面中最近的一个平面。事实上,该算法还可以沿着非平行面聚集,而且样本聚集方式是根据完全不同的公式聚合而成的。实际上,在TWSVM中的两个QP问题与标准SVM的QP问题除了求解约束问题不同外,求解公式是相同的。TWSVM的二分类算法通过求解下面的一对QPP(Quadratic Program Problem)问题进行二次规划优化[5]。
其中,c1,c2>0并且e1和e2是适当维数且属性值是全为1的向量。TWSVM算法为每一个类构建超平面时,样本点根据与各个超平面的距离大小作为与平面靠近程度的评价指标,目标函数(2)和(3)计算样本点与超平面距离的平方。因此,它的最小值能保证样本数据点最大限度地靠近其中一类(类一),同时尽可能地远离另一类。误差变量用于测量超平面距离间隔的误差。目标函数公式(2)和(3)的第二项是误差之和,它的作用是使错分样本的数据极小化,尽量减少错分的误差情况。为求解公式(2)和(3),分别对TWSVM1和TWSVM2引入拉格朗日函数,通过KKT条件分别求得其对偶问题如公式(4)和(5)[6]所示。
3 基于PSO的TWSVM分类算法
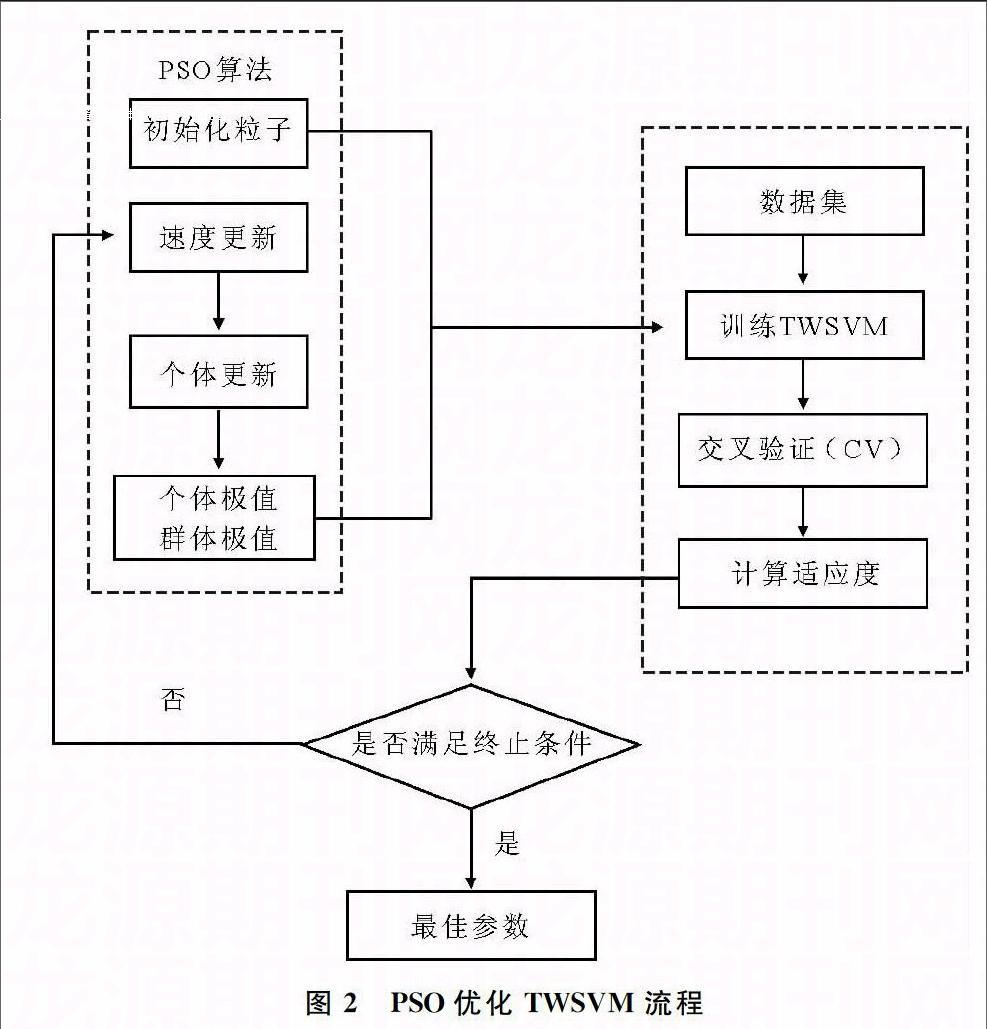
在TWSVM中,与SVM相同,都需要对参数进行确定,TWSVM对每个类均有一个惩罚参数和核函数参数。不同的惩罚参数和核函数参数影响分类的准确率,而PSO算法拥有全局的优化能力,因此,本文将PSO算法引入TWSVM中,解决TWSVM参数的选择问题,PSOTWSVM算法不仅能提高TWSVM的准确率同时又能降低SVM的训练时间,提高训练效率。图2展示了应用PSO算法对TWSVM参数选择的优化流程。
基于PSOTWSVM分类算法:①根据样本训练数据集每个类别,随机选定惩罚参数Cm,m=1,2,…,k以及核函数;②应用PSO算法对训练进行参数优化,找出最佳惩罚参数和核函数参数的最优值;③利用公式(3)、(4)求解样本数据对偶问题,构造样本空间的逼近超平面F(x)i=1,2,…k=K(x,c)wi+bi;④对每一类样本数据求得逼近超平面后,再求解判别函数(10);⑤将测试样本数据集利用判别函数进行分类预测。
传统SVM是基于二分类提出的,其复杂度为O(n3),其中n为样本数目[2]。然而在TWSVM二分类算法中,设每类样本数据为n/2,因此,求解两个优化问题时间复杂度为:O(2*(n/2)3),所以在二分类问题中的TWSVM时间复杂度为传统SVM的1/4。推广到多分类问题时,可以发现在时间复杂度方面,TWSVM求解优化问题的时间更少。例如样本类别数为k类,那么该样本的时间复杂度为O(k*(n/k)3)。由于TWSVM分类算法对每类都构造一个超平面,因此该算法在处理不平衡数据时,即一类的样本数目比另一类的样本大得多情况时,TWSVM分别实施不同的惩罚因子,TWSVM克服了传统的SVM处理不均衡样本的局限性,这一点非常适用于大规模的不均衡分类问题。
4 算法仿真实验
为验证基于PSO的TWSVM分类算法的有效性,本文利用该算法构建一个文本分类器,运用不同数据集在该分类器上进行实验并与标准支持向量机构建的分类器进行对比仿真实验。
4.1 分类器性能评价
常用的分类器评价方法包括:准确率和召回率。这两个指标广泛应用于文本分类系统的评价标准。准确率(Precision)是指全部分类文本中划分的类别与实际类别相同的文本数量占全部文本的比率。召回率(Recall)是指分类正确的文本数占应有文档数的比率。文本分类输出结果见表1。
4.2 实验结果分析
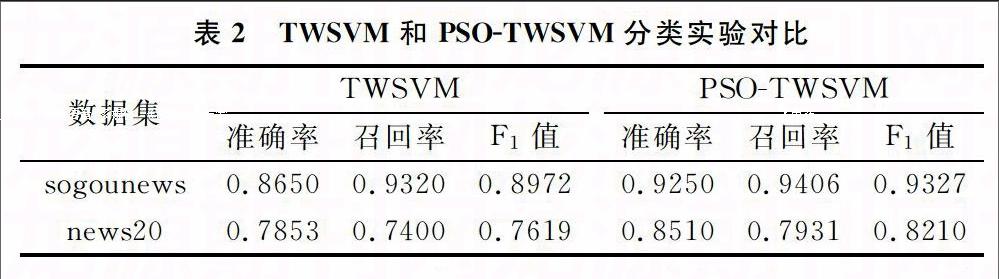
本实验所采用的文本数据为搜狗分类新闻语料库(Sogounews)(选取其中一类进行)和20组新闻数据(经典的文本分类数据集)。搜狗新闻数据预处理的特征词选择方法为IG(信息增益),该实验数据包含150个文本特征属性,样本数据为1600,其中1000为训练集,600为测试集,数据集分别为新闻、非新闻两类。News20选择台湾大学林智仁教授整理后的News20数据集作为实验数据,整理后的News20样本数规模和特征项较高,所以只选取了其中的800个文本样本并对特征项进行降维处理后进行实验,验证TWSVM分类算法和基于PSO的TWSVM分类算法性能。实验采用的核函数是线性核函数,初始惩罚参数和核参数分别为2和0.1,粒子群种群数量为30,迭代次数200,c1和c2取值均为1.5,实验结果如表2所示。
由表2可知,PSOTWSVM的分类性能比TWSVM要好。因此,基于PSO的TWSVM是一个有效算法。该算法不但比标准的SVM算法训练时间更短,而且比TWSVM有更好的准确率,PSOTWSVM解决了TWSVM的参数选择问题,提高了TWSVM的泛化性。
5 结语
通过基于PSO的TWSVM分类算法与TWSVM算法的分类对比实验可知,应用PSO算法的全局寻优能力提高了TWSVM分类的能力。PSO优化后TWSVM分类器的性能更为优越。基于PSO的TWSVM分类算法比标准的SVM时间复杂度更小,比TWSVM的准确率更高,基于PSO的TWSVM算法在分类问题上较之传统的SVM算法有更大的优越性。
参考文献:
[1]许国根,贾瑛.模式识别与智能计算的MATLAB实现[M]. 北京:北京航空航天大学出版社,2012.
[2]JAYADEVA,R KHEMCHANDAN, S CHANDRA.Twin support vector machines for pattern Classification[J]. IEEE Trans. Pattern and Machine Intelligence,2007,29(5):905910.
[3]SHIFEI DING, JUNZHAO YU, BINGJUAN QI,et al. An overview on twin support vector machines[J]. Springer Science Business Media. August 2014,2(42): 245252.
[4]谷文成,柴宝仁,腾艳平. 基于粒子群优化算法的支持向量机研究[J].北京理工大学学报,2014, 34(7):705 709.
[5]M A KUMAR,M GOPAL.Application of smoothing technique on twin support vector machines[J]. Pattern Recognition Letters, 2008,29(13):18421848.
[6]王振.基于非平行超平面支持向量机的分类问题研究[D].长春:吉林大学,2014.
[7]M ARUN KUMAR,M GOPAL. Least squares twin support vector machines for pattern classification[J]. Expert Systems with Applications, 2009,4( 36): 75357543.
[8]YUAN HAI SHAO,ZHEN WANG,WEI JIE CHEN,et al. A regularization for the projection twin support vector machine[J]. KnowledgeBased Systems,2013:3(37):203210.
[9]QIAOLIN CHUN, XIAZHAO YE, SHANGBING GAO,et al. Weighted twin support vector machines with local information and its application[J].Neural Networks,2012:12(8):3139.
责任编辑(责任编辑:杜能钢)
英文摘要Abstract:This paper researches on the Support Vector Machines training time for long, This paper proposes a twin support vector machine algorithm based on particle warm optimization. Different from the standard support vector machine, The time complexity of the twin support vector machine algorithm based on particle warm optimization is less than the standard support vector machine and it is particularly suitable for uneven data sample classification problems. In particular, having a great advantage for solving largescale data classification problem. In order to verify the validity of the algorithm the paper proposed, Comparison of experimental on text datasets show that twin support vector machine algorithm based on particle swarm optimization is better than the standard support vector machine classifier. Comparison of experimental data on different text datasets show that TWSVM algorithm based on particle swarm optimization and better performance than standard SVM.
英文关键词Key Words: Twin Support Vector Machine(TWSVM);Text Categorization;Particle Swarm Optimization(PSO)

