水下高速直线运动目标的双参考源航迹估计方法研究

王谦，侯宏，尹韶平，陈志菲（.西北工业大学航海学院，陕西西安7007；.中国船舶重工集团公司第705研究所，陕西西安70075；.中国科学院声学研究所，北京0090）



水下高速直线运动目标的双参考源航迹估计方法研究

王谦1，侯宏1，尹韶平2，陈志菲3
（1.西北工业大学航海学院，陕西西安710072；2.中国船舶重工集团公司第705研究所，陕西西安710075；3.中国科学院声学研究所，北京100190）

摘要：针对噪声源识别中水下近场高速直线运动目标的航迹估计问题，将双脉冲源方法扩展到三维空间中。该方法利用公垂线最小化，将基线定位方法估计的两个连续波脉冲参考源的定位结果投影到二维平面内，并结合已知的双参考源间距等信息构造航迹参数的目标函数，进而利用遗传算法估计三维空间内直线运动目标在各脉冲辐射时刻下的位置和航速。仿真结果表明，0 dB条件下当航向角和俯仰角均在［-40°，40°］内时，其估计偏差均在3. 8°以内，而正横距离和深度差的估计偏差在5. 9 m以内。水库实验进一步验证了该方法的有效性。

关键词：声学；参数估计；直线航迹估计；双脉冲源；基线定位

侯宏（1966—），男，教授，博士生导师。E-mail：houhong@ nwpu. edu. cn

0 引言

对水下航行器等高速水下运动目标进行噪声源识别时，需要预估其航迹以便对辐射噪声解多普勒［1 -3］，从而将动态噪声信号还原成静止声源进行处理。精确的航迹估计不仅有利于解多普勒，也便于根据加装在水下航行器上的已知参考源位置，解算噪声源识别结果在水下航行器的对应位置。

在运动目标噪声源识别时，阵列与航迹相距较近，此时多采用时频分析方法或基线定位法估计航迹［4］。对于匀速直线运动目标，其时频曲线参数与航迹参数间有较明确的对应关系，因此时频分析方法，如利用Hough变换提取LOFAR谱图中抛物线参数，或者估计瞬时频率，可以反推航迹信息。时频分析方法仅需要单个阵元，但是信噪比门限较高，非匀速直线运动情况下时频参数的解读较为困难。基线定位方法根据参考源辐射信号到达各阵元的时延差来定位目标，它又分为同步脉冲和异步脉冲定位法。前者需要参考源和接收端的时钟同步到世界标准时间，后者与三子阵法原理相似，通过构造包含目标坐标和辐射时刻的超定方程进行定位［5 -6］。同步脉冲法对时钟要求较高，异步脉冲法降低了硬件要求，但是定位精度相对较差。整体上基线定位方法相对成熟，实际工程中应用广泛。

现有研究大多将水下航行器等运动目标看成分布式点源，在二维平面内作匀速直线运动。而实际中由于测噪船的漂移和水听器阵列的吊放深度等因素，水下航行器航迹与阵列的几何关系需要在三维空间中描述，并且水下航行器实航时是一个加速、匀速到减速的运动过程。文献［7］中双脉冲参考源（DPS）方法通过在目标上加装两个脉冲参考源，增加了双源间距这个条件，从而提高了二维空间中异步脉冲法的定位精度，并且该方法适用于非匀速直线运动目标。本文重新定义了DPS方法中的双源间距（DSS）算子和声程差（PD）算子，并增加公垂线长度（CPL）最小化条件，从而将DPS方法扩展到了三维空间。

1 算法的提出

1. 1 问题的提出

如图1所示，假设阵列位于Oxz平面内，空间直线航迹PQ在Oxy平面的投影PU与x轴的夹角为航向角θ（取值范围（-π/2，π/2）），PQ与PU的夹角为俯仰角φ（取值范围（-π/2，π/2）），PU与y轴交点U的y坐标为正横距离R0（R0＞0），航迹与U点的垂直距离UQ为深度差H0，这样航迹参数（θ，φ，R0，H0）就确定了空间直线航迹。本文假定目标在水下作直线运动，平面阵从测噪船垂直吊放入水，由于测噪船起伏漂移等因素使得航迹与阵列出现图1所示情形。

图1 加装双参考源的直线运动目标Fig. 1 Linear moving target with double reference source

假设目标上有两个间距为r0的同时辐射连续波脉冲信号的参考源A和B，辐射周期均为Tc，载频不同且都位于噪声源识别分析频带以外。对接收信号滤波后可分离两个连续波脉冲信号。对于某个连续波脉冲［8］有

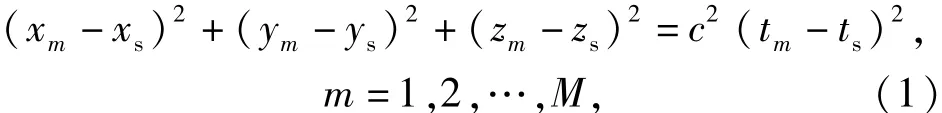
式中：c为声速；M为阵元数。Sm=（xm，ym，zm）和tm分别是第m个阵元的空间坐标和其接收到的脉冲信号前沿到达时刻，（xs，ys，zs）和ts则分别是声源辐射该脉冲时的空间坐标和辐射时刻。（1）式中，xs、ys、zs和ts未知，阵元坐标Sm已知，脉冲前沿到达时刻tm可由接收信号的时域处理得到。当M＞4时，（1）式成为超定方程组，从而可以解得声源坐标（xs，ys，zs）和辐射时刻ts.与文献［7］类似，利用不同时刻下基线定位方法得到的参考源的定向结果和辐射时刻，可以构造目标函数来估计航迹参数（θ，φ，R0，H0）。

1. 2 DPS方法

脉冲基线定位方法的测向精度较高，而测距结果波动较大。DPS方法仅利用其测向结果，使得基线定位结果分布于坐标原点和真实航迹直线所确定的航迹平面内，因此，该拟合平面包含的角度及深度等信息计算结果较为精确。由于基线定位算法的测距精度较差，导致水平定位结果精度较差。本文中DPS方法结合已知的双参考源间距等约束条件来改善其水平定位结果，构造了DSS和PD两个目标函数，并取它们的乘积作为DPS的目标函数来估计航迹参数。

1. 2. 1 将DSS算子扩展到三维空间中

图2中假定Ek和Fk是第k个双脉冲周期下两个参考源的基线定位结果，二维空间内OEk和OFk这两条定向直线与航迹相交，两个交点的间距可直接作为双参考源间距r0的估计值^r0k.三维空间中定向直线OEk与航迹通常是异面直线，同样，OFk和航迹直线也是如此；并且，多个脉冲时刻下估计结果在任意平面的投影点E1、E2、E3…通常不在一条直线上，同样，F1、F2、F3…也如此。为此，图2中取定向直线与航迹间的公垂线在航迹上的垂足Ak和Bk作为Ek和Fk在航迹上的投影点，进而得到双参考源间距估计值^r0k.

以Ak为例，要确定其坐标需要航迹PQ和定向直线OEk的方向向量。由图1的几何关系可得航迹PQ 与Oyz平面交点Q =［0，R0，H0］，那么P点坐标为

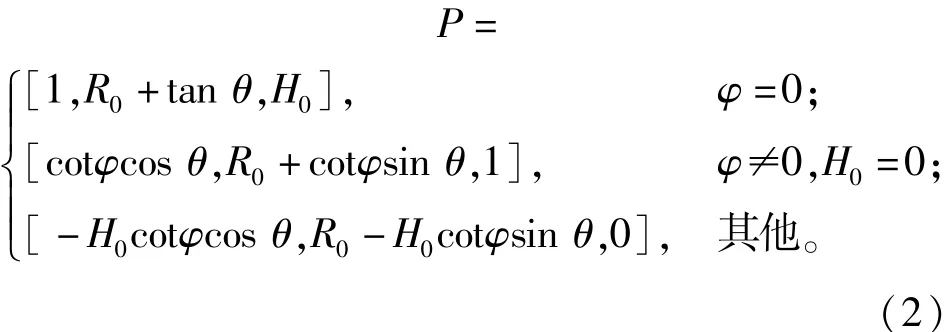
这样航迹PQ的方向向量为

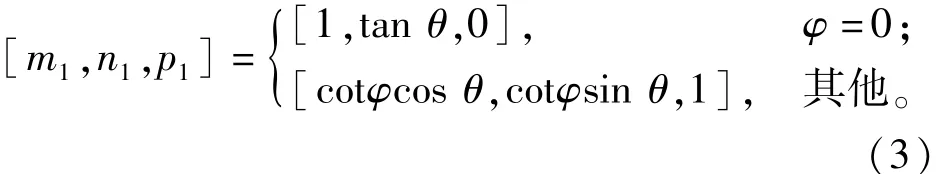
对于第k个双脉冲周期，假设由（1）式估计的脉冲声源坐标为Ek=［xEk，yEk，zEk］，则定向直线OEk的方向向量为

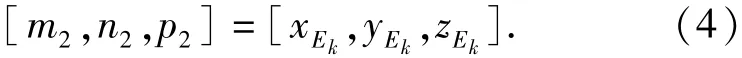
由（3）式和（4）式可得Ak点坐标为

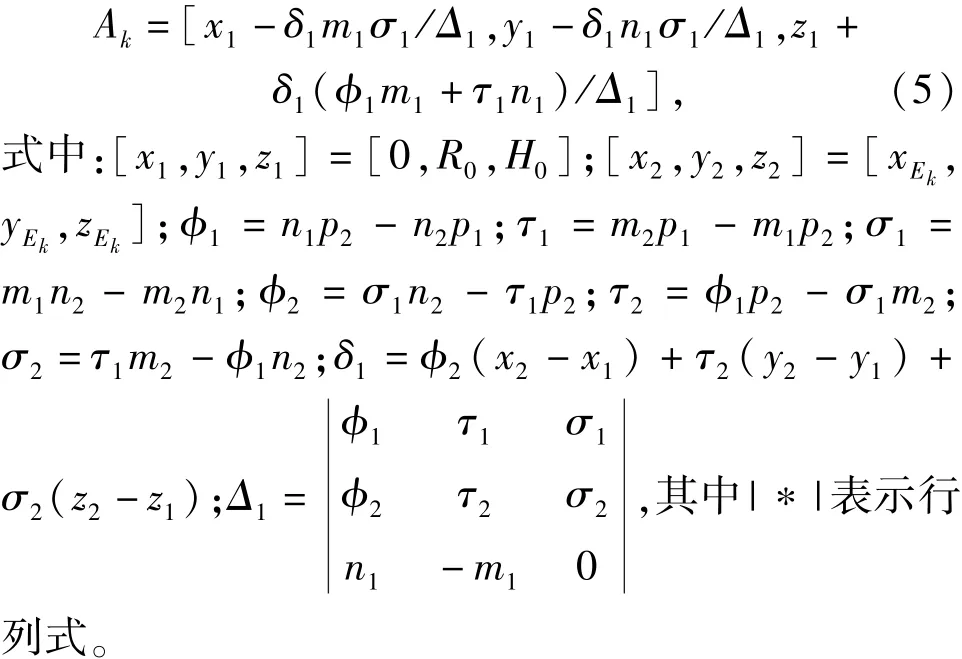
将（4）式中Ek的坐标替换为Fk，即得另一垂足Bk的坐标，因此

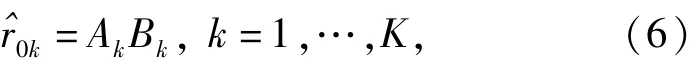
式中：AkBk为Ak和Bk之间的距离，它是航迹参数（θ，φ，R0，H0）的函数；K为双脉冲周期数。显然，通过（6）式可将二维空间的DSS算子扩展到了三维空间，即

1. 2. 2 将PD算子扩展到三维空间中

对于某个频率下的连续波脉冲声源，其相邻两个周期的波形存在图3所示的几何关系。

图3 相邻连续波脉冲的声程差示意图Fig. 3 Schematic diagram of acoustic path difference of adjacent CW pulse

对于坐标为Sm的第m个阵元的接收信号，A声源的相邻两个脉冲波形前沿时刻的差值Tm可由（1）式估计的tm得到，即Tm= tm2- tm1.由此得到相邻脉冲的声程差为

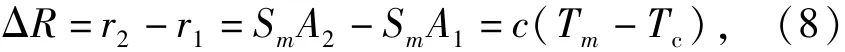
式中：SmA1和SmA2分别是Sm到A1和A2的距离。这里Ak的定义与图2中相同，即定向直线OEk与航迹PQ的公垂线在航迹上的垂足。不同阵元下对每组相邻脉冲均可得到类似（8）式的等式，这样就把PD算子转换到三维空间

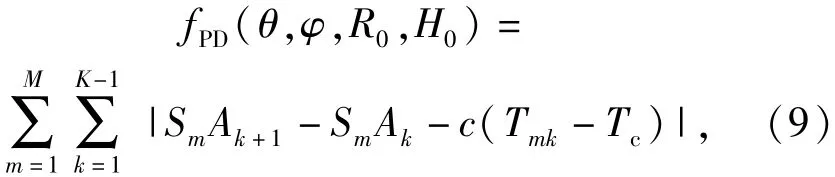
式中：Tmk为第m个阵元接收信号中第k和k + 1个脉冲之间的时间间隔，即Tmk= tm（k +1）- tm（k）.

1. 2. 3 增加CPL最小化的限制条件

在真实航迹所在垂直平面，即图1中的阴影平面内，平行于真实航迹的一些直线对应的DSS和PD算子值较为接近，从而难以确定航迹参数。因此公垂线最小化条件可以规避该情形，即最小化为

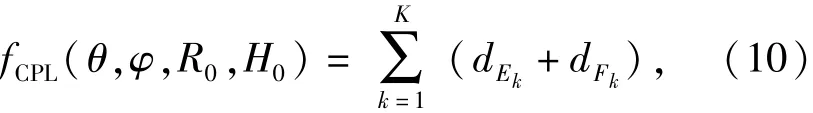
式中：dEk= EkAk，dFk= FkBk，即两条公垂线的长度。其中［9］

上述各变量的定义与（4）式和（5）式中对应变量相同，类似的可以得到dFk的表达式。

1. 2. 4 三维空间的DPS方法

将上述3个算子结合在一起就得到三维空间的DPS方法

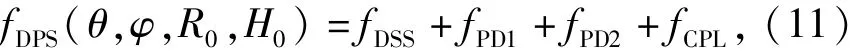
式中：fPD1和fPD2是分别针对两个连续波脉冲声源的PD算子。采用遗传算法使上述目标函数最小化即可得到航迹估计结果。另外，（11）式采用相加而不是文献［7］中相乘的方式得到DPS算子是因为CPL算子的值有可能很小，容易使相乘方式构造的DPS算子出现局部极小值。

为了准确估计相邻脉冲间的目标航速，需要确定各脉冲辐射前沿时刻下双参考源的坐标。以第一参考源为例，其坐标Ak可由航迹估计结果（θ，φ，R0，H0）代入（5）式得到，但是它对应的辐射时刻tE（k）通常不等于（1）式中的ts，因为ts对应的是脉冲基线定位结果Ek的辐射时刻。为此，需要根据各阵元的脉冲前沿到达时刻tEm（k）（m =1，…，M），以及Ak来反推tE（k），即

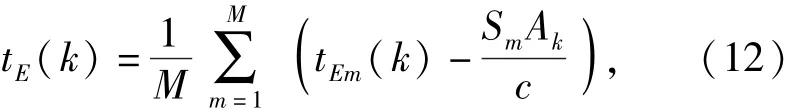
依此方法，可以得到Bk对应的辐射时刻tF（k）.这样相邻两个脉冲信号间目标的航速为

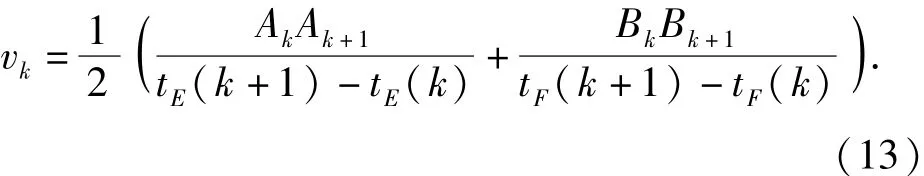
1. 3 理论分析

三维空间的DPS方法相当于将脉冲定位结果对应的定向直线OE和OF投影到平面OPQ上，进而在该平面内利用DSS和PD算子确定航迹参数，因此其核心仍是二维平面内的航迹拟合。在二维投影平面内估计正横距离R＇0和航向角θ＇后，可根据平面OPQ在三维空间的位置得到航迹参数（θ，φ，R0，H0）.

图4给出了双参考源A和B的两组脉冲定位结果投影到平面OPQ后的几何关系。假定目标从左向右作直线运动，r1和r3为第一参考源相邻两个脉冲对应的定向直线，r2和r4为第二参考源相邻两个脉冲对应的定向直线。由基线定向结果可得r1、r2和r3、r4所夹角度分别为β1和β2，它们正对的三角形边长均为双源间距r0.

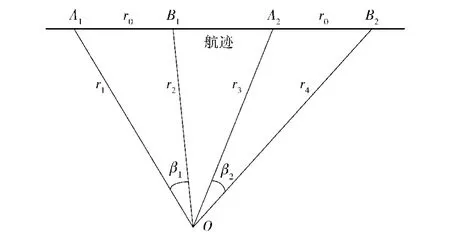
图4 DPS方法原理示意图Fig. 4 Schematic diagram of DPS method

由三角形三边关系有

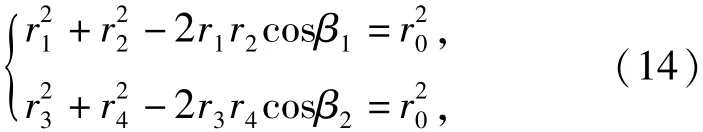
式中：r1、r2、r3、r4为未知量。若以三角形OA1B1为参考，OA2B2的对应边长和夹角可改写为r3= r1+Δa，r4= r2+Δb，β2=β1+Δβ，其中Δa、Δb分别为同一参考源在不同位置的距离估计差，Δβ为两次估计夹角的差，代入（14）式得

整理得

当有多组双脉冲定向结果时，即有多个三角形OAiBi，i =1，…，K，可利用（16）式构建r1和r2的二元二次方程组

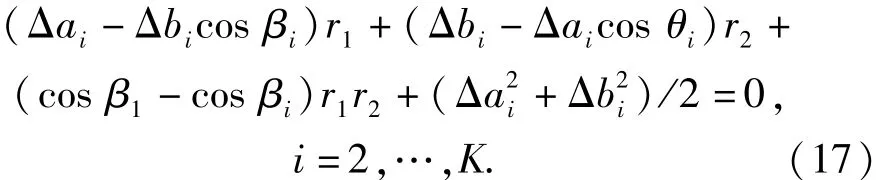
二维空间内DPS方法就是要寻找一条航迹直线与rk所在的定向直线相交，并尽可能保证AkBk= r0.而对于任意给定的航迹直线，（17）式中独立的未知量仅有r1和r2.

当K =4时，通过简单的变量代换可得

式中：Ui=Δai-Δbicos βi；Vi=Δbi-Δaicos βi；Wi=cos β0- cos βi；Xi=（Δa+Δb）/2.

（18）式、（19）式成立的条件是分母不为0，整理后得Wi/ Wj≠Ui/ Uj，Wi/ Wj≠Vi/ Vj，其中i≠j，这在实际中容易满足。尤其是当K＞4时，可采用非线性最小二乘求解（17）式得到r1和r2，从而得到二维空间航迹参数（θ＇，R＇0），并换算到三维空间中的（θ，φ，R0，H0）.

2 仿真

本文着重给出不同信噪比下，以及不同航向角和俯仰角下DPS方法在三维空间中的航迹参数估计性能。在图1所示条件下，假定采用M = 9元均匀十字阵，其中垂直方向阵元数为2个，阵元间距d =0. 3 m.两个间距r0= 0. 5 m的连续波脉冲声源载频f0=［6 000 Hz，7 000 Hz］，脉冲周期均为Tc= 200 ms.水中声速c = 1 500 m/ s，目标作航速υ= 20 m/ s的匀速直线运动，航迹参数（θ，φ，R0，H0）= ［10°，15°，40 m，0 m］，从中截取K =7组双脉冲进行航迹参数估计。图5给出了信噪比SNR =0 dB时的航迹估计结果，其中信噪比定义为双脉冲源的能量和与背景噪声能量的比值，基线定位方法是第一参考源定位结果则经过了Kalman平滑处理。图5 中DPS估计的航迹参数为（θ，φ，R0，H0）= ［10. 42°，15. 07°，39. 17 m，- 0. 01 m］，即估计偏差为［0. 42°，0. 07°，0. 83 m，0. 01 m］.

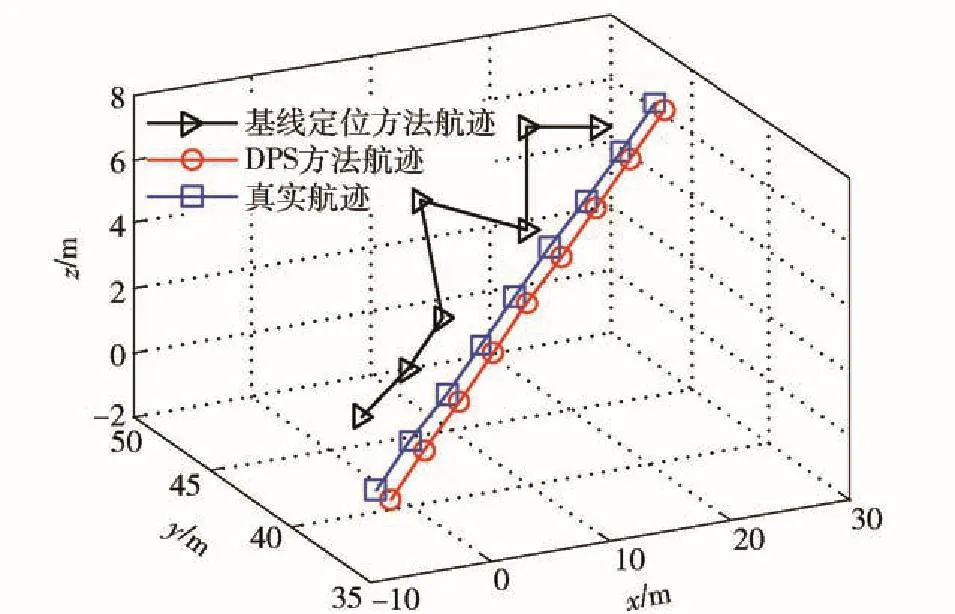
图5 0 dB时DPS方法的航迹估计结果Fig. 5 Track estimation result of DPS method at 0 dB

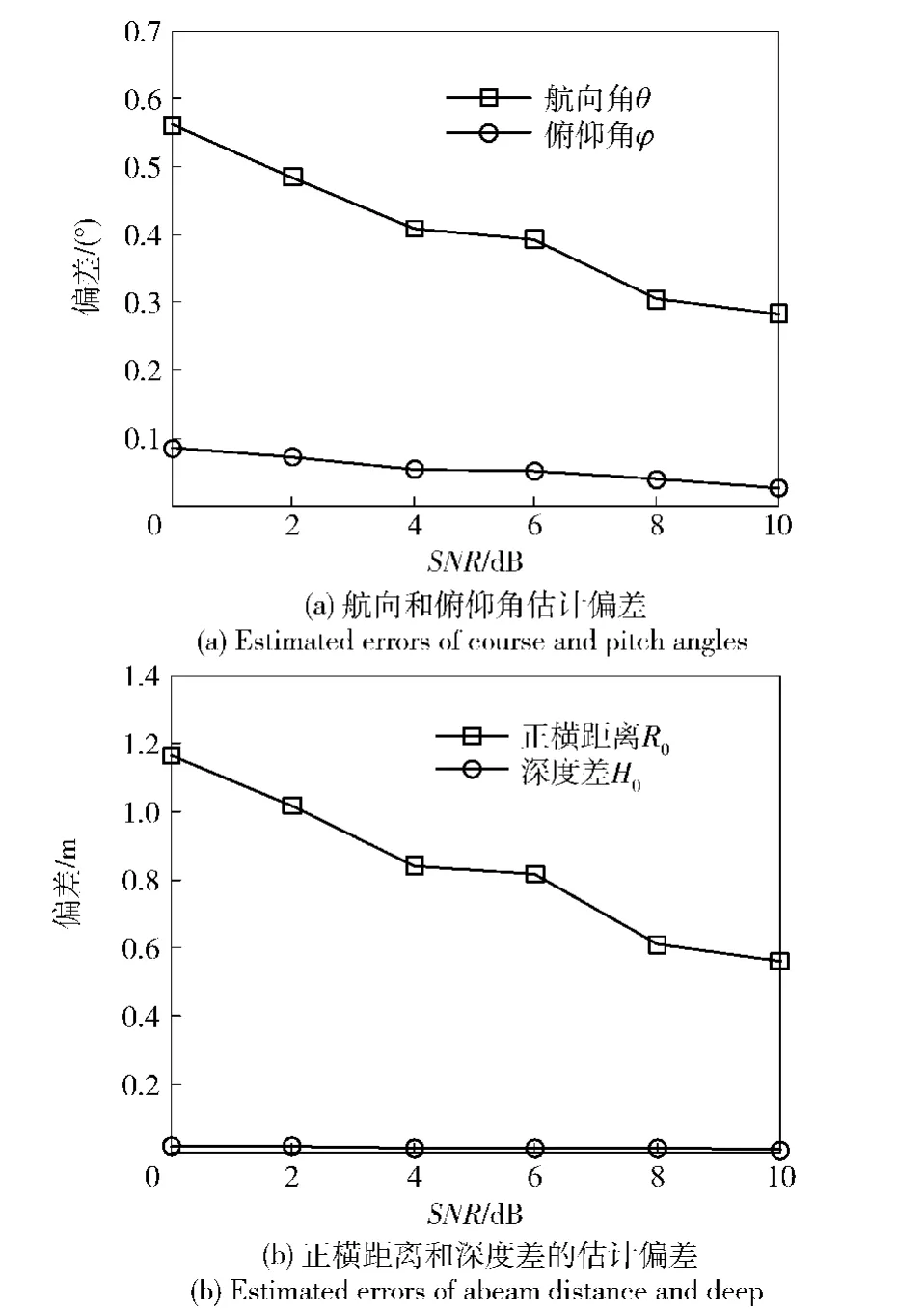
图6 不同信噪比下DPS方法的航迹参数估计性能Fig. 6 Track estimation performance of DPS method at different SNRs

相同仿真条件下，图6给出了100次Monte Carlo实验后，不同信噪比下DPS方法的航迹参数估计结果的平均绝对偏差。随着信噪比的提高，DPS方法的航迹估计性能不断提高，其中航向角θ和正横距离R0的估计偏差大于俯仰角φ和深度差H0的估计偏差。这与平面阵对垂直于其所在平面的纵深方向的分辨能力较弱有关，因而航向角θ和正横距离R0也更易受到基线定位方法测向偏差，以及声程差估计偏差的影响。图7和图8分别给出了0 dB下100次Monte Carlo实验后不同航向角和俯仰角下航迹参数的平均估计偏差，其中航向角θ和正横距离R0的估计偏差仍大于相应的俯仰角φ和深度差H0的估计偏差。另一方面，随着航向角θ和俯仰角φ的增大，即航迹直线与平面阵所在平面夹角增大时，航迹估计性能逐渐下降。在0 dB下，当航向角θ和俯仰角φ均在［-40°，40°］内时，θ和φ的估计偏差在3. 8°以内，而R0和H0的估计偏差在5. 9 m以内。

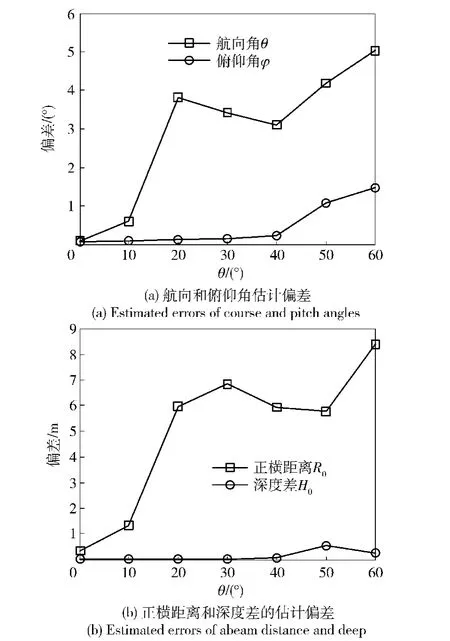
图7 不同航向角下DPS方法的航迹估计性能Fig. 7 Track estimation performance of DPS method at different course angles

3 水库实验验证

受限于实验成本，下面以水库中自由落体目标的航迹估计为例来验证DPS方法。图9给出了实验示意图，其中水听器阵列与运动目标均在垂直面内，即（θ，R0）确定了航迹。水听器阵列为6 m长的11元均匀十字阵，其中垂直方向阵元数为2个。运动目标为从水面开始作自由落体的金属壳体，其上加装两个间距r0= 0. 4 m的脉冲参考源，连续波脉冲载频为［7 000 Hz，10 000 Hz］，脉冲周期均为200 ms.

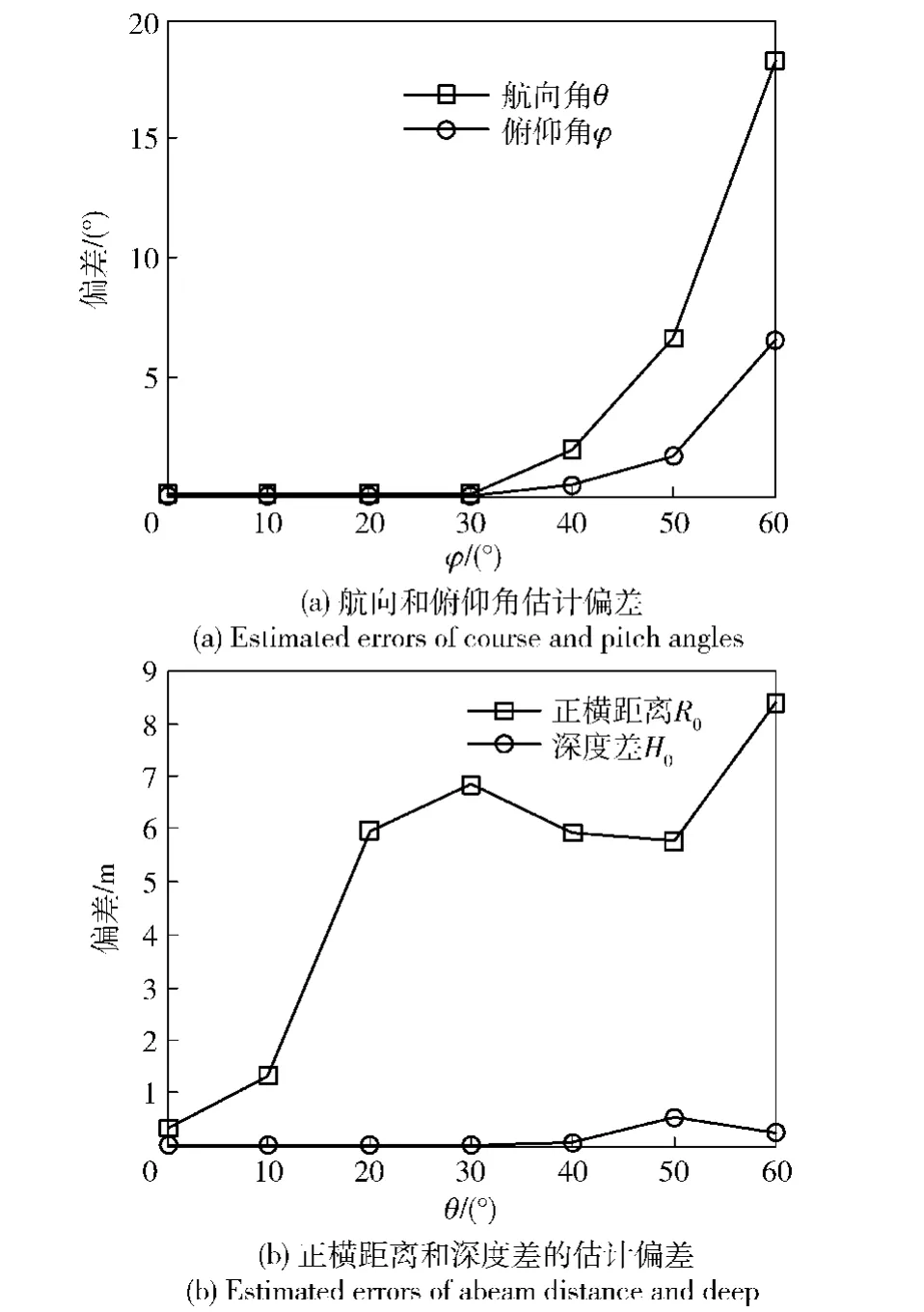
图8 不同俯仰角下DPS方法的航迹估计性能Fig. 8 Track estimation performance of DPS method at different pitch angles

图10给出了两次独立实验的航迹估计结果。两次实验中仅改变了阵列与航迹的间距R0，其他实验参数和环境相同。两次实验的真实航迹参数（θ，R0）分别为（0°，31. 3 m）和（0°，23 m）。DPS方法的航迹估计结果分别为（- 5. 7°，32. 5 m）和（-5. 1°，21. 2 m），即正横距离R0估计偏差在2 m以内，航向角θ估计偏差在- 6°以内。航向角估计偏差过大可能是由于锚定的浮船仍在水面上缓慢旋转漂移，使得垂直吊放的线阵有一定倾斜度，因此上述实验中真实航向角可能在-5°左右。

4 结论

本文在文献［7］的双参考源航迹估计方法基础上，将原有的双源间距和声程差目标函数扩展到三维空间，并引入CPL最小化目标函数，从而将二维空间中的DPS方法推广到了三维空间中。DPS方法相当于利用三维空间中基线定位方法的定向结果，以及已知的双参考源间距等信息构造航迹参数的最优化目标函数，进而通过遗传算法估计近场直线运动目标航迹。所得到的航迹信息包含各脉冲辐射时刻下目标的三维坐标，因而也可以得到各时段下直线运动目标的航速。仿真和水库实验验证了DPS方法的有效性。

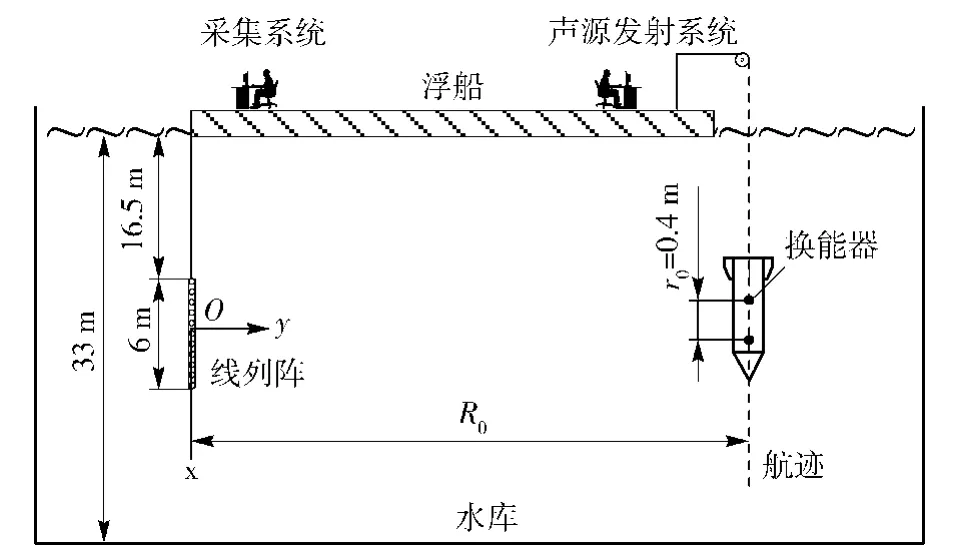
图9 水库航迹估计实验示意图Fig. 9 Schematic diagram of track estimation test in reservoir

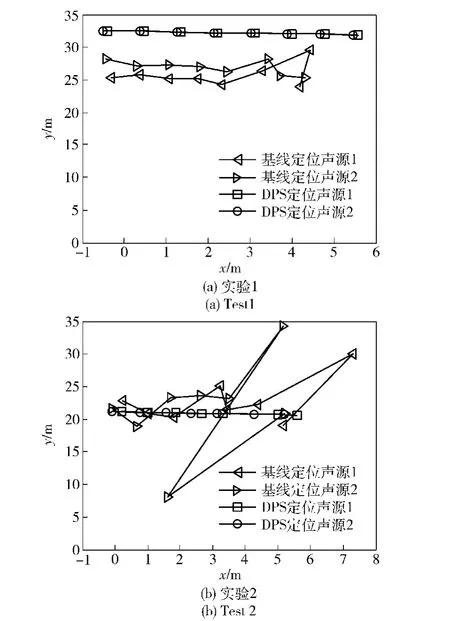
图10 两次水库实验的航迹估计结果Fig. 10 Two result of track estimation test in reservoir

参考文献（References）

［1］ Kim S M，Choi Y，Lim Y K. Nearfield noise identification with a passive array in the underwater anechoic basin at KRISO［C］∥OCEANS 2003. San Diego，CA，US：IEEE，2003：1389 -1394.

［2］ Yoon J H，Kim D Y，Bae S H，et al. Joint initialization and tracking of multiple moving objects using Doppler information［J］. IEEE Transactions on Signal Processing，2011，59（7）：3447 -3452.

［3］ Tegborg V，Pettersson M I，Claesson I. Experimental results of passive imaging of moving continuous broadband sound sources within a sensor field［J］. IEEE Journal of Oceanic Engineering，2011，36（1）：25 -36.

［4］ 董利英，陈志菲.近场条件下脉冲基线定位性能影响因素分析［J］.鱼雷技术，2014，22（2）：100 -104. DONG Li-ying，CHEN Zhi-fei. Influencing factors of pulse baseline positioning performance in near field［J］. Torpedo Technology，2014，22（2）：100 -104.（in Chinese）

［5］ Hu B，Yang D，Shi S，et al. Underwater moving noise source identification based on hybrid near-field acoustical holography ［J］. Science China：Physics，Mechanics and Astronomy，2011，54（9）：1570 -1578.

［6］ Mei J D，Sheng X L，Guo L X，et al. Sea trial research on multisource underwater acoustic image measurement technology based on the sparse array［C］∥OCEANS 2010. Seattle，WA：IEEE，2010.

［7］ Chen Z，Hou H，Yang J，et al. Linear track estimation using double pulse sources for near-field underwater moving target［J］. Journal of Marine Science and Application，2013，12（2）：240 -244.

［8］ 陈晓忠，梁国龙，王逸林，等.非同步水声定位技术及其性能评价［J］.声学学报，2003，28（4）：357 -362. CHEN Xiao-zhong，LIANG Guo-long，WANG Yi-lin，et al. Nonsynchronous underwater acoustic location and it’s performance evaluation［J］. Acta Acustica，2003，28（4）：357 - 362.（in Chinese）

［9］ 董玉久，潘秀英，杨欣欣.两异面直线公垂线垂足位置的计算方法［J］.哈尔滨科学技术大学学报，1990，14（1）：84 -88. DONG Yu-jiu，PAN Xiu-ying，YANG Xin-xin. A calculation method for finding the foot of common perpendicular of lines on different places［J］. Journal of Harbin University of Science & Technology，1990，14（1）：84 -88.（in Chinese）

Research on Double Reference Source Estimation Method for 3-dimension Space of Near-field Underwater Moving Target with Linear Track

WANG Qian1，HOU Hong1，YIN Shao-ping2，CHEN Zhi-fei3
（1. School of Marine Science and Technology，Northwestern Polytechnical University，Xi’an 710072，Shaanxi，China；2. The 705 Research Institute，China Shipbuilding Industry Corporation，Xi’an 710075，Shaanxi，China；3. Institute of Acoustics，Chinese Academy of Sciences，Beijing 100190，China）

Abstract：For the identification of noise source，the track information could be applied to Doppler compensation for the recorded noise emitted from moving vehicle. Linear track estimation of near-field underwater moving target by double pulse source（DPS）has been used successfully in 2-dimension. The use of DPS is extended to 3- dimension space in order to linearly track the target. The positioning result of double reference source obtained by the baseline positioning method is projected to a certain plane under the limitation of common perpendicular minimum length. The objective function of DPS is constructed with the known distance of double reference source. The track information in 3-dimension space is obtained by using genetic algorithm. The simulation results show that the estimated errors of azimuth and pitch angles are less than 3. 8°when their trace line lies under［-40°，40°］in case of 0 dB noise level. The estimated errors of abeam distance and depth difference are kept less than 5. 9 m at the same time.

Key words：acoustics；parameter estimation；linear track estimation；double reference source；baseline positioning

中图分类号：TB568

文献标志码：A

文章编号：1000-1093（2016）04-0677-07

DOI：10. 3969/ j. issn. 1000-1093. 2016. 04. 015

收稿日期：2015-05-20

基金项目：海军装备预先研究项目（4011003010201）

作者简介：王谦（1982—），男，高级工程师，博士研究生。E-mail：king2397@126. com；