一年级小学生的函数概括能力分析

裘陆勤

(逸夫小学，浙江嵊州 312400)

一、问题的提出

所谓函数思想，是指通过提出问题的数学特征，建立函数关系型的数学模型，从而进行研究。而简单函数概括能力是指用函数的概念和性质去分析问题、转化问题和解决问题的思维策略。在小学数学中并不学习函数的概念，大部分教师也认为低年级的小学生是没有函数概括能力的。那么，小学生在看到具有函数关系的算式时，到底用怎样的解题策略来计算，能否发现算式之间的联系呢？为回答这个问题，本文设计了实验，考察一年级的小学生是否具有初步的函数思想。方法是给出不同类型的加法口算题，让小学生回答“你是怎么计算的？”从学生的思考方式中分析他们是否具有简单的函数思想和分析概括能力，为小学数学教学设计提供基础。

二、研究目的及主要问题

1.研究目的

分析一年级的学生是否具有简单的函数思想和函数概括能力，为小学数学教学提供参考依据。

2.研究的主要问题

(1)一年级的小学生能否独立地发现各类题组的运算规律；

(2)一年级的小学生能否用语言表述运算规律；

(3)一年级的小学生能否将解决前一类型题组所用的规律性的东西(函数关系)迁移到解决后一类型题组中去。

三、研究设计

1.研究对象

按照现行的小学数学教材[1]，我们选择了不同教师任教的一年级6个班，共240名学生。他们均已学习过10以内加减法。

2.测试和访谈题目

本次测试我们主要用加法算式组成四种不同类型的题组，每个题组均为竖排，同一类型的题分6组，每组6道算式。

A型题组：

B型题组:

C型题组:

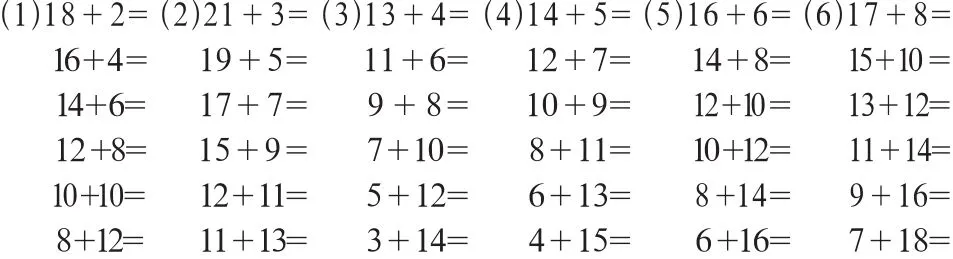
D型题组：

3.测试和访谈过程

测试时间选择在2015年6月，测试对象为不同教师任教的一年级6个班共240名学生。

为了保证测试的有效性，测试前我们没有给学生任何的解题提示，也没有任何讨论与交流。整个测试过程基本反映了学生独立地在自然情景下的简单函数概括能力水平。

测试时，主试老师先向学生依次出示A型题组的各组题目(一张小卡片)，并对他说：“你先看看，这张小卡片的6道题之间有什么关系，想一想再做。”在学生做题的过程中，主试老师仔细观察他的计算过程，并随时询问：“你是用什么方法做这些题的？”每当学生做完一组题后之后，主试老师就要询问他的做题方法，看他需要经过几组题的运算，才能发现A组题的运算结果是随着一个已知加数的变化而有规律地变化，而不必再逐个算式计算。然后要求学生表达这种变化规律，主试老师记下他的回答。

当学生发现A型题组的函数关系并能用语言表述之后，方可转入B型题组；发现B型题组的函数关系，并能用语言表述之后，方可转入C型题组；发现C型题组的函数并能用语言表述之后，方可转入D型题组。

如果在同一类型的题组连续做6组之后，学生仍然不能发现该题组的函数关系，就定为不能发现规律者。对不能发现规律的学生，主试老师可提供帮助，告诉该题型的函数关系，直到该生按老师所讲的规律写出得数，并能复述其规律方可转入下一类型题组。如果经主试老师的帮助仍不能发现规律和表达规律的学生，就不再做下一组类型的题目。

4.测试的评价

为了能将学生在测试和访谈中的思维方式量化出来，我设定了统一评分标准：

(1)每种类型题组发现规律的水平分为七级。凡不需要计算立即发现规律者得7分，以下按能者所需要题组的数目逐减1分(如需要1个题组得6分；需要2个题组得5分……)，经6组题的计算不能发现规律者为0分。

(2)每种类型题组的言语表达水平分五级(A级表述概括、清楚，B级表述具体、清楚，C级表述概括、比较清楚，D级表述具体、比较清楚，E级表述不清楚)，凡表述水平为A者得5分，随表述水平逐级下降连续减1分，不能表述者得0分。

评价等级划分：

48～39分为优秀，38～28分为中上，27～18分为中，17～8分为中下，8分以下为差。

四、简单函数概念的测试结果分析

1.近80%的一年级学生已经具备了简单函数概括能力和知识迁移能力。

表1 一年级学生函数关系概括能力的评价

从上表中我们可以看出，79.6%的一年级学生已经能独立地发现各类题组的运算规律，清楚地用数学语言或具体的表述概括每组的函数规律，并且能将解决前一类型题组所用的规律性的东西(函数关系)迁移到解决后一类型题组中去。如小黄同学在做A型口算题组时，他只是纯粹的口算，不知道除了口算还需要观察和思考什么；当他完成A型同一类型的6组口算后，我引导他观察每组6道口算中的第1个加数、第2个加数、和是如何变化的，并让他自己复述A型题组的函数关系；当他进入B型题组、C型题组、D型题组后就能从第1个加数、第2个加数、和这三个角度去思考该型题组中的函数关系了，可见他已经具备了知识迁移能力和简单的函数概括能力。

2.定势思维促使一年级学生见到口算题就口算，而且加数变化的个数直接影响着学生是否运用函数关系解题。

从表2可知，一年级学生见到A型口算题组的第一反应就是口算，这也可能与平时的口算练习有关。当学生经历A组有规律的口算题后，他们自然地把解决A型题组的规律性东西(函数关系)迁移到解决B型题组中，所以部分学生在发现B型题组规律时出现了“第一个加数一个一个变小，第二个加数不变，和一个一个变小”的负迁移。此时学生面对的是只有一个加数在变化，而另一个加数不变，所以70%以上的学生能直接说出结果的变化规律。

表2 一年级学生函数关系概括中口算的比例

当他们遇见C型题组这样的“熟悉的陌生人”(说熟悉是因为学生知道要关注第一个加数、第二个加数以及和的变化；说陌生是因为学生面对的是两个加数都在变化)时，大部分学生都选择了用口算的方式来发现和的变化规律，只有少部分学生用“一个数少2，另一个多2，和不变”的守恒规律来运算。

D型题组是对C型题组的深入，两个加数不仅都在变化，而且变化的趋势也不同，给学生判断和的变化趋势带来了一定的干扰因素。这也是大部分学生选择用口算的方式来发现和的变化规律的主要原因。

3.多数学生已经能用儿童化的数学语言清楚、概括地描述每种类型的函数关系。

由表3可以看出，一年级的学生已经能用数学语言清楚地描述每种类型的函数关系，如他们把加号前面的数称为加数1、第1个加数、左边的数、第1列等；加号后面的数称为加数2、第2个加数、右边的数、第2列；等于号后面的数称为和、答案、结果等；变化趋势用不变、几个几个变大、几个几个往后数、几个几个加上去，几个几个变小、几个几个往前数、几个几个减下来、相差几个等来表述。

表3 一年级学生函数关系概括中言语表达的主要方式

4.观察视角、口算水平和迁移水平限制着学生的函数关系概括能力。

在测试后，我们对不能概括这些题组函数关系的学生进行了分析，发现观察视角、口算水平和迁移水平这三大因素限制着他们的简单函数概括能力。

从观察视角方面来看，他们在测试过程中出现了只会横项看或纵向观察不一致等现象。如小胡同学在观察A型第1组的6道口算时，发现了“5比4大1，6比4大2，7比4大3……”这样的规律，直到观察完A型6组题目仍不能发现规律，成功复述A型题组规律后进入B型题组，她仍然只会看横项来概括该组的函数关系。如小邱同学只用加法的形式来表述，如C型题组的函数关系是“加数1从下往上依次加2，加数2从上往下依次加2，和不变”，D型题组的函数关系是“加数1从上往下依次加2，加数2从下往上依次加3，和从下往上依次加1”。如小周同学的观察视角不一致，如A型题组的函数关系是“第1列不变，第2列是10、9…5，和一个一个变小”。

从口算水平方面来看，我们发现等级是中上、中和中下的学生也能发现第1个加数、第2个加数的变化规律，但是他们由于口算能力较差对于结果的判断出现了错误。如小陈同学得到B型题组的函数关系是“第1个加数两个两个变小，第2个加数不变，和一个一个变小”。

从迁移水平方面来看，个别学生还不具备复述规律或者不能把前一题的规律迁移到下一题中去的现象。如小许同学在经历A型6组口算后仍然不能发现该组的函数关系，虽然在给他提供帮助时他认可这样的思考方式，但是他不能按要求独立复述这样的函数关系。小陈同学虽然能独立复述A型题组的函数关系，但是当进入B型题组时仍然不能正确说出该组的函数关系。

5.个别学生不仅关注了函数关系，还关注了单双数的运算性质。

我们在测试中发现对于同样的测试题，个别学生具有多元思维方式。如小林同学在观察A型第1组时不但说出了“第1个加数不变，第2个加数一个一个变大，和一个一个变大”，还概括出“双数加上双数是双数”“双数加上单数是单数”；在观察第2组时既概括出函数关系，还总结出“单数加上单数是双数”的结论。

结 语

从上面这组题目的测试和分析中，我们可以得到以下结论：

1.大部分一年级学生已经具备了简单的函数概括能力，能够用儿童化的数学语言清晰、概括地描述各种类型的函数关系；

2.学生的简单函数概括能力具有差异性，有的学生能发现题组中的函数关系和其他运算性质；有的学生却还不具备简单函数概括能力；

3.定势思维、观察视角、口算水平和迁移水平等因素限制着个别学生的函数关系概括能力。

上面的结论对小学数学教学有以下启示：

1.在平时教学中要注重培养学生的函数概括能力，渗透函数思想，并加强学生的数感训练；

2.在学生机械模仿的基础上，要重视对学生迁移能力、求异思维和变通性等能力的培养；

3.解决同一个数学问题，对于同一年龄段的学生来说，他们的思维方式既有共性又有个性；

4.作为教师，必须了解学生的学习水平，知道学生的学习能力，因材施教。

[1] 张天孝.小学新思维数学研究[M].杭州:浙江大学出版社,2011：30-43.