四元Heisenberg群上的链和R-圆及其性质

施云

（浙江大学数学科学学院，浙江杭州310027）



四元Heisenberg群上的链和R-圆及其性质

施云

（浙江大学数学科学学院，浙江杭州310027）

定义了四元双曲空间上的链和R-圆，并给出了链在垂直投影下的性质.证明了经过Heisenberg群上固定两点的链的唯一性，R-球的qc-水平性，并给出了R-圆与纯虚R-圆之间的关系.

四元双曲空间；四元Heisenberg群；链；R-圆

§1　引　言

近年来，四元切触几何有许多深入系统的研究和应用，参见［1-11］等.四元切触几何是多复变中CR几何的四元对应物.四元Heisenberg群和四元双曲空间是研究四元切触几何的最简单的模型.［9］中介绍了复双曲空间HnC的球模型和Siegel域模型，并给出了HnC上的链和R-圆的定义及其性质.在［12］中，Jacobowitz给出了链和R-圆的等价定义并用其他方法得出了类似的性质.本文介绍了四元双曲空间，四元Heisenberg群，Siegel域，并对四元Heisenberg群上的链和R-圆进行了一些研究. Cartan证明了与Von Staudt定理相类似的链保持定理（参见［9］p.136），在复的情况下，R-圆被应用于PU（n，1）的离散子群的研究（参见［9］p.149）.我们期望四元情况下也有类似的链保持定理，R-圆也能被应用于PSp（n，1）的离散子群的研究.

§2回顾了四元双曲空间的基本定义，Heisenberg群H上的自同态（参见［13］p.81）以及四元Heisenberg群与Siegel域之间的关系（参见［6］p.145）.§3引入了四元双曲空间上的链的定义，给出了有限链和垂直链在垂直投影下与Hn-1的关系，证明了经过Heisenberg群上两点的链的存在唯一性以及经过Heisenberg群上一点与垂直切空间上一点相切的链的存在唯一性.§4引入了四元双曲空间下的R-球和R-圆，定义了纯虚R-圆，证明了任何R-球均是qc-水平的子流形以及任何一个R-圆可以看成是由纯虚R-圆在Heisenberg作用下变换而得.

§2　预备知识

四元切触流形（M，g，Q）是由一个（4n - 1）-维流形（n≥2）M和一个余维数为三的分布H构成的，局部的，H可以表示成一个R3-值的1-形式Θ=（θ1，θ2，θ3）的核，称H为水平空间，g是其上的度量.进一步地，H有Sp（n）Sp（1）-结构，即其上配有秩为3的丛:

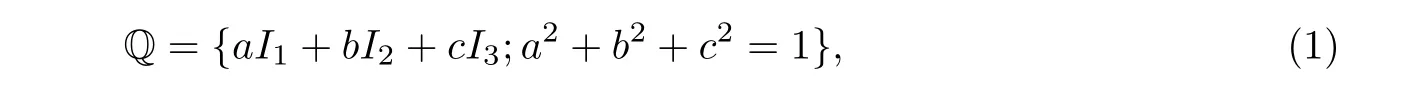
其中殆复结构I1，I2，I3是H上的自同态，局部的，满足四元交换律:

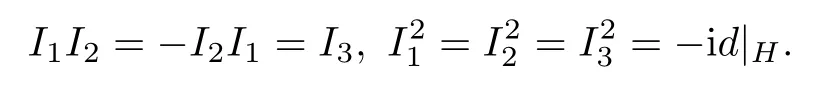
它们与度量Hermitian相容:

且对于任意的X，Y∈H，s = 1，2，3满足相容条件

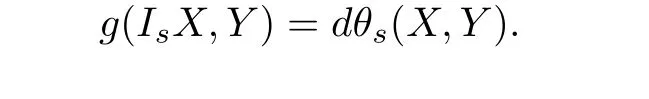
记I :=（I1，I2，I3）.

四元Heisenberg群H = Hn-1⊕R3上有乘法

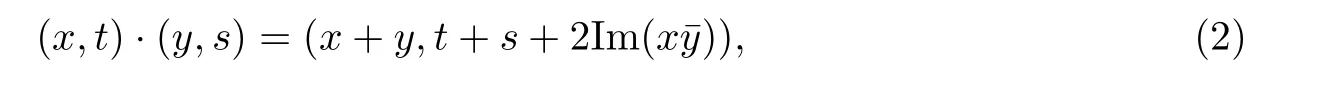
其中，x =（x1，···，xn-1），y =（y1，···，yn-1），t =（t1，t2，t3），s =（s1，s2，s3），x¯y = x1¯y1+···+ xn-1¯yn-1，且它的原点是e =（0，0）.对于任意的ξ=（x，t），定义它的模为

H上有如下自同态（参见［13］p.81）:

（1）胀缩:

（2）左平移:

（3）旋转:

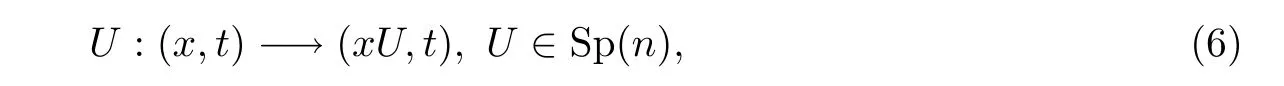
其中

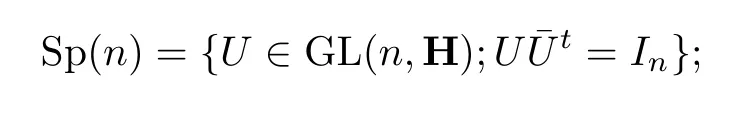
（4）反射:

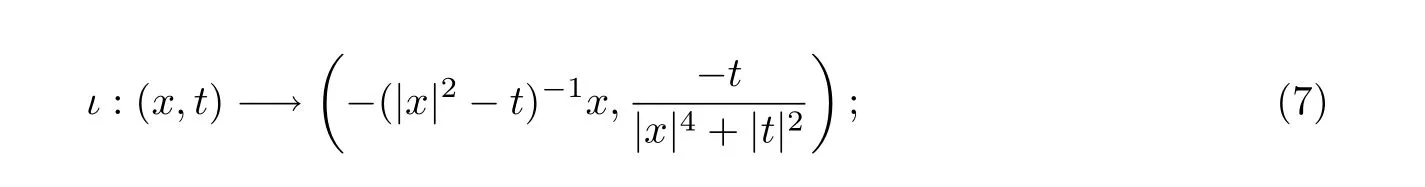
（5）Sp（1）的作用:

其中在第一个因子上的作用是左乘σ∈H且|σ| = 1，在第二个因子上的作用与SO（3）同构.

（6）共轭:

把（4）-（9）式中若干映射的复合称为Heisenberg作用.

令（M，g，Q）为一个四元流形，称它的一个k-维子流形S∈M为水平的，当且仅当它处处切于H，即对于任意的s∈S，它的切空间TsS∈Hs.

四元Heisenberg群H的乘法写成实变量的形式可以表示成

其中s = 1，2，3，y =（y1，y2，···，y4n-4），y′=（y′1，y′2，···，y′4n-4）∈R4n-4，t =（t1，t2，t3），t′= （t′1，t′2，t′3）∈R3（参见［8］（2.15））.四元Heisnberg群H上的左不变向量场可以表示成

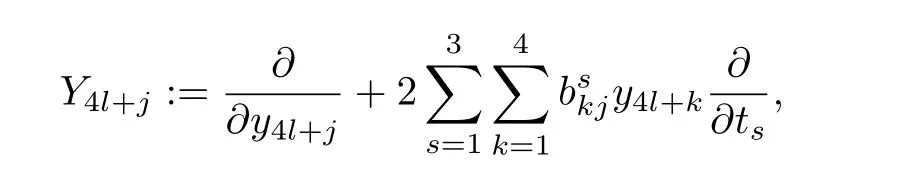
l = 0，···，n - 2，j = 1，···，4（参见［8］（2.17））.

四元Heisenberg群的水平子空间HH:= span｛Y1，···，Y4n-4｝.

令Hn，1为一个（n + 1）-维四元线性空间，它包含

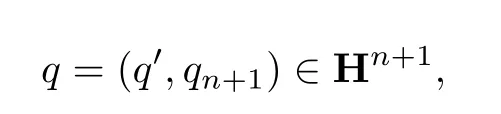
其中q′=（q1，···，qn）∈Hn，qn+1∈H.在Hn，1上定义内积

n-维四元射影空间P（Hn+1）是Hn+1中左四元直线的集合.精确的

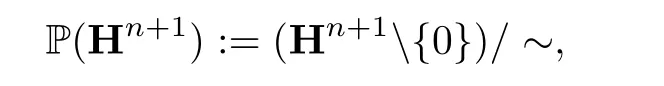
其中～是等价关系:如果（p′1，···，p′n+1）～（q′1，···，q′n+1）∈Hn+1，则存在非零四元数λ使得

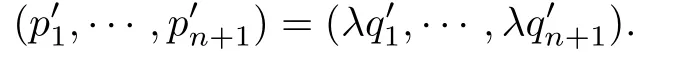
称向量Q∈Hn，1为负（零，正），当且仅当＜0（ = 0，＞0）.直线l∈Hn，1称为负（零，正），当且仅当l由负（零，正）向量组成. P（Hn，1）的包含Hn，1中的负直线的子集称为n维四元双曲空间，记为HnH.

P（Hn+1）在Sp（n，1）的诱导作用下，存在三个不变子空间

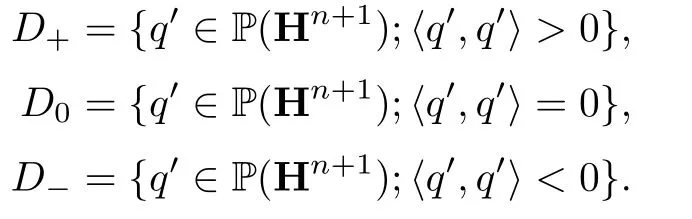
作为Sp（n，1）的齐性空间，D-等价于四元双曲空间HnH. HnH中的点的稳定子是Sp（n，1）的最大紧子群，记为Sp（n）×Sp（1）（参见［14］p.524）. Sp（n，1）是保持<·，·>的（n + 1）×（n + 1）四元数矩阵. 在Hn上定义内积

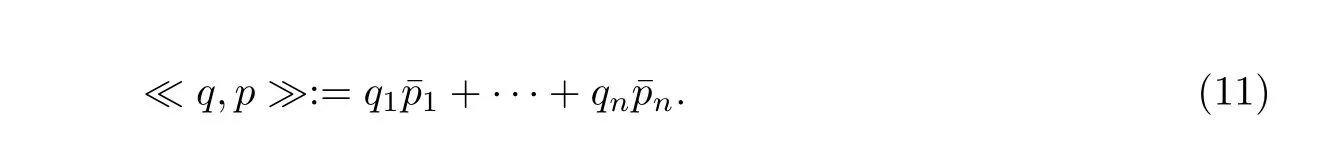
Sp（n）保持≪·，·≫不变.

取q∈∂HnH，与其相应的零线由零向量Q∈Hn，1生成.存在唯一的与∂H相切于q的H-超平面H（q），与之相应的线性超平面是）上与H（q）互补且包含的仿射片是一个无界区域.可以把嵌入映射表示为，令Q为向量

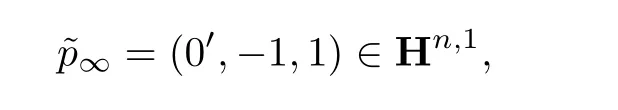
对应于球模型的南极，其中0′=（0，···，0）∈Hn-1，因此H（˜p∞）由所有

表示的点组成，其中q =（q1，···，qn-1）.

映射

是所需的仿射嵌入.

（1）球模型

可以把HnH和单位球

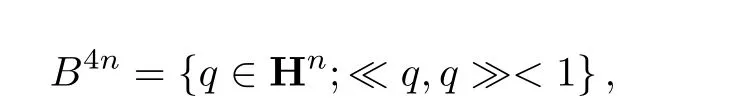
通过如下映射等同起来.令

为把Hn嵌入到P（Hn，1）的映射（在齐性坐标下qn+1/= 0）.由于当qn+1= 0时，Hn，1中的向量是正的，故有HnH⊂A（Hn），且A把B4n和HnH，以及∂B4n= S4n-1⊂Hn和∂HnH等同起来.

（2）Siegel域模型

四元双曲空间HnH还可以等同于一个无界域，即Siegel域

通过Cayley变换:

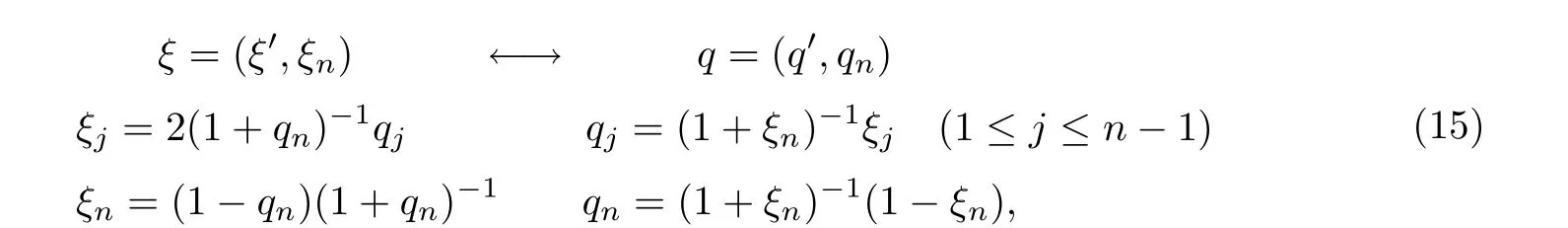
等同起来（参见［6］p.145）.

反射ι把原点映到∞，如果Dδ是原点处的一个涨缩，那么

令E为四元向量空间.如果数量乘法只考虑R∈H，则存在实向量空间ER，称为E下的实向量空间.定义ER上的关于I1，I2，I3不变，非退化的双线性形式

子空间S⊂ER称为全实的当且仅当S，I1S，I2S，I3S在（（，））下垂直.

流形M的一个子流形N称为在x处是全测地的，如果对于任意的X∈TxN，M上由x和X定义的测地线也是N上的测地线.如果对于N上的所有点N都是全测地的，则称N为M的全测地子流形.如果N⊂M既是全实的又是M的全测地子流形，则称N为全实全测地子流形.

§3　链

四元Heisenberg群上的链起到的作用与Riemann几何上测地线起到的作用类似.与复的情况相类似，对于任意的x∈B4n，存在g∈Sp（n，1）把x映射到球心e，令F′⊂TeBn为过球心的一个k-维四元线性子空间，存在唯一的一个过球心且与F′相切的全测地子流形.记g（F′）= F.由于g是等距的，通过g-1可得唯一的包含x且与F相切的全测地子流形.把这种子流形叫作Hk-平面.把H1-平面叫作四元测地线. Hk-平面和∂HnH的交是的一个光滑嵌入，称为Hk-链.把H1-链就叫作链.

类似的，四元超平面和HnH的交是一个全测地四元超曲面，称为在HnH上的四元超平面，它的边界是光滑嵌入∂HnH中的（4n - 1）-维球，称为超链.

若（x，t）∈H，则把x = 0叫作垂直轴，记为V.经过∞的链可以表示成垂直投影

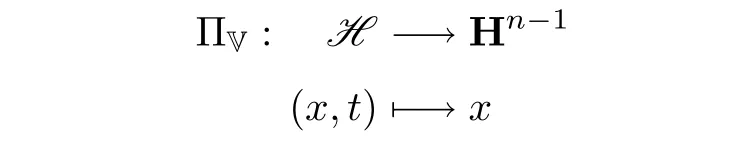
的纤维.把这样的链叫作垂直链.不经过∞的链叫作有限链.

如果C是四元线性子空间，那么存在唯一的一个稳定点集是C的反射，记作ιC.比如，保持垂直轴x = 0的反射就是通常的欧几里德反射（x，t）■→（-x，t），表示成对角矩阵

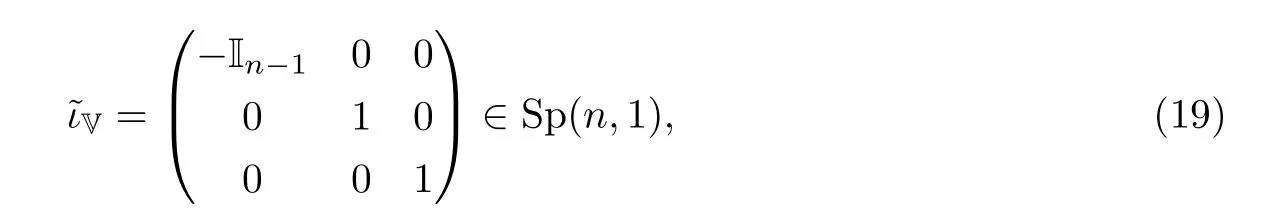
其中In-1是（n - 1）×（n - 1）单位矩阵.

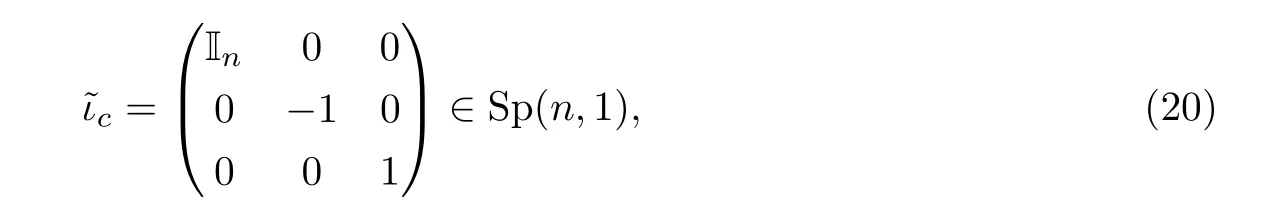
其中反射在HnH的球模型和Siegel模型上分别为

和

令L⊂HnH为一个Hk-平面且它的边界∂L =¯L∩∂HnH是一个Hk-链.那么通过判断∞是否在∂L内，可以分成如下两种情况.如果∞∈∂L，称∂L是垂直的；如果∞/∈∂L，称∂L是有限的. 把L中的反射记为ιL.如果∂L是有限的则ιL（∞）∈H叫做∂L的中心，记为OL.

例3.1取Hk-平面L =｛（0，···，0，ξn-k+1，···，ξn）∈Hn｝，则

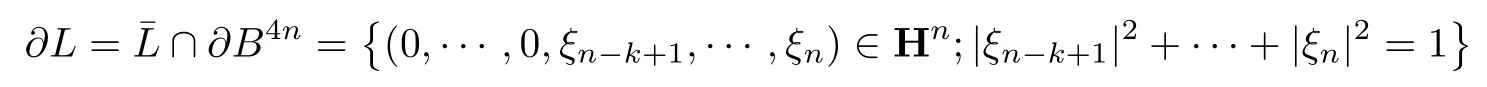
为球B4n上的链，通过Cayley变换可以把它变换为Siegel域上的垂直链

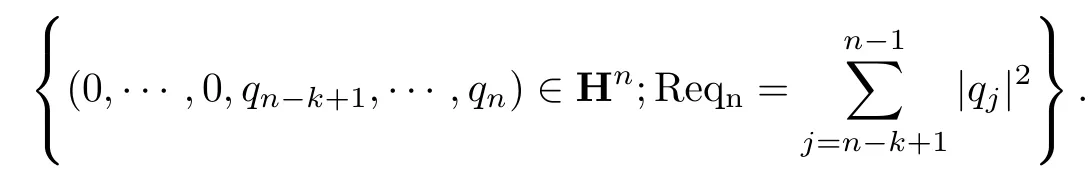
特别的，取k = 1，n = 2时，得到链｛（q1，q2）∈H2；Req2= 0｝，投影到H上为｛（0，q2）｝.

例3.2取Hk-平面L =｛（ξ1，···，ξk，0，···，0）∈Hn｝，则

为球B4n上的链，通过Cayley变换可以把它变换为Siegel域上的有限链

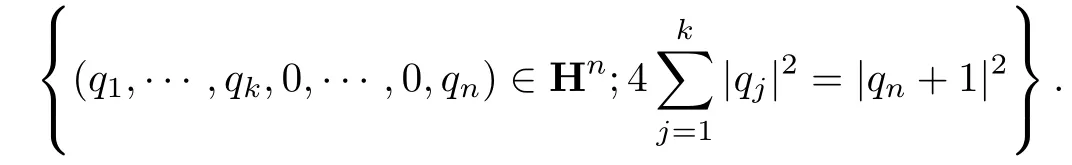
通过§2中的映射（16），可以把如上有限链投影为Heisenberg群上的有限链

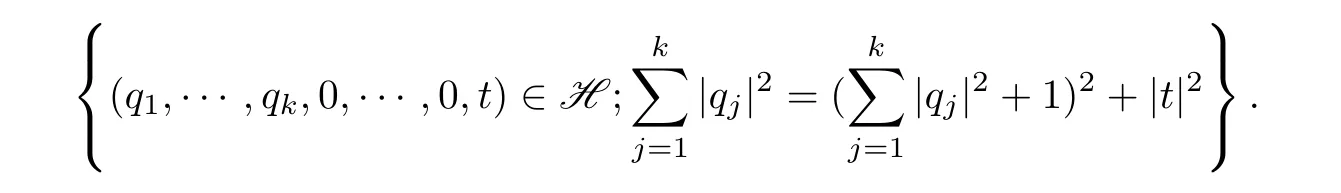
进一步地，垂直投影ΠV: H→Hn-1可以把∂L投影到Hn-1的一个实（4k - 1）-维球

定理3.1令∂L⊂∂HnH= H∪｛∞｝为一个Hk-链且ΠV: H→Hn-1为垂直投影.那么1.如果∂L是垂直的，则ΠV（∂L -｛p∞｝）是Hn-1的一个（k - 1）-维H-仿射子空间且

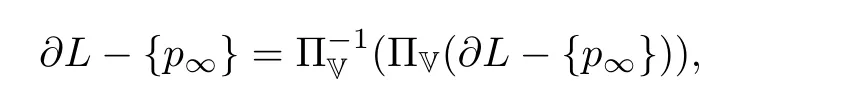
p∞是Siegel域Σ中的无穷远点.

2.如果∂L是有限的，则ΠV是∂L到Hn-1的一个实（4k - 1）-维球的一个双射.

3.两个Hk-链的垂直投影之间相差一个垂直变换.

证1.由于p∞∈∂L，ιL在L中是一个保持p∞的变换，因此也保持与∂HnH相切于p∞处的四元超平面H（p∞）.相应地，在Σ的仿射片上，ιL为仿射变换，它的稳定点集L-｛p∞｝是一个四元仿射空间.由于通过p∞的四元直线有界于垂直链，∂L是一些垂直链的集合，因此ΠV（∂L）是（k - 1）-维四元仿射子空间.

2.假设∂L是中心为OL的有限Hk-链.存在唯一的包含L的垂直Hk+1-链L+.由1，ΠV（∂L+）是Hn-1中的一个k-维仿射子空间.把Hn-1由ΠV（∂L+）代替，可以假设k = n - 1.

令τ为把OL映到V上的变换，则τ（L）是中心在V上的一个Hk-链.因此可以假设OL∈V. V是唯一的包含OL和∞的链，且ιL交换OL和∞.因此ιLV = V，即L和V是正交的.因此2成立.

3.证明与2类似.

当n = 2时，由定理3.1可以直接得到如下推论.

推论3.1链在H上的垂直投影为一个点或者一个圆.

推论3.2如果两个链的垂直投影相同，则他们之间只相差一个垂直变换.

如果c∈H是一个有限链，那么把ΠV（c）∈H的半径定义为链c的半径.

定理3.2 1.令p，q∈H，则存在唯一的链经过p，q.

2.令p∈H且ξ∈TpH - Hp是经过p点的切向量，那么存在唯一的链经过p且与ξ相切.

证1.存在唯一的P（Hn，1）中的投射直线经过p，q∈P（Hn，1）.那么它的边界就是所求的链.

2.由于ξ是一个非零的切向量，存在唯一的经过p与ξ相切的投射直线.因为p∈H且ξ/∈Hp，故这条直线不与∂HnH⊂P（Hn，1）相切，那么它与∂HnH的交是所求的链.

令α⊂H2H为四元测地线｛0｝×H1H有界于垂直轴V∈H .记

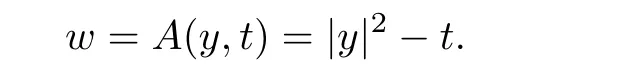
进一步地，把投影Πα: H2H→α限制在H - V的边界上，这把双曲几何嵌入到Heisenberg几何中，即双曲平面对应于H - V中与V垂直的链.这些链覆盖H - V，且通过

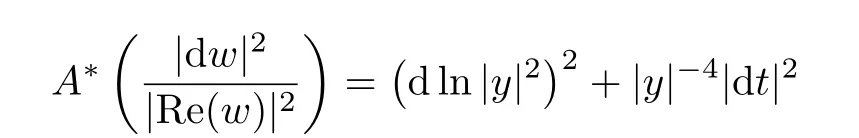
把双曲度量变换到H - V上的度量.

V的稳定子是如下复合的像

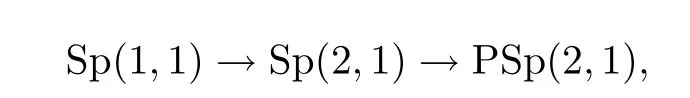
嵌入Sp（1，1）■→Sp（2，1）为

其中D∈Sp（1，1）. Sp（1，1）的中心是固定V的反射.在球模型中，正交投影Πα: H2H→α可以表示为Πα（q1，q2）=（0，q2）.

§4　 R-圆

链提供了很多Heisenberg群上的几何对象.另一方面，与链相类似，也可以考虑全实测地子空间的边界.

把Hk-平面定义中的全测地子流形用全实全测地子流形代替，可以得到Rk-平面的定义，即对于任意的x∈B4n，存在g∈Sp（n，1）把x映射到球心e，令F′⊂TeBn为过球心的一个k-维四元线性子空间，存在唯一的一个过球心且与F′相切的全实全测地子流形.记g（F′）= F.由于g是等距的，通过g-1可得唯一的包含x且与F相切的全实全测地子流形.把这种子流形叫作Rk-平面. 把Rk-平面的边界称作Rk-1-球. R1-球叫作R-圆.把HnH中的Rn-球叫作R-形式. Rk-1-球是光滑的实（k - 1）-维流形.

下面给出HHn上的R-球的一些性质（复双曲空间下相应的结论参见［9］§4，另一种研究复双曲空间下R-球的方法参见［12］§9）.定义实球

回顾子流形S⊂∂HnH是qc-水平的定义，有

定理4.1 P∈HnH是一个Rk-平面，那么R-球∂P⊂∂HnH是qc-水平的子流形.

证令p∈∂P，标准的qc-水平空间可以定义为

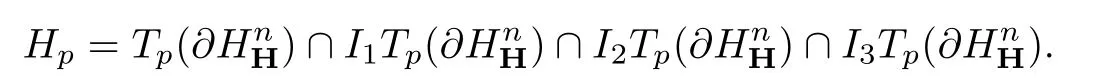
只需要证明

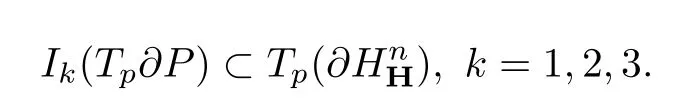
通过适当的坐标变换，可以假设P = BkR×｛0n-k｝=（x1，···，xk，0，···，0），其中xj∈R且p =（1，0，···，0）.那么Tp（∂H）= ImH×Hn-1，IkTp（∂HnH）= ImH×Hn-1，k = 1，2，3且Tp（∂P）=｛0｝×Rk-1×｛0｝，则

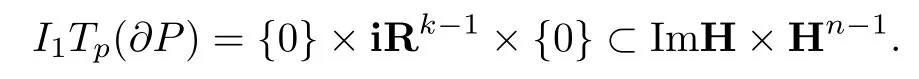
同理可证，I2Tp（∂P）⊂ImH×Hn-1和I3Tp（∂P）⊂ImH×Hn-1.命题成立.

与链类似，Heisenberg几何中的R-球分为有限R-球和无限R-球两种.如果R-球S包含∞则称S是无限R-球，如果不包含∞则称S是有限R-球.

例4.1取Rk-平面L =｛（0，···，0，xn-k+1，···，xn）∈Rn｝，则

为实球B4nR上的R-球，通过Cayley变换可以把它变换为Siegel域上的垂直R-球

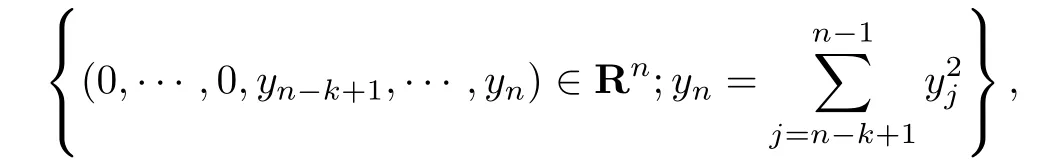
这是一个抛物面.

例4.2取Rk-平面L =｛（x1，···，xk，0，···，0）∈Rn｝，则S =¯L∩∂BnR=（x1，···，xk，0，···，0）∈Rn；x21+···+ x2k= 1

为实球BnR上的R-球，通过Cayley变换可以把它变换为Siegel域上的有限R-球

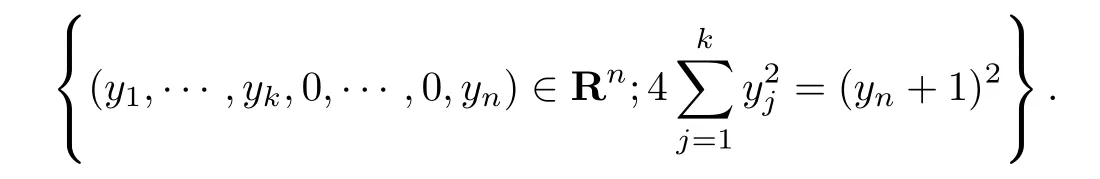
通过§2中的映射（16），可以把如上有限R-球投影为Heisenberg群上的有限R-球

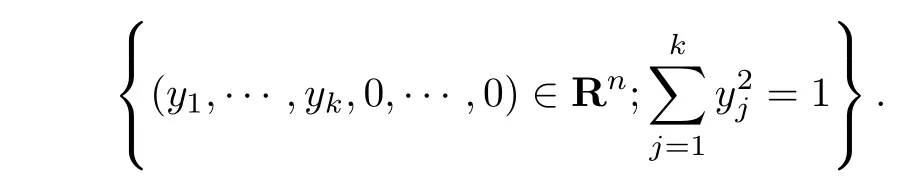
性质4.1令S⊂M为四元切触流形（M4n-1，g，Q）的一个水平子流形，那么有dimS＜n.

证对于任意的s∈S，把dΘ限制到Hs上是一种反对称结构. Xs，Ys是切向量，把他们延拓为S上的光滑向量场，在这种结构下TsS∈Hs是迷向的.那么，因为Xs，Ys和［X，Y］（s）∈TsS均属于Hs= Ker（Θ），则

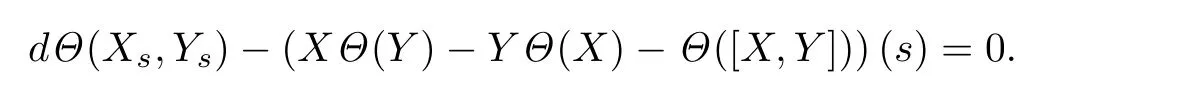
由于TsS是迷向的，所以dimTsS≤14dimHs= n - 1.

例4.3与标准的全实子空间HR2⊂HH2对应的无限R-圆是实轴

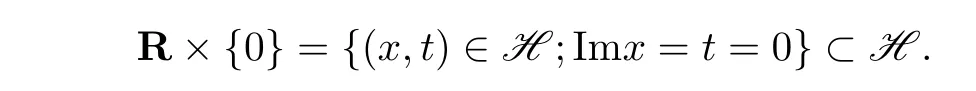
任何一个H中的无限R-圆可以从R×｛0｝通过一个Heisenberg等距变换得到.

为了简便起见，本节的余下部分只考虑n = 2的情况，即只考虑实维数为7的Heisenberg群上的R-圆.有限R-圆R的中心由∞在反射ιR下的像定义（无限R-圆的中心定义为∞）.有QB2R⊂B8，k = 1，2，3，其中Q由 §2中的（1）定义.

考虑一个以原点为中心且包含于QB2R⊂B8的R-圆.把这种R-圆叫作纯虚的R-圆，记为RQ.为了简便起见，只考虑以原点为中心，包含于I1B2R的R-圆，记为RI1.把（x，t）写成柱坐标的形式，为（x = a + bi + cj + dk = reˆnθ，t = t1i + t2j + t3k），其中

（参见［15］p.1646）.

（x，t）∈H在Cayley变换下对应于球上的点

因此RI1在柱坐标下可以由如下方程决定:

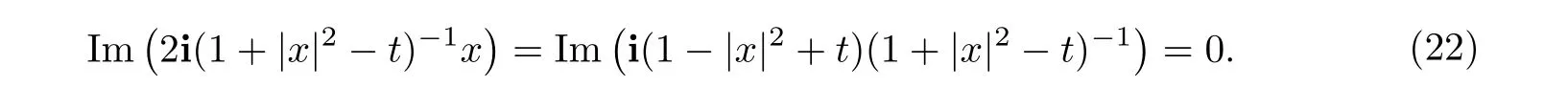
即:

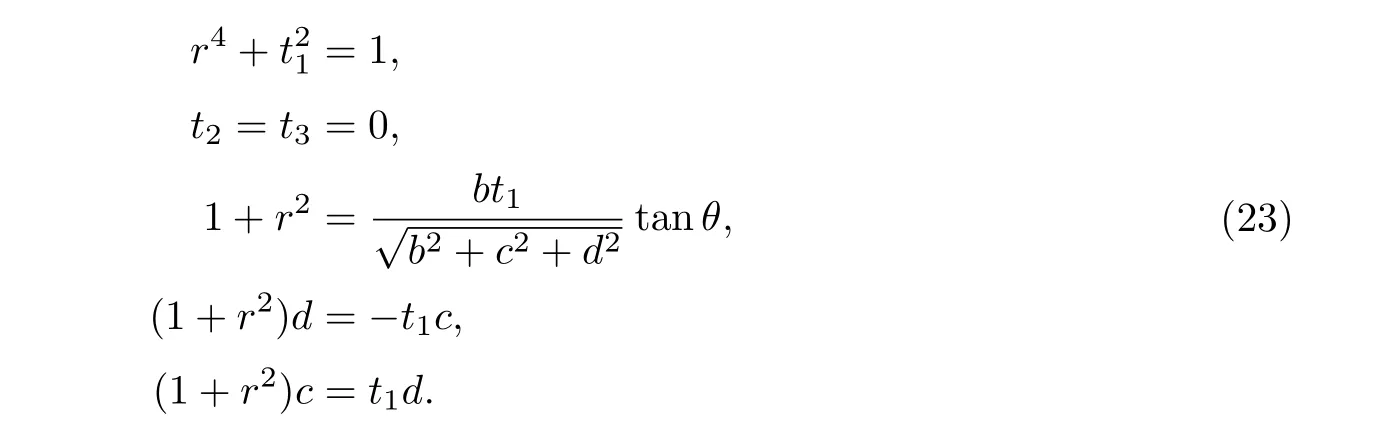
定理4.2任何一个R-圆可以看成是RQ在Heisenberg作用下的像.

证显然可以通过Heisenberg作用把RQ变换成RI1，因此只需要证明任何一个R-圆可以看成是RI1在Heisenberg作用下的像.考虑有限R-圆R⊂H，它的反射是ιR: H→H .可以通过Heisenberg作用把R的中心ιR（∞）变换到原点0∈H，因此不妨假设R的中心是0.反射ιR不改变包含0和∞=ιR（0）的链，即垂直轴V.把ιR限制到V上是一个反对和，它有两个固定点.由于ιR交换0和∞，如果ιR|V的固定点是（0，±r20i），其中r0＞0.通过Heisenberg涨缩可以假设ιR固定（0，±i）∈V.

ιI1表示反射，由于（0，±i）∈RI1且ιI1（V）= V，则ιR◦ιI1保持V不变，且固定（0，0），（0，±i），∞.因此ιR◦ιI1固定V，令

有:

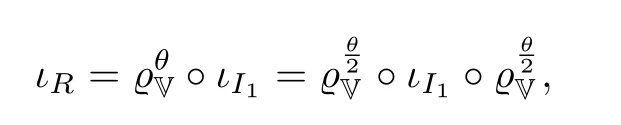
如果R是一个有限R-圆，存在唯一的Heisenberg变换T使得T（R）的中心是原点.那么存在一个Heisenberg变换

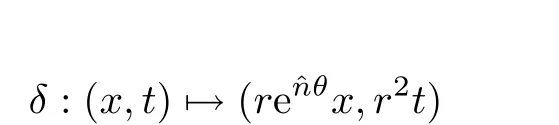
使得T（R）=δ（RI1）.把四元数r2e2ˆnθ定义为R-圆R的半径.显然RI1的半径是1.

［1］Ivanov S，Vassilev D. Conformal quaternionic contact curvature and the local sphere theo

rem［J］. J Math Pures Appl，2010，93: 277-307.

［2］Ivanov S，Vassilev D. Quaternionic contact manifolds with a closed fundamental 4-form［J］. Bull London Math Soc，2010，42: 1021-1030.

［3］Ivanov S，Minchev I，Vassilev D. Quaternionic contact Einstein structures and the quaternionic contact Yamabe problem［A］. Rhode Island: Mem Amer Math Soc，2014，231.

［4］Ivanov S，Vassilev D. The Lichnerrowicz and Obata first eigenvalue theorems and the Obata uniqueness result in the Yamabe problem on CR and quaternionic contact manifolds［J］. Nonlinear Anal，2015，126: 262-323.

［5］Ivanov S，Minchev I，Vassilev D. Solution of the qc Yamabe equation on a 3-Sasakin manifold and the quaternionic Heisenberg group［J］. arXiv:1504.03142v1

［6］Ivanov S，Vassilev D. Extremals for the Sobolev Inequality and the quacternionic contact Yamabe Problem［A］. Imperial College Press Lecture Notes［C］. Hackensack: World Scientific，2011.

［7］Apanasov B，Kim I. Cartan angular invariant and deformations of rank 1 symmetric spaces［J］. Mathematics，2007，198（2）: 147-169.

［8］Wang Wei. The Yamabe problem on quaternionic contact manifolds. Ann Mat Pura Appl，2007，186: 359-380.

［9］Goldman W. Complex hyperbolic geometry［A］. Oxford Mathematical Monographs［C］. New York: Clarendon Press/Oxford University Press，1999.

［10］Biquard O. Asymptotically symmetric Einstein metrics［J］. Ast´erisque，2000，265: 1-109.

［11］Shi Yun，Wang Wei. On conformal qc geometry，spherical qc manifolds and convex cocompact subgroups of Sp（n + 1，1）［J］. DOI 10.1007/s10455-015-9492-y

［12］Jcobowitz H. An introduction to CR structures［A］. Mathematical Surveys and Monographs 32［C］. New York: American Mathematical Society，1990.

［13］Yue Chengbo. Mostow rigidity of rank 1 discrete groups with ergodic Bowen-Margulis measure［J］. Invent Math，1996，125: 75-102.

［14］Corlette K. Hausdorff dimension of limit sets I［J］. Invent Math，1990，102: 521-541.

［15］Chang Derchen，Markina I，Wang Wei. On the Cauchy-Szeg¨o kernel for quaternion siegel Upper half-space［J］. Complex Anal Oper Theory，2013，7: 1623-1654.

Chain and R-circle on quaternionic Heisenberg group and their properties

SHI Yun
（Department of Mathematics，Zhejiang University，Hangzhou 310027，China）

This paper defines chain and R-circle on quaternionic hyperbolic space，and gives the property of chains under the vertical projection. The uniqueness of chain passing through two distinct points and qc-horizontality of R-circles are proved，and the relationship between R-circle and pure imaginary R-circle is given.

quaternionic hyperbolic space；quaternionic Heisenberg group；chain；R-circle MR Subject Classification: 53C15；53C56

O184

A

1000-4424（2016）01-0090-11

2015-11-13

2016-01-15

国家自然基金（11171298；11571305）