关于图的最小Q-特征值

吴宝丰，庞琳琳，沈富强

（上海理工大学理学院，上海200093）



关于图的最小Q-特征值

吴宝丰，庞琳琳，沈富强

（上海理工大学理学院，上海200093）

研究了基于n阶二部图和s阶完全图构造的一个图类，得到了该图类的无符号拉普拉斯最小特征值（即最小Q-特征值）的一个可达上界为s.基于此，对于任意给定的正整数s和正偶数n，构造了最小Q-特征值为s的一类n + s阶图.另外，对于任意给定的

无符号拉普拉斯矩阵；最小Q-特征值；界；最小度

§1　引　言

本文考虑简单无向图.设图G =（V，E），其中V = V（G）=｛1，2，···，n｝是G的顶点集，E = E（G）=｛ij?i，j∈V，且i～j｝是G的边集，n称为G的阶数. A（G）=（aij）表示G的邻接矩阵，其中当ij∈E（G）时，aij= 1；否则aij= 0. Q（G）= D（G）+A（G）表示G的无符号拉普拉斯矩阵，简称为G的Q-阵，其中D（G）= diag（d1，d2，···，dn）为G的度对角矩阵，di代表顶点i的度，δ（G）代表最小度，N（i）= NG（i）表示顶点i在G中的邻点集.

近年来图的Q-阵受到了国内外众多学者的关注，这主要归功于文献［1-2］，因为它们显示，对于图的Q-阵，同谱不同构的图的数目要比邻接矩阵和拉普拉斯矩阵少，这说明研究Q-阵可能更有意义.国际著名图论专家Cvetkovi´c和Simi´c提出要建立Q-谱理论，并综述了相关结论（见［3-5］），进一步推动了对Q-阵的研究.由于Q-阵的二次型为

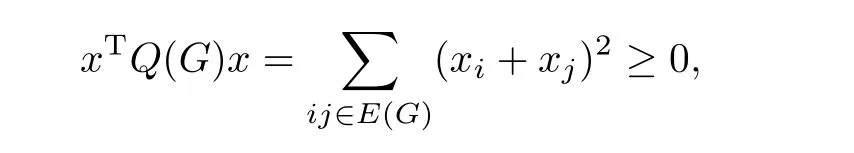
所以Q（G）是半正定实对称矩阵，它的特征值都是非负实数，记为qi（G）（i = 1，2，···，n），称为图G的Q-特征值，SpecQ（G）=｛q1（G），q2（G），···，qn（G）｝是一个多重集合，称为图G的Q-谱.不妨设特征值已从大到小排列为q1（G）≥q2（G）≥···≥qn（G）≥0，其中qmin（G）= qn（G）称为G的最小Q-特征值，若x是Q（G）的相应于特征值q的特征向量，则对于任意i = 1，2，···，n，有（q - di）xi=对于最小Q-特征值，若G是连通图，则qmin（G）= 0当且仅当G是二部图（见［6］），所以Desai和Rao（见［7］）等人提出以qmin（G）来衡量图的非二部性，这说明研究图的最小特征值qmin（G）是非常有意义的，相关文献如［8-10］.

设a为实数，记「a⌉为不小于a的最小整数，即取a的上整.设G1，G2是两个顶点不交的图，G1VG2表示在G1∪G2的基础上，连接G1和G2之间所有点对所得到的图.设u，v分别是G1，G2中的点，G1u·vG2表示在G1∪G2的基础上，合并u，v两点所得到的图.在不致混淆的情况下，G1u·vG2可以简记为G1·G2.

§2研究了基于n阶二部图H和完全图Ks构造的一个图类，得到了该图类的最小Q-特征值的一个可达上界为s.基于此，对于任意给定的正整数s和正偶数n，构造了最小Q-特征值为s的一类n+s阶图（定理1.1）.§3，对于任意给定的最小度δ和阶数n，在满足条件下，构造了最小Q-特征值为δ- 1的一类n阶图（定理1.2）.

§2最小Q-特征值为任意给定的正整数的一类图

给定n阶图H，定义图类

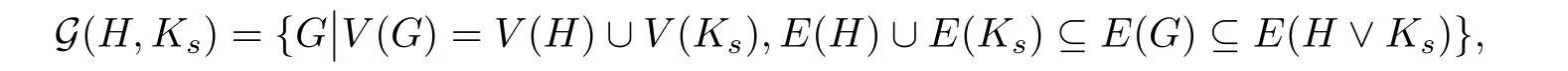
［11］研究了H为二部图时图类G（H，K1）的最小Q-特征值.本节研究H为二部图时图类G（H，Ks）（s≥1）的最小Q-特征值.

引理2.1 （见［12］）设λmin是n阶实对称矩阵A的最小特征值，则对于任意n维非零向量x，有，等式成立当且仅当x是A的相应于λmin的特征向量.

引理2.2 （删边插值）（见［13］）设q1，q2，···，qn是图G的Q-特征值，s1，s2，···，sn是G-e的Q-特征值，其中e是G的一条边，则q1≥s1≥q2≥s2≥···≥qn≥sn≥0.

引理2.3 设n阶二部图H是图G的一个点诱导子图，H与G - H之间有t条边，则qmin（G）≤进一步，若等式成立，则对于任意i∈V（G - H），i在H两部中的邻点数相同.

证设H两部的顶点集分别为V1，V2，其中|V1| = n1，|V2| = n2，n1+ n2= n.对于图G，取x =（1，···，1，-1，···，-1，0，···，0）T，其中V1中的点对应分量1，V2中的点对应分量-1，其余点对应分量0，由引理2.1知，

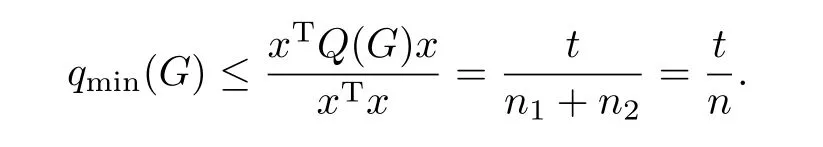
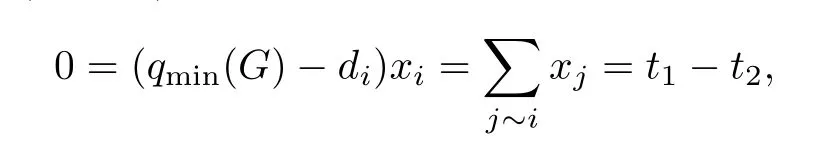
从而t1= t2.

综上所述，结论得证.

定理2.1设二部图H两部的顶点数分别为n1，n2，G∈G（H，Ks），则qmin（G）≤s.进一步，若等式成立，则（a）G = H V Ks；（b）n1= n2.

证设H与G - H之间有t条边，则由引理2.3知，

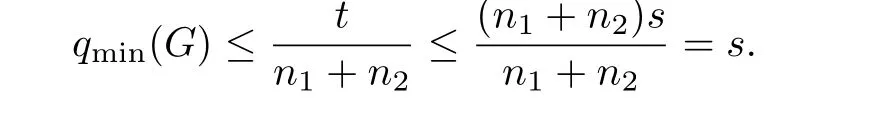
进一步，若qmin（G）= s，则上式所有不等式取到等号.第二个不等式取到等号时，显然有G = H VKs.此时，考虑第一个不等式取到等号，根据引理2.3知，对于任意i∈V（Ks），i在H两部中的邻点数相同，从而n1= n2，证毕.

考虑H为正则二部图，则G = H V Ks满足定理2.1中等式成立的2个必要条件，在此基础上，对于任意给定的正整数s和正偶数n，下面构造最小Q-特征值为s的一类n + s阶图，记QG（x）= det（xI - Q（G））为G的无符号拉谱拉斯特征多项式，即G的Q-特征多项式.

引理2.4（见［14］）设G1为n1阶r1-正则图，G2为n2阶r2-正则图，则

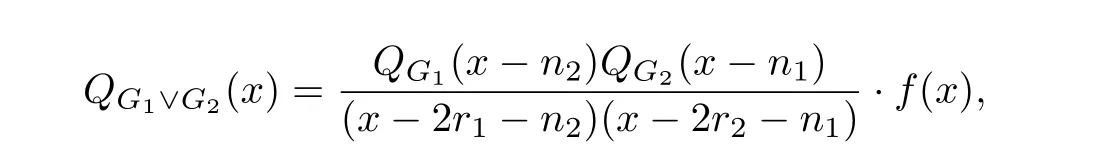
其中f（x）= x2-［2（r1+ r2）+（n1+ n2）］x + 2（2r1r2+ r1n1+ r2n2）.

推论2.1设H为n阶r-正则图，则

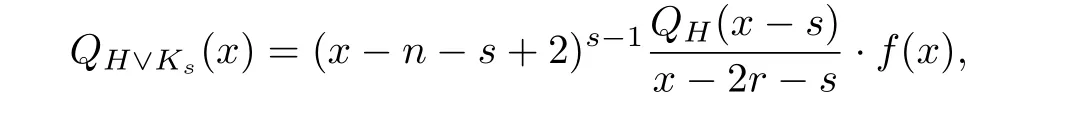
定理2.2设H为n阶r-正则二部图，r≥1，n≥2r，则

（a）对于任意整数s∈｛1，2，···，2r｝，有qmin（H V Ks）= s；

证由推论2.1知，

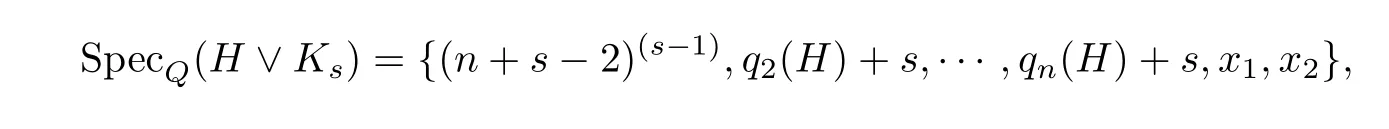
其中qn（H）= 0，x1，x2为

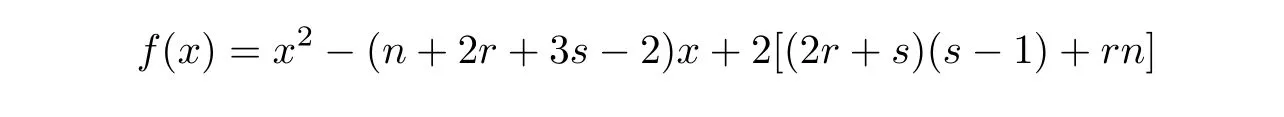
的两个根.设q为f（x）= 0的较小根，即

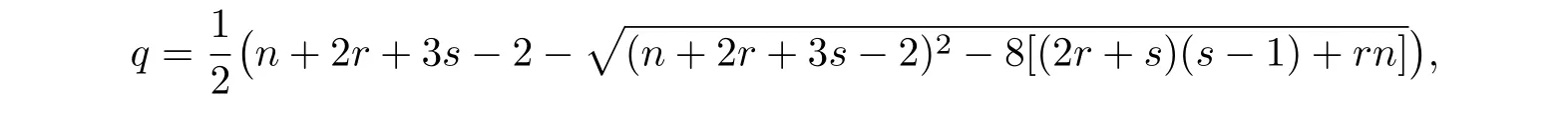
由于n≥2r≥2，所以

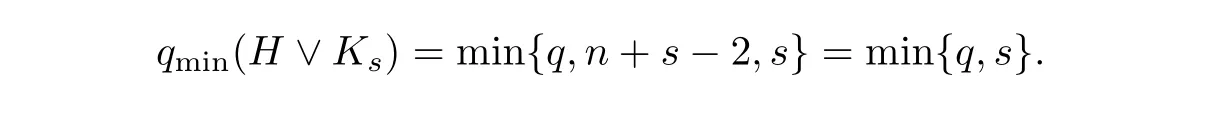
从而，qmin（H V Ks）= s等价于q≥s.经计算知，q≥s又等价于

当s = 2时，（1）式等价于（2r - 2）n≥0，显然也成立，所以qmin（H V K2）= 2；

当s∈｛3，···，2r｝时，（1）式的左边大于等于0，而右边小于0，从而（1）式成立，所以qmin（H V Ks）= s.

综上所述，定理得证.

推论2.2设H为n阶r-正则二部图，r≥1，n≥2r，则有qmin（HVK1）= 1，qmin（HVK2）= 2.

推论2.3设H为简单图，若qmin（H VK1）＜1或者qmin（H VK2）＜2，则H不存在完美匹配.

证假设H存在完美匹配，则H的顶点数为偶数，不妨设为2t，则H包含1-正则生成子图tK2，由引理2.2（删边插值）及推论2.2知，qmin（HVK1）≥qmin（tK2VK1）= 1，且qmin（HVK2）≥qmin（tK2V K2）= 2，矛盾，证毕.

引理2.5（见［11］）设G∗是图G增加一条边e = ij后所得到的图，x是G的相应于qmin（G）的一个特征向量，若xi+xj= 0，则qmin（G∗）= qmin（G），且x也是G∗的相应于qmin（G∗）的一个特征向量.

定理1.1的证明对于任意给定的正整数s 和正偶数n， 显然0，从而，即亦即令H为任意n阶r-正则二部图.若s≤2r，则由定理2.2（a）知，，则由r得，再根据定理2.2（b），得qmin（H V Ks）= s.

取x =（1，···，1，-1，···，-1，0，···，0）T，其中H的两部分别对应分量1，-1，Ks对应分量0.

则

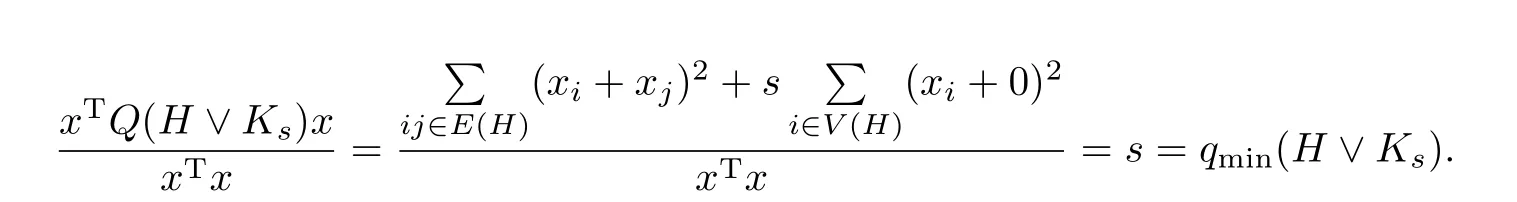
由引理2.1知，x =（1，···，1，-1，···，-1，0，···，0）T是相应于qmin（H V Ks）的一个特征向量. 而H的二部之间任意点对（i，j），即i，j分属于H的两部，满足xi+ xj= 0，根据引理2.5，在H的二部之间添加若干条边后，H V Ks的最小Q-特征值保持不变，定理得证.

例2.1构造最小Q-特征值分别为1和2的图类.这里s = 1，2，对于任意正偶数n = 2t，有= 1，n阶1-正则二部图即为tK2，记

例2.2构造最小Q-特征值分别为3和4的图类.这里s = 3，4，当n = 2时，有

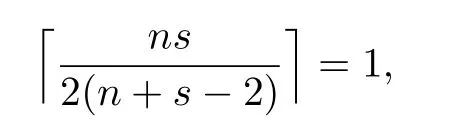
2阶1-正则二部图即为K2；当正偶数n≥4时，有

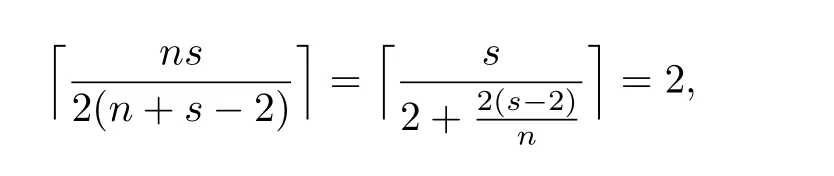
2-正则二部图即为若干个偶圈的并，记

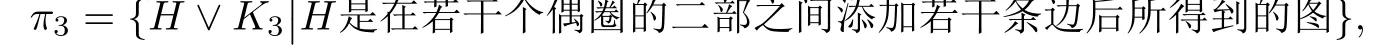
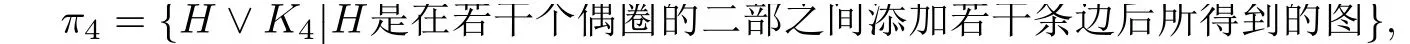
则任意G∈｛K2V K3｝∪π3，有qmin（G）= 3；任意G∈｛K2V K4｝∪π4，有qmin（G）= 4.

§3　最小Q-特征值为δ- 1的一类图

众所周知，当图G（阶数＞1）连通时，qmin（G）＜δ（G）（见［15］），下面构造最小Q-特征值为δ（G）- 1的一类n阶图.

引理3.1设n阶图G的最小度为δ，度为δ的顶点至少有2个，且它们相邻，则qmin（G）≤δ-1.

引理3.2设G =（V，E），Vk⊆V，|Vk| = k，G［Vk］是一个团，且Vk中任一点在V Vk中有相同的邻点集，设Vk中点的度为d，则d - 1至少是Q（G）的k - 1重特征值.

证设Vk=｛1，2，···，k｝，x =（x1，···，xk，xk+1，···，xn）T，其中xi对应顶点i（i = 1，···，n），且x1+···+ xk= 0，xk+1=···= xn= 0，则对于任意i∈Vk，有

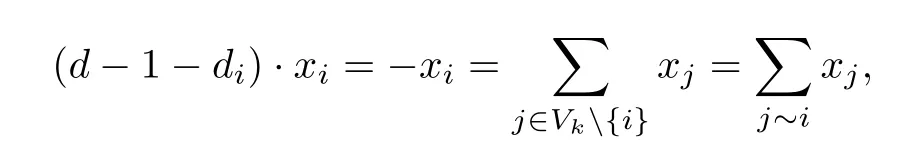
对于任意i∈V Vk，或者Vk⊂N（i），或者Vk∩N（i）=∅，从而

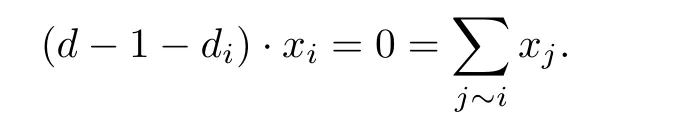
故x是Q（G）的相应于d-1的特征向量，且d-1的特征子空间的维数至少为k -1，所以d-1至少是Q（G）的k - 1重特征值.

引理3.3设G = Kn1·Kn2，n1≥2，n2≥2，则

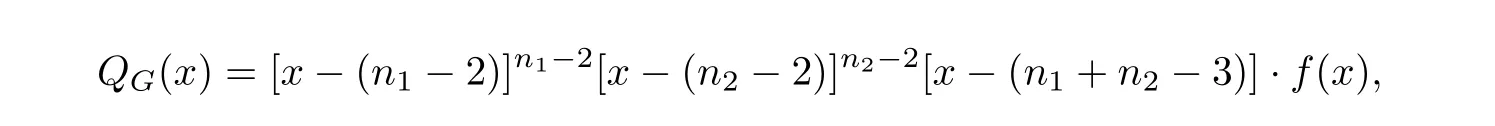
其中f（x）= x2-（2n1+ 2n2- 5）x + 4n1n2- 6n1- 6n2+ 8.

证设Kn1和Kn2的公共点为u，V1= V（Kn1）｛u｝，V2= V（Kn2）｛u｝，则V1，V2都是团，由引理3.2知，G = Kn1·Kn2的Q-谱中包含n1-2个特征值n1-2以及n2-2个特征值n2-2.剩下的3个特征值可按如下方法求得.设x是Q（G）的特征向量，点u对应分量x0，V1中的点都对应分量x1，V2中的点都对应分量x2，则有

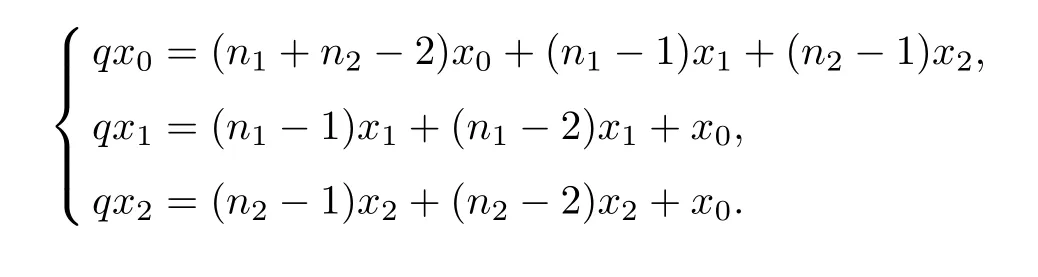
即

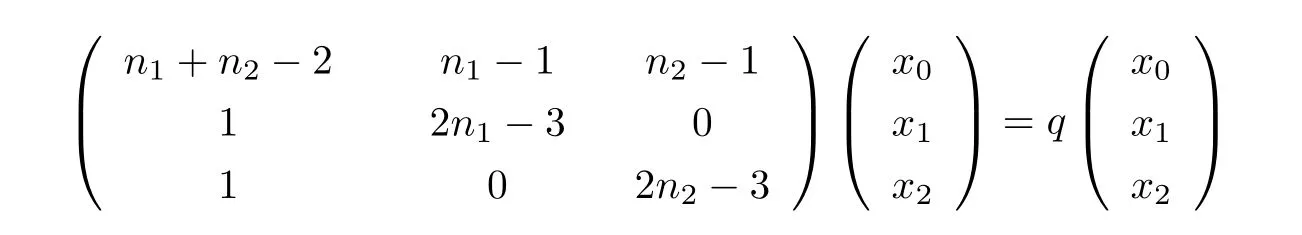
相应的特征多项式为

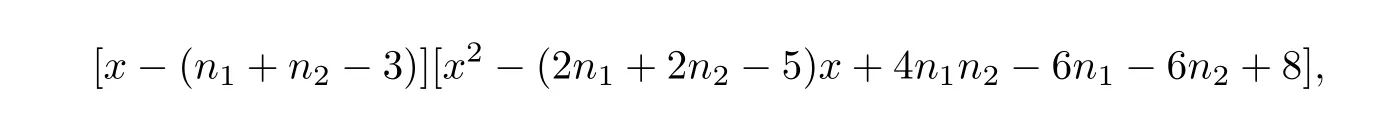
它的3个实数根也是Q（G）的特征值，且与n1-2个特征值n1-2以及n2-2个特征值n2-2并不重复，因为引理3.2的证明表明那些特征值的特征向量在V1中对应的分量是不能全相等的，结论得证.

推论3.1设G = Kn1·Kn2，2≤n1≤n2，则Q（G）的最小特征值为n1- 2.

证根据引理3.3，

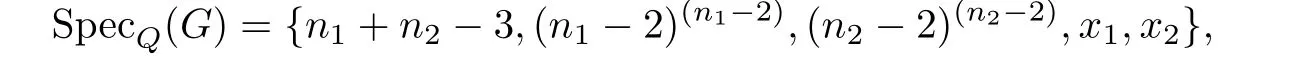
其中x1，x2是f（x）= x2-（2n1+ 2n2- 5）x + 4n1n2- 6n1- 6n2+ 8的两个根.

显然n1+ n2- 3＞n2- 2≥n1- 2，所以Q（G）的最小特征值是f（x）的最小根和n1- 2两者之一.因为f（x）的对称轴为

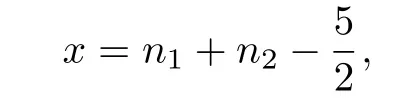
且

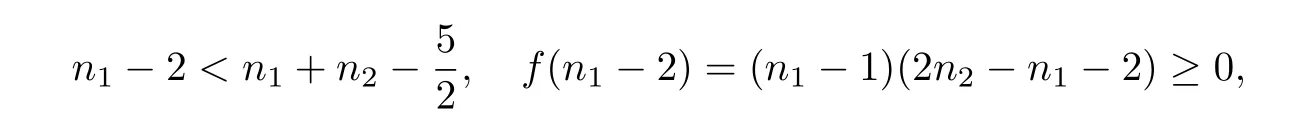
所以n1- 2小于等于f（x）的最小根，从而Q（G）的最小特征值为n1- 2，证毕.

定理1.2的证明任意G∈σδ，n，显然δ（G）=δ，下证qmin（G）=δ- 1.

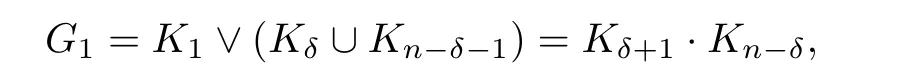
综上所述，qmin（G）=δ- 1.

［1］Van Dam E R，Haemers W H. Which graphs are determined by their spectrum？［J］. Linear Algebra Appl，2003，373: 241-272.

［2］Haemers W，Spence E. Enumeration of cospectral graphs［J］. Eur J Combin，2004，25: 199-211.

［3］Cvetkovi´c D，Simi´c S K. Towards a spectral theory of graphs based on signless Laplacian，I［J］. Publ Inst Math，2009，85（99）: 19-33.

［4］Cvetkovi´c D，Simi´c S K. Towards a spectral theory of graphs based on signless Laplacian，II［J］. Linear Algebra Appl，2010，432（9）: 2257-2272.

［5］Cvetkovi´c D，Simi´c S K. Towards a spectral theory of graphs based on signless Laplacian，III［J］. Appl Anal Discrete Math，2010，4（1）: 156-166.

［6］Cvetkovi´c D，Rowlinson P，Simi´c S K. Signless Laplacians of finite graphs［J］. Linear Algebra Appl，2007，423: 155-171.

［7］Desai M，Rao V. A characterization of the smallest eigenvalue of a graph［J］. J Graph Theory，1994，18: 181-194.

［8］Cardoso D M，Cvetkovi´c D，Rowlinson P，et al. A sharp lower bound for the least eigenvalue of the signless Laplacian of a non-bipartite graph［J］. Linear Algebra Appl，2008，429（11-12）: 2770-2780.

［9］Lima L S，Silvaoliveira C，Abreu N M M，et al. The Smallest eigenvalue of the Signless Laplacian［J］. Linear Algebra Appl，2011，435（10）: 2570-2584

［10］Fan Yizheng，Wang Yi，Guo Huan. The least eigenvalues of the signless Laplacian of nonbipartite graphs with pendant vertices［J］. Discrete Math，2013，313（7）: 903-909.

［11］沈富强，吴宝丰.最小Q-特征值为给定整数的一类图［J］.上海理工大学学报，2014，36（5）: 425-428.

［12］Horn R A，Johnson C R. Matrix Analysis［M］. Cambridge: Cambridge University Press，1985.

［13］Cvetkovi´c D，Rowlinson P，Simi´c S K. Eigenvalue bounds for the signless Laplacian［J］. Publ Inst Math，2007，81（95）: 11-27.

［14］De Freitas M A A，De Abreu N M M，Del-Vecchio R R，et al. Infinite families of Q-integral graphs［J］. Linear Algebra Appl，2010，432（9）: 2352-2360.

［15］Das K C. On conjectures involving second largest signless Laplacian eigenvalue of graphs［J］. Linear Algebra Appl，2010，432: 3018-3029.

MR Subject Classification: 05C50

On the least signless Laplacian eigenvalue of graphs

WU Bao-feng，PANG Lin-lin，SHEN Fu-qiang
（College of Science，University of Shanghai for Science and Technology，Shanghai 200093，China）

A class of graphs constructed by H and Kswas studied，where H is a bipartite graph of order n and Ksis the complete graph of order s. It was shown that a sharp upper bound of the least signless Laplacian eigenvalue（the least Q-eigenvalue）is s. Based on this，for any given positive integer s and positive even number n，a class of graphs of order n + s was constructed which have eigenvalue s as their least Q-eigenvalue. Also，for any given smallest degree δ and order n such that 2≤δ≤， a class of graphs of order n was constructed which have eigenvalue δ- 1 as their least Q-eigenvalue.

signless Laplacian matrix；least Q-eigenvalue；bound；smallest degree

O157.5

A

1000-4424（2016）01-0083-07

2015-05-24

2015-12-11

国家自然科学基金（11301340；11201303）；上海自然科学基金（12ZR1420300）；沪江基金（B14005）