一类非光滑多目标规划问题的最优性条件
周轩伟
(浙江树人大学基础部,浙江杭州310015)
一类非光滑多目标规划问题的最优性条件
周轩伟
(浙江树人大学基础部,浙江杭州310015)
研究了一类非光滑多目标规划问题.这类多目标规划问题的目标函数为锥凸函数与可微函数之和,其约束条件是Euclidean空间中的锥约束.在满足广义Abadie约束规格下,利用广义Farkas引理和多目标函数标量化,给出了这一类多目标规划问题的锥弱有效解最优性必要条件.
非光滑多目标规划;广义Abadie约束规格;广义Farkas引理;最优性必要条件
O221.6
§1 引 言
考虑下列的非光滑多目标规划问题:
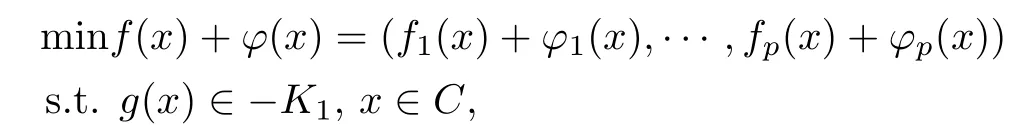
(MPP)其中f =(f1,···,fp): Rn→Rp,g =(g1,···,gm): Rn→Rm. f和g是Rn上的可微多目标函数,ϕ=(ϕ1,···,ϕp): Rn→Rp是Rn上有限值K-凸函数;K,K1分别是Rp,Rm中的尖闭凸锥且intK /=∅,intK1/=∅,C是Rn中的凸子集.
对问题(MPP),当ϕi(x)= s(x|Di)(i = 1,···,p),其中s(x|Di)是Rn中的紧子集Di(i = 1,···,p)的支撑函数,C是Rn的开子集时,文[1-2]给出了问题(MPP)的最优性条件和对偶定理. 当ϕi(x)=(xTBx)1/2,其中B是n×n对称半正定矩阵,f是Rn上的可微函数,C = Rn,p = 1时,文[3]首先提出了问题(MPP),并在满足一种较复杂的约束规格条件下,得到了该问题的最优性必要条件.然后,文[4]证明了Slater约束规格蕴含前文中的约束规格.后来,文[5]将文[3]的问题推广到分式规划.文[6-7]再将该问题推广到极小极大分式规划.在文[3]的约束规格下,文[6-7]给出了相应的最优性必要条件.在这些必要条件的基础上,上述论文也讨论了最优性充分条件或Wolfe型对偶.在问题(MPP)中,当K = Rp+,K = Rm+和C = Rn时,文[8]在问题(MPP)满足Kuhn-Tucker约束规格或Arrow-Hurwicz-Uzawa约束规格([9])时,得到了弱有效解的Kuhn-Tucker型必要条件.当C⊂Rn为一般凸集,p = 1时,文[10]引进了广义的Kuhn-Tucker约束规格和广义的Arrow-Hurwicz-Uzawa约束规格,得到了最优解的Kuhn-Tucker型必要条件.当C⊂Rn为一般凸集,p>1时,文[11]在文[10]的约束规格下,得到了Pareto弱有效解的Kuhn-Tucker型必要条件.
本文研究了非光滑多目标规划问题(MPP).其目标函数为锥凸函数与可微函数之和,约束条件是锥约束.在满足广义Abadie约束规格下,利用广义Farkas引理和多目标函数标量化,给出了这一类多目标规划问题的锥弱有效解最优性必要条件.本文将文[10]和[11]的结果从Pareto弱有效解推广到锥弱有效解,并且将有限个不等式约束推广到锥约束.由于锥约束相当于无限个不等式约束,因此本文的结果是文[10]和[11]的结果在多目标规划中的本质推广.本文中的定理3.1和定理3.2是文[11]中定理3.1和定理3.2的推广.
§2 预备知识
给出本文涉及的基本概念,定义和引理.
定义2.1设S是Rn中的非空子集,点x0∈clS.设点列{xk}⊂S,xk→x0(k→+∞),正数
数列{tk},tk→+∞(k→+∞).若极限d =)存在,则称d是点x0处关于S的切向量.集合T(S,x0)=称为是S在x0处的切锥.
定义2.2设K⊂Rn.若
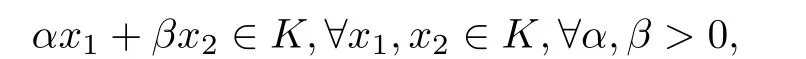
设C是Rn的子集,affC表示C的仿射包,riC表示C的相对内部,
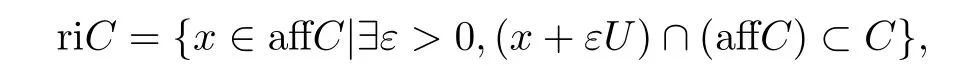
其中U是Rn中的单位球.
定义2.3设X ={x∈Rn|g(x)∈-K1},g在x∗∈X∩C满足广义Abadie约束条件,若
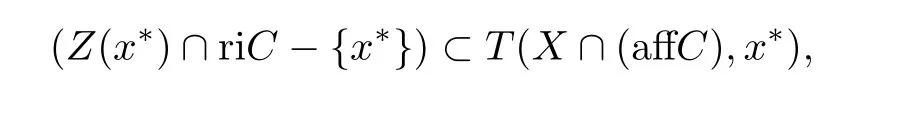
其中
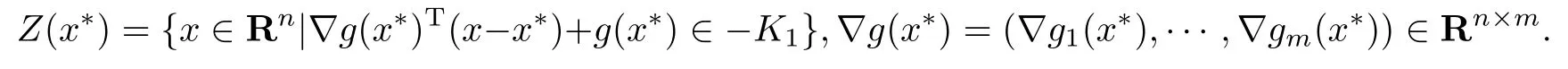
定义2.4设K⊂Rn是具有非空内部的尖凸锥,x0∈Rn.若x∄D,使得
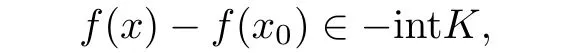
则称x0为多目标规划(MPP)的K-弱有效解,其中D ={x∈C|g(x)∈-K1}.
定义2.5设K⊂Rn是具有非空内部的闭凸锥,若∀x1,x2∈Rn,以及λ∈[0,1]均有

则称f(x)为K-凸函数.

其中domh ={x|h(x)<+∞}.集合
引理2.1[3]设C是Rn的凸子集,假若riC /=∅,(affC)(riC)/=∅,则对于任意的x∗∈
(clC)(riC),有
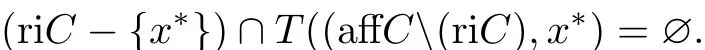
§3 主要结论
在满足广义Abadie约束条件下,给出多目标规划问题(MPP)的锥弱有效解最优性必要条件. 记
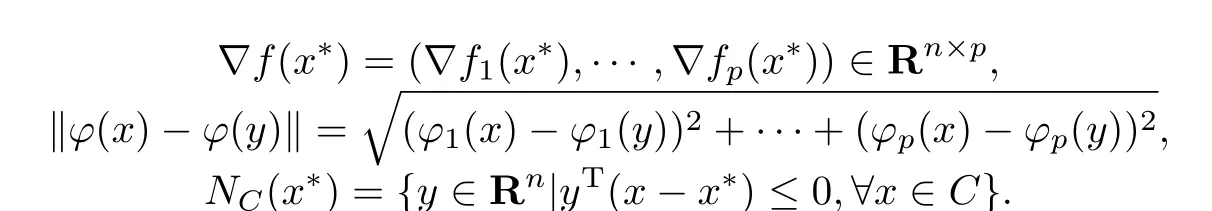
引理3.1若x∗是(MPP)的K-弱有效解,g在x∗处满足广义Abadie约束条件,ϕ是Rn上有限值K-凸函数,并且对任意的x,y∈Rn有‖ϕ(x)-ϕ(y)‖≤L‖x - y‖(L>0).如果Z(x∗)∩riC /=∅,则广义不等式组
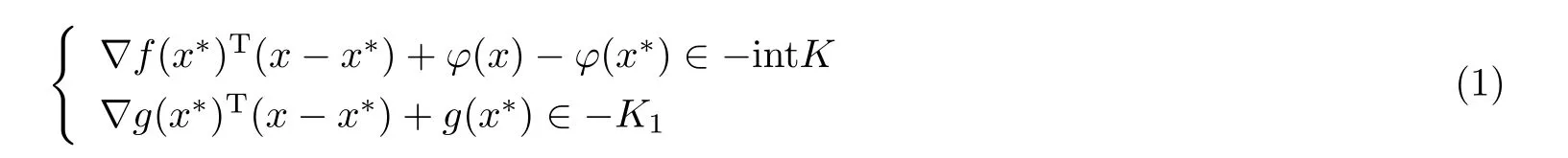
在riC内无解.
证假设存在¯x∈riC满足(1),则¯x∈Z(x∗)即¯x∈Z(x∗)∩riC.因为g在x∗处满足广义Abadie约束条件,由其定义有

所以存在xk⊂X∩(affC)和{tk}⊂R+,tk→+∞(k→+∞)使得

下面分两种情况证明:存在k1,当k≥k1时,xk∈riC.
当x∗∈riC时.由ri(riC)= riC,aff(riC)= affC,知
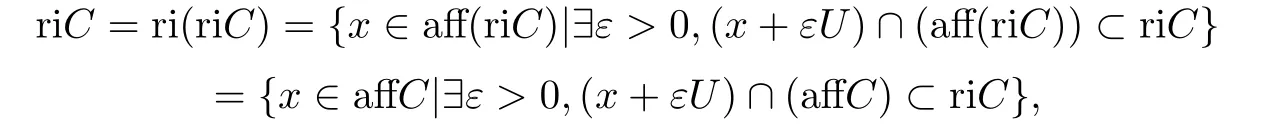
所以存在¯ε>0使得(x∗+¯εU)∩(affC)⊂riC.因为xk→x∗,于是知存在k1,当k≥k1时有xk∈x∗+¯εU,从而xk∈riC.
当x∗∈C iC⊂clC iC时,假设结论不成立,即不存在k1,当k≥k1时,xk∈riC,则存在序列{ki},ki→+∞(i→+∞)使得xki∈affC iC,则由(2)式,有tki(xki-x∗)→¯x - x∗(i→+∞),从而¯x - x∗∈T((affC)(riC),x∗).由引理2.1,对于x∗∈clC iC有
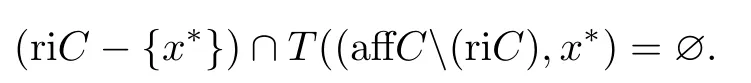
又因为¯x - x∗∈T((affC)(riC),x∗),所以¯x - x∗/∈(riC -{x∗}),即¯x /∈riC,矛盾.所以由上述证明可知,存在k1,当k≥k1时,xk∈riC.
由于¯x满足(1)式,可知¯x /= x∗.由(2)式知,存在k2使得k≥k2,tk≥1.
由于ϕ(x)是Rn上的K-凸函数,所以∀u∈[0,1]有
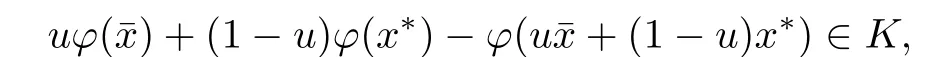
从而有
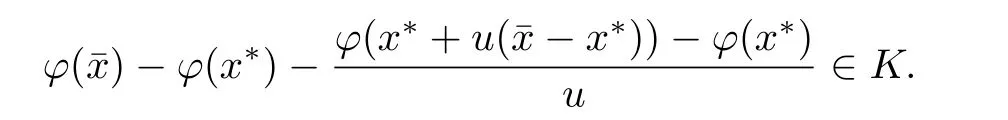
因为tk≥1(k≥k2)有有
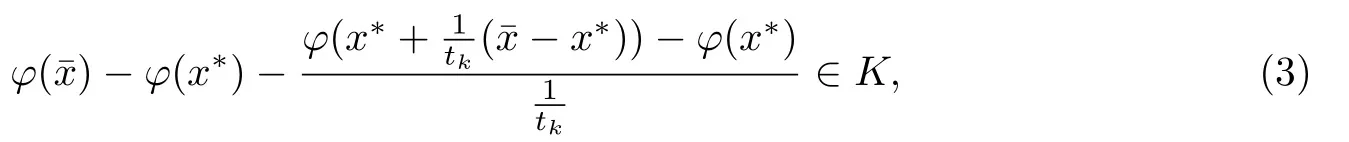
因为对任意的x,y∈Rn有
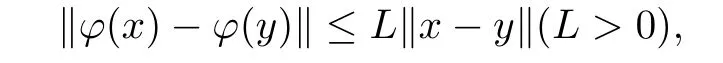
所以
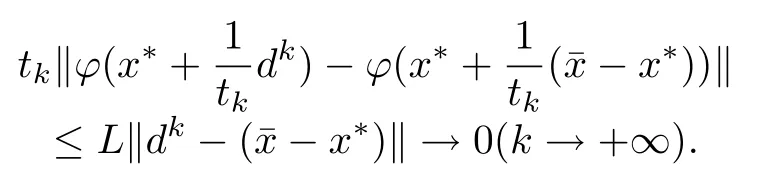
又由

得
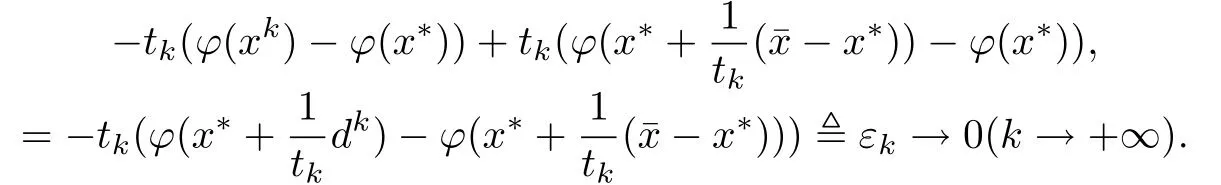
由上式和(3)式知,当k≥k2时有
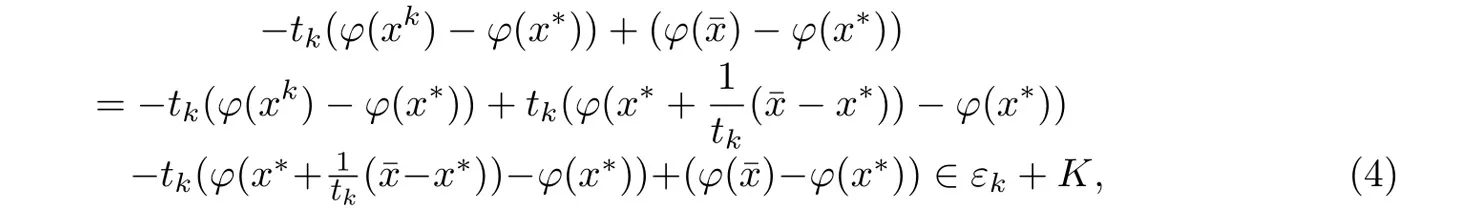
又¯x满足广义不等式组(1)有▽f(x∗)T(¯x - x∗)+ϕ(¯x)-ϕ(x∗)∈-intK.于是存在k3使得当k≥k3时,有
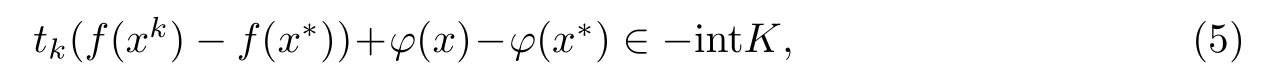
由(4)式,(5)式得
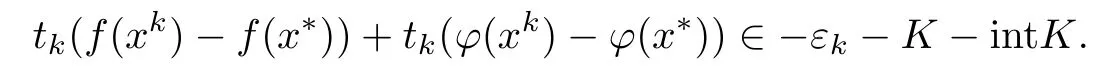
因为εk→0(k→+∞),故存在k4,当k≥k4时有,

取¯k = max{k1,k2,k3,k4},则当k≥¯k时,有
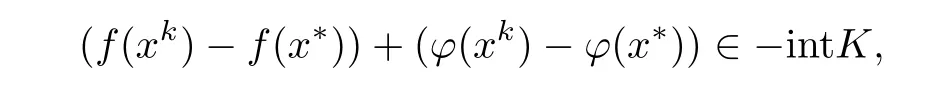
即
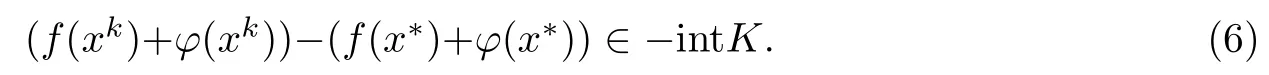
因为xk∈X∩C(k≥¯k),所以(6)式与x∗是(MMP)的K-弱有效解矛盾,从而广义不等式组(1)在riC内无解.
引理3.2设D⊂Rn为凸集,K⊂Rp为凸锥,且intK /=∅,f(x)∈Rp为K-凸函数.若广义不等式组

无解,则存在λ∈K∗{0},使得∀x∈D,有

先证明Y为凸集.设

则存在x1∈D,x2∈D,有
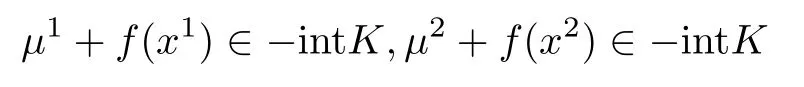
由于K为凸集,故intK为凸集,因此
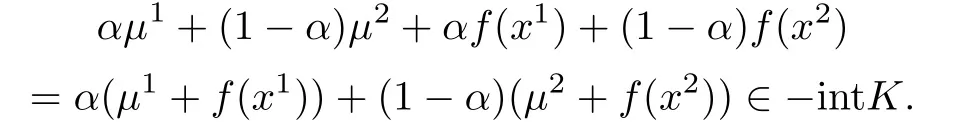
现在

因为f(x)为K-凸函数,以及intK为凸锥,故

由µ1+ f(x1)∈-intK,µ2+ f(x2)∈-intK,不妨设α>0,1 -α>0,故
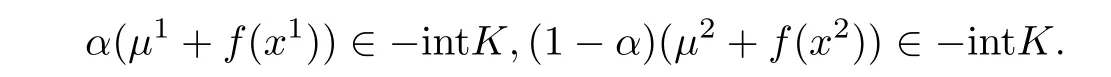
从而有
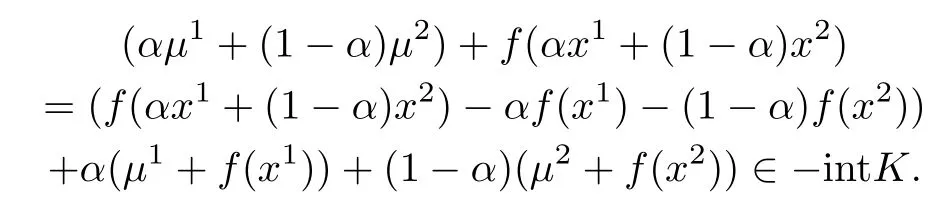
因此
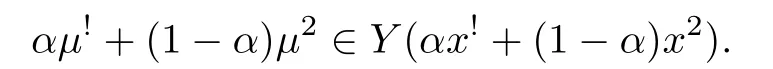
由于D为凸集,故

因此
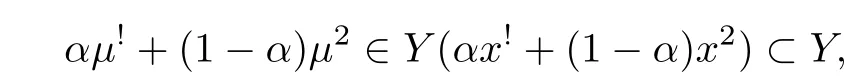
故Y为凸集.
下面用凸集分离定理证明本引理的结论.因为

无解,故0 /∈Y .因为Y为凸集,由凸集分离定理,存在λ∈Rp{0},使得∀µ∈Y,有
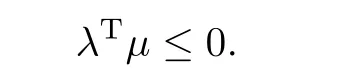
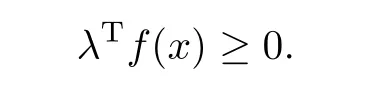
证记
由于∀¯µ∈-intK,∀α>0和∀x∈D有
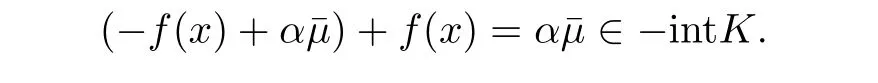
故
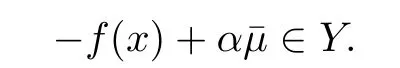
因此,∀α>0有

即∀α>0有

因此必有

即

故

在(7)式中令α→0,得知∀x∈D,有

引理3.3(广义Farkas引理)设C是Rn的凸子集,F : C→R是在C上的凸函数.同时假设
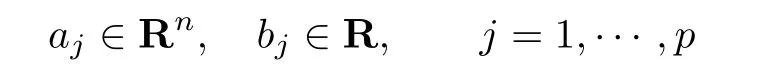
分别为给定的向量和标量.设A =(a1,···,ap),b =(b1,···,bp)T,K⊂Rp为闭凸锥,
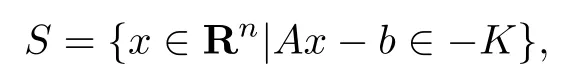
若S∩riC /=∅以及∪λ∈K∗epi(λTG)∗是Rp×R中的闭集,其中
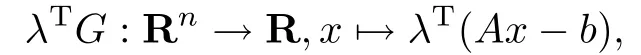
并且F(x)≥0,∀x∈S∩C.则存在µ∈K∗,使得
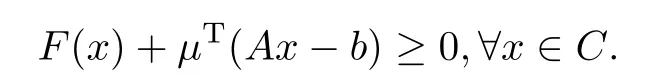
证考虑Rn×R的凸子集A1和A2,定义如下:

利用假设条件∀x∈S∩C都有F(x)≥0,可知A1和A2不相交,而A1是凸集且ri(A1)/=∅,A2是一个闭凸集.因此,根据文[12]的命题3.5.1,存在向量(ξ,β)∈{Rn×R}{0},使得
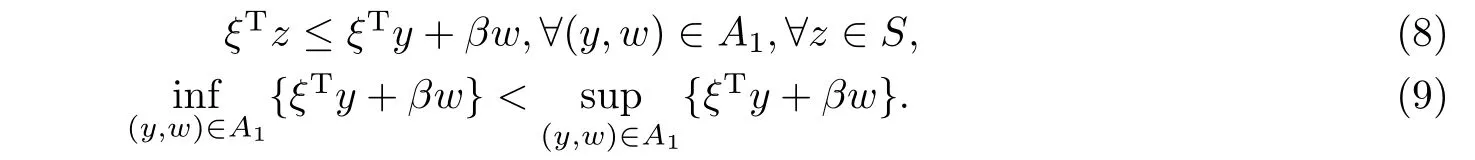
根据A1的定义,可知β≥0,否则(8)式的右边就可以减少到负无穷.现在证明β>0.采用反证法,假设β= 0.令¯x∈S∩riC,令¯w满足(¯x,¯w)∈A1,由(8)可得
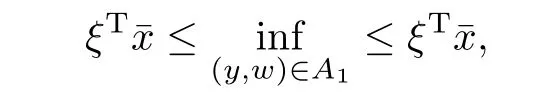
从而线性函数ξTy在A1上的最小值可以在点(¯x,¯w)取得,且由于¯x∈riC,故点(¯x,¯w)是A1的一个相对内点.因此,根据文[13]的命题B.19(a),ξTy在A1上是常数,但这与(9)式矛盾,这一矛盾是由β= 0的假设引起的.因此,必有β>0,且通过将(ξ,β)归一化,可以假设β= 1 .
利用S的定义及(8)式,得到

由于S非空,上式左边的线性规划问题具有有限的最优值,故该问题具有最优解x∗.

即
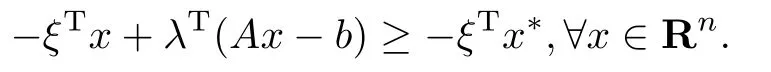
由上式可得
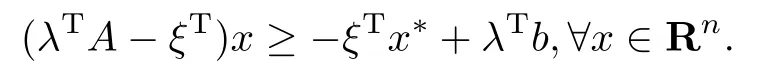
因此,
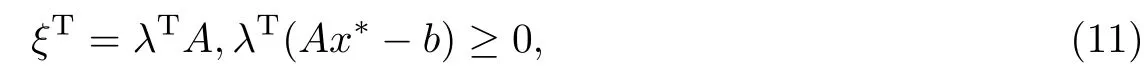
因为λ∈K∗,Ax∗- b∈-K,所以

结合(11)式和(12)式,得到

由(11)式和(13)式得

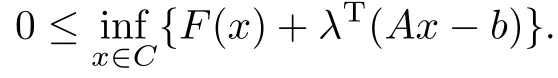
这就证明了所需要的结论.
定理3.1若x∗是(MPP)的K-弱有效解,g在x∗处满足广义Abadie约束条件,ϕ是Rn上有限值K-凸函数,并且对任意的如果中的闭集,其中,那么存在λ∈使得

证由引理3.1,知
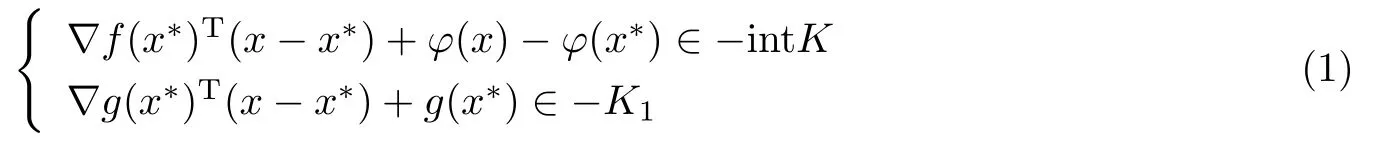
在riC内无解.显然Z(x∗)∩riC是非空凸集,由引理3.2,知存在λ∈K∗{0},使得
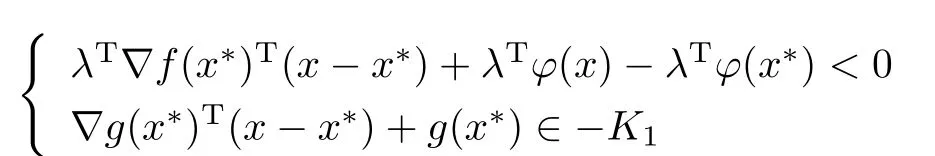
在riC内无解.由引理3.3,知存在µ∈K∗1,使得
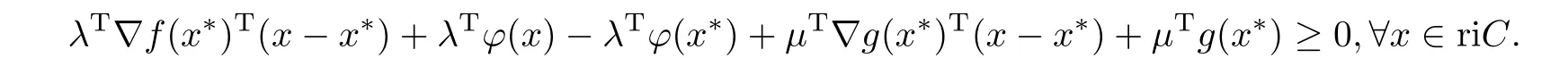
因为riC /=∅且C为凸集,所以

在(17)式中,令x = x∗,则有µTg(x∗)≥0.又因为

从而有
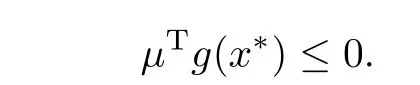
所以,µTg(x∗)= 0,于是(16)式成立,代入(17)式,有
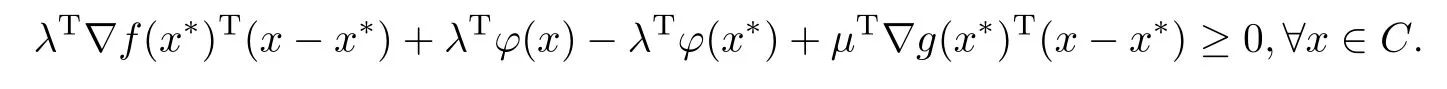
即

从而(15)成立.定理得证.
考虑下列的问题:
(MPP1)
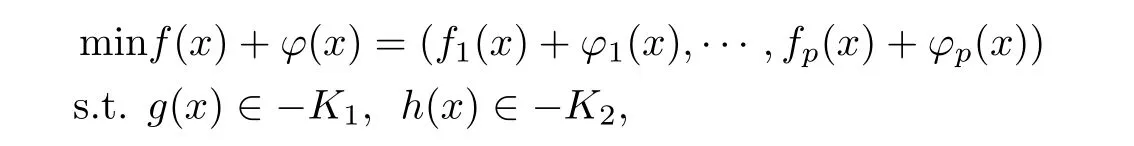
其中
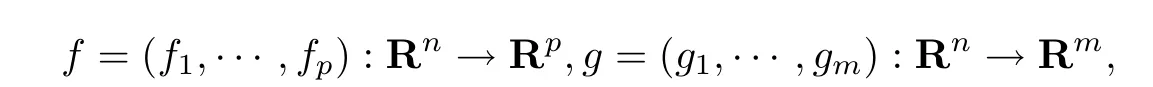
f和g是Rn上上的可微多目标函数,ϕ(x)=(ϕ1,···,ϕp): Rn→Rp是Rn上有限值K-凸函数,h =(h1,···,hr): Rn→Rr是Rn上有限值K2-凸函数;K,K1,K2分别是Rp,Rm,Rr的尖闭凸锥且intK /=∅,intK1/=∅,intK2/=∅.
定理3.2若x∗是(MPP1)的K-弱有效解,g在x∗处满足广义Abadie约束条件,ϕ是Rn上有限值K-凸函数,h是Rn上有限值K2-凸函数,并且对任意的x,y∈Rn有

如果Z(x∗)∩{x∈Rn|h(x)∈-intK2}/=∅,∪λ∈K∗epi(λT¯G)∗是Rp×R中的闭集,其中

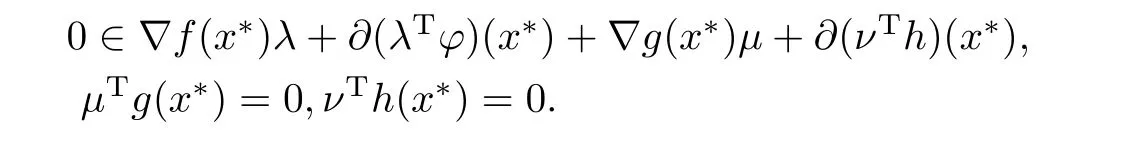
证设

由条件
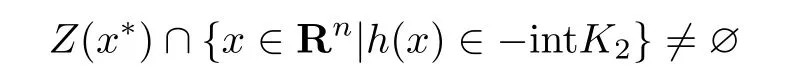
知{x∈Rn|h(x)∈-intK2}/=∅.又有K2是Rp的尖闭凸锥且intK2/=∅,容易证明
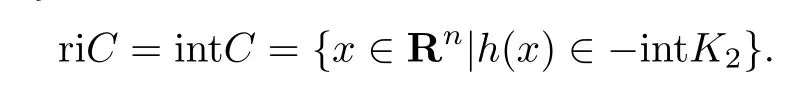
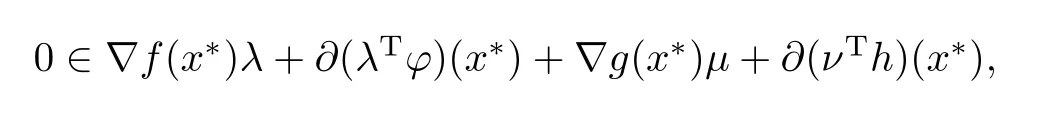
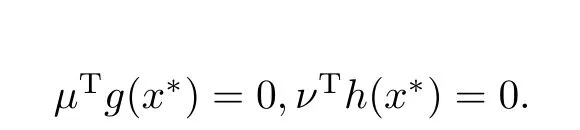
中的闭集”,是广义Farkas引理成立的正则性条件,有时称为“闭锥条件”,该条件在文[14-19]均有详细讨论.在无限维空间中,该条件为“是弱*闭的”.特别地,在有限维空间中,当¯G是Rn→ Rp的线性映射显然是闭集.因此,在有限个不等式约束条件中,“闭锥条件”自然成立.
注3.2在定理3.1中用到的条件“Z(x∗)∩riC /=∅”,即不等式

在riC中有解.因为C是凸集,所以riC /=∅.例如:设
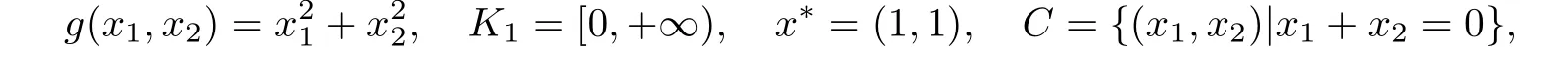
则

显然Z(x∗)∩riC = C /=∅.文[10]和文[11]都用到了条件“Z(x∗)∩riC /=∅”,文[13]在第507-510页上详细讨论该条件的必要性.
[1]Yang Xinmin,Yang Xiaoqi,Teo K L. Higher-order generalized convexity and duality in nondifferentiable multiobjective mathematical programming[J]. J Math Anal Appl,2004,297: 48-55.
[2]Bae D B,Kim D S. Optimality and duality theorems in nonsmooth multiobjective optimization[J]. Fixed Point Theory and Appl,2011,2011: 42.
[3]Mond B. A class of nondifferentiable mathematical programming problems[J]. J Math Anal Appl,1974,46: 169-174.
[4]Mond B,Schechter M A. On a constraint qualification in a nonlinear programming problems[J]. New Res Logic Quart,1976,23: 611-613.
[5]Aggarwal S A,Saxena P C. A class of fractional functional programming problems[J]. New Zealand Oper Res,1979,7: 79-90.
[6]Singh C. Optimality conditions for fractional minimax programming[J]. J Math Anal Appl,1984,100: 409-415.
[7]Lai Hangchin,Liu Jianchuan,Tanaka K. Necessary and sufficient conditions for minimax fractional programming[J]. J Math Anal Appl,1999,230: 311-328.
[8]Luo Hezhi,Wu Huixian. K-T necessary conditions for a class of nonsmooth multiobjective programming[J]. OR Transactions,2003,7: 62-68.
[9]Mangsarian O L. Nonlinear Programming[M]. New York: McGraw-Hill Book Company,1969.
[10]Xu Zengkun. Constraint qualifications in a class of nondifferentiable mathematical programming problems[J]. J Math Anal Appl,2005,302: 282-290.
[11]Wu Huixian and Luo Hezhi. Necessary optimality conditions for a class of nonsmooth vector optimization problems[J]. Acta Math Appl Sinica(English Series),2009,25(1): 87-94.
[12]Bertsekas D P,Nedi´c A,Ozdaglar A E. Convex Analysis and Optimization[M]. Belmont,MA:Athena Scientific,2003.
[13]Bertsekas D P. Nonlinear Programming,2nd Ed.[M]. Belmont,MA:Athena Scientific,2004.
[14]Jeyakumar V,Lee G M. Complete characterizations of stable Farkas'lemma and coneconvex programming duality[J]. Math Prog,Ser A,2008,114: 335-347.
[15]Bot R I,Wanka G. An alternative formulation for a new closed cone constraint qualification[J]. Nonlinear Anal Theory Methods Appl,2006,64(6): 1367-1381.
[16]Dinh N,Jeyakumar V,Lee G M. Sequential Lagrangian conditions for convex programs with applications to semidefinite programming[J]. J Optim Theory Appl,2005,125: 85-112.
[17]Gwinner J. Results of Farkas type[J]. Numer Funct Anal Optim,1987,9: 471-520.
[18]Jeyakumar V,Lee G M,Dinh N. Characterization of solution sets of convex vector minimization problems[J]. Eur J Oper Res,2006,174: 1380-1395.
[19]Gwinner J,Pomerol J C. On weak* closedness,coerciveness,and inf-sup theorems[J]. Arch Math,1989,52: 159-167.
MR Subject Classification: 90C32
Optimality conditions for a class of nonsmooth multi-objective programming problems
ZHOU Xuan-wei
(Dept. of Basic Courses,Zhejiang Shuren Univ.,Hangzhou 310015,China)
In this paper,a class of nonsmooth multi-objective programming problems is studied. By using generalized Farkas lemma and scalarization of multi-objective function,the optimality conditions of cone weakly efficient solution are given for the problem of minimizing a multi-objective function,where the multi-objective function is the sum of a differentiable multi-objective function and a cone convex multi-objective function,subject to a set of differentiable nonlinear functions with a controlled cone on a convex subset of a finite dimensional Euclidean space,under the conditions similar to the Abadie constraint qualification.
nonsmooth multi-objective programming;generalized Abadie constraint qualification;generalized Farkas lemma;optimality conditions
A
1000-4424(2016)01-0063-10
2015-10-08
2016-01-19

