基于双重混合粒子群算法的配电网重构

马草原　孙展展　尹志超　刘建华　李春晓

(1.中国矿业大学信息与电气工程学院　徐州　221116 2.中国矿业大学江苏省煤矿电气与自动化工程实验室　徐州　221116)

基于双重混合粒子群算法的配电网重构

马草原1，2孙展展1，2尹志超1，2刘建华1，2李春晓1，2

(1.中国矿业大学信息与电气工程学院徐州221116 2.中国矿业大学江苏省煤矿电气与自动化工程实验室徐州221116)

摘要为进一步优化配电网运行结构，将混合蛙跳思想引入粒子群算法，结合配电网结构简化、支路分组，提出一种基于双重混合粒子群算法的配电网重构策略。为提高粒子搜索效率、防止算法早熟，首先，等效简化配电网结构图，对支路分组，缩短编码维数；其次，将各粒子依据一定规则分组，采用基于混合蛙跳思想的二进制粒子群算法进行支路组搜索，且对粒子历史最优值进行多次分组，组内搜索采用二进制粒子群搜索算法。运用该方法分别对IEEE33节点配电系统和136节点配电系统进行仿真，并与遗传算法和粒子群遗传混合算法进行对比分析，结果表明该方法收敛速度快，可得到最优网络重构结果，有效降低网损。

关键词：配电网重构混合蛙跳思想双重混合粒子群算法组内二进制粒子群搜索算法

0引言

配电网是联系高压输电网和负荷的重要枢纽，配电网重构则是配电管理系统的重要组成部分[1，2]。它是指在满足一定约束条件下，通过改变开关组合状态、调整运行结构，达到降低网损、消除过载、平衡负荷和提高电能质量等目的[3-6]。

配电网重构可有不同的优化目标，如以网损最小为主的经济性优化目标，以提高用户供电质量的安全性优化目标等，且可以将不同优化目标相结合进行多目标的重构优化[7-9]。

配电网重构本质上是一个多目标非线性混合优化问题，在数学上，是一种NP难问题[10]。目前，专家学者所采用的求解方法主要有基于数学优化理论的重构算法、基于启发式的重构算法和随机组合优化算法[11]。文献[12]采用一种动态优化算法，减小组合数，缩短搜索时间，提高效率。文献[13，14]通过改进最优流模式算法，减少搜索过程中的计算量，提高寻优速度。文献[15]依据网络实际情况，改善遗传算法中染色体编码方式，缩小搜索空间，提高寻优效率。文献[16]采用遗传算法和启发式算法相结合的混合算法，通过编码策略的改进，大幅提高搜索效率。文献[17]将遗传算法和模拟退火算法相结合用于配电网重构中。文献[18]提出一种结合变异运算的禁忌搜索算法，增强跳出局部最优的能力，提高了全局搜索能力和搜索效率。此外，还有基于智能优化方法的配电网重构算法，包括人工神经网络、专家系统、模糊数学等。人工神经网络可以节省重构时间，但精度依赖于训练样本，且获取完整样本比较困难，限制了实用性。专家系统和模糊数学理论基础理论差，处理时间长，且不能保证得到全局最优解。

粒子群优化算法(Particle Swarm Optimization，PSO)基于原理简单、鲁棒性强和易于实现等特点[19]，已广泛应用到配电网重构优化中。文献[20]采用混合粒子群算法进行配电网重构，缩短编码维数，减少不可行解的产生，提高搜索效率。文献[21]结合网络特点，改进粒子位置的更新规则，提高迭代过程中有效解的产生概率，并结合禁忌搜索算法，克服了PSO算法的早熟问题。文献[22]针对预防性控制提出一种混合粒子群算法，采用无不可行解的编码规则，既提高了搜索速度又有助于搜索到全局最优解。

本文根据配网结构特点，简化网络结构，以提高搜索效率，在粒子搜索过程中为尽量避免优化算法陷入局部最优解，在标准BPSO(Binary Particle Swarm Optimization)的基础上引入混合蛙跳思想，提出双重混合粒子群算法，以进行配电网网络结构优化，实现网络开关的最优组合。

1配电网重构的目标函数

配电网重构的目标函数具有多样性，可改善系统经济性、提高供电安全性，也可构建多目标函数。本文以配电网线路损耗f最小为目标函数

(1)

式中，i为支路编号；Ki为开关状态变量；Ri为支路i上的电阻值；Pi、Qi分别为支路i的有功功率和无功功率；Ui为支路i前端节点的电压。

配电网重构除需满足潮流方程约束外，还需满足电压约束、电流约束、线路容量约束和网络结构辐射状运行约束等，如

(2)

式中，Ui、Uimin、Uimax分别为节点i的电压、电压下限和上限；Ii、Iimax、Iimin分别为支路i的电流及电流上下限；Si和Simax分别为各线路i流过的功率和其最大容许值；gk为迭代之后的网络结构；G为辐射状网络结构集合。

2标准粒子群优化算法

PSO是由J.Kennedy和R.Eberhart博士在1995年提出的，源于对鸟群觅食过程的模拟，是一种基于社会群体行为的全局优化算法[23-25]。影响粒子当前速度的因素主要有3个：前代速度、个体认知部分和社会学习部分。粒子在寻优过程中根据自身惯性速度、自身历史最优位置和种群历史最优位置对速度进行调整，改变它们的飞行速度和方向，最终达到空间最优位置。标准粒子群优化算法的速度和位置更新公式为

(3)

标准二进制粒子群优化算法将粒子位置的每维分量定义为0或1，通过Sigmoid函数把粒子速度表示为粒子位置每位取值为1的概率，其速度矢量更新公式不变。Sigmoid函数式为

(5)

(6)

式中，vjm∈ [vmin,vmax]，vmax和vmin分别为粒子每维速度上下限值。

3配电网结构简化

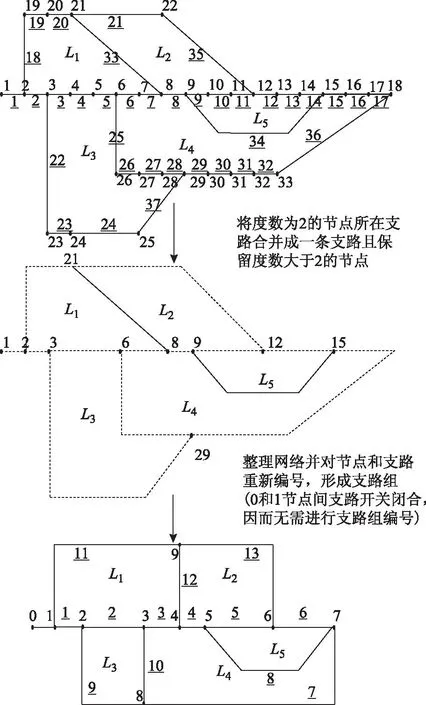
图1　配电网化简示意图Fig.1　Process of the simplifying of distribution network

配电网重构时由于粒子位置每维分量取0或1具有随机性，会产生不满足网络结构约束条件的大量无效解。因此，降低粒子编码维数，简化网络结构，提高寻优效率是必要的。根据文献[20]所提方法对网络进行简化，简化原则为：将度数为2的节点所属支路合并成一条支路形成支路组，并进行编号，度数大于2的节点保留。图1为算例IEEE33节点网络结构图的简化过程，可见每个支路组包含多条支路，如支路组6包括支路12-13、13-14、14-15。这样，就大大降低了编码维数，解矢量由原来的37维简化为13维，减少了大量无效解的产生，提高了算法寻优效率。

另外，在配电网重构中，设支路组数量为M，则支路组间的优化编码维数为M，每个粒子编码都是由0、1组成的矢量，代表配电网的一种拓扑结构。且要求粒子编码要满足支路组断开数目N-CS等于支路组总数减去有效节点数(属于支路组的有效节点)再加1，如下公式

N-CS=支路组总数-有效节点数+1

(7)

这样，重构过程中断开的支路组数是确定的，即等于该网络中含有的环网，在此基础上断开所选各支路组中的任意一条支路，必属于不同的支路组，避免再次进行支路组合可行解的分析，可以减少无效解的产生，提高搜索效率。

4双重混合粒子群算法及其应用

在配电网结构简化的基础上，配电网要完成一次满足约束条件和必要条件的重构，需要进行支路组选择优化、支路组选择的可行性分析、支路组内部支路选择优化和潮流计算，这4部分之间的关系可用图2表示。支路组选择优化和支路组内部支路选择优化分别采用基于混合蛙跳思想的二进制粒子群算法和组内二进制粒子群搜索算法，统称双重混合粒子群算法。支路组选择的可行性分析采用文献[26]中的方法，配电网潮流计算采用基于节点分层矩阵的前推回代法[27]。

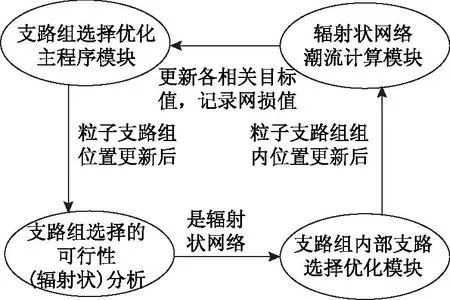
图2　模块间关系Fig.2　Module diagram

4.1基于混合蛙跳思想的二进制粒子群算法

混合蛙跳思想[28，29]是指在湿地里生活着一群青蛙，每只青蛙代表问题的一个解，由于每只青蛙跳跃方向不同，这群青蛙被分为若干子群，不仅子群内个体相互学习，而且在一定时间内各子群间也相互学习、交流信息，每只青蛙充分利用子群和种群的信息来寻找食物。如设初始种群个体N=20，即(x1,x2,x3,…,x20)，依据初始适值应度大小进行排序，将种群分为4个子群，每个子群包含5个粒子(青蛙)，即组1、组2、组3、组4分别为(x3,x16,x7,x9,x14)、(x1,x4,x8,x10,x13)、(x6,x19,x11,x12,x17)、(x15,x5,x2,x18,x20)，之后种群不再分组，但各子群中各粒子历史最优位置在组内搜索迭代一定次数后进行分组，作为相应各组粒子的历史最优位置。粒子的迭代方式在标准二进制粒子群上增加对各小组最优粒子信息的利用，使各小组利用不同的迭代公式进行进化，保证了粒子间的差异性，体现了各粒子所搜索到的最优位置不仅对自身有指导作用，而且还对其他粒子的搜索轨迹具有一定的指导作用。

基于混合蛙跳思想的二进制粒子群算法是在标准二进制粒子群算法的基础上引入混合蛙跳思想，且对惯性系数w进行正弦调整，改进其速度更新公式而得。改进后二进制粒子群算法速度迭代公式为

(8)

(9)

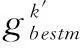
4.2支路组组内二进制粒子群搜索算法

以IEEE33节点配电系统为例，首先确定支路组序号×组内支路编号矩阵A(将支路组与支路组组内支路关系用矩阵表示主要是为简化编程和潮流计算代码)，支路组组内优化时，最优断开支路变量为整数，如矩阵A中非零元素，其元素所在列表示该支路所在支路组内的编号，为运用二进制粒子群算法进行支路组组内搜索，须将每个支路组组内支路的断开或闭合用0或1表示，且每个支路组组内仅有一个支路断开，因此，需设定各支路组对应矢量Ai(包括A1～A13)，也就是支路组组内各支路位置，如式(10)所示。在第一步已得搜索断开支路组序号的基础上，进行组内断开支路选择，在支路组组内选择优化时也引入混合蛙跳思想，下面给出支路组组内二进制粒子群搜索算法速度更新公式，如式(11)所示，位置更新公式不变。

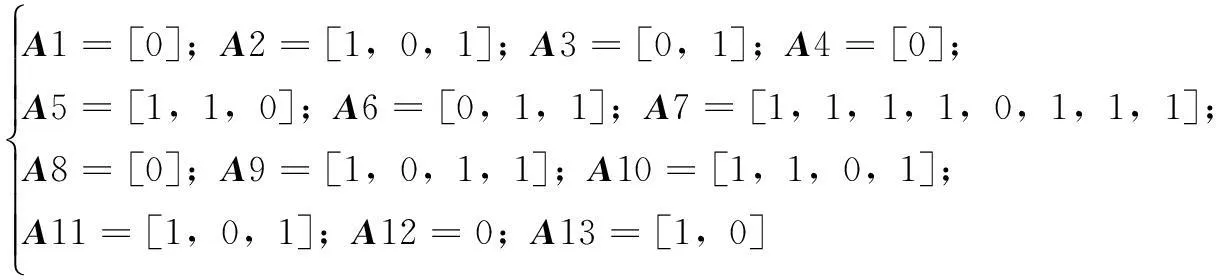
(10)

(11)

针对式(11)，设在改进二进制粒子群算法进行支路组选择优化时，若粒子i支路组位置第m维被选中置0，即第m个支路组被选中断开，则在支路组内选择优化过程中分为以下两种情况：①当个体历史最优值、群体历史最优值和粒子组内种群历史最优值的支路组位置第m维为0时，则对支路组位置是0状态的被优化粒子的支路组组内支路更新具有导向作用，保留相关项，对应式(11)中的第一种情况；②其余情况则遵循：只要历史最优值的第m维为0，则对优化粒子都具有导向作用，否则没有导向作用，删除对应项。若粒子i支路组位置第m维置1，即第m个支路组闭合，则无论个体历史最优值、群体历史最优值、粒子组内种群历史最优值的支路组位置第m维为何值，其相应支路组组内的支路位置不做更新。

基于混合蛙跳思想的二进制粒子群算法和支路组组内二进制粒子群搜索算法是配电网重构优化过程中的核心程序模块，两者具有前后、上下层次关系，缺一不可。首先通过基于混合蛙跳思想的二进制粒子群算法进行支路组选择优化，然后再通过组内二进制粒子群搜索算法进行组内支路选择优化。配电网重构算法的流程如图3所示，具体步骤如下：

1)设定粒子种群个数N、种群组数及其他各参数。

2)依照网络结构简化原则，化简配电网结构。对节点、支路组重新编号，支路组内部支路编号如矩阵A中元素的列号，并根据实际问题确定粒子支路组维数D和各支路组组内维数DD(不同支路组组内维数不一定相同)，初始化种群支路组位置、速度和每个支路组组内位置和速度，计算每个粒子的适应度值，并进行排序分组。

3)将粒子历史最优适应度值由小到大进行排序，并对粒子历史最优适应度值进行分组，得到全局最优值及各组内最优值。

4)依据式(6)和式(8)更新支路组速度和位置，配电网结构若为辐射状，则进行下一步，否则，重复该步骤。

5)依据式(6)和式(11)更新支路组组内断开支路位置，并依据矩阵A查找潮流计算中实际断开支路编号，并计算其适应度值。

6)将粒子更新后的适应度值与粒子历史最优适应度值及粒子群最优适应度值进行比较，如果更好，则将其作为粒子的个体历史最优值和粒子群最优值，用当前位置更新个体历史最好位置和粒子群历史最好位置。同理，调整种群各组内粒子最优值和粒子位置。

7)未达到组内迭代次数，转到步骤5。

8)达到组内迭代次数后，各组更新后的粒子历史最优值进入下一次分组，转到步骤3。

9)达到分组次数后，输出重构优化结果，退出。

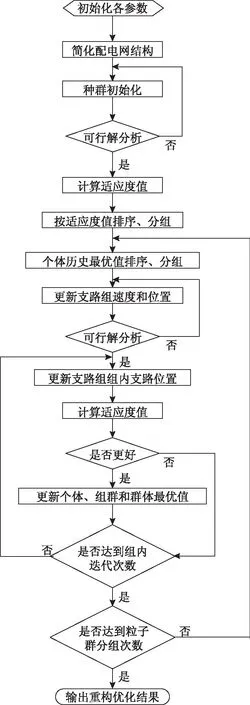
图3　配电网重构算法流程Fig.3　The flow chart of distribution network reconfiguration algorithm

5算例

以两个算例进行仿真。算例1是IEEE33节点配电网络，结构如图1中的原始图。该配电系统包含33个节点和37条支路，5个联络开关，基准电压为12.66 kV，总负荷为3 715+j2 300 kV·A。

CM教科书的例题一般分为“例题（examples）”“现实世界举例（real-world example）”两个模块．有理数章节“例题”模块下的题目是概念理解或运用法则的计算类基础题．“现实世界举例”模块下的例题均是与实际生活相关的应用题，该模块的特别之处在于每个例题旁边都会附有实景插图和相关背景的介绍来丰富学生的认知（如图9）．

该网络N-CS=5，对支路进行简化分组，共分为13个支路组即D=13，分组情况如式(10)矩阵A。设定粒子种群N=20，粒子组数为4，粒子历史最优值分组次数T1=MaxIterance=20，组内迭代次数T2=4，共进行80次迭代，w1=1.2，w2=0.8，c1=c2=c3=c11=c12=c13=2。潮流计算采用基于节点分层的配电网潮流前推回代方法，收敛条件为前后迭代两次电压差的模值最小值小于0.000 001。表1为配电网重构前后的结果对比。

表1　配电网重构结果

由表1可见，重构后网络有功损耗为139.47 kW，小于重构前网络有功损耗202.65 kW，减少了31.18%，降低了线路损耗，提高了配电网络的经济性，另外，节点最低节点电压从0.913 3(pu)增加到0.937 8(pu)，系统的稳定性得到增强。

从图4中可以看出重构后网络节点电压整体上普遍高于重构前网络节点电压，显然系统的稳定性得到整体提高。另外，将本文算法重构结果与改进禁忌搜索算法[30]、粒子群和遗传混合算法[31]、遗传和禁忌搜索混合算法[32]以及混沌二进制粒子群算法[33]的重构结果相比较，见表2。可以看出利用本文提出的双

图4　网络重构前后各节点电压对比Fig.4　Comparison chart of node voltage before and after network reconfiguration

表2　与其他算法对比

重混合粒子群算法进行网络重构后的网损较低，最低节点电压与其他算法相差无几，表明了该算法的有效性。

图5对比遗传算法(GA)、粒子群遗传混合算法(PSO-GA)，给出了网损收敛曲线随迭代次数的变化趋势。可以看出，遗传算法和粒子群遗传混合算法在迭代次数达到15次左右时网损收敛，本文算法在分组迭代次数接近12次左右时，种群历史最优值就达到139.47 kW，优于其他两种算法，表明本文算法能够快速跳出局部最优，防止算法早熟，寻求到全局最优值。

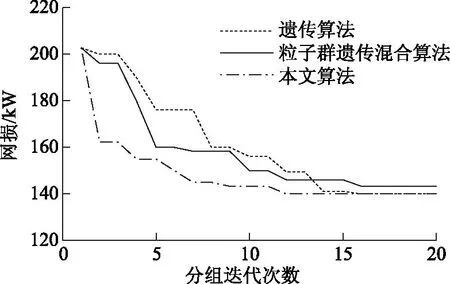
图5　网损收敛曲线对比Fig.5　Loss convergence curve comparison chart

算例2是136节点真实配电系统，电压等级为10 kV，总负荷为18.016 5+j7.611 0 MV·A。该配电系统共有135条支路，无联络开关，网络中最大电阻为1.56 Ω，现给该网络添加7条联络开关，拓扑结构如图6所示，图中虚线为联络开关，初始结构断开联络开关。依据算例1对其进行网络化简和参数设置，重构前线路有功损耗为283.52 kW，最低节点电压为0.933 1(pu)；重构后线路有功损耗为162.95 kW，减少43.53%，最低节点电压为0.962 2(pu)，断开支路为58-59、41-49、61-70、45-71、91-112、41-56、40-63，重构20次，平均迭代次数14次，收敛曲线如图7所示，粒子群在分组迭代次数13次左右时收敛，可见随着网络规模的增大，其计算时间有所增长，收敛迭代次数变化不大，在可接受范围内，表明该算法适用性较强。

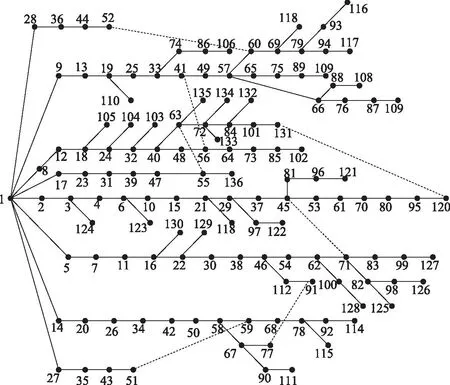
图6　136节点拓扑结构Fig.6　Topology map of 136 nodes

图7　网损收敛曲线对比Fig.7　Loss convergence curve comparison chart

图7为本文提出的双重混合粒子群算法、GA和PSO-GA的网损收敛曲线对比图。从图中可以看出，该算例在GA下重构迭代次数在17次左右收敛且网损收敛值在200 kW左右，高于本文算法迭代次数和网损收敛值，在PSO-GA下搜索时间有所减少，迭代次数为15次，收敛值同遗传算法收敛值，依然不理想。可见，双重混合粒子群算法能较快地搜索到全局最优值，但需要进一步提高收敛速度，与其他先进改进算法进行对比分析、综合优化，使其性能达到最优。

6结论

本文是以降低网损为目标函数的配电网重构，在简化网络结构、缩短编码维数的基础上，引入混合蛙跳思想，提出了双重混合粒子群算法，利用基于混合蛙跳思想的二进制粒子群算法进行支路组间的搜索，组内搜索采用支路组组内二进制粒子群搜索算法。采用本文方法进行算例仿真计算，得到如下结论：

1)对比分析GA和PSO-GA，本文算法具有更快的寻优速度，可快速有效地降低系统网损，提高网络节点最低电压，优化配电网运行结构，对解决配电网重构问题具有一定的指导意义和实际应用价值。

2)在大规模配电系统中，粒子收敛速度会减小，搜索时间有所增加，搜索结果目标函数值也会因初始赋值随机性的原因而有所波动。因此，如何避免不可行解的产生以及如何将专家经验引进到群体初始赋值过程中，进一步提高算法收敛速度和稳定性以实现多目标函数的配电网重构，将是下一步待研究的内容。

参考文献

[1]Merlin A，Back H，Merlin A，et al.Search for a minimal-lossoperatingspan-ning tree configuration for anurbanpower distributionsystem[C]//Fifth Power Systems Computer Conference，Cambridge，1975，1：2-6.

[2]张涛，史苏怡，俆雪琴.基于二进制量子粒子群算法的含分布式电源配电网重构[J].电力系统保护与控制，2016，44(4)：23-28.

Zhang Tao，Shi Suyi，Xu Xueqin.Distribution network reconfiguration with distributed generation based on improved quantum binary particle swarm optimization[J].Power System Protection and Control，2016，44(4)：23-28.

[3]田昊，吕林，高红均，等.计及电网运行特性的配电网动态重构[J].电力系统保护与控制，2015，43(1)：10-14.

Tian Hao，Lü Lin，Gao Hongjun，et al.Dynamic reconfiguration of distribution network considering power grid operation characteristic[J].Power System Protection and Control，2015，43(1)：10-14.

[4]陈春，汪沨，刘蓓，等.一种避免不可行解的配电网快速重构方法[J].电工技术学报，2015，30(7)：35-42.

Chen Chun，Wang Feng，Liu Bei，et al.A fast network reconfiguration method avoiding infeasible solutions for distribution System[J].Transactions of China Electrotechnical Society，2015，30(7)：35-42.

[5]葛少云，刘自发，余贻鑫.基于改进禁忌搜索的配电网重构[J].电网技术，2004，28(23)：22-26.

Ge Shaoyun，Liu Zifa，Yu Yixin.An improved tabu search for reconfiguration of distribution systems[J].Power System Technology，2004，28(23)：22-26.

[6]靳晓凌，赵建国.基于改进二进制粒子群优化算法的负荷均衡化配电网重构[J].电网技术，2005，29(23)：40-43.

Jin Xiaoling，Zhao Jianguo.Distribution network reconfiguration for load balancing based on improved binary particle swarm optimization[J].Power System Technology，2005，29(23)：40-43.

[7]孙惠娟，彭春华，袁义生.综合开关次数分析的配电网多目标动态重构[J].电力自动化设备，2014，34(9)：41-46.

Sun Huijuan，Peng Chunhua，Yuan Yisheng.Multi-objective dynamic distribution network reconfiguration considering switching frequency[J].Electric Power Automation Equipment，2014，34(9)：41-46.

[8]彭锦新.配电网络多目标最优重构研究[D].成都：四川大学，2005.

[9]李奔，刘会家，李珺.考虑网络结构优化的含风电配电网多目标重构[J].电力系统保护与控制，2015，43(17)：58-62.

Li Ben，Liu Huijia，Li Jun.Multi-objective reconfiguration of distribution network with wind power generators considering network survivability[J].Power System Protection and Control，2015，43(17)：58-62.

[10]余贻鑫，段刚.基于最短路算法和遗传算法的配电网络重构[J].中国电机工程学报，2000，20(9)：44-49.Yu Yixin，Duan Gang.Distribution network reconfiguration based on shortest path algorithm and genetic algorithm[J].Proceedings of CSEE，2000，20(9)：44-49.

[11]赵金利，于莹莹，李鹏，等.一种基于锥优化的DG 优化配置快速计算方法[J].电工技术学报，2014，29(12)：174-179.

Zhao Jinli，Yu Yingying，Li Peng，et al.A fast determination method of DG capacity in distribution network based on conic programming[J].Transactions of China Electrotechnical Society，2014，29(12)：174-179.

[12]刘伯私，谢开贵，周家启.配电网重构的动态规划算法[J].中国电机工程学报，2005，25(9)：29-35.Liu Bosi，Xie Kaigui，Zhou Jiaqi.Dynamic programming algorithm of distribution network reconfiguration[J].Proceedings of CSEE，2005，25(9)：29-34.

[13]邓佑满，张伯明，相年德.配电网络重构的改进最优流模式算法[J].电网技术，1995，19(7)：47-50.

Deng Youman，Zhang Boming，Xiang Niande.An improved optimal flow pattern algorithm for distribution network reconfiguration[J].Power System Technology，1995，19(7)：47-50.

[14]吴本悦，赵登福，刘云，等.一种新的配电网络重构最优流模式算法[J].西安交通大学学报，1999，33(4)：25-28.

Wu Benyue，Zhao Dengfu，Liu Yun，et al.An improved optimal flow pattern algorithm for distribution network reconfiguration[J].Journal of Xi’an Jiaotong University，1999，33(4)：25-28.

[15]毕鹏翔，刘健，刘春新，等.配电网络重构的改进遗传算法[J].电力系统自动化，2002，26(2)：57-61.

Bi Pengxiang，Liu Jian，Liu Chunxin，et al.A refined algorithm for power distribution network reconfiguration[J].Automation of Electric Power Systems，2002，26(2)：57-61.

[16]Carreno E M，Romero R，Padilha-Feltrin A.An efficient codification to solve distribution network reconfiguration for loss reduction problem[J].IEEE Transactions on Power Systems，2008，23(4)：1542-1551.

[17]卢耀川，廖迎晨，陈星莺，等.基于遗传退火法的网络重构技术[J].电力自动化设备，2003，23(1)：28-31.

Lu Yaochuan，Liao Yingchen，Chen Xingying，et al.Distribution reconfiguration technology based on GA and SA[J].Electric Power Automation Equipment，2003，23(1)：28-31.

[18]张栋，张刘春，傅正财.基于改进禁忌算法的配电网络重构[J].电工技术学报，2005，20(11)：61-64.

Zhang Dong，Zhang Liuchun，Fu Zhengcai.Network reconfiguration in distribution systems using a modified TS algorithm[J].Transactions of China Electrotechnical Society，2005，20(11)：61-64.

[19]王振树，卞绍润，刘晓宇，等.基于混沌与量子粒子群算法相结合的负荷模型参数辨识研究[J].电工技术学报，2014，29(12)：212-217.

Wang Zhenshu，Bian Shaorun，Liu Xiaoyu，et al.Research on load model parameter identification based on the CQDPSO algorithm[J].Transactions of China Electrotechnical Society，2014，29(12)：212-217.

[20]李振坤，陈星莺，余昆，等.配电网重构的混合粒子群算法[J].中国电机工程学报，2008，28(31)：35-41.

Li Zhenkun，Chen Xingying，Yu Kun，et al.Hybrid particle swarm optimization of distribution network reconfiguration[J].Proceedings of CSEE，2008，28(31)：35-41.

[21]许立雄，吕林，刘俊勇.基于改进粒子群优化算法的配电网络重构[J].电力系统自动化，2006，30(7)：27-30.

Xu Lixiong，Lü Lin，Liu Junyong.Modified particle swarm optimizationof reeonfigurationof distribution network[J].Automation of Electric Power Systems，2006，30(7)：27-30.

[22]陈春，汪沨，黎灿兵，等.含分布式风电的配电网预防性重构[J].电工技术学报，2013，28(9)：173-177.

Chen Chun，Wang Feng，Li Canbing，et al.Preventive reconfiguration of distribution networks with distributed wind power[J].Transactions of China Electrotechnical Society，2013，28(9)：173-177.

[23]Kennedy J，Eberhart R.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks，Perth，WA，1995，4：1942-1948.

[24]苏海滨，高孟泽，常海松.基于粒子群算法的微电网有功无功下垂控制[J].电工技术学报，2015，30(1)：366-369.

Su Haibin，Gao Mengze，Chang Haisong.Microgrid droop control of active and reactive power based on PSO[J].Transactions of China Electrotechnical Society，2015，30(1)：366-369.

[25]程泽，董梦男，杨添剀，等.基于自适应混沌粒子群算法的光伏电池模型参数辨识[J].电工技术学报，2014，29(9)：246-252.

Cheng Ze，Dong Mengnan，Yang Tiankai，et al.Extraction of solar cell model parameters based on self-adaptive chaos particle swarm optimization algorithm[J].Transactions of China Electrotechnical Society，2014，29(9)：246-252.

[26]麻秀范，丁宁，李龙.配电网重构中网络辐射形与连通性的判断[J].电工技术学报，2014，29(8)：289-293.

Ma Xiufan，Ding Ning，Li Long.Judging radial and connectivity of network in distribution networks reconfiguration[J].Transactions of China Electrotechnical Society，2014，29(8)：289-293.

[27]李如琦，谢林峰，王宗耀，等.基于节点分层的配网潮流前推回代方法[J].电力系统保护与控制，2010，38(14)：64-66.

Li Ruqi，Xie Linfeng，Wang Zongyao，et al.Forward and backward substitution method of distribution network based on hierarchical node[J].Power System Protection and Control，2010，38(14)：64-66.

[28]黄太安，生佳根，徐红洋，等.一种改进的简化粒子群算法[J].计算机仿真，2013，30(2)：327-330.

Huang Taian，Sheng Jiagen，Xu Hongyang，et al.An improved simplified particle swarm algorithm[J].Computer Simulation，2013，30(2)：327-330.

[29]崔文华，刘晓冰，王伟，等.混合蛙跳算法研究综述[J].控制与决策，2012，27(4)：481-486.

Cui Wenhua，Liu Xiaobing，Wang Wei，et al.Survey on shuffled frog leaping algorithm[J].Control and Decision，2012，27(4)：481-486.

[30]董百强.基于禁忌搜索算法的配电网重构研究[D].重庆：重庆大学，2006.

[31]朱春涛.基于粒子群遗传混合算法的配电网重构研究[D].南京：南京理工大学，2012.

[32]梁栋.基于遗传和禁忌搜索算法的配电网重构[D].吉林：东北电力大学，2009.

[33]邓桂秀，江修波，蔡金锭.基于混沌二进制粒子群算法的配电网重构研究[J].电力科学与工程，2013，29(9)：34-37.

Deng Guixiu，Jiang Xiubo，Cai Jinding.Study of distribution network reconfiguration based on chaoticbinary particle swarm algorithm[J].Science and Engineering，2013，29(9)：34-37.

Reconfiguration of Distribution Network Based on Double Hybrid Particle Swarm Algorithm

Ma Caoyuan1，2Sun Zhanzhan1，2Yin Zhichao1，2Liu Jianhua1，2Li Chunxiao1，2

(1.School of Information and Electrical EngineeringChina University of Mining &Technology Xuzhou221116China 2.Jiangsu Province Laboratory of Electrical and Automation Engineering for Coal Mining China University of Mining &TechnologyXuzhou221116China)

AbstractTo further optimize the operation structure of the distribution network,by embedding the idea of mixing leapfrog in the particle swarm algorithm and combining with network structure simplification and branches grouping,this paper proposes a distribution network reconfiguration strategy based on the double hybrid particle swarm algorithm.In order to improve search efficiency and avoid algorithm premature,firstly,the network structure is simplified and decomposed into subsystems in order to reduce the coding dimension.Secondly,the particles are divided into different groups according to certain rules.A binary particle swarm optimization algorithm based on the idea of mixing leapfrog is used to search between groups;the historical optimal value wouldbe regrouped repeatedly;and a group binary particle swarm search algorithmproposed in this paper is used to search within the group.The proposed algorithm is tested on the IEEE33 nodes and 136 nodes distribution power system respectively,and compared with the genetic algorithm and a hybrid algorithm based on the genetic algorithm and the particle swarm algorithm.Simulation results illustrate that the proposed algorithm can determine the optimal configuration,which can significantly reduce system energy losses,with fast convergence rate.

Keywords：Distribution network reconfiguration，the idea of mixing leapfrog，double hybrid particle swarm algorithm，group binary particle swarm search algorithm

收稿日期2014-12-02改稿日期2016-03-26

作者简介E-mail：mcycumt@126.com(通信作者) E-mail：1261387305@qq.com

中图分类号：TM727

江苏省自然科学基金(BK20130187)、国家留学基金(201406425007)和江苏省煤矿电气与自动化工程实验室建设项目(中国矿业大学)(2014KJZX05)资助。

马草原男，1978年生，博士，副教授，研究方向为电气安全与智能电器。

孙展展男，1995年生，硕士研究生，研究方向为电力系统及其自动化。