基于序分量无功功率的单相自适应重合闸

罗勋华　黄　纯　潘志敏　刘　琨　梁勇超

(1.湖南大学电气与信息工程学院　长沙　410082 2.湖南省电力公司检修公司　长沙　410004)

基于序分量无功功率的单相自适应重合闸

罗勋华1黄纯1潘志敏2刘琨2梁勇超2

(1.湖南大学电气与信息工程学院长沙410082 2.湖南省电力公司检修公司长沙410004)

摘要针对不带并联电抗器的超高压输电线路，提出一种基于序分量无功功率的单相自适应重合闸实现方法。当线路发生单相接地故障且故障相两端断路器跳开后，在永久性故障下，线路侧各相电压和电流值经短暂时间过渡到稳态，之后各序分量无功功率基本保持恒定；在瞬时性故障二次电弧尚未熄弧阶段，电弧电压和故障相端电压随电弧拉长不断升高，正序无功与负序无功呈现相反方向的增减变化。基于这一现象，采用线路侧断开处的正序与负序无功功率分量的变化率来区别永久性和瞬时性故障。在二次电弧熄弧瞬间，故障相电压相位会后移90°，此时正序与负序无功功率分别有不同极性的跃变，通过检测序分量无功功率的突变来捕捉熄弧时刻。该方法实现简单，耐过渡电阻能力强，受故障位置影响小，能适用于重负载线路。EMTP仿真验证了其正确性和有效性。

关键词：输电线路单相自适应重合闸故障电弧序分量无功功率

0引言

统计表明，80%以上的高压架空线路故障为单相接地故障，其中由电弧引起的瞬时性故障占绝大多数。单相自动重合闸能有效提高电力系统运行稳定性，被广泛应用于高压输电系统中。但目前输电线路大多采用固定时间间隔重合方案，当重合于永久性故障或瞬时性故障二次电弧阶段，将造成重合闸失败，给电力系统带来严重的二次冲击。针对传统重合闸的这一问题，研究人员提出了自适应单相重合闸技术，如何识别故障性质和捕捉二次电弧熄弧时间是实现自适应单相重合闸的关键。

高压架空输电线路分为带并联补偿电抗器和不带并联电抗器两种。国内学者针对前者研究较多[1-7]，而短距离输电线路大部分没有安装并联电抗器，国外文献研究较多。对于不带并联补偿电抗器的输电线路，其自适应重合闸方法已有多种[8-18]。研究最多的是电压判据法[8，9]，该方法利用恢复电压中所含耦合电压的不同区分瞬时性与永久性故障，其主要不足是耐过渡电阻能力低，在重负载线路下灵敏度降低。受二次电弧电阻非线性的影响，电弧电压波形严重畸变，使得故障相端电压谐波含量很高。基于此现象，文献[10]利用奇次谐波的衰减速度及其能量百分比在不同故障性质下随时间的变化规律来区别故障性质。文献[11]根据故障相端电压谐波含量在熄弧后急剧减少这一特征检测熄弧时间；基于高频信号的方法容易受TV测量精度的影响。文献[12，13]利用小波变换和自适应神经网络算法实现自适应重合闸，基于人工智能的方法不仅计算量大，而且需要根据不同线路训练大量样本。文献[14]采用自适应累加和算法检测故障相电压连续两次下降和一次上升来判定熄弧时刻，但没有考虑二次电弧阶段故障相电压小幅度持续上升的影响。上述方法均只利用了故障相端电压。

文献[15-17]引入健全相电气信号来确定故障性质和熄弧时刻。文献[15]根据故障相电压相对健全相电压相量和的传输阻抗在熄弧前后呈现的差异，通过检测故障相电压与健全相电压的相角差变化来判断熄弧时间，但二次电弧过零点的瞬间，故障相电压相位计算存在盲区。文献[16]采用瞬时零序功率差动保护，实现动作量自适应的调整，该方法针对同一线路不同故障条件下仿真出二次电弧阶段零序功率值，从而划定熄弧前后零序功率差动范围，但并不能从机理上解释整定保护原则。文献[17]依据零序电压直流偏移来区分瞬时性与永久性故障，其利用零序电压三次谐波分量自适应判断熄弧时刻仍需要高频分量。

当发生单相永久性接地故障，故障相两端断路器跳开后，系统等效于发生同相两侧断线故障，线路侧断相处的各序分量无功功率恒定；当发生单相瞬时性接地故障，在二次电弧阶段，电弧电压的时变特性使得故障相电压不断变化，序分量无功功率也将随着变化。本文基于输电线路电弧模型和电弧电压特性，分析不同性质故障下故障相端电压的变化过程及其对序分量无功功率的影响，揭示线路单相故障后各序分量无功功率的变化规律，提出一种基于序分量无功功率的单相自适应重合闸方案。该方法实现简单，能可靠识别故障性质和快速捕捉熄弧时间，受故障位置的影响小，耐过渡电阻能力强，特别是在重负载线路下其灵敏度反而提高，EMTP仿真验证了其可行性和有效性。

1自适应重合闸实现原理

1.1复功率序分量

高压输电线路一般中性点直接接地，当发生单相接地故障且跳开故障相后，健全相电流和电压近似无变化；而故障相电流为零，故障相电压为电弧电压及耦合电压之和。以A相接地故障为例，令A相电流为参考相量，初始相位角为零，故障前测端电压相位超前于电流φ(cosφ>0.9)。假设故障前三相平衡，其电压、电流分别为

IA=Ia∠0°UA=Va∠φ

(1)

IB=Ia∠-120°UB=Va∠φ-120°

(2)

IC=Ia∠120°UC=Va∠φ+120°

(3)

式中，Ia、Va分别为故障发生前的A相电流和电压的幅值。

故障相断开后，线路侧B、C相电流近似不变，A相电流为0，电流各序分量分别为

(4)

(5)

(6)

式中，a=ej120°；a2=ej240°。由此可以看出断路器跳开后各序电流是一个稳定值。

线路侧的电压各序分量为

(7)

(8)

(9)

根据上述各序电压与电流的值，利用公式S=VI*求出复功率的各序分量

(10)

(11)

(12)

1.2故障相电压对序分量无功功率的影响

当不带并联电抗器的输电线路发生瞬时性单相接地故障且故障相跳开后的二次电弧阶段，电弧电流最大只有几十安培，受健全相电流电磁力以及电弧周围等离子的对流和空气流动的影响，二次电弧长度被不断拉长，电弧电压增大，故障相电压也随着增大[19，20]。在电弧电阻性质的作用下，二次电弧阶段的故障相端电压可用图1所示的等效电路图求出，其近似表达式为

(13)

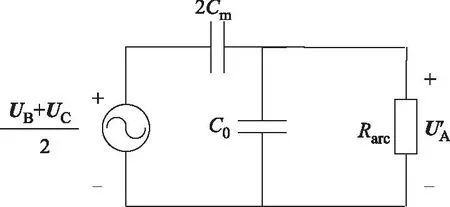
图1　瞬时性故障时故障相端电压Fig.1　Voltage of fault phase under transient fault

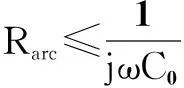
(14)

从式(14)可看出故障相电压相位超前于健全相电压和UB+UC的相位约为90°，即滞后于故障前电压UA相位约90°，其幅值较故障前电压小。将上述关系代入式(10)、式(11)中求得序分量无功功率为

(15)

(16)

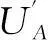
由式(15)、式(16)可推导出正序无功功率与负序无功功率两者增量的比值K为

(17)

式中，ΔQ1、ΔQ2分别为Q1、Q2的增量。

仿真研究发现，受线路参数平衡及故障前负荷平衡程度等因素影响，K值可能在一定范围内偏离-2，即在二次电弧阶段，无功功率正序、负序分量增量的比值基本保持不变，为接近于-2的常数。

1.3熄弧前后序分量无功功率

在二次电弧熄弧瞬间，电弧电阻消失，故障相端电压可用图2所示的等效电路图近似求出，计算故障相电压表达式为

(18)

(19)

(20)

再由式(13)和式(18)得出

(21)

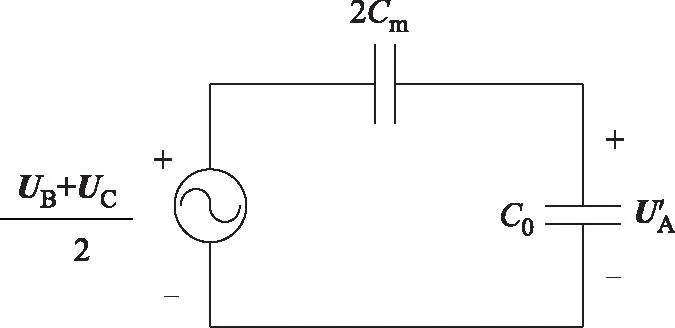
图2　恢复电压阶段故障相端电压Fig.2　Voltage of fault phase on recovery voltage stage

1.4自适应重合闸原理

综上所述，在瞬时性故障下，各序分量无功功率的变化规律如图3所示：在二次电弧阶段，随着故障相电压的逐渐增大，正序无功功率Q1会逐渐下降，而负序无功功率Q2会逐渐上升；在熄弧瞬间，Q1突然增加，而Q2则突然减小，之后两者都恒定在某一值。在永久性故障下，故障相两端跳闸后，由于接地电阻可靠接地，经短暂过渡过程，故障相端电压速衰减至电磁耦合电压，系统进入稳态阶段的定值。正序无功功率Q1和负序无功功率Q2基本恒定，其增量ΔQ1和ΔQ2约为0。基于序分量无功功率的以上特性，提出以下单相自适应实现方案。

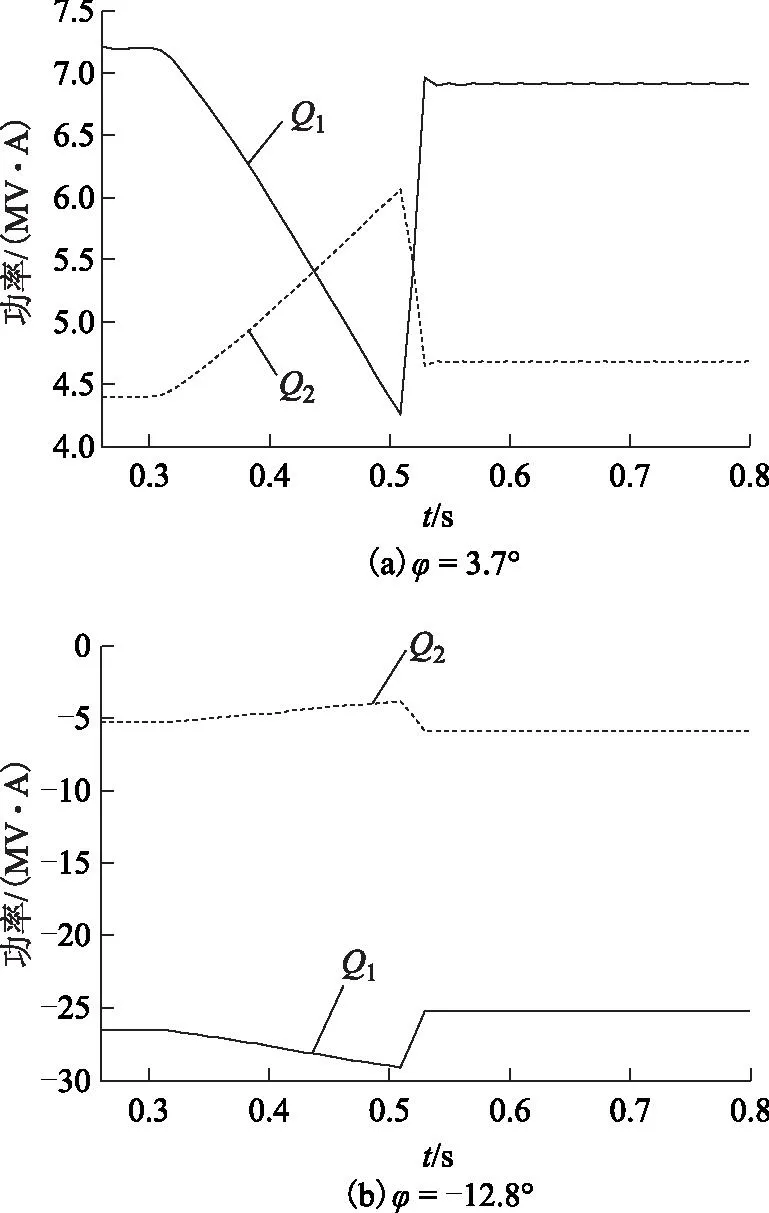
图3　瞬时性故障下无功功率序分量变化Fig.3　Sequence component of reactive power pattern

2自适应重合闸实现方案

2.1故障性质识别判据

选取数据窗长度为1个周波，每次滑动半个周波，使用能滤除衰减直流分量的全波傅氏算法，计算各相基波电压、电流以及正序、负序电压V1、V2和正序、负序电流I1、I2，求出当前正序无功功率、负序无功功率分别为

(22)

(23)

式中，image()为取虚部；符号*表示求共轭。然后计算两者的变化量分别为

ΔQ1(n)=Q1(n)-Q1(0)

(24)

ΔQ2(n)=Q2(n)-Q2(0)

(25)

式中，Q1(0)、Q2(0)分别为正序无功功率、负序无功功率的初次计算值；n=1，2，3，…。

为保证Q1(0)、Q2(0)为二次电弧阶段初始序分量无功功率，取跳闸后第3个周波的采样值开始计算Q1(0)、Q2(0)，这样可以避开断路器跳闸后的剧烈瞬时过程。

对于永久性故障，Q1(n)和Q2(n)基本不变，ΔQ1(n)和ΔQ2(n)均很小。对于瞬时性故障，ΔQ1(n)和ΔQ2(n)取值较大，且其比值近似为-2。

因此当检测到ΔQ1和ΔQ2在连续2个工频周波内均满足

(26)

则判断为瞬时性故障，且已经进入二次电弧阶段。

而若在500 ms内一直不能满足式(26)，则判断为永久性故障，闭锁重合闸。

2.2瞬时性故障熄弧时刻捕捉判据

由前面分析可知，在二次电弧熄弧瞬间，正序无功功率Q1会由逐渐下降突然增加至一恒定值；而负序无功功率Q2会由持续上升突然减小至一恒定值。因此利用两者不同极性的跃变能可靠判断熄弧时间，当检测到Q1和Q2满足式(27)时，判定电弧熄灭，待绝缘恢复后发出重合闸命令。

(27)

2.3自适应重合闸实现步骤

基于以上故障性质识别和熄弧时刻捕捉判据给出自适应重合闸具体实现步骤如下：

1)以2 000 Hz的采样频率对故障线路侧的三相电压和电流进行采样，取跳闸后第3个周波开始的电压、电流信号进行分析。

2)根据式(22)～式(25)求出正序无功功率Q1(n)和负序无功功率Q2(n)以及两者的变化量ΔQ1(n)和ΔQ2(n)，并判断式(26)是否满足。

3)如果在0.5 s内无法满足式(26)，即各序分量无功功率并无明显变化，则判断故障为永久性的，给出重合闸闭锁命令。

4)如果在连续2个工频周波内检测到ΔQ1、ΔQ2满足式(26)，则判定故障为瞬时性，且已进入二次电弧阶段；继续检测当满足式(27)时，判定故障电弧已熄灭并开始计时，延时一定时间(可整定)等待绝缘恢复后发出重合闸命令。

3仿真验证及工程应用

3.1EMTP仿真分析

采用ATP-EMTP对图4所示长度为160 km的不带并联电抗器的500 kV输电线路进行输电线路瞬时性单相接地故障全过程仿真。其中电源功角差系统阻抗参数：Zm1=1+j6.56 Ω，Zm0=2+j9.28 Ω；Zn1=0.48+j8.8 Ω，Zn0=1+j11.68 Ω。输电线路参数：R1=0.016 25 Ω/km，R0=0.157 23 Ω/km；L1=0.905 64 mH/km，L2=1.945 54 mH/km；C1=0.013 26 μF/km，C0=0.010 06 μF/km。电弧模型使用EMTP中TACS模块Type91，初始电弧参数：u0=12 V/cm，t0=1.3 ms，l0=400 cm，r=1.3 mΩ/km[18-20]。

图4　不带并联电抗器输电系统Fig.4　Transmission system without shunt reactors

为了验证上述理论分析的正确性和所提出方案的可行性，在两端电压幅值比为1.05，线路50%处发生故障且接地电阻为50 Ω情况下分别进行了瞬时性和永久性故障仿真实验。图5和图6给出了不同故障性质下式(26)中K1及K2的变化情况。

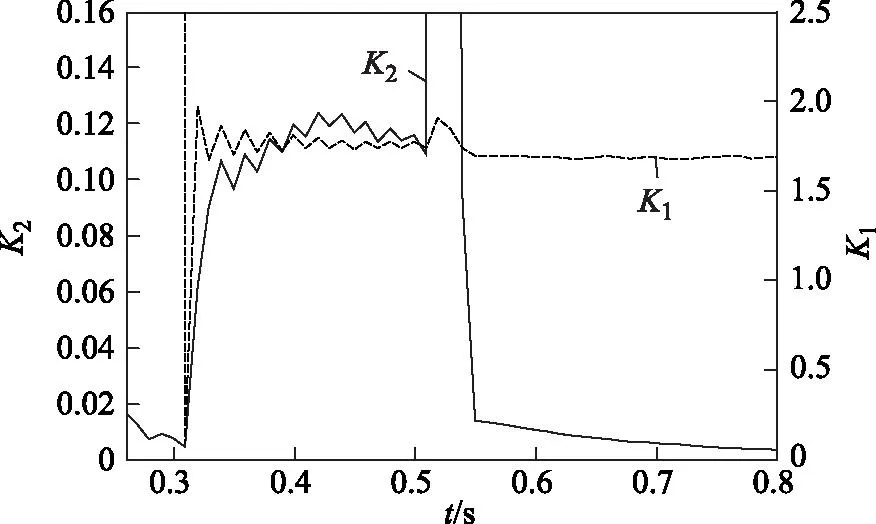
图5　瞬时性故障下K1和K2的变化情况Fig.5　The pattern of K1and K2under transient fault

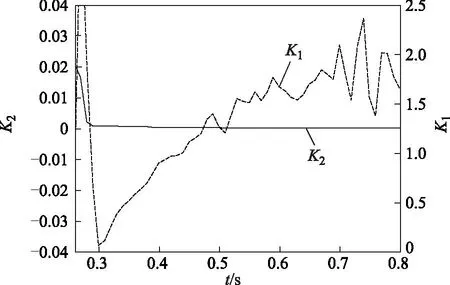
图6　永久性故障下K1和K2的变化情况Fig.6　The pattern of K1and K2under permanent fault

从图5和图6可以看出，在瞬时性故障下，K2在0.10～0.12之间；而永久性故障下，K2一直为接近于零的很小值，因而差异明显。此外，在瞬时性故障下，K1一直恒定于1.7附近，接近于理论分析值2；而永久性故障下，K1值呈现无规律变化。K1值作为辅助判据，使得该故障性质识别方法具有很强的抗噪声能力，也能躲过傅氏算法时间窗内的数据不稳定造成的误判。

本文还针对瞬时性故障在不同电压电流相位差、不同过渡电阻接地、不同故障位置情况下进行了大量的仿真实验。从表1中可以看出，当过渡电阻改变或故障发生点距线路首端距离改变时，K2并无明显变化；尽管K2随电流电压相位差的增大而相应减小，但永久性故障下K2为接近于零的极小值，因此设定门坎值0.01能准确识别故障性质。

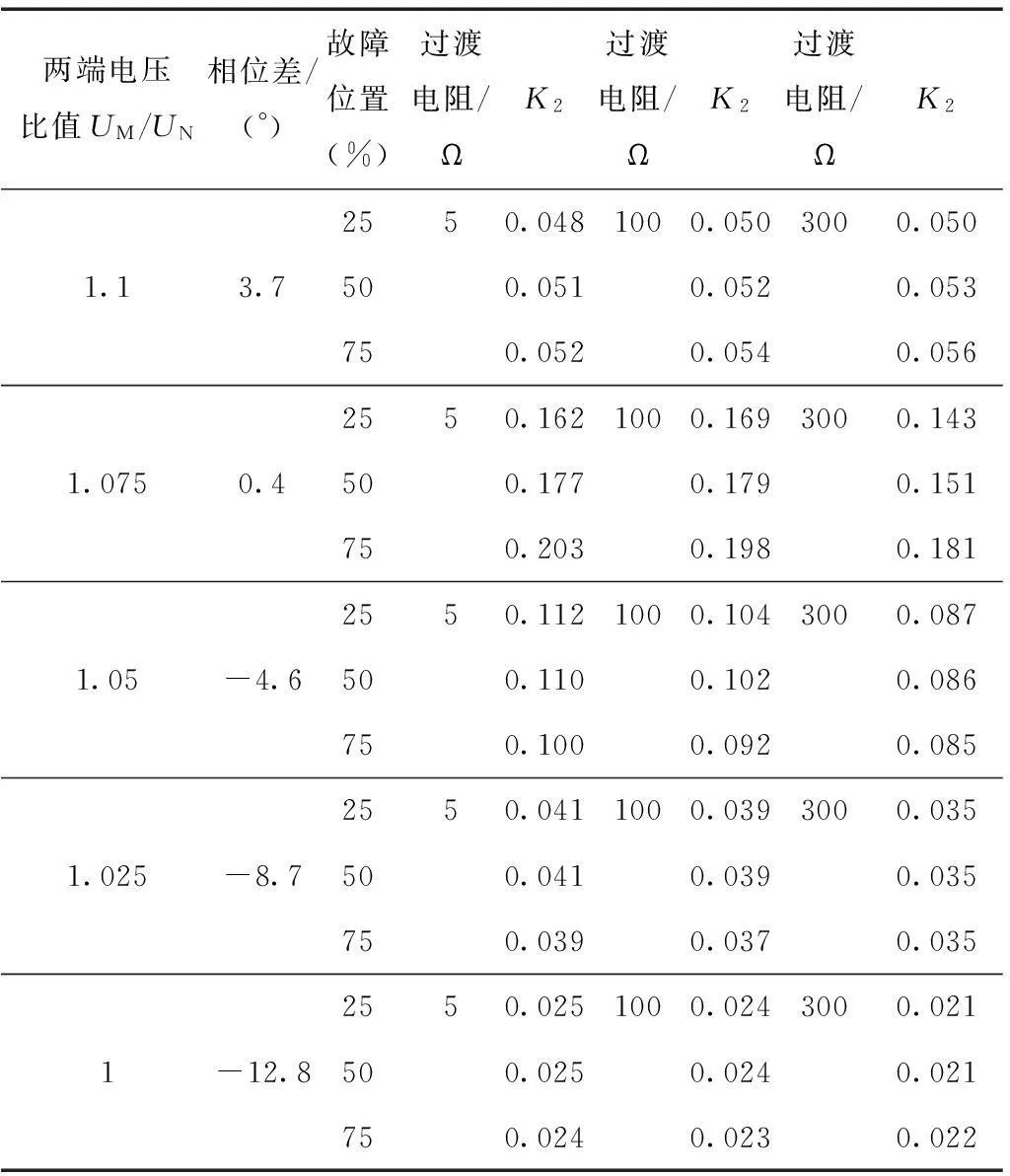
表1　仿真结果示例

表2和表3给出了不同故障位置和接地电阻的情况下，发生瞬时性接地故障时，在二次电弧熄弧瞬间，正序和负序无功功率变化情况。从给出的仿真结果可以看出，在二次电弧熄弧瞬间，各序无功功率的变化值与故障发生位置、接地电阻大小基本无关，其跃变极性与理论分析一致，因而在检测极性的变化的同时，加上一定的跃变阈值就能准确捕捉熄弧时间。

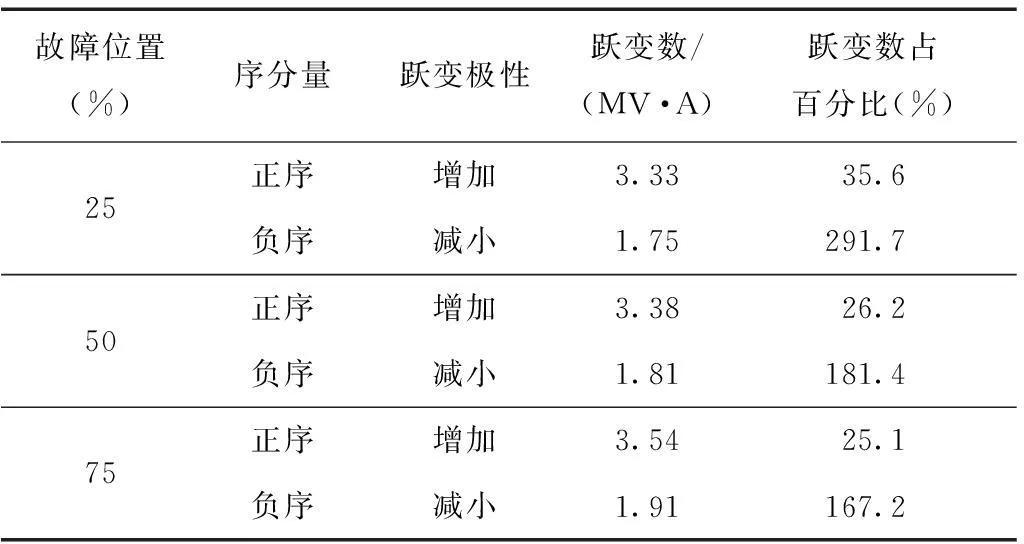
表2　不同故障位置下序分量无功功率跃变情况(UM/UN=1.05，Rf=80 Ω)

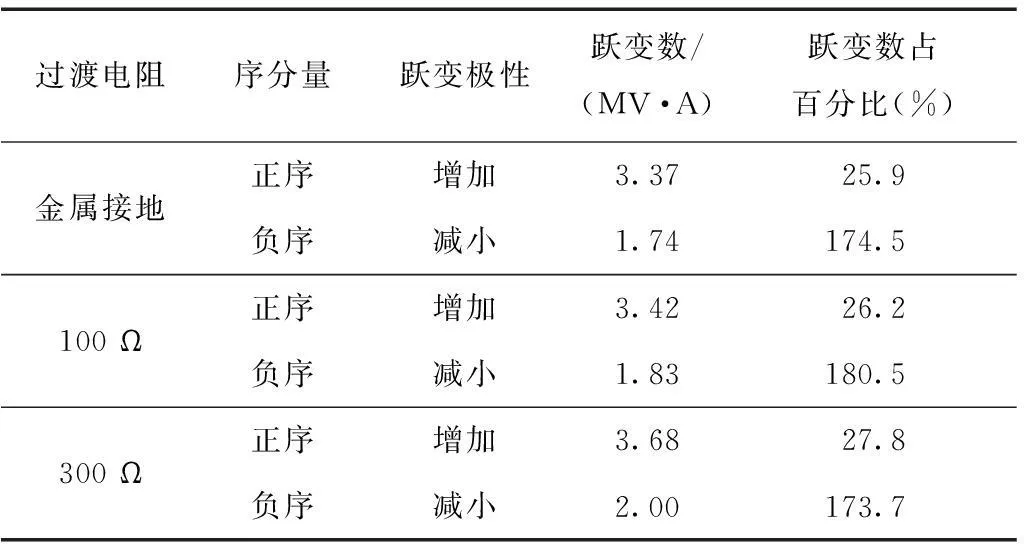
表3　不同接地电阻下序分量无功功率跃变情况(UM/UN=1.05，l=50%)

表4给出了不同功角下，发生瞬时性故障时，在二次电弧熄弧瞬间，正序和负序无功功率变化情况。从表中可以看出，负序无功因其值较小，其跃变数所占百分比总能取到较大值，与表2和表3中一致；正序无功跃变比值随功角的增加而增加。该方法能补充传统电压判据受系统运行方式而灵敏度降低的影响。

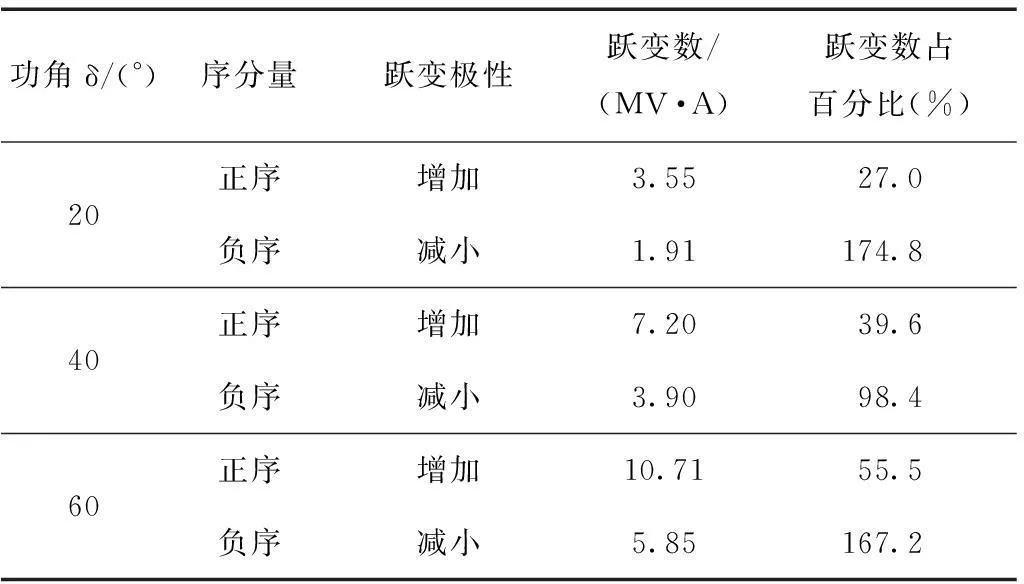
表4　不同功角下序分量无功功率跃变情况(UM/UN=1.05，Rf=100 Ω，l=50%)

表5给出了不同电压、电流相位差下，发生瞬时性故障二次电弧熄弧瞬间，正序和负序无功功率变化情况。从表中可以看出正序和负序无功功率的跃变数与输电线路两端电压比值呈正比，而与跃变数所占百分比呈反比，突变量整定阈值为0.1，完全能满足需要。

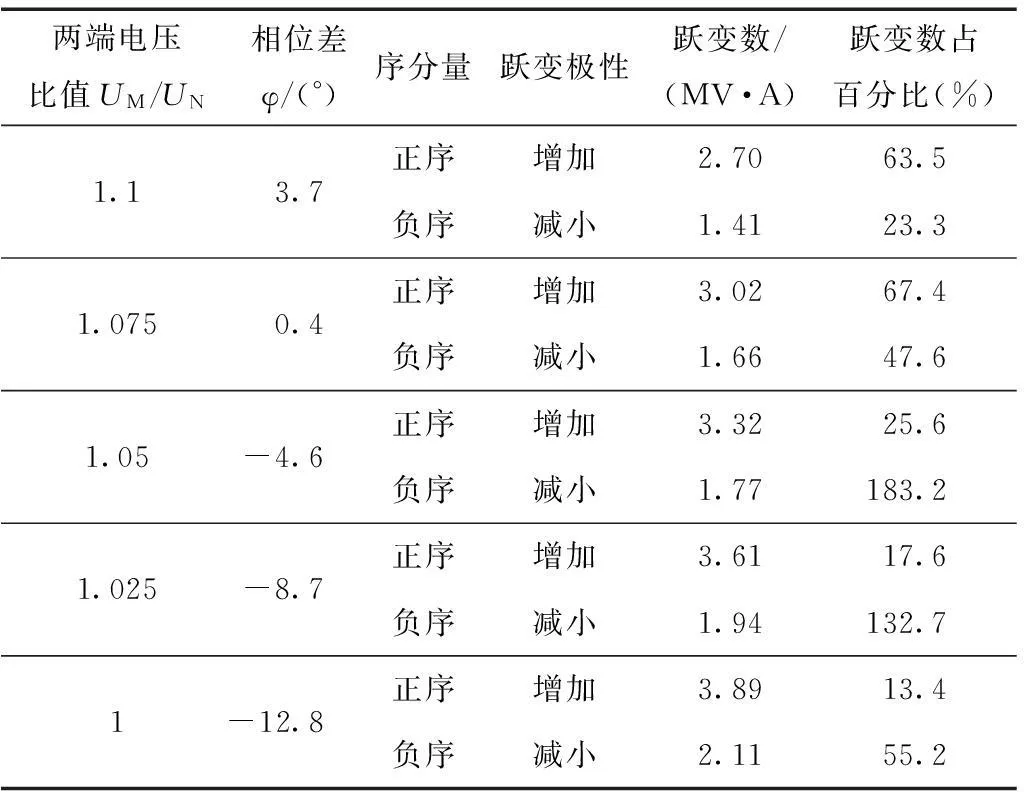
表5　不同相位差下序分量无功功率跃变情况(Rf=50 Ω，l=50%)

3.2工程应用

本文方法只需采用全波傅氏算法计算电压、电流相量及序分量，计算量较小，数据窗较短，对存储容量的要求小；由于只需计算工频参数，对采样频率的要求不高；在一般的微机保护装置硬件配置下，增加软件模块即可将自适应重合闸功能嵌入到现有的线路保护装置中。目前，采用该方法研制的自适应重合闸样机已在某500 kV变电站220 kV线路上挂网试运行。

4结论

探讨了输电线路单相接地故障时正序无功功率与负序无功功率的变化规律，提出了基于序分量无功功率的单相自适应重合闸实现方案。

1)在故障相断路器跳闸后，对于永久性故障，线路经短暂时间过渡到稳态，随后各序分量无功功率基本保持恒定；对于瞬时性故障，在二次电弧尚未熄弧阶段，故障相端电压不断升高，使得序分量无功功率持续变化，正序无功变化量与负序无功变化量的比值为接近于-2的常数；通过检测序分量无功功率的变化率可以准确识别故障性质，且接地电阻只消耗有功功率，对无功功率影响很小，使得该方法耐过渡电阻能力强。

2)在瞬时性故障熄弧瞬间，正序无功功率突然增加，负序无功功率突然减小，均出现较大幅值的跃变，且正序无功跃变比值随着健全相电流增加而增大，使得该方法能在重载线路下灵敏度提高；通过检测各序无功分量的跃变极性和跃变比值，能够准确快速捕捉故障点熄弧时刻，缩短非全相运行时间。

3)该重合闸方案计算量小，数据窗短，对存储容量和采样频率的要求不高，在一般的微机保护装置硬件配置下增加软件模块即可实现，有利于自适应重合闸的推广应用。

参考文献

[1]梁振峰，索南加乐，宋国兵，等.输电线路自适应重合闸研究综述[J].电力系统保护与控制，2013，41(6)：140-147.

Liang Zhenfeng，Suonan Jiale，Song Guobing，et al.Research review of adaptive reclosure in transmission lines[J].Power System Protection and Control，2013，41(6)：140-147.

[2]索南加乐，孙丹丹，付伟，等.带并联电抗器输电线路单相自动重合闸永久故障的识别原理研究[J].中国电机工程学报，2006，26(11)：75-81.

Suonan Jiale，Sun Dandan，Fu Wei，et al.Identification of permanent faults for single-phase auto-reclosure on transmission lines with shunt reactors[J].Proceedings of the CSEE，2006，26(11)：75-81.

[3]李斌，李永丽，盛鹍，等.并联电抗器的超高压输电线单相自适应重合闸研究[J].中国电机工程学报，2004，24(5)：52-56.

Li Bin，Li Yongli，Sheng Kun，et al.The study on single-pole adaptive reclosure of EHV transmission lines with the shunt reactor[J].Proceedings of the CSEE，2004，24(5)：52-56.

[4]刘浩芳，王增平，刘俊岭.带并补的超高压输电线路单相自适应重合闸新判据[J].电力系统自动化，2007，31(24)：62-66.

Liu Haofang，Wang Zengpin，Liu Junling.A new criterion for single-phase adaptive reclosure of shunt reactor compensated EHV transmission lines[J].Automation of Electric Power Systems，2007，31(24)：62-66.

[5]梁振峰，索南加乐，康小宁，等.利用自由振荡频率识别的三相重合闸永久性故障判别[J].中国电机工程学报，2013，33(7)：124-130.

Liang Zhenfeng，Suonan Jiale，Kang Xiaoning，et al.Permanent faults identification using free oscillation frequency for three-phase reclosure on transmission lines with shunt reactors[J].Proceedings of the CSEE，2013，33(7)：124-130.

[6]索南加乐，梁振峰，宋国兵，等.自适应熄弧时刻的单相重合闸的研究[J].电力系统保护与控制，2013，40(5)：37-41.

Suonan Jiale，Liang Zhenfeng，Song Guobing，et al.Study of single-phase reclosure with adaptive secondary arc extinction[J].Power System Protection and Control，2013，40(5)：37-41.

[7]兰华，艾涛，李扬.经验模态分解在单相自适应重合闸中的应用[J].电力系统保护与控制，2010，38(12)：35-39.

Lan Hua，Ai Tao，Li Yang.Application of EMD on single-pole adaptive reclosure of transmission[J].Power System Protection and Control，2010，38(12)：35-39.

[8]郭相国，张保会.自适应自动重合闸现状与发展[J].继电器，2004，32(16)：77-84.

Guo Xiangguo，Zhang Baohui.Present achieve-ments and prospects of adaptive auto-reclosure[J].Relay，2004，32(16)：77-84.

[9]李斌，李永丽，黄强，等.单相自适应重合闸相位判据的研究[J].电力系统自动化，2003，27(22)：41-44.

Li Bin，Li Yongli，Huang Qiang，et al.Study on phase criterion for single-pole adaptive reclosure[J].Automation of Electric Power Systems，2003，27(22)：41-44.

[10]李斌，李永丽，曾治安，等.基于电压谐波信号分析的单相自适应重合闸[J].电网技术，2002，26(10)：53-57.

Li Bin，Li Yongli，Zeng Zhian，et al.Study on single-pole adaptive reclosure based on analysis of voltage harmonic signal[J].Power System Technology，2002，26(10)：53-57.

[11]Radojevic Z M，Shin J R.New digital algorithm for adaptive reclosing based on the calculation of the faulted phase voltage total harmonic distortion factor[J].IEEE Transactions on Power Delivery，2007，22(1)：37-41.

[12]Khorashadi Z H，Li Z.Design of a novel phasor measurement unit-based transmission line auto reclosing scheme[J].IET Generation Transmission &Distribution，2011，5(8)：806-813.

[13]Ozgur K，Hocaoglu M H.An adaline based arcing fault detection algorithm for single-pole autoreclosers[J].Electric Power Systems Research，2011，81(1)：367-376.

[14]Khodadadi M，Noori M R，Shahrtash S，et al.A non communication adaptive single-pole autoreclosure scheme based on the ACUSUM algorithm[J].IEEE Transactions on Power Delivery，2013，28(4)：2526-2533.

[15]Zadeh M R D，Voloh I，Kanabar M，et al.An adaptive HV transmission lines reclosing based on voltage pattern in the complex plane[C]//65th Annual Conference for Protective Relay Engineers，College Station，TX，2012：85-95.

[16]Jamali S，Parham S.New approach to adaptive single-pole auto-reclosing of power transmission lines[J].IET Generation Transmission &Distribution，2010，4(1)：115-122.

[17]Elkalashy N I，Darwish H A，Taalab A M I，et al.An adaptive single pole autoreclosure based on zero sequence power[J].Electric Power Systems Research，2007，77(5)：438-446.

[18]Kizilcay M，Pniok T.Digital simulation of fault arcs in power systems[J].European Transactions on Electrical Power，1991，1(1)：55-59.

[19]Johns A T，Aggarwal R K，Song Y H.Improved technique for modeling fault arcs on faulted EHV transmission systems[J].IET Generation Transmission &Distribution，1994，141(2)：148-154.

[20]Prikler L，Kizilcay M，Ban G，et al.Modeling secondary arc based on identification of arc parameters from staged fault test records[J].International Journal of Electrical Power and Energy Systems，2003，25(8)：581-589.

Single-Phase Adaptive Reclosure Based on Reactive Power of Sequence Components

Luo Xunhua1Huang Chun1Pan Zhimin2Liu Kun2Liang Yongchao2

(1.College of Electrical Engineering &Information TechnologyHunan UniversityChangsha410082China 2.Hunan Electric Examine and Repair CompanyChangsha410004China)

AbstractThis paper proposed an method for single-phase adaptive resclosure based on the reactive power of sequence components for extra high voltage(EHV)transmission lines without shunt reactors.After circuit breaker tripping the fault phase line,for the permanent fault,the voltages and currents of the fault line rapidly get into the steady state,and the reactive power of sequences components becomes almost a constant.However,in the secondary arc stage of transient fault,affected by the arc elongation,the arc voltage and the fault phase voltage increase.Therefore the positive sequence and negative sequence components of the reactive power continue to vary on the contrary way.According to this phenomenon,The rate of variation of positive sequence and negative sequence reactive power components at the faulted line side is used to distinguish fault nature.In the moment of arc extinction,the angle of the faulted phase voltage lags 90°,and then the positive sequence and negative sequence reactive powers have different polarity transitions.According to these phenomena,a new approach based on the reactive power of sequence components is used to identify the fault nature and capture the arc extinction time of the transient fault.The method is simple,hardly influenced by fault resistance and fault distance,and can be utilized in heavy load lines.EMTP simulations have verified its correctness and effectiveness.

Keywords：Transmission line，adaptive reclosing，fault arc，sequence component，reactive power

收稿日期2015-05-07改稿日期2015-10-22

作者简介E-mail：luoxunhuas@163.com(通信作者) E-mail：yellowpure@hotmail.com

中图分类号：TM77

国家高技术研究发展(863)计划(2012AA050215)和国家电网公司研究开发项目(5216A313500N)资助。

罗勋华男，1989年生，博士研究生，研究方向为电力系统继电保护、电气信号处理。

黄纯男，1966年生，教授，博士生导师，研究方向为电力系统保护与控制、电能质量分析与控制、信号处理。