有限字长对滑动窗DFT稳定性的影响研究

刘华吾　胡海兵　邢　岩

(南京航空航天大学自动化学院 江苏省新能源发电与电能变换重点实验室　南京　210016)

有限字长对滑动窗DFT稳定性的影响研究

刘华吾胡海兵邢岩

(南京航空航天大学自动化学院 江苏省新能源发电与电能变换重点实验室南京210016)

摘要滑动窗离散傅里叶变换(DFT)具体数字实现过程中，有限字长效应引入的误差会被累积和放大，易造成系统发散和不稳定。针对该问题和现象，应用随机信号的统计特性，详细分析了信号量化噪声、旋转因子量化误差及数学运算舍入误差对滑动窗DFT稳定性的影响，并指出舍入误差所引入的直流分量是导致系统不稳定的根本原因。仿真和实验均验证了理论分析的正确性。为了解决此不稳定问题，提出两种通过交换运算次序来消除误差累积和放大的解决方案，实验和仿真结果验证了这两种方法的有效性。

关键词：有限字长效应滑动窗DFT稳定性舍入误差

0引言

离散傅里叶变换(Discrete Fourier Transform，DFT)是数字信号处理中的重要工具[1-4]。传统的傅里叶变换或快速傅里叶变换(FFT)运算量大，很难满足实时性要求较高的应用场合[5，6]。近年来提出的迭代形式DFT即滑动窗DFT[7，8]，由于其运算量小及实时性好等优点，得到了广泛关注，被应用于实时频谱分析、继电保护和电力系统谐波提取等领域[9-14]。

实际数字系统中，有限字长效应引入的信号抽样误差、滤波器系数量化误差、计算舍入误差等会给系统的精度和稳定性带来不良影响。滑动窗DFT的极点分布在离散域的单位圆上，是一个临界稳定系统，文献[7，14]指出，旋转因子系数的量化误差可能会将系统极点移出单位圆，致使系统不稳定，但文中没有考虑其他误差对系统稳定性的影响。文献[15]指出，滑动窗DFT大量乘法的舍入误差会在系统中无衰减传播和累积，文中应用随机信号的方差特征分析误差的放大效应，没有考虑误差正负的相互抵消因素。文献[16]详细描述了浮点数实现滑动窗DFT的不稳定现象，但未给出清晰的理论解释。

针对上述稳定性问题，现有文献提出了许多解决措施。引入衰减因子法[7，17]将滑动窗DFT的极点强行移至单位圆内，对误差的传播形成衰减和阻尼，这种方法简单可靠，但会引入额外运算量且易导致输出失真。基于Goertzel算法的改进DFT[15]和并行DFT[16，18，19]迭代形式的DFT并行运算，在每个变换周期结束后，用非迭代DFT的输出更新迭代DFT的数据，避免误差的累积。该方法输出结果准确可靠，但实现结构复杂、运算量大。优化DFT法[16，20]通过优化算法运算顺序避免误差的累积和放大，具有结构简单和运算量少的优点，但需要占用2倍的存储空间[21，22]，不适合需要同时提取多个频谱的应用场合。

本文首先给出了滑动窗DFT的数学表达式，指出具体数字实现过程中有限字长效应引入的误差，提出了一种稳定性分析模型，全面详细分析了各种误差对系统稳定性的影响，得出舍入误差引入的直流分量是导致不稳定现象的原因的结论，并进行了详细的仿真和实验对比，验证了理论分析的正确性。最后，针对此稳定性问题，基于优化算法运算顺序的思想，提出了两种简洁有效的解决措施，并进行了仿真和实验验证。

1滑动窗DFT

用采样频率N/T0采样输入信号x(t)，生成离散序列{x(n)}，从中选取N点作为样本。设第n-1次样本序列为{x(n-N)，x(n-N+1)，…，x(n-1)}，其m次谐波设为Xm(n-1)。一个采样周期之后，第n次的样本序列在上次的样本中移除x(n-N)，加入x(n)，生成{x(n-N+1)，x(n-N+2)，…，x(n)}，该新样本的m次谐波为Xm(n)。则Xm(n-1)和Xm(n)有以下关系[23]

Xm(n)=Xm(n-1)+[x(n)-x(n-N)]ejω0(n-1)m

(1)

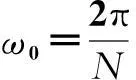
(2)

θm(n)=∠Xm(n)

(3)

式(1)～式(3)即是滑动窗DFT的计算公式，以提取基波频谱为例，实现框图如图1所示。

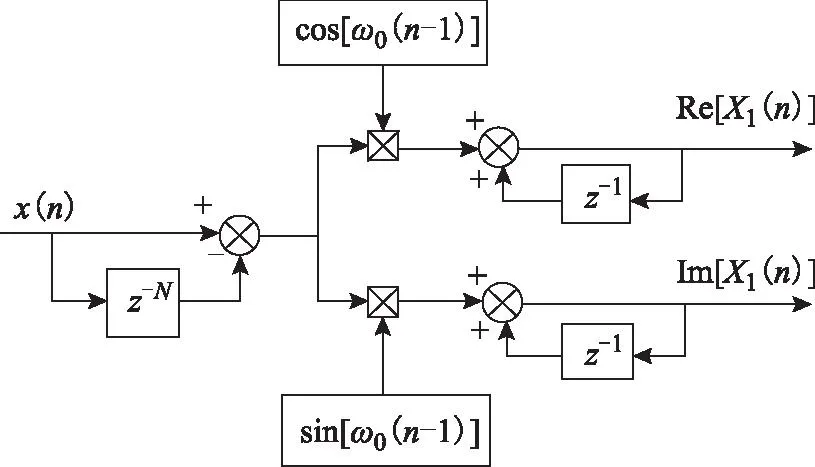
图1　滑动窗DFT实现框图Fig.1　Block diagram of recursive DFT

理论上，若输入是周期信号且频率等于1/T0(本文T0=1/50 s)，则x(n)-x(n-N)=0；X1(n)保持上个采样周期的值不变。当输入信号频率波动Δf而DFT采样频率保持不变时，x(n)-x(n-N)≠0，DFT输出X1(n)也会有相应的脉动，但系统稳定，不会随时间推进而发散[24]。

然而具体数字实现过程中，有限字长的效应会引入各种误差，包括模拟信号抽样产生的量化噪声、旋转因子的量化误差、数学运算的舍入误差[25]。这些误差在离散系统中传递，经滑动窗DFT无限次迭代后，易被累积和放大，最终导致系统输出发散和不稳定。

2有限字长对滑动窗DFT的稳定性影响

为分析滑动窗DFT的稳定性问题，可将图1的实现框图简化为图2所示的分析模型。

图2　滑动窗DFT的简化模型Fig.2　Simplified analysis model of the sliding DFT

图2中M表示运算

vq(n)=[x(n)-x(n-N)]ejω0(n-1)

(4)

式(4)对应的离散域传递函数是一个有限脉冲响应(FIR)系统，无输出到输入的反馈，不会累积和放大误差，也不会导致系统输出不稳定。而图2中的数据累加部分包含输出到输入的反馈，本质是一个积分器，对直流分量有无穷大增益。这意味着，如果输入vq(n)含有直流分量，则会被无限累积和放大而导致输出发散。可见，滑动窗DFT的迭代形式是其实际数字过程中存在稳定性问题的前提。相反的，如果系统输出不稳定，必然是由于vq(n)含有直流分量。因而下文将围绕是否会在vq(n)引入直流分量，对有限字长效应引入的各种误差展开详细分析。

滑动窗DFT可采用定点数或浮点数实现，稳定性分析方法类似，本文针对定点数场合。由图1可知，滑动窗DFT提取频谱的实部和虚部对称，选取实部的运算过程作为研究对象，考虑数字实现过程中所有可能的误差，可得到如图3所示的稳定性分析模型。模型被划分为信号量化、梳状滤波器、旋转因子相乘、数据舍入和累加等五部分，其中es(n)表示信号抽样的量化噪声，eR(n)表示旋转因子的量化误差，ev(n)表示乘法运算的舍入误差。

图3　滑动窗DFT的稳定性分析模型Fig.3　Analysis model of the practically implemented sliding DFT

2.1信号量化

滑动窗DFT的输入vs(t)经采样量化成离散序列vt(n)，实际的采样量化过程可等效成理想的抽样叠加量化噪声[25]

vt(n)=vs(n)+es(n)

(5)

式中，vs(n)为理想抽样结果；es(n)为量化噪声，是一个平稳随机序列[25，26]，其统计均值μes=μ(和时间无关的常数)。

量化噪声es(n)经过梳状滤波器、旋转因子相乘和数据舍入等模块最终传递到vq(n)，它对系统稳定性的影响在2.5节论述。

2.2梳状滤波器

梳状滤波器离散域传递函数为

H1(z)=1-z-N

(6)

其频率响应为

H1(ejω)=1-e-jNω

(7)

易知，当ω=kω0=2kπ/N(k=0，±1，…，±N-1)时，H1(ejω)=0，这表明梳状滤波器完全滤除直流分量和频率为ω0及其整数倍谐波。

信号量化模块的输出vt(n)，经梳状滤波器后为vr(n)

vr(n)=vt(n)h1(n)=[vs(n)+es(n)]h1(n)

=vs(n)h1(n)+es(n)h1(n)

=vrs(n)+vrv(n)

(8)式中，h1(n)=δ(n)-δ(n-N)，表示H1(z)的单位序列响应；vrs(n)是输入确定信号vs(n)经梳状滤波器的响应输出，由梳状滤波器的特性知，vrs(n)不含有直流分量和频率为ω0及其整数倍谐波分量；vrv(n)是一个随机信号，由量化噪声es(n)经梳状滤波器的输出，其统计平均值[25]

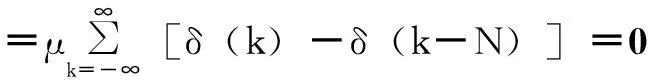
(9)

式(9)表明随机信号vrv(n)的统计均值为零，和量化噪声es(n)的统计数字特征μ无关。

2.3旋转因子相乘

定点数表示旋转因子时，需要先定标(乘以2Q，然后取整)，定标取整引入的量化误差记为eR(n)，如图3所示。eR(n)是一个平稳的随机序列[25，26]，统计均值E[eR(k)]=ε(常数)。

vr(n)经旋转因子相乘后的vp(n)为

vp(n)=vr(n){2Qcos[ω0(n-1)]+2QeR(n)]}

(10)

2.4数据舍入和累加

旋转因子相乘后的舍入误差记为ev(n)。由图3可知，最终累加部分的输入vq(n)为

(11)

结合式(8)和式(10)，将式(11)展开得

vq(n)=y1(n)+y2(n)+y3(n)+y4(n)+y5(n)

(12)

式中

y1(n)=vrs(n)cos[ω0(n-1)]

y2(n)=vrs(n)eR(n)

y3(n)=vrv(n)cos[ω0(n-1)]

y4(n)=vrv(n)eR(n)

y5(n)=ev(n)

(13)

式中，y1(n)是确定信号；y2(n)～y5(n)是随机信号，表示旋转因子量化误差、抽样量化噪声和数字运算舍入误差等对滑动窗DFT的稳定性影响。

2.5稳定性分析

y1(n)是确定信号，2.2节指出vrs(n)不含频率为ω0分量，则乘积vrs(n)cos[ω0(n-1)]必然没有直流分量(详细数学证明见附录A)，不影响系统稳定性。

随机信号y2(n)～y5(n)的直流分量通常用统计均值表示[25]。

y2(n)的统计均值为

E[y2(n)]=E[vrs(n)eR(n)]=vrs(n)E[eR(n)]

=εvrs(n)

(14)

由于vrs(n)是无直流分量的确定信号，因而y2(n)不会影响系统的稳定性(详细分析见附录B)。

y3(n)的统计均值为

E[y3(n)]=E{vrv(n)cos[ω0(n-1)]}

=cos[ω0(n-1)]E[vrv(n)]

=μrvcos[ω0(n-1)]

(15)

由式(9)知μrv=0，因而E[y3(n)]=0，从而y3(n)无直流分量，不影响系统的稳定性。

y4(n)的统计均值为

E[y4(n)]=E[vrv(n)eR(n)]

(16)

考虑到随机信号vrv(n)和eR(n)不相关，有

E[y4(n)]=E[vrv(n)]E[eR(n)]=μrvE[eR(n)]=0

(17)

可见，y4(n)同样无直流分量，不影响系统的稳定性。

y5(n)是乘法运算的舍入误差，其统计均值和舍入方式有关。直接截尾和四舍五入是两种最常用的舍入方式，直接截尾法将尾数直接舍去，实现最简单。四舍五入法根据尾数的最高位数字来决定是否进位，实现相对复杂。

y5(n)的实际统计均值与抽样样本大小、随机实验次数以及数值的波动范围等有关。这和y3(n)、y4(n)不同，由式(5)～式(17)可知，y3(n)、y4(n)的统计均值直接由vrv(n)的统计特征决定；梳状滤波器完全滤除直流分量的特性保证了vrv(n)的统计均值μrv=0(式(9))而和随机过程无关。

采用直接截尾法时，虽然无法准确求取其统计均值，但每次舍入时均将尾数直接舍去，y5(n)<0恒成立，从而

E[y5(n)]<0

(18)

这说明直接截尾法的舍入误差会引入负的直流分量，必然导致系统不稳定。

采用四舍五入法时，每次舍入的尾数可正可负，当抽样样本无限大、随机实验次数无限多、乘法运算的数值均匀分布时，y5(n)的统计均值趋于零。这些条件在实际系统中显然很难保证。相反的，很可能在一段时间内E[y5(n)]>0，而在另一段时间内E[y5(n)]<0。y5(n)统计均值的这种正负波动将致使滑动窗DFT输出频谱的实虚部往+∞或-∞方向发散，引起误差累积和放大，易导致输出不可靠。

总结上述分析，得到以下结论：

1)输入信号波动、A-D量化噪声和旋转因子系数量化误差不影响系统稳定性。

2)直接截尾法会引入负直流偏置，必然导致系统输出的频谱实虚部往-∞方向发散。

3)四舍五入法引入的误差，在实际系统中很难保证其统计均值为零，易导致系统输出不可靠。

2.6稳定性问题的仿真和实验验证

为验证上文分析的正确性，搭建了仿真模型和实验平台，对滑动窗DFT进行详细仿真和实验。

图4为Matlab/Simulink中的仿真模型。量化系数取214/5，输入信号叠加白噪声，模拟实际采样电路和A-D量化引入的噪声，量化模块的步长取5/2-14。计算过程采用Q14定标，旋转因子定标值采用直接尾数截断法。计算模块尾数的舍入，为对比研究，分别采用四舍五入或直接截尾法。

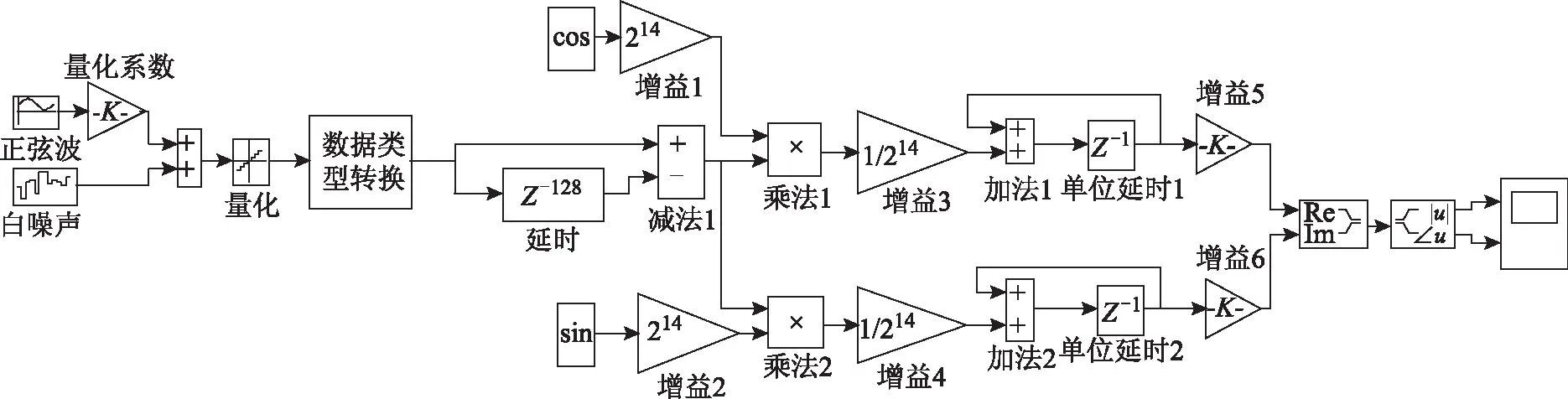
图4　滑动窗DFT Matlab仿真模型Fig.4　Matlab simulation model of the sliding DFT

搭建了实验平台，平台采用现场可编程门阵列(FPGA，EP4CE15F17C8)作为控制器，任意函数发生器(DG4072)作为信号输入源。输入信号通过14bit-A-D(ADS7945)输入至FPGA，A-D的基准由芯片(AD586)生成。FPGA计算结果经16bit-D-A(DAC8501)转换成模拟量，输出至示波器。实验中滑动窗DFT实现架构和图4仿真模型一致。

仿真和实验中，用滑动窗DFT提取输入信号的基波频谱，DFT变换点数N为128，采样频率为6 400 Hz。

1)实例一：频率49.5 Hz正弦波输入，旋转因子乘法运算尾数舍入采用直接截尾法。

仿真中，输入信号为频率49.5 Hz的正弦波

vs(t)=sin(49.5·2πt)

(19)

实验中，由信号发生器生成幅值1 V、频率49.5 Hz的正弦波，经A-D量化后输入至滑动窗DFT。

图5为系统运行初始的仿真和实验结果，其中A和θ分别表示DFT输出的幅值和相角。

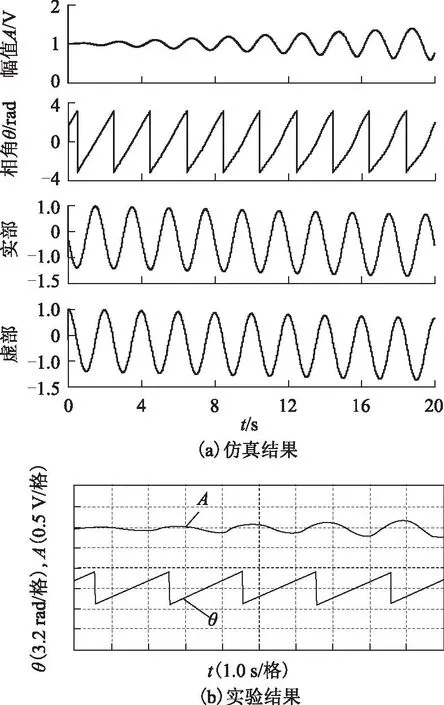
图5　滑动窗DFT的仿真和实验结果(实例一)Fig.5　Simulation and experimental results of the recursive DFT under conditions of the first case

从图5中可明显看出，DFT输出的幅值迅速发散，相角也随之明显畸变。频谱的实虚部含有幅值保持不变的交流分量和往-∞发散的直流分量。交流分量由输入信号为0.5 Hz的频率偏差引起，不影响系统稳定性。直流分量由舍入误差引入，经DFT输出累积部分迭代后，迅速累积和放大，致使系统发散。

2)实例二：频率49.5 Hz正弦波输入，旋转因子乘法运算尾数舍入采用四舍五入法。

在该实例中，滑动窗DFT的输入和实例一保持一致，仅将舍入方式改成四舍五入法。

仿真模型和实验平台运行10 s、1 h和20 h结果分别如图6a～图6f所示。可以看出，仿真和实验刚开始时，DFT输出的幅值和相角是准确可靠的，但随着时间的推进，幅值A上叠加的低频脉动被逐渐放大，只是发散的速度非常缓慢。实验20 h后，低频脉动的幅值约0.1 V，比仿真的结果大，这是由于实验和仿真中A-D采样量化噪声的不一致造成的。此外，受四舍五入引入的舍去误差统计均值的正负波动影响，该低频脉动不是一直被放大，存在被缩小的时候，因文章篇幅限制，此处略去相应的实验和仿真波形。总而言之，即便采用较为复杂的四舍五入舍入方式，滑动窗DFT输出依然不可靠。

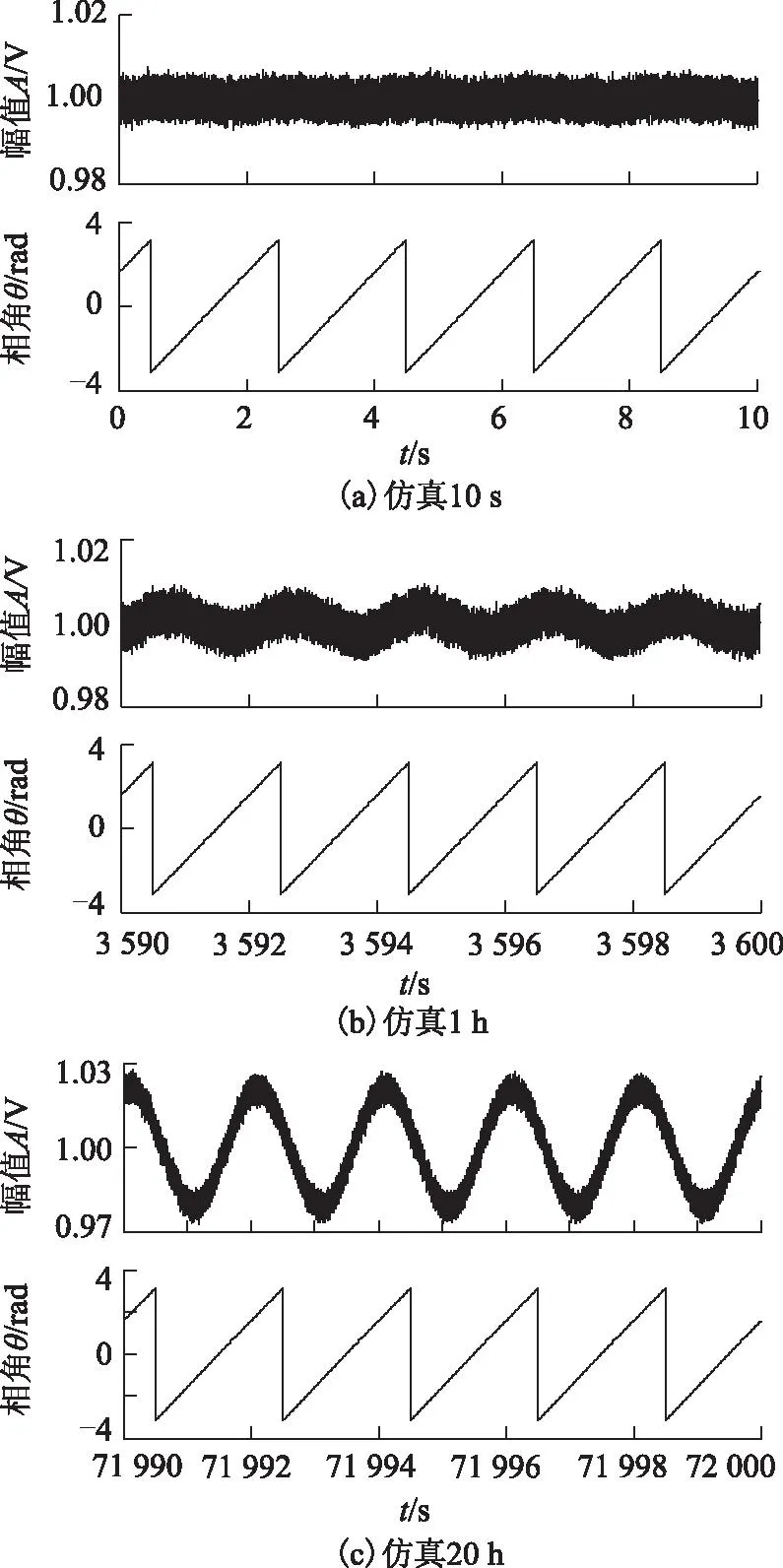
图6　滑动窗DFT的仿真和实验结果(实例二)Fig.6　Simulation and experimental results of the recursive DFT under conditions of the second case

3解决方法

3.1改进DFT法

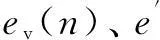
从图7可看出，改进DFT法的实现简洁方便，不会引入额外的存储空间和运算量，仅会使数据累加部分的加法运算位宽扩大Q位。

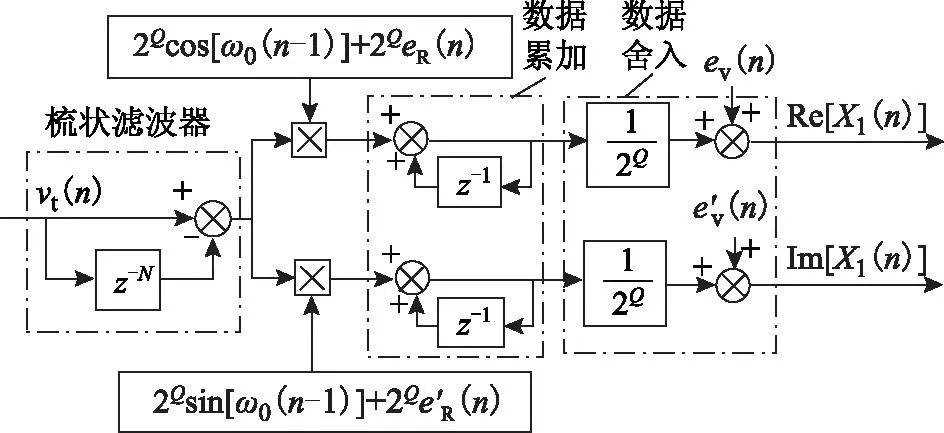
图7　改进DFT法Fig.7　Modified DFT technique

3.2改进并行DFT法

图2分析指出，滑动窗DFT稳定的前提是数据累加部分的输入不含直流分量。3.1节提出的改进DFT法的核心是通过交换运算次序将“直流分量的产生源——数据舍入”移至DFT最终输出，避免其进入数据累加部分。此方法适合定点数运算，但在浮点数计算场合，由于无法直接和方便地控制数据舍入，其不再适用。在这种情况下，本文采用另外一种思路：滤除直流分量。

为滤除直流分量，保证系统稳定性，最直接的方法是在数据累加部分之前插入额外的低阻滤波器，但这会增加运算量且可能影响DFT提取频谱的精度。而从对图3的分析可知，滑动窗DFT中已存在可以完全滤除直流分量的梳状滤波器，因而无须再引入额外滤波器，仅须调整运算次序，将其移至数据累加部分之前，如图8所示。

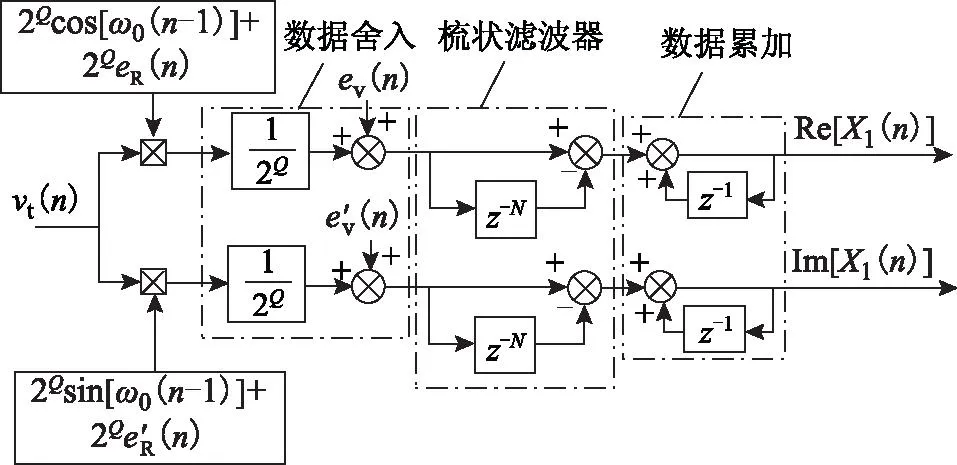
图8　优化并行DFT法Fig.8　Optimized parallel DFT technique

优化并行DFT法中，梳状滤波器紧挨数据累加部分，相比于滑动窗DFT的传统实现方式(见图1或图3)，其不仅可剔除输入信号、A-D采样量化等引入的直流偏置，还可以滤除数据舍入引入的直流分量，从而无直流偏置进入数据累加部分，保证系统稳定性。

优化并行DFT法可靠有效，其仅将梳状滤波器移至数据累加之前，相比于改进DFT法，无须对数据舍入部分作特别处理，因此适用于定点数和浮点数运算场合。然而，这种方法占用2N存储空间，且当需要同时提取多次频谱时，占用的存储空间将会成倍数增加，因而需要进一步优化该方法。

图8所示优化并行DFT法对应的数学表达式为

X1(n)=X1(n-1)+vt(n)ejω0(n-1)-vt(n-N)ejω0(n-1-N)

(20)

考虑到

ejω0(n-1-N)=ejω0(n-1)-2π=ejω0(n-1)

(21)

因而，式(20)可简化为

X1(n)=X1(n-1)+vt(n)ejω0(n-1)-vt(n-N)ejω0(n-1)

(22)

式(22)对应的具体实现框图如图9所示。改进并行DFT法和图8所示的优化并行DFT法等价，只是前者利用旋转因子的周期对称性质，进一步优化了具体实现过程。此外，该算法虽然额外增加了两次乘法和一次减法，但仅占用N存储空间，且存储空间不会随提取频谱次数的增加而增加。因而该方法特别适用于存储资源有限或需要同时提取多个频谱的应用场合。

图9　改进并行DFT法Fig.9　Modified parallel DFT technique

3.3实验验证

为验证本文提出的两种算法的可行性，进行了实验研究。考虑到图7所示的改进DFT法仅适用于定点数计算，而图9的改进并行DFT法适用于定点数和浮点数，因此本文验证滑动窗DFT的3种具体实现方式如下：

1)采用定点数运算和直接截尾的舍入方式，实现改进DFT法。

2)采用定点数运算和直接截尾的舍入方式，实现改进并行DFT法。

3)运用FPGA中的自带浮点数运算IP核，采用单精度(single)型计算方式，实现改进并行DFT法。

实验研究主要分为两部分：第一部分以信号发生器作为信号输入源，第二部分将本文提出的算法应用于有源滤波器(APF)中。

1)以信号发生器作为信号输入源

该部分的实验平台和2.6节的一致，如图10所示，以Altera公司的FPGA(EP4CE15F17C8)作为核心控制单元，任意函数发生器(DG4072)作为信号输入源。

图10　基于信号发生器的实验平台Fig.10　Experimental setup based on signal generator

信号发生器输出1 V/49.5 Hz正弦波，在FPGA中分别采用上述滑动窗DFT的3种实现方式，提取50 Hz基波，验证算法的可靠性。平台运行约20 h后，3种算法的实验波形一致，如图11所示，其中vs为输入信号，vf为DFT提取的基波时域信号，A和θ分别为DFT输出的幅值和相角。从图中可看出，输入信号频率偏差、舍入和量化误差等因素均未导致DFT输出发散，系统稳定可靠。

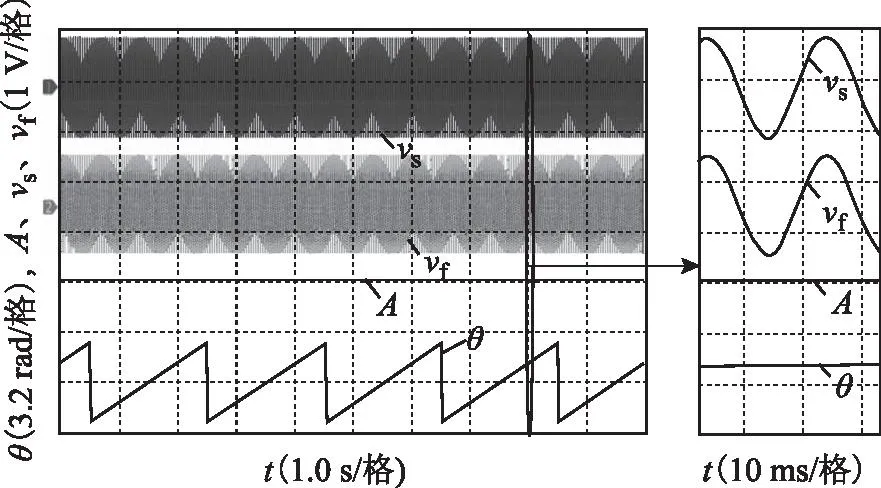
图11　滑动窗DFT运行20 h的实验结果Fig.11　20 h-post simulation and experimental results of the recursive DFT

2)并联型选择性APF实验研究

该部分实验将滑动窗DFT应用到实验室20 A单相并联型选择性APF的样机平台上，如图12所示。实验平台采用FPGA作为核心控制器，主电路开关器件为F4-50R06W1E3。FPGA控制器利用滑动窗DFT提取非线性负载中的各次谐波，然后控制APF输出相应的电流以抵消电网中的谐波，提高电能质量。APF电流的控制采用比例谐振调节器(PR)，以实现无静差谐波基准跟踪。

图12　APF实验平台Fig.12　APF experimental setup

将上述滑动窗DFT的3种实现方式(定点数运算的改进DFT法，定点数和浮点数运算的改进并行DFT法)分别在实验平台上验证。3种实现方式下APF输出波形均一致，如图13所示。图中，iL为非线性负载的谐波波形，iC为APF输出电流波形，iS为电网电流波形。图13a中，APF仅补偿3次谐波的波形，电网电流中3次谐波成分从补偿前的5.32 A降到0.05 A；图13b为APF补偿3～21次谐波的波形，电网电流THD从补偿前的55.96%降到6.03%。图13说明了本文提出的方法能够准确提取谐波，验证了算法的可行性。

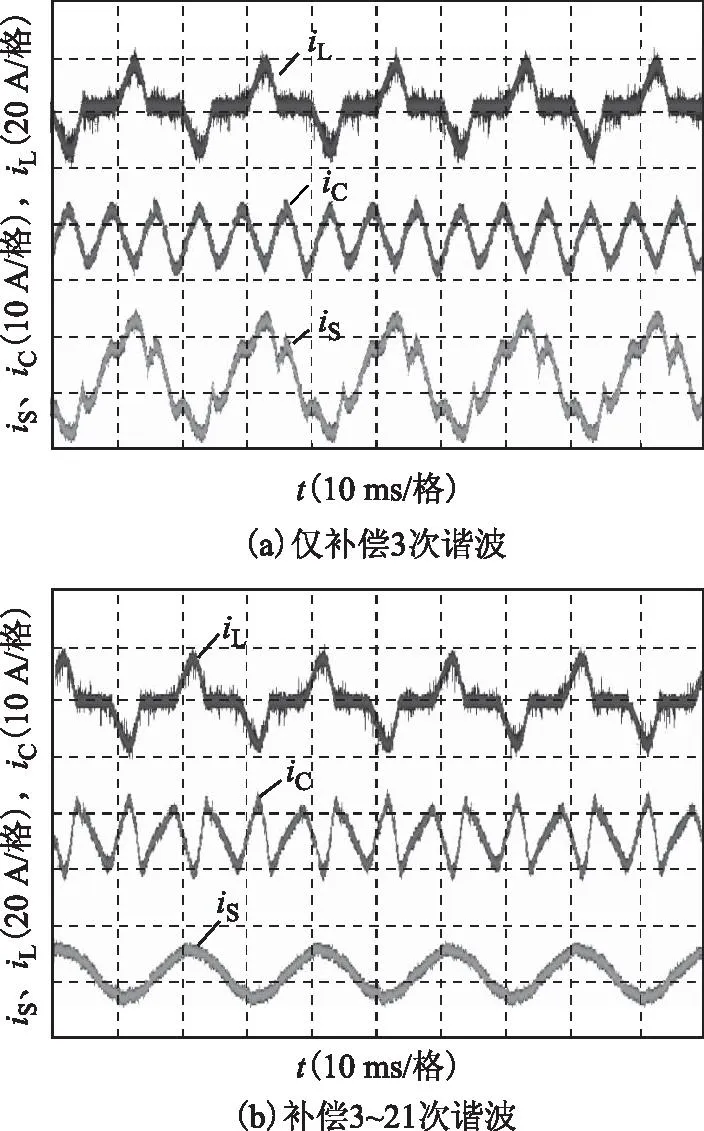
图13　APF实验结果Fig.13　APF experimental results

为进一步验证算法的稳定性，以同时补偿3～21次谐波为例，将滑动窗DFT的3种实现方式下的APF分别进行了约10 h的拷机实验，拷机过程中APF能够稳定运行，系统最终输出和图13所示保持一致，说明了算法的可靠性。

以上实验结果表明，采用本文提出的改进DFT法和改进并行DFT法，能够准确提取谐波频谱，有效避免有限字长效应引起的稳定性问题，保证系统可靠输出，从而验证了算法的可行性和有效性。

4结论

深入分析了有限字长效应对滑动窗DFT稳定性的影响。理论分析和仿真实验表明，乘法运算的舍入误差会在系统数据累加部分引入直流分量，导致输出发散，而输入信号量化噪声和旋转因子系数量化误差等均不会影响系统稳定性。

针对滑动窗DFT的不稳定问题，基于优化运算顺序的思想，提出了改进DFT法和改进并行DFT法，前者占用资源最少，适用于定点数运算，后者适用于浮点或定点数运算。此外，这两种方法均不会占用额外存储空间，适用于需要同时提取多个频谱的应用场合。

附录

附录 A：证明y1(n)=vrs(n)cos[ω0(n-1)]不含直流分量。

由三角函数性质可知

y1(n)=vrs(n)cos[ω0(n-1)]

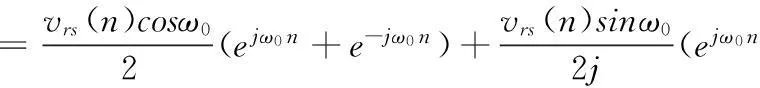
(A1)

设vrs(n)和y1(n)对应的傅里叶变换分别为Vrs(jω)和Y1(jω)，则由式(A1)知

(A2)

从而y1(n)的直流分量

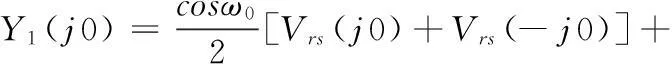
(A3)

本文中2.2节已经指出，vrs(n)不含频率为ω0及其整数倍谐波分量，即Vrs(j0)=Vrs(-j0)=0，从而Y1(j0)=0，表明y1(n)无直流分量。

附录 B：证明随机信号y2(n)=vrs(n)eR(n)不影响滑动窗DFT的稳定性。

设y2(n)经滑动窗DFT的累加部分后输出为R2(n)，则

(B1)

本文中第2节指出，输出累加部分仅对直流分量增益无穷大，因而可通过分析R2(n)的直流分量来评估y2(n)对系统稳定性的影响。

随机信号y2(n)的统计均值

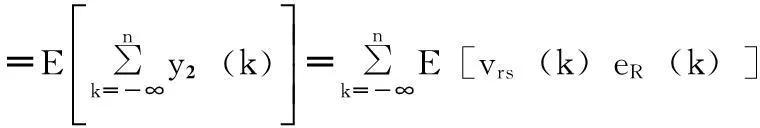
(B2)

式中，ε是一个常数，表示eR(n)的统计均值。考虑到vrs(n)是一个无直流分量的确定信号，∑vrs(k)和E[R2(n)]必然是一个有界值，不会随时间推进(n变大)而发散，故而y2(n)不影响系统稳定性。

参考文献

[1]王尧，李奎，任伯飞，等.基于全相位傅里叶变换的磁调制交直流漏电电流检测方法[J].电工技术学报，2015，30(18)：254-260.

Wang Yao，Li Kui，Ren Bofei，et al.Study of fluxgate current detecting method for AC-DC earth leakage current based on apFFT[J].Transactions of China Electrotechnical Society，2015，30(18)：254-260.

[2]孙晓云，同向前，高鑫.柔性直流输电系统中IGBT阀的故障诊断方法[J].电工技术学报，2014，29(8)：235-241.

Sun Xiaoyun，Tong Xiangqian，Gao Xin，et al.Research on the fault diagnosis of IGBT valve in VSC-HVDC[J].Transactions of China Electrotechnical Society，2014，29(8)：235-241.

[3]曾博，唐求，卿柏元，等.基于Nuttall自卷积窗的改进FFT谱分析方法[J].电工技术学报，2014，29(7)：59-65.

Zeng Bo，Tang Qiu，Qing Baiyuan，et al.Spectral analysis method based on improved FFT by Nuttall selfconvolution window[J].Transactions of China Electrotechnical Society，2014，29(9)：59-65.

[4]王兴贵，刘正英.基于载波变幅移相调制方法的串联型微网功率平衡控制[J].电力系统保护与控制，2015，43(13)：38-44.

Wang Xinggui，Liu Zhengying.Series micro-grid power balance control based on carrier amplitude variation and[J].Power System Protection and Control，2015，43(13)：38-44.

[5]徐建，张语勍，李彦斌，等.短时傅里叶变换和S变换用于检测电压暂降的对比研究[J].电力系统保护与控制，2014，12(16)：44-48.Xu Jian，Zhang Yuqing，Li Yanbin，et al.Comparative study of STFT and S transform on detecting voltage sag[J].Power System Protection and Control，2014，12(16)：44-48.

[6]郁祎琳，徐永海，刘晓博.滑窗迭代DFT的谐波电流检测方法[J].电力系统保护与控制，2011，39(13)：78-90.

Yu Yilin，Xu Yonghai，Liu Xiaobo.Study of harmonic current detection based on sliding-window iterative algorithm of DFT[J].Power System Protection and Control，2011，39(13)：78-90.

[7]Jacobsen E，Lyons R.The sliding DFT[J].IEEE Signal Processing Magazine，2003，20(3)：74-80.

[8]Jacobsen E，Lyons R.An update to the sliding DFT[J].IEEE Signal Processing Magazine，2004，21(1)：110-111.

[9]王宏伟.基于傅里叶变换的数字信道化及相关技术[D].西安：西安电子科技大学，2010.

[10]Carlos M O，Ignacio C，Sebastian M，et al.Harmonics measurement with a modulated sliding discrete Fourier transform algorithm[J].IEEE Transactions on Instrumen-tation and Measurement，2014，63(4)：781-793.

[11]周柯，罗安，汤赐，等.一种大功率混合注入式有源电力滤波器的工程应用[J].中国电机工程学报，2007，27(22)：80-86.

Zhou Ke，Luo An，Tang Ci，et al.High-power hybrid injection active power filter’s engineering application[J].Proceedings of the CSEE，2007，27(22)：80-86.

[12]Ni Ruoshui，Li Yunwei，Zhang Ye，et al.Virtual impedance based selective harmonic compensation(VI-SHC)PWM for current source rectifiers[J].IEEE Transactions on Power Electronics，2014，29(7)：3346-3356.

[13]Reza M S，Ciobotaru M，Agelidis V G.Accurate estimation of single-phase grid voltage parameters under distorted conditions[J].IEEE Transactions on Power Delivery，2014，29(3)：138-1146.

[14]Kim J H，Chang T G.Analytic derivation of the finite word-length effect of the twiddle factors in recursive implementation of the sliding DFT[J].IEEE Transactions on Signal Processing，2000，48(5)：1485-1488.

[15]王宏伟.滑动离散傅立叶算法输出稳定性研究[J].电波科学学报，2012，27(4)：773-779.

Wang Hongwei.Output stabilization of sliding discrete Fourier transform algorithm[J].Chinese Journal of Radio Science，2012，27(4)：773-779.

[16]Darwish H A，Fikri M.Practical considerations for recursive DFT implementation in numerical relays[J].IEEE Transactions on Power Delivery，2007，22(1)：42-49.

[17]Duda K.Accurate，guaranteed stable，sliding discrete fourier transform[J].IEEE Signal Processing Magazine，2010，27(6)：124-127.

[18]Neves F A S，Souza H E P，Cavalcanti M C，et al.Digital filters for fast harmonic sequence component separation of unbalanced and distorted three-phase signals[J].IEEE Transactions on Industrial Electronics，2012，59(10)：3847-3859.

[19]Neves S，Arcanjo C，Azevedo S，et al.The SVFT-Based Control[J].IEEE Transactions on Industrial Electronics，2014，61(8)：4152-4160.

[20]Borisov K，Ginn H，Chen G.A computationally efficient RDFT-based reference signal generator for active compensators[J].IEEE Transactions on Power Delivery，2009，24(4)：2396-2404.

[21]Ginn H L，Chen Guangda.Digital control method for grid-connected converters supplied with nonideal voltage[J].IEEE Transactions on Industrial Informatics，2014，10(1)：127-136.

[22]Chen Guangda，Jiang Yingying，Zhou Haiguo.Practical issues of recursive DFT in active power filter based on CPC power theory[C]//Proceedings of Power and Energy Engineering Conference，Wuhan，2009：1-5.

[23]McGrath B P，Holmes D G，Galloway J J H.Power converter line synchronization using a discrete Fourier transform(DFT)based on a variable sample rate[J].IEEE Transactions on Power Electronics，2005，20(4)：877-884.

[24]Yang Junzhe，Liu Chihwen.A precise calculation of power system frequency[J].IEEE Transactions on Power Delivery，2001，16(3)：361-366.

[25]胡广书.数字信号处理——理论、算法与实现[M].3版.北京：清华大学出版社，2012：406-425.

[26]常建平，李海林.随机信号分析[M].北京：科学出版社，2006：82-94.

Research of Finite-Word-Length Effects on the Stability of the Sliding DFT

Liu HuawuHu HaibingXing Yan

(Jiangsu Key Laboratory of New Energy Generation and Power Conversion Nanjing University of Aeronautics and AstronauticsNanjing210016China)

AbstractThe sliding discrete Fourier transform(DFT)can experience instability issues due to the accumulation and amplification of the errors introduced by the finite-word-length effects in real practical discrete systems.In this paper,the quantization noise of A-D,the quantization error of the twiddle factors,and the rounding error of arithmetic operations are taken into consideration to analyze their influences on the stability of the sliding DFT based on the statistical properites of random signals.Based on the detailed analysis,it is revealed that the rounding error of arithmetic operations is the key reason to cause the unstable phenomenon.Both simulation and experimental results validate the theoretical analysis of instability issue of the sliding DFT.To deal with this instability problem,two methods are proposed to eliminate the error accumulation and amplification through swapping the calculation sequences of the sliding DFT.Extensive simulations and experiments are provided to verify the effectiveness of the proposed solutions.

Keywords：Finite-word-length effects，sliding DFT，stability，rounding errors

收稿日期2015-04-02改稿日期2015-07-20

作者简介E-mail：liuhuawu@nuaa.edu.cn(通信作者) E-mail：huhaibing@nuaa.edu.cn

中图分类号：TM935

江苏省产学研联合创新资金前瞻性研究项目资助(BY2014003-12)。

刘华吾男，1989年生，博士研究生，研究方向为电力电子与电力传动。

胡海兵男，1973年生，教授，研究方向为电力电子数字控制装置及电力电子系统集成。