同轴电极的负电晕特里切尔脉冲特性分析

何旺龄　何俊佳　张　锦　万保权

(1.华中科技大学电气与电子工程学院　武汉　430074 2.中国电力科学研究院(武汉)　武汉　430074)

同轴电极的负电晕特里切尔脉冲特性分析

何旺龄1何俊佳1张锦2万保权2

(1.华中科技大学电气与电子工程学院武汉430074 2.中国电力科学研究院(武汉)武汉430074)

摘要利用流体动力学模型，对大气压条件下空气间隙的同轴电极结构进行了负极性电晕放电特性研究，获得了一组规则的特里切尔脉冲。除第一个脉冲外，其他脉冲的幅值均在1.5～2.5 mA。然后，对第一个脉冲(称为第一脉冲)不同发展阶段的空间电场分布和粒子密度分布进行了描述，并讨论了第一脉冲与第二脉冲之间的死区时间内不同时刻负离子密度的变化过程及其对阴极表面电场的影响作用，最后，对第二脉冲发展前后空间电场分布、电子密度分布和负离子密度分布及其变化规律进行了进一步的描述。仿真表明，随着负离子在电场力的作用下逐渐向外迁移，导线表面电场强度开始恢复，但其恢复速度在负离子远离导线的过程中逐渐变缓。同时，当导线表面电场强度恢复至低于初始拉普拉斯场强的某一特定值时，新的脉冲就开始发生，第二脉冲发生时空间电场、电子密度及负离子密度的最大值均小于第一脉冲。

关键词：负电晕特里切尔脉冲空间电场分布粒子密度

0引言

我国正在大力发展特高压交直流输电线路[1，2]，随着输电线路电压等级的提高，导线周围的电晕放电现象变得愈加明显，强烈的电晕放电现象会引起线路的绝缘劣化和电晕损失增大等问题，影响线路的输送安全和输送效率[3-6]。同时，也会导致一些环境效应，如电磁干扰和可听噪声等[7-9]。此外，电晕放电也被人们用来进行空气净化和污水处理等工业应用[10]。而特里切尔脉冲放电是电晕放电的重要组成部分，对解释电晕放电现象起着至关重要的作用。因此，有必要对负极性特里切尔脉冲进行分析研究。

特里切尔于1938年首次发现，在负极性电晕放电条件下，存在一种规则的电晕电流脉冲族，通常表现为上升时间较快(小到ns级)，脉冲幅值较小，持续时间较短[11]。此后，人们对特里切尔脉冲进行了大量的理论研究和实验研究。在实验研究方面，文献[12]对不同气体条件下的特里切尔脉冲进行了测量，认为特里切尔脉冲只存在于电负性气体之中。文献[13]在空气条件下，采用针板电极结构对特里切尔脉冲进行了大量的实验测量研究，建立了脉冲频率、平均电晕电流与施加电压、针尖的曲率半径以及针板距离之间的相互关系。文献[14]发现在给定电极条件下，特里切尔脉冲的形成过程与电压、气压以及外电路并联电容并无关系。

在研究气体放电机理方面，由于空气放电等离子体测量技术的限制，许多放电特征参数还不能完全通过实验来获取，所以国内外很多学者利用数学手段对特里切尔脉冲进行建模分析和研究。近年来，P.Sattari等[15，16]利用针板结构，提出一种新的二维特里切尔脉冲仿真模型，讨论了不同施加电压条件下特里切尔脉冲频率的变化规律，并与W.L.Lama等的实测数据进行了对比分析。T.N.Tran等[17]提出了基于轴对称的有限元模型对负极性电晕放电进行仿真分析，对不同施加电压及不同二次发射系数对特里切尔脉冲频率及幅值的影响进行了分析研究，并与实验数据进行了对比分析。尹晗等[18]建立了二维时域模型对线板结构的特里切尔脉冲进行仿真分析，其中利用有限元方法进行泊松方程求解，利用有限体积法进行对流方程求解。伍飞飞等[19，20]基于流体动力学模型，提出了一种考虑不同化学碰撞反应和光电离的混合数值模型，并对针板结构下的特里切尔脉冲进行了仿真分析。

上述学者在进行负极性电晕放电的数值计算时，对特里切尔脉冲族中第一脉冲的微观过程进行了建模和仿真分析，并对整个脉冲族的宏观特性(如脉冲幅值和脉冲频率)进行了讨论。基于前人的研究成果，本文采用流体模型，利用有限元方法，对特里切尔脉冲发展过程中的3种带电粒子进行了建模仿真，讨论了第一脉冲不同发展阶段的空间电场分布和粒子密度分布，并对死区时间内空间电场和负离子密度的变化规律进行了细致的描述，最后讨论了第二个脉冲起始前后电场、电子密度和负离子密度的变化过程。

1数值模型建立

1.1控制方程

本文基于流体动力学模型，对负极性电晕放电过程中电子、正离子和负离子的对流扩散运动及产生和消失过程进行了数学建模，并与考虑空间电荷影响的泊松方程进行耦合求解，从而模拟特里切尔脉冲的发展过程。泊松方程和连续性方程见式(1)～式(4)。

泊松方程

(1)

连续性方程

(2)

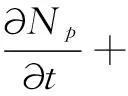
(3)

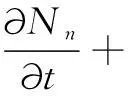
(4)

式中，Φ为电势，V；t为时间，s；Ne、Np、Nn分别为电子、正离子和负离子的密度，1/m3；e为单位电荷量，1.69×10-19C；ε0为真空介电常数，8.854×10-12F/m；εr为相对介电常数，取值为1；We、Wp、Wn分别为电子、正离子和负离子的运动速度矢量，m/s；α为空气在标准大气压条件下的汤森电离系数，1/m；η为吸附系数，1/m；βep为电子-正离子复合率；βnp为正负离子复合率；De为电子扩散系数。

相关参数的具体计算方法如下所示[21]。

(5)

(6)

(7)

Wp=μpE，Wn=-μnE

(8)

βep=βnp=2.2×10-12m3/s

(9)

De=1.28×10-3m2/s

(10)

式中，E为空间电场强度矢量，V/m；δ为相对空气密度，取值为1；μp、μn分别为正离子和负离子迁移率，μp=1.4×10-4m2/(V·s)，μn=1.8×10-4m2/(V·s)。

1.2计算模型

图1为负极性电晕放电模型，其中，导线半径为0.05 cm，同轴电极外半径为20 cm，导线施加电压为-30 kV，外电极接地。考虑到整个区域计算量大，而导线电离层很薄的情况[21]，本文对计算区域进行了简化，在导线周围设置了圆形人工边界，边界半径为子导线半径的20倍，即1 cm。人工边界的电位通过静电场计算设置为-15 kV。

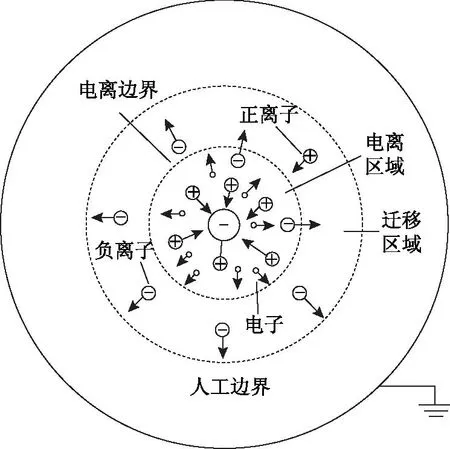
图1　负极性电晕放电模型Fig.1　Schematic diagram of negative corona discharge

电子二次发射是维持负极性电晕放电进一步发展的重要机理，而目前对于电子二次发射过程有不同的描述机理，包括阴极表面场强较大导致的场致发射、放电等离子体中光子辐射产生的电子发射以及正离子碰撞阴极表面产生的电子发射[17]。文献[17，18]均认为正离子碰撞阴极是负极性电晕放电持续向前发展的关键原因。因此，本文在仿真时仅考虑正离子碰撞阴极产生二次电子这一过程。

电晕电流计算采用文献[17]提出的方法，即电晕电流为导线表面的带电粒子通量与导线表面感应电荷变化量的环路积分。

(11)

式中，Is为电晕电流，A；n为阴极表面的法向量；dS为阴极表面的面积微元；σca为阴极表面的电荷密度，当阴极为金属电极时，其计算公式为

σca=-n(ε0εrEcathode)

(12)

式中，Ecathode为阴极表面的电场强度矢量，V/m。

1.3仿真模型及边界条件

本文进行仿真计算时，具体的网格剖分结构图如图2和图3所示。在导线表面附近区域及放电通道可能发展到达区域中，电子密度和电场强度等物理量相对于其他区域具有较大的数值及梯度，因此该部分区域的网格划分非常细。在计算过程中，模型总共划分为161 080个网格，平均网格质量为0.982 8。

图2　计算几何结构网格剖分图(总体)Fig.2　Meshed simulation geometry(overall)

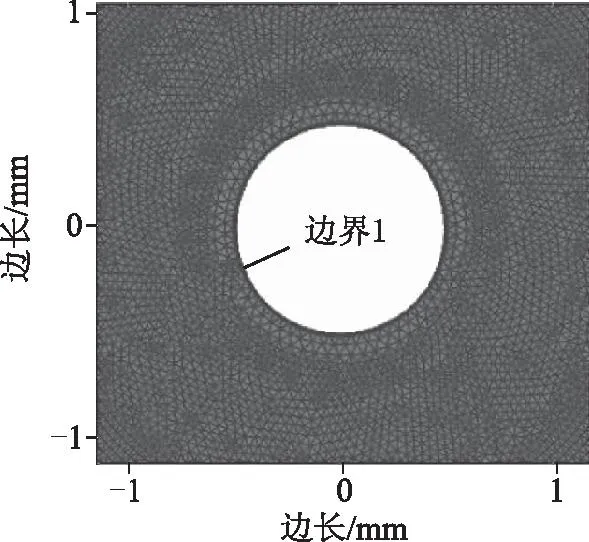
图3　计算几何结构网格剖分图(细化)Fig.3　Meshed simulation geometry(enlarged)

同时，对于流体模型来说，边界条件的设置至关重要，本文仿真时，具体的边界条件设置如表1所示。其中，γ为电子的二次发射系数，取值为0.01[18]；De为电子扩散系数，取值为1.28×10-3m2/s;Dp和Dn分别为正离子和负离子扩散系数，取值为0[18]。

表1　边界条件

2仿真结果及讨论

本文主要基于Comsol Multiphysics有限元分析软件的流体模块进行建模计算，计算的环境条件为300 K和1个标准大气压。在下列各仿真图中，电流以及电场幅值均为绝对值。

2.1特里切尔脉冲仿真波形

图4为一组特里切尔电流脉冲，在500 μs的时间内呈现出80个连续脉冲。图5为脉冲族的局部放大图。图6为单个电晕电流脉冲。

由图4～图6可见，仿真的电流脉冲符合特里切尔脉冲的基本特性，除第一脉冲外，其他脉冲的幅值和频率均比较规则，脉冲峰值在1.5～2.5 mA，与文献[21]中测量的脉冲幅值基本一致。单个脉冲呈较快的上升时间和短的持续时间，在一段死区时间后，新的脉冲重新发生。

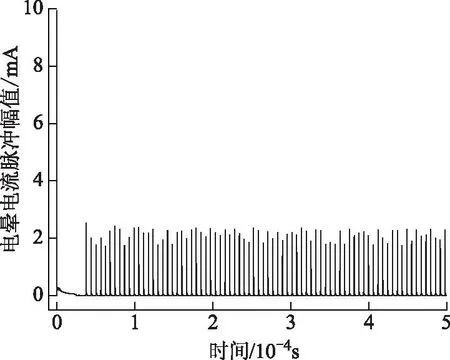
图4　仿真的特里切尔脉冲Fig.4　The simulated Trichel pulses

图5　特里切尔脉冲局部放大图Fig.5　The partial enlarged Trichel pulses

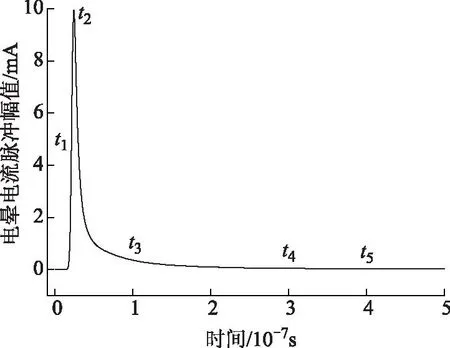
图6　第一个特里切尔脉冲Fig.6　The first Trichel pulse

通过图4发现，第一脉冲的幅值较大，其后的死区时间也长于后续脉冲中较规则的死区时间，这种现象在文献[15，18]中均有描述。引起这一现象的主要原因是：仿真开始时，由于没有空间电荷的抑制作用，第一脉冲发生时的导线表面场强要大于后续脉冲，从而导致第一脉冲发生时电离区的电离程度比较强烈，产生的空间电子和正负离子密度较大，从而使得第一脉冲幅值较大。由于第一脉冲产生的离子较多，导致脉冲发生后，空间离子对电场的抑制作用比后续离子强烈，空间电场减小程度较大，离子的移动速度缓慢，导致导线表面电场恢复至起晕场强的时间被拉长，从而使得整个死区时间变长。

2.2第一脉冲的空间电场分布特性

为了更好地理解特里切尔脉冲的发展过程，本文对第一脉冲不同发展阶段的空间电场分布进行了分析讨论。如图6所示，t1～t5所对应的时刻分别为16 ns、24 ns、100 ns、300 ns和400 ns。不同时刻的空间电场分布如图7所示。

图7　第一脉冲不同时刻电场分布Fig.7　Electric field distribution at different times during the first Trichel pulse

可以看出，在0时刻，电场分布为不受空间电荷影响的拉普拉斯(Laplace)场。随着负极性电晕脉冲的起始与发展，碰撞电离产生的大量正离子向阴极方向移动，使得正离子与阴极之间的区域场强发生畸变。正离子在碰撞阴极之后发射出的二次电子加剧了阴极附近的电离程度，从而在该区域产生了大量的带电粒子，形成了包含电子云和正负离子云的等离子体区域。更加靠近阴极的正离子云使得阴极与等离子体之间的电场强度急剧增大，这一现象可从t1、t2时刻的电场分布图看出。由于受空间电荷场反方向影响，等离子体通道内的区域场强很小。

此后，随着等离子体头部越来越靠近阴极，高场强的电离区域变得非常小，最后，没有足够的高场强区域进行碰撞电离，脉冲停止发展，正离子被阴极逐渐吸收，阴极表面及附近的场强受到负离子和电子的抑制作用开始下降。

2.3第一脉冲的空间粒子分布特性

电子在脉冲放电过程中起至关重要的媒介作用，由于其运动速度较快，在与中性分子发生碰撞时，承担能量传递的功能。而空间分布的负离子对导线表面电场有抑制作用。因此，下面对两种带电粒子在第一脉冲发展不同阶段的空间密度分布进行了描述。

由图8和图9可以看出，在脉冲起始、等离子体头部向阴极发展的过程中，形成了大量的电子和负离子，两者的密度分别达到1019m-3和1018m-3数量级。随后在等离子体停止向前发展，逐渐消散的过程中，电子和负离子密度开始下降，同时由于电场力的作用，两者向远离导线的方向迁移。

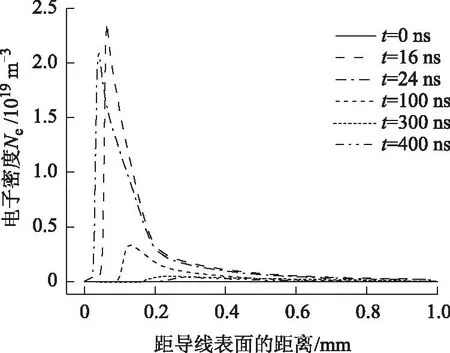
图8　第一脉冲不同时刻空间电子密度分布Fig.8　Electron density distribution at different times during the first Trichel pulse

图9　第一脉冲不同时刻空间负离子密度分布Fig.9　Negative ion density distribution at different times during the first Trichel pulse

2.4死区时间内的带电粒子特性

图10和图11分别为第一个死区时间内不同时刻的负离子和空间电场分布。由图10可以看出，随着时间的增加，负离子逐渐向外扩散，由于在扩散过程中与空间分布正离子的复合作用，负离子密度逐渐降低。从2 μs发展到8 μs时，最大负离子密度由2.03×1017m-3下降到4.5×1016m-3。通过图11可以看出，随着负离子向外迁移和复合，其对阴极表面及附近区域的电场抑制作用开始减弱，该区域的电场逐渐上升。

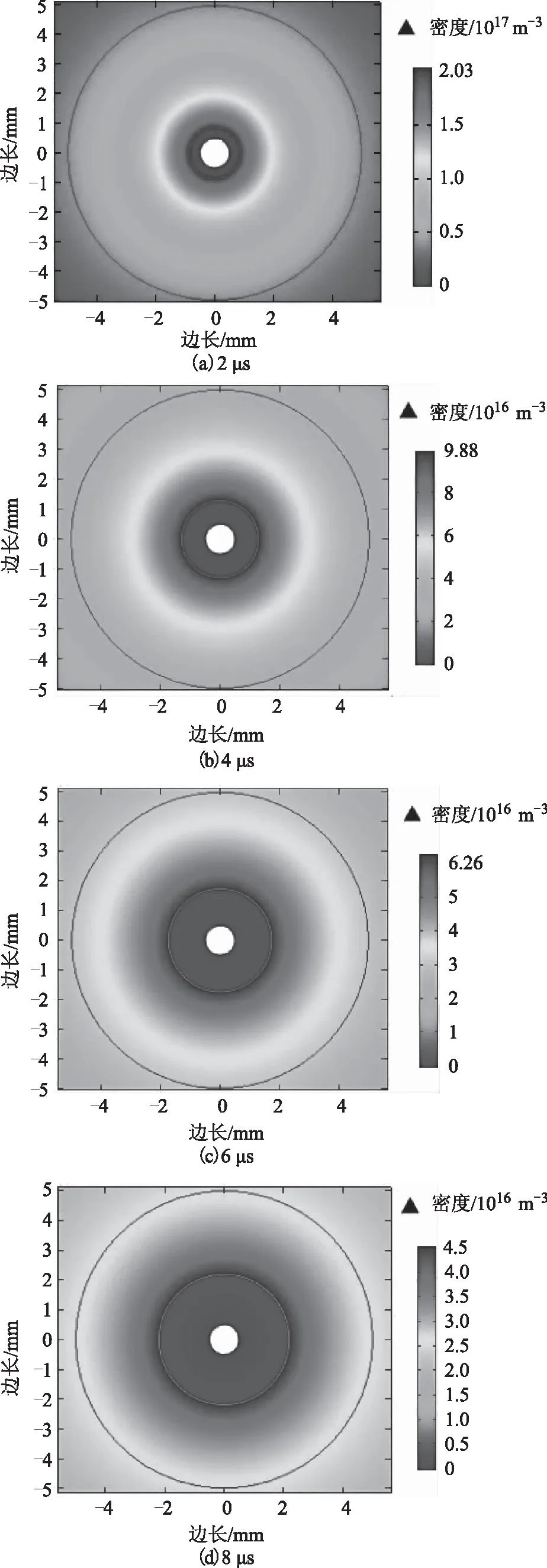
图10　死区时间不同时刻空间负离子二维分布(1/m3)Fig.10　Negative ion density distribution at different times during the dead time(1/m3)

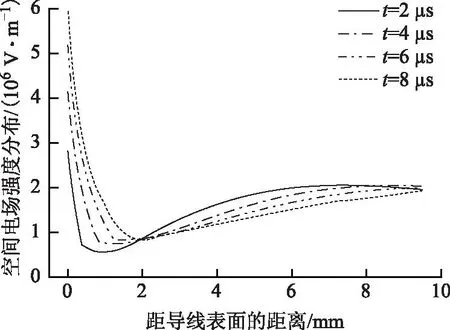
图11　死区时间不同时刻空间电场分布Fig.11　 Electric field distribution at different times during the dead time

图12为第二个脉冲发展前不同时刻的空间电场变化图。可以看出，在t=0.1 μs时，第一脉冲逐渐停止发展，阴极表面的场强开始下降。而后，随着负离子的迁移和复合，该区域电场逐渐恢复。当负离子距离导线表面越来越远时，场强的恢复速度也逐渐放缓。可以看出，在t=10 μs与t=20 μs时，阴极表面及附近区域的场强分布几乎重合，表面场强仅从6.32×106V/m恢复至6.37×106V/m。这主要是由于随着负离子向外扩散，其所处空间电场强度越来越小，由式(8)可知，当电场减小时，负离子运动速率降低，从而导致场强恢复速度变慢。这一过程持续到导线表面场强达到起晕场强，第二次脉冲放电开始。

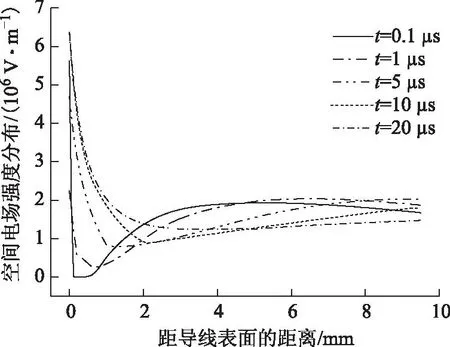
图12　不同时刻电场分布Fig.12　Electric field distribution at different times

2.5新的脉冲起始及发展

图13～图15分别为第二脉冲起始、发展及终止的不同时刻空间电场分布和电子、负离子密度分布。由图13可以看出，当新的脉冲起始时，阴极表面场强并未恢复至初始外加电压条件下的Laplace场。在36.9 ～37.1 μs时，二次脉冲发生，碰撞电离形成的等离子体向阴极发展，阴极附近区域的电子密度和负离子密度急剧增大，该区域的场强也发生较大的畸变。

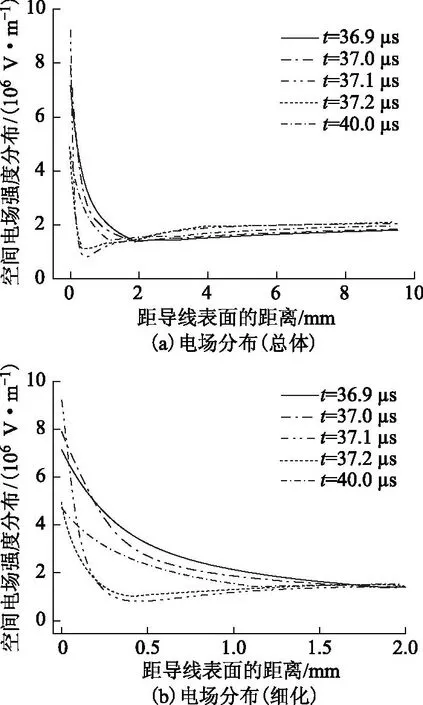
图13　第二个脉冲发展不同时刻空间电场分布Fig.13　Electric field distribution at different times during the second pulse

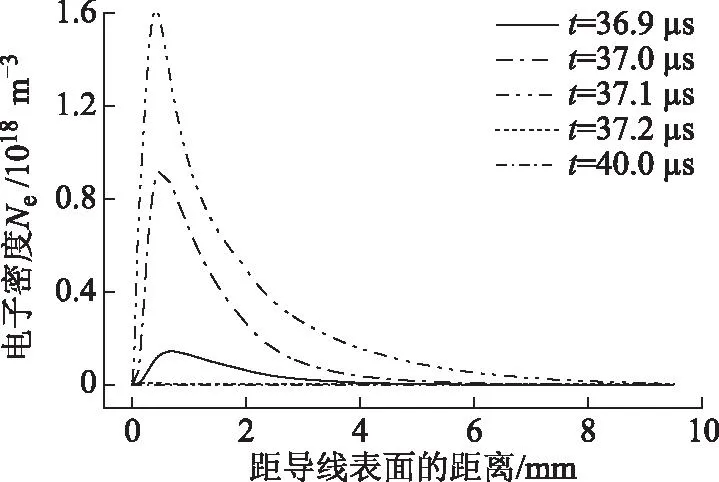
图14　第二个脉冲发展不同时刻空间电子密度分布Fig.14　Electron density distribution at different times during the second pulse

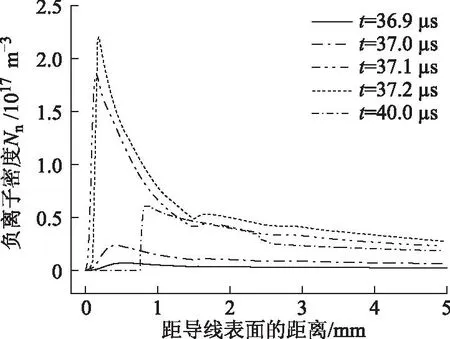
图15　第二个脉冲发展不同时刻空间负离子密度分布Fig.15　Negative ion density distribution at different times during the second pulse

随着二次脉冲结束，空间电子逐渐消散，负离子在电场力的作用下开始向外迁移，导线表面电场也逐渐恢复。一段死区时间后，新的脉冲开始重复发生。

3结论

本文建立了基于有限元的流体动力学模型，对同轴电极结构的负极性特里切尔脉冲进行了数值仿真。通过计算，在500 μs的时间长度内，总共仿真出80个连续规则的特里切尔电流脉冲，除第一个脉冲外，脉冲幅值均在1.5～2.5 mA之间。

通过描述第一个脉冲不同发展阶段的电场、电子和负离子密度变化情况，可以得出，当碰撞电离产生的等离子体向阴极发展时，等离子体头部电离程度非常强烈，场强、电子和负离子密度较大，其中，电子密度比负离子密度高出一个数量级。第一脉冲发展结束后，负离子逐渐向外扩散，导线表面的场强开始恢复。该过程一直持续到导线表面场强达到起晕场强，新的电晕脉冲发生。通过观察新脉冲发展前后导线表面场强的变化可知，后续脉冲在起始时，导线表面场强不能恢复至无空间电荷影响的初始Laplace场强。同时，后续脉冲发生时空间电子密度和负离子密度要小于第一脉冲。

参考文献

[1]刘振亚.特高压电网[M].北京：中国经济出版社，2006.

[2]Huang Daochun，Shu Yinbiao，Ruan Jiangjun，et al.Ultra-high-voltage transmission in China：developments，current status，and future prospects[J].Proceeding of the IEEE，2009，97(3)：553-554.

[3]Maruvada P S.Corona performance of high-voltage transmission lines[M].Baldock：Research Studies Press Ltd.，2000.

[4]刘阳，崔翔，卢铁兵，等.湿度对绞线正极性电晕电流脉冲及其无线电干扰影响的试验[J].电工技术学报，2015，30(3)：79-89.

Liu Yang，Cui Xiang，Lu Tiebing，et al.Experimental investigation of humidity impact on positive corona current pulse and its radio interference of stranded conductors[J].Transactions of China Electrotechnical Society，2015，30(3)：79-89.

[5]乔骥，邹军，袁健生，等.采用有限差分求解高压直流输电线路空间离子流场的新方法[J].电工技术学报，2015，30(6)：85-91.

Qiao Ji，Zou Jun，Yuan Jiansheng，et al.A new finite difference based approach for calculating ion flow field of HVDC transmission lnes[J].Transactions of China Electrotechnical Society，2015，30(6)：85-91.

[6]胡琴，吴执，舒立春，等.交流电场下水滴对导线电晕特性的影响[J].电工技术学报，2015，30(18)：237-245.

Hu Qin，Wu Zhi，Shu Lichun，et al.The crona caracteristics of the cnductor atached with wter dops under AC electrical feld[J].Transactions of China Electrotechnical Society，2015，30(18)：237-245.

[7]谢莉，赵录兴，陆家榆，等.有限长高压直流输电线路无线电干扰电磁场的计算方法研究[J].电工技术学报，2016，31(1)：96-102.

Xie Li，Zhao Luxing，Lu Jiayu，et al.Study on the clculation mthod for rdio interference electromagnetic field of HVDC transmission line with finite length[J].Transactions of China Electrotechnical Society，2016，31(1)：96-102.

[8]刘云鹏，朱雷，律方成，等.特高压电晕笼直流分裂导线正极性电晕起始特性分析[J].电工技术学报，2013，28(1)：73-79.

Liu Yunpeng，Zhu Lei，Lü Fangcheng，et al.Analysis of the positive corona onset characteristic of the bundle conductors in the UHV corona cage[J].Transactions of China Electrotechnical Society，2013，28(1)：73-79.

[9]何旺龄，万保权，刘震寰，等.特高压交流试验线段的无线电干扰特性研究及长线路预测[J].高电压技术，2014，40(12)：3953-3960.

He Wangling，Wan Baoquan，Liu Zhenhuan，et al.Radio interference characteristics of UHVAC test lines and prediction for long lines[J].High Voltage Engineering，2014，40(12)：3953-3960.

[10]Lin Lie，Zhang Peng，Wang Yongqing.Analysis of instabilities in non-equilibrium plasmas[J].Chinese Physics Letters，2004，21(10)：1993-1996.

[11]Trichel G W.The mechanism of the negative point to plane corona near onset[J].Physics Review，1938，54(12)：1078-1084.

[12]Loeb L B.The mechanism of the trichel pulses of short time duration in air[J].Physical Review，1952，86(2)：256-257.

[13]Lama W L，Gallo C F.Systematic study of the electrical characteristics of the Trichel current pulses from negative needle-to-plane coronas[J].Journal Applied Physics，1974，45(1)：103-13.

[14]欧阳吉庭，张子亮，张宇，等.空气负电晕Trichel 脉冲特性的实验研究[J].高电压技术，2014，40(4)：1194-1200.

Ouyang Jiting，Zhang Ziliang，Zhang Yu，et al.Experimental study on the characteristics of negative-corona Trichel pulses in air[J].High Voltage Engineering，2014，40(4)：1194-1200.

[15]Sattari P，Castle G S P，Adamiak K，et al.Numerical simulation of Trichel pulses in a negative corona discharge in air[J].IEEE Transactions on Industry Applications，2011，47(4)：1935-1943.

[16]Sattari P，Castle G S P，Adamiak K，et al.Trichel pulse characteristics—negative corona discharge in air[J].Journal of Physics D：Applied Physics，2011，44(15)：155502-155512.

[17]Tran T N，Golosnoy I O，Lewin P L，et al.Numerical modelling of negative discharges in air with experimental validation[J].Journal of Physics D：Applied Physics，2011，44(1)：015203.

[18]Yin Han，Zhang Bo，He Jinliang，et al.Modeling of Trichel pulses in the negative corona on a line-to-plane geometry[J].IEEE Transactions on Magnetics，2014，50(2)：473-476.

[19]伍飞飞，廖瑞金，杨丽君，等.棒-板电极直流负电晕放电特里切尔脉冲的微观过程分析[J].物理学报，2013(11)：348-357.Wu Feifei，Liao Ruijin，Yang Lijun，et al.Analysis on micro process of DC negative Trichel pulses in a bar-plane electrode[J].Acta Physica Sinica，2013(11)：348-357.

[20]廖瑞金，伍飞飞，刘康淋，等.棒-板电极直流负电晕放电脉冲过程中的电子特性研究[J].电工技术学报，2015，30(10)：319-329.

Liao Ruijin，Wu Feifei，Liu Kanglin，et al.Simulation of characteristics of electrons during a pulse cycle in Bar-Plate DC negative corona discharge[J].Transactions of China Electrotechnical Society，2015，30(10)： 319-329.

[21]尹晗.直流输电线路高频电晕电流与无线电干扰的转换关系[D].北京：清华大学，2014.

Characteristics of Negative Corona Trichel Pulses in a Coaxial Electrode System

He Wangling1He Junjia1Zhang Jin2Wan Baoquan2

(1.School of Electrical and Electronic EngineeringHuazhong University of Science and Technology Wuhan430074China 2.China Electric Power Research Institute(Wuhan)Wuhan430074China)

AbstractIn this paper,the characteristics of negative corona discharge in air at atmospheric pressure are studied by using the hydrodynamic drift-diffusion model with a coaxial electrode system,and a set of regular Trichel pulses is obtained.It is found that the pulse amplitude is between 1.5 mA and 2.5 mA except the first one.Then the distributions of the electric field,the ion densities at different stages during the first pulse are plotted.The distribution of the negative ion density and its influence on the conductor surface electric field are discussed during the dead time between the first pulse and the second pulse.After that,the distributions of the electric field,the electron and negative ion densities around the second pulse are plotted.The simulation results show that the electric field at the conductor surface increases when the negative ions remove from cathode under the influence of electric field force;and the recovery velocity of electric field slows down when the negative ions move away.Besides,before the electric field at the conductor surface recovers to its original Laplacian field strength,the next new pulse begins to happen.It is also found that the maximum values of the electric field,the electron and negative ion densities are reduced during the second pulse comparing with those in the first pulse.

Keywords：Negative corona，Trichel pulse，electric field distribution，ion density

收稿日期2015-04-15改稿日期2015-07-05

作者简介E-mail：wanglinghe88@gmail.com(通信作者) E-mail：h-junjia@vip.sina.com

中图分类号：TM723

国家重点基础研究发展(973)计划资助项目(2011CB209402)。

何旺龄男，1988年生，博士研究生，研究方向为交流输电线路的电晕放电与电磁环境。

何俊佳男，1968年生，教授，博士生导师，研究方向为电弧电接触、高电压与绝缘技术以及脉冲功率技术。