基于自抗扰控制的永磁同步电机位置伺服系统一体化设计

左月飞　张　捷　刘　闯　张　涛

(南京航空航天大学自动化学院　南京　210016)

基于自抗扰控制的永磁同步电机位置伺服系统一体化设计

左月飞张捷刘闯张涛

(南京航空航天大学自动化学院南京210016)

摘要为解决位置环采用常规二阶自抗扰控制(ADRC)的永磁同步电机伺服系统中速度不可控的问题，提出一种位置、速度控制器一体化设计方法。首先，分析了常规二阶ADRC位置控制的设计方法以及存在的问题；其次，借鉴滑模控制的一体化设计思想，综合设计系统的外环控制器，采用偏差反馈的算法对转速进行限幅，实现了四段式位置伺服控制，从而解决了常规二阶ADRC中速度不可控的问题。所提方法在最高转速进行限幅的基础上，能够实现电机的最速位置定位，而且对不同的位置给定和不同的转速限幅条件均适用。仿真和实验结果验证了其有效性与可行性。

关键词：自抗扰控制永磁同步电机位置伺服系统一体化设计

0引言

在雷达、电动舵机、机器人等伺服应用场合，永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)以其高功率密度、高转矩/惯量比和高效率等优点逐渐成为主流之选。传统的PMSM位置伺服系统大多采用三环线性结构，由外至内分别为位置环、转速环和电流环，其中位置环大多采用P控制器，转速环和电流环大多采用PI控制器[1]。而PMSM是一典型的多变量、强耦合、时变的非线性控制对象，因此传统的线性PID控制难以满足高性能的要求。近年来，随着永磁同步电机非线性控制理论的发展，多种先进的复杂控制策略(如非线性PID[2]、自适应控制[3，4]、滑模变结构控制[5，6]、时间最优控制[7]和智能控制[8，9]等)被应用于PMSM伺服系统中。然而这些非线性控制策略对处理器要求较高或存在抖振等问题，还有待进一步改进。

自抗扰控制(Active Disturbance Rejection Control，ADRC)是由中科院韩京清研究员提出的一种新型非线性实用控制方法[10-12]，能够统一观测系统的内外扰动并加以补偿，并采用非线性状态误差反馈实现误差的快速收敛，具有很好的动、静态特性。因此在永磁同步电机控制领域，自抗扰控制已得到了广泛研究[13-18]。

目前，基于自抗扰控制的PMSM位置伺服系统通常采用位置-电流双环结构，位置控制器设计为二阶自抗扰控制器，电流环仍可采用PI控制器[15-18]。然而，由于省去了转速环，使得这种控制方式存在速度不可控的问题，这在实际运行中将会给电机安全带来隐患。自抗扰控制系统中，通常为位置给定信号安排过渡过程，这虽然能够在位置定位时对电机转速起到限制作用，但在跟踪连续变化的位置信号(例如正弦信号)时却会造成响应滞后的不利影响，使得系统的跟踪性能变差[15]。

滑模控制由于同样采用位置-电流双环结构，也存在转速不可控的问题，由此提出了位置速度一体化设计的解决方法[6，19-21]。采用先速度控制后位置控制的思想，将位置响应过程分为加速段、恒速段、减速段和位置接近段4个阶段，从而解决了双环系统中速度不可控的问题。但滑模控制的一体化设计需要设计多个滑模面并进行切换，易使系统振荡，而且还必须对滑模抖振问题采用有效的抑制策略。

本文在文献[15-17]的基础上，借鉴滑模控制的一体化设计思想，提出了一种基于二阶自抗扰控制器的位置速度一体化设计方法。首先推导了常规位置环二阶自抗扰控制系统下最高转速与系统阶跃响应时间的关系，指出系统存在超速与响应快速性相矛盾的问题，而后提出转速限幅的方法，最后通过仿真和实验验证了所提方法的有效性与可行性。

1常规的位置环ADRC设计

1.1PMSM的数学模型

本文的研究对象是一台表贴式永磁同步电机，其在转子磁场定向的同步旋转坐标系(d-q坐标系)下的机械运动方程为

(1)

式中，θ为转子位置角，rad；Ω为机械角速度，rad/s；J为系统的转动惯量，kg·m2；B为系统的粘滞摩擦系数，N·m/(rad/s)；TL为负载转矩，N·m；Kt为转矩常数，N·m/A。

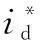
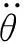
=bu+a(t)

(2)

选择转子位置角θ为状态变量x1，机械角速度Ω为状态变量x2，将总和扰动a(t)扩张为一个新的状态变量x3，则PMSM伺服系统状态方程变为

(3)

1.2误差反馈控制律设计

定义e1=θ*-θ，e2=dθ*/dt-Ω，其中θ*为位置给定信号。假设d2θ*/dt2=0，则系统的误差状态方程为

(4)

采用最速反馈控制律fhan(e1，e2，r，h)作为非线性状态误差反馈律(Nonlinear State Error Feedback，NLSEF)，即系统以允许的最大加速度到达给定位置，则期望的误差收敛方式为

(5)

式中，函数fhan的计算公式为

(6)

式中，r为控制量可取的最大值；h为采样周期；sgn(x)为符号函数。

由式(4)和式(5)可得控制量为

(7)

式(7)中存在未知扰动项x3，因此需要设计状态观测器来观测扰动并加以补偿。

1.3三阶线性扩张状态观测器设计

对式(3)表示的系统建立三阶线性扩张状态观测器(Extended State Observer，ESO)，为

(8)

由式(3)和式(8)可得ESO对各状态的估计为

(9)

式中，λ3(s)为ESO的特征多项式，λ3(s)=s3+β1s2+β2s+β3。

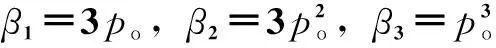
由式(9)可看出，ESO在阶跃扰动下是渐进收敛的，且收敛速度随po的增大而加快。通过ESO观测出总和扰动，则可将式(7)的状态变量x3替换为z3，可得控制量为

(10)

考虑电流限幅，则实际控制量为

(11)

用ESO观测得到的位置角z1和角速度z2分别代替x1和x2作为反馈可减小系统噪声[22]。同时，为了避免系统在有噪声情况下存在稳态抖振，可将离散最速控制函数中的步长h改为稍大的h0(如取h0=10h)[11]。于是，得到常规的位置环二阶自抗扰控制器结构框图如图1所示，基于矢量控制的PMSM位置伺服系统结构框图如图2所示。

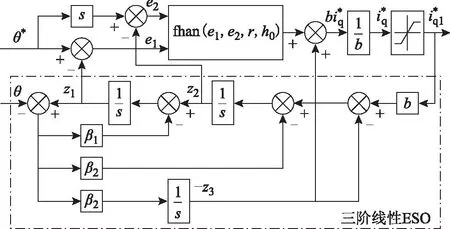
图1　常规位置环二阶自抗扰控制器Fig.1　Conventional second-order ADRC controller

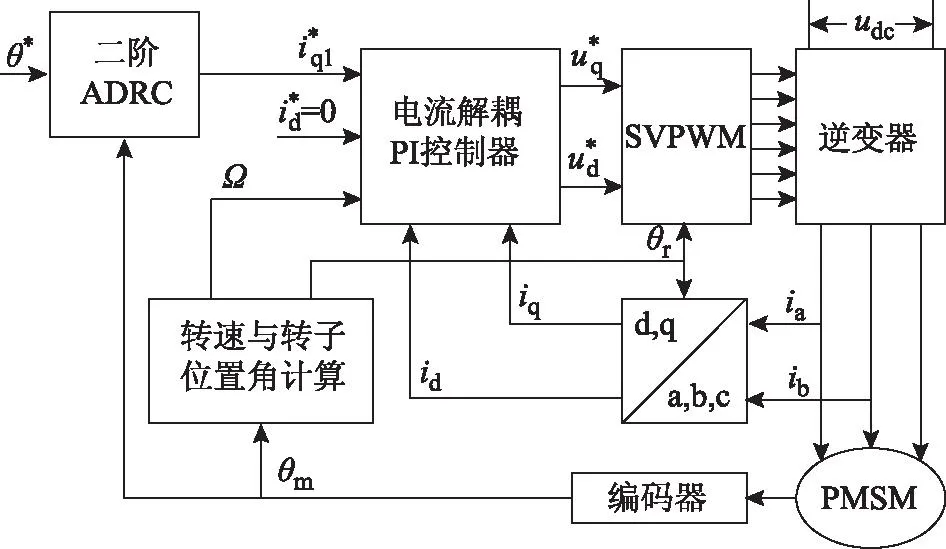
图2　基于矢量控制的PMSM位置伺服系统结构框图Fig.2　Second-order ADRC servo system of position loop

2基于ADRC的位置速度一体化设计

2.1常规位置环ADRC存在的问题

在Matlab/Simulink中搭建仿真模型，采用常规的位置环二阶自抗扰控制器，仿真步长h=0.1 ms。仿真中所用的永磁同步电机参数如表1所示。

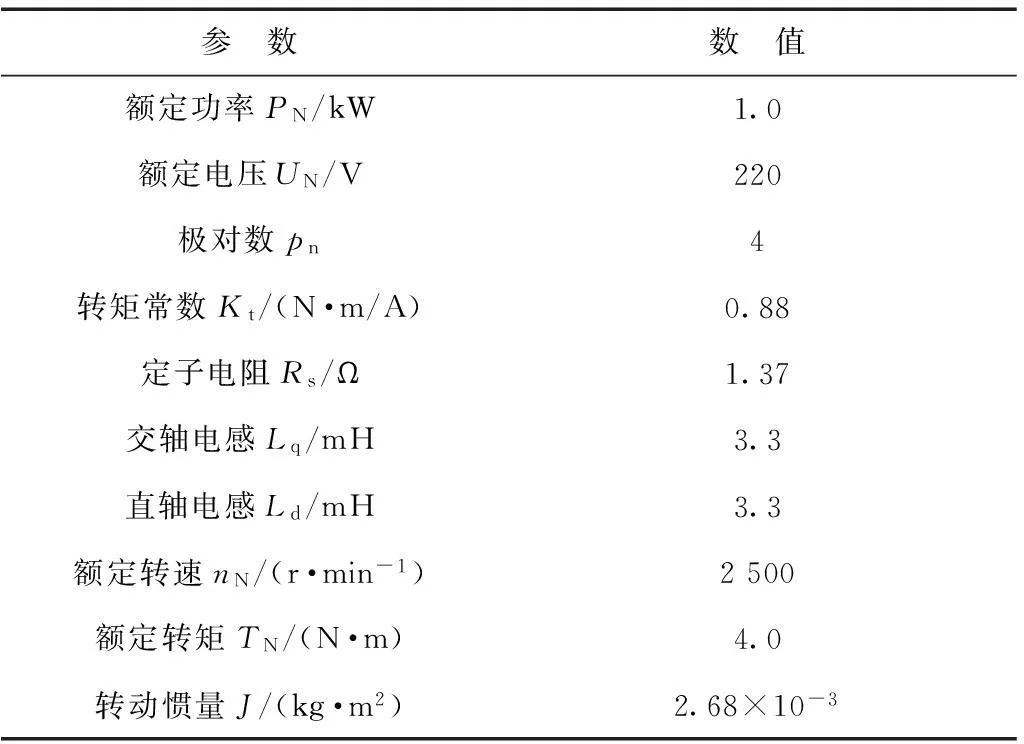
表1　电机参数

取r=1 047，即角加速度β为1 047 rad/s，则位置给定θref与响应时间T和最高转速nm的关系为

(12)

(13)

取h0=10h=1 ms，分别给定10°、90°和150°时，位置伺服系统的位置定位及速度运行曲线如图3所示。由图3可看出，在该控制方式下，由于采用了最速反馈控制，电机在允许的最大加、减速度条件下以最短时间无超调地达到稳定状态。但是，当给定位置较大时，则可能使电机转速远超过允许的最高转速，从而给系统的安全运行带来隐患。由式(12)和式(13)可计算得3种情况下的最高转速分别为129 r/min、387 r/min和500 r/min。如果系统允许的最高转速为150 r/min，则图3b和图3c中转速已超出范围。由于h0≠h，因此仿真结果与理论计算结果存在较小偏差。

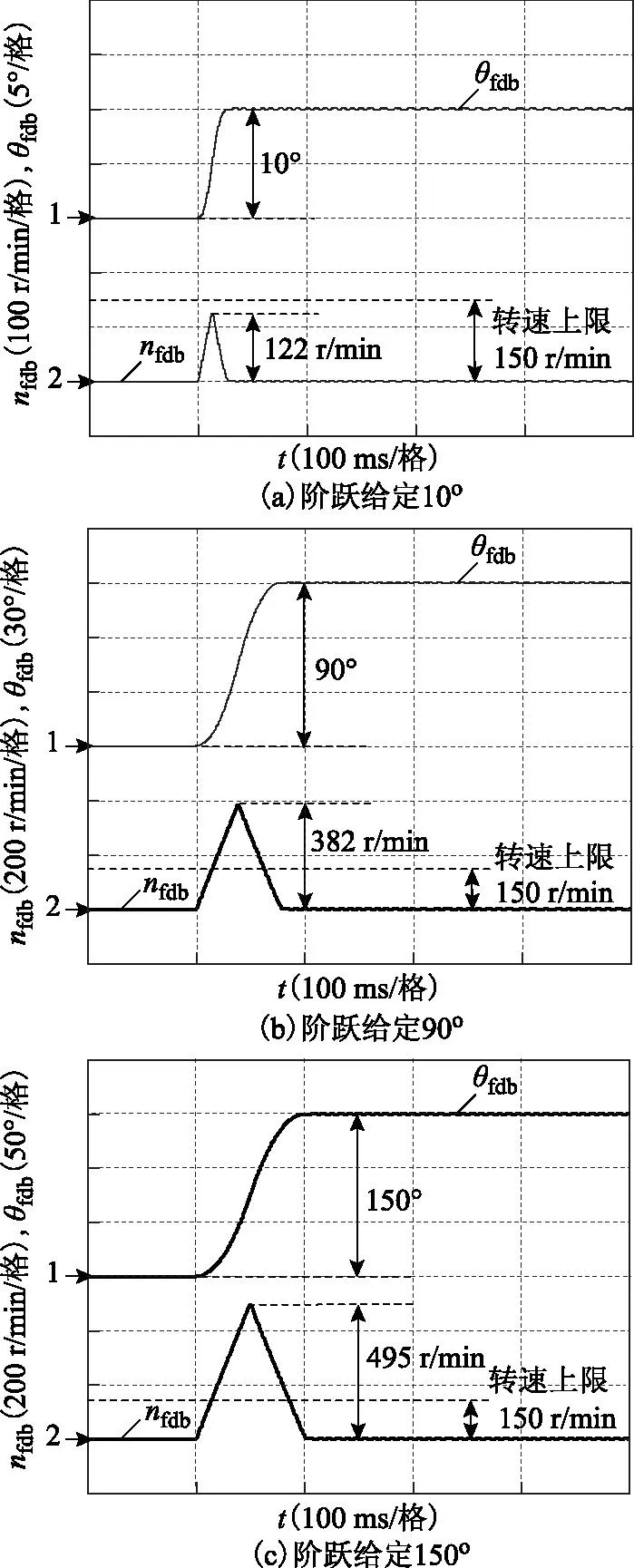
图3　常规ADRC位置伺服系统运行曲线Fig.3　Position response for conventional ADRC servo system

2.2位置速度一体化控制器设计思想

位置速度一体化设计是为解决传统位置伺服滑模控制中速度不可控问题而提出的[19，20]，采用先速度控制后位置控制的思想，将位置响应过程分为加速段、恒速段、减速段和位置接近段4个阶段，如图4所示。

图4　四段式位置伺服控制速度曲线Fig.4　Four-section speed control mode for servo system

在滑模控制中，采用一体化设计思想能够解决速度不可控的问题，但需在多个滑模面中进行切换，易使系统振荡，而且还需要对滑模抖振问题进行抑制。而对于采用位置环二阶ADRC的PMSM伺服系统来说，由于采用最速反馈控制律，电机以允许的最大加、减速度运行，因此只需对电机运行的最高转速进行有效的限幅控制，即可实现位置速度的一体化设计，解决常规位置环二阶ADRC的速度不可控问题。

2.3速度限幅算法

当伺服系统开始工作时，电机应以最大限幅电流起动并加速运行。为有效地对电机运行的最高转速进行限幅控制，借鉴内置式PMSM的弱磁控制思想，当实际转速超过最高转速时，则用速度偏差信号作为反馈去削弱控制量的输出，构建一个速度控制环。引入速度限幅控制的位置环二阶ADRC的结构框图如图5所示，其中速度限幅的算法流程图如图6所示。图6中k(k>0)为速度偏差的比例控制系数，sgn为符号函数。

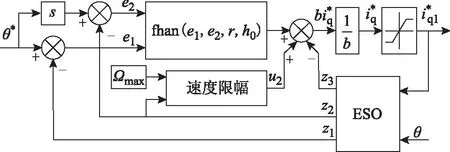
图5　引入速度限幅控制的位置环二阶ADRCFig.5　Modified ADRC controller by adding speed limitation

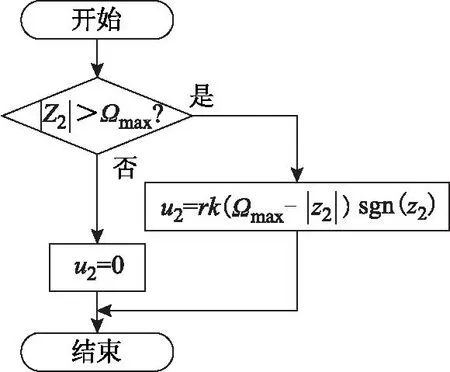
图6　速度限幅算法流程图Fig.6　Flow chat of the speed limitation algorithm

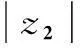
(14)

其中，转速反馈产生的控制量为

(15)

假设ESO对扰动的估计误差足够小，则将式(14)代入式(3)可得

(16)

由式(16)可知，稳态时电机的机械角加速度为零，电机恒速运行，实现了转速限幅。实际转速为

(17)

由式(17)可知，k取值过大，则实际转速与允许的最高转速之间的偏差很小，很容易引起转速在最高转速附近反复振荡；k取值过小，则会使实际转速与允许的最高转速之间的偏差过大，无法起到限幅的作用。采用PI控制器可解决此问题，但又会多一个控制量，且引入积分器可能存在积分饱和的问题，使算法变得复杂。由于对转速的控制精度要求不高，只要实现限幅即可，因此采用P控制，并合理设置比例控制系数k即可达到很好的控制效果。

图7为不同位置给定以及不同转速限幅下的位置定位及速度运行曲线。由图7可看出，当给定位置较小时，转速未达到限幅值，转速限幅不起作用；当给定位置较大时，系统在经历起动加速段后，进入速度限幅恒速段，随后进入减速段，并最终实现位置伺服系统的精确定位。

与常规的位置环二阶ADRC控制策略相比，本文所提出的位置速度一体化实现方案实现了四段式的位置伺服控制，从而解决了常规二阶ADRC中速度不可控的问题。而且在最高转速进行限幅的基础上，所提方法能够实现电机位置的最速定位，同时结构简单，便于数字实现，而且在不同的位置给定以及不同的转速限幅条件下均适用。

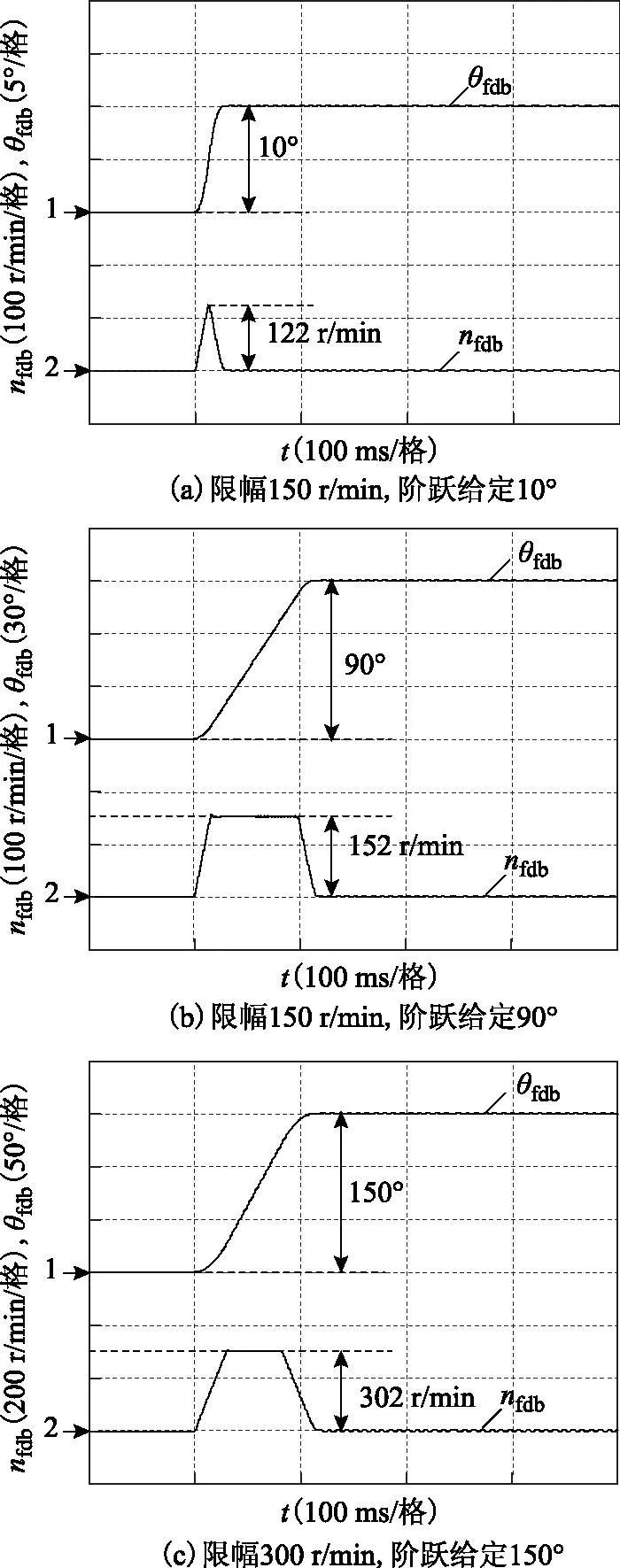
图7　有转速限幅且k=4.775时的位置响应Fig.7　Position response with speed limitationwhen k=4.775

3实验验证

本文对所提出的控制方案进行了实验验证。实验平台基于dSPACE实时仿真系统DS1103，硬件结构框图如图8所示。

分别取k为4.775(15/π，对应转速误差为2 r/min)和47.75，位置定位及速度运行曲线分别如图9和图10所示。

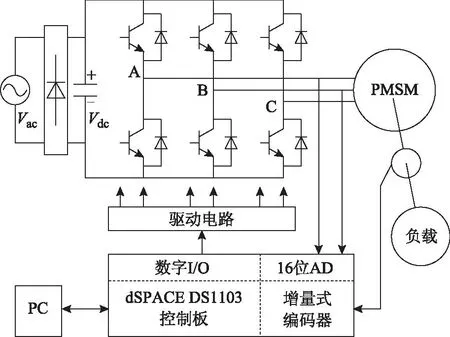
图8　系统硬件结构框图Fig.8　Block diagram of the system hardware

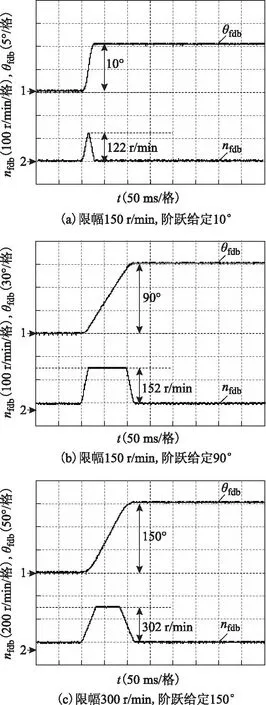
图9　k=4.775时的电机定位及速度响应曲线Fig.9　Position response and speed response when k=4.775

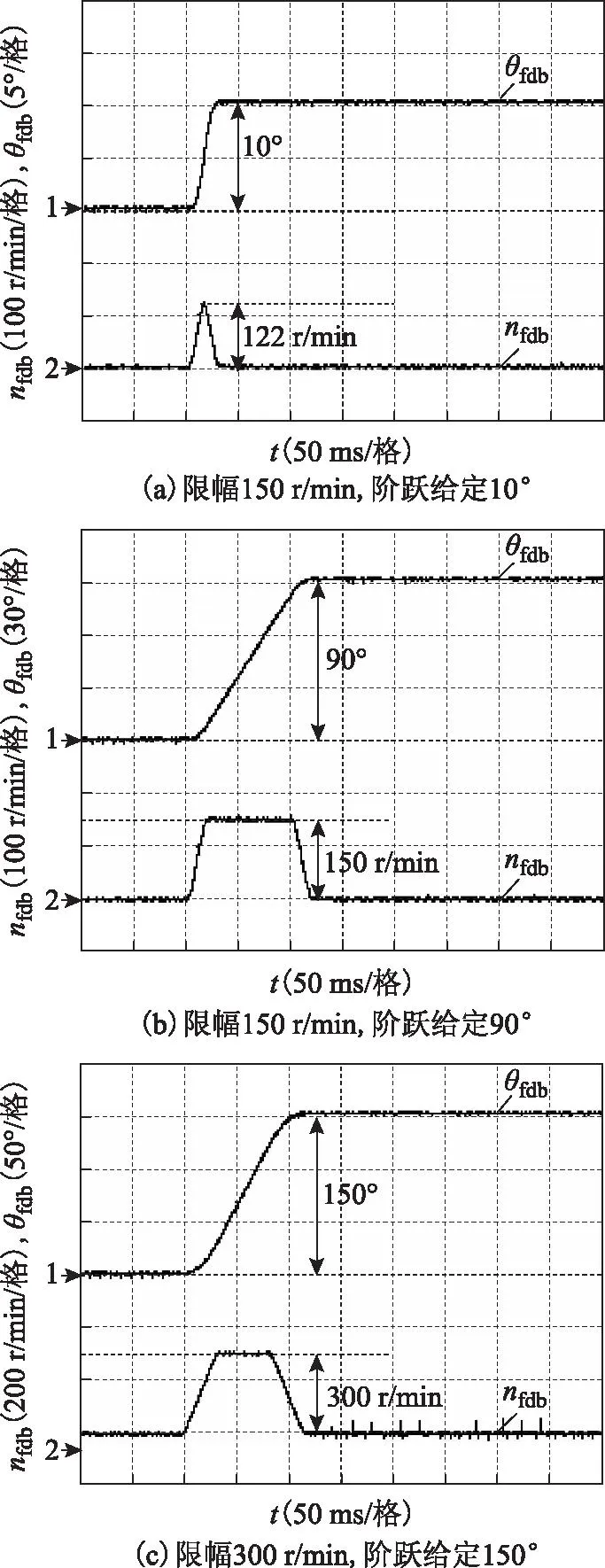
图10　k=47.75时电机定位及速度响应曲线Fig.10　Position response and speed response when k=47.75

图9a为给定位置较小时(10°)系统位置定位及速度响应曲线。系统定位过程中只经历加速、减速和低速趋近3个阶段便实现了最速定位。图9b为最高转速设置为150 r/min时的位置定位及速度响应曲线。给定位置为90°，伺服系统能够实现四段式位置定位，并且最高转速限制在152 r/min。图9c为最高转速设置为300 r/min时的位置定位及速度响应曲线。给定位置为150°，伺服系统能够实现四段式位置定位，并且最高转速限制在302 r/min。k取5时，三种位置给定下的最高转速应分别为122 r/min、150.2 r/min和300.2 r/min，图10中的实验结果与理论结果一致，验证了所提方法的有效性。不过，k=5时，限幅后的最高转速在设置值上下波动，导致电机在允许过程中存在噪音，而k=0.5时并无噪音。

图11为系统跟踪正弦位置给定时的动态响应。给定正弦位置信号幅值为20°，频率为5 Hz。可看出系统能够很好地跟踪连续变化的给定信号，位置跟踪误差为±0.06°，体现出良好的位置跟踪性能。

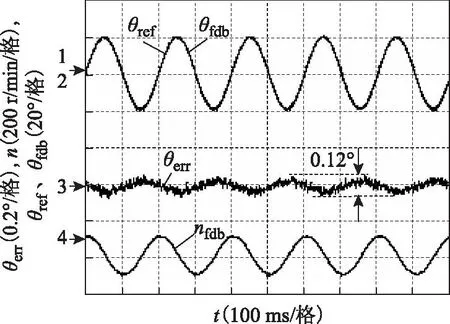
图11　跟踪正弦位置给定时的动态响应Fig.11　Dynamic response of tracking sine position reference

图12为系统加卸载时的位置误差和转矩电流波形。实验中，电机空载定位后，突加负载1.6 N·m，一段时间后再突卸至空载。加载过程通过Magtrol AHB-5型磁滞测功机实现。可看出当负载发生变化时，系统调节时间较短，体现出良好的抗扰性能，这同时也正是自抗扰控制系统的优势所在。

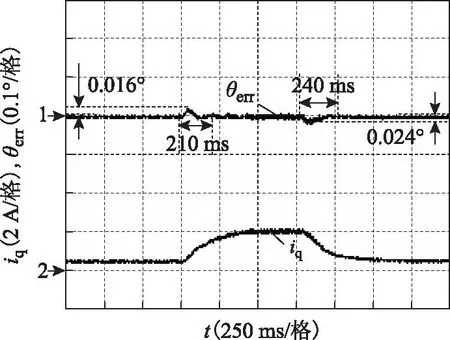
图12　加卸载时位置误差和转矩电流波形Fig.12　Position error and torque current curves

综上可以看出，本文所提出的转速控制方法对于不同的位置给定以及不同的转速限幅条件均适用，且对于自抗扰控制系统的跟踪性能和抗扰性能无影响。

4结论

本文针对位置环采用常规二阶自抗扰控制器的永磁同步电机伺服系统中速度不可控的问题，提出了一种位置速度一体化设计方法，其特点在于：

1)能够实现四段式的位置伺服控制，从而解决了常规二阶ADRC中速度不可控的问题。

2)在最高转速进行限幅的基础上，能够实现电机的最速位置定位。

3)对于不同的位置给定以及不同的转速限幅条件均适用。

4)同时具有良好的跟踪性能和抗扰性能。

综上所述，本文通过对常规位置环二阶自抗扰控制器进行改进，将位置、速度调节器综合设计为系统外环调节器，在保留自抗扰控制优点的基础上，解决了转速不可控的问题，进一步实现了伺服系统的精确定位，仿真和实验结果均验证了所提一体化设计方法的正确性和有效性。

参考文献

[1]黄科元，周滔滔，黄守道，等.永磁伺服系统基于微分自适应补偿的快速无超调控制策略[J].电工技术学报，2014，29(9)：137-144.

Huang Keyuan，Zhou Taotao，Huang Shoudao，et al.Non-overshoot and fast response control of PMSM servo system based on differential adaptive compensation[J].Transactions of China Electrotechnical Society，2014，29(9)：137-144.

[2]王江，王静，费向阳.永磁同步电动机的非线性PI速度控制[J].中国电机工程学报，2005，25(7)：125-130.

Wang Jiang，Wang Jing，Fei Xiangyang.Nonlinear PI speed control of permanent magnet synchronous motor[J].Proceedings of CSEE，2005，25(7)：125-130.

[3]梁骄雁，胡育文，鲁文其.永磁交流伺服系统的抗扰动自适应控制[J].电工技术学报，2011，26(10)：174-180.Liang Jiaoyan，Hu Yuwen，Lu Wenqi.Anti-disturbance adaptive control of permanent magnet AC servo system[J].Transactions of China Electrotechnical Society，2011，26(10)：174-180.

[4]Mohamed Y A I.Design and implementation of a robust current-control scheme for a PMSM vector drive with a simple adaptive disturbance observer[J].IEEE Transactions on Industrial Electronics，2007，54(4)：1981-1988.

[5]黄佳佳，周波，李丹，等.滑模控制永磁同步电动机位置伺服系统抖振[J].电工技术学报，2009，24(11)：41-47.

Huang Jiajia，Zhou Bo，Li Dan，et al.Sliding mode control for permanent magnet synchronous motor servo system[J].Transactions of China Electrotechnical Society，2009，24(11)：41-47.

[6]方斯琛，周波.滑模控制的永磁同步电机伺服系统一体化设计[J].中国电机工程学报，2009，29(3)：96-101.

Fang Sichen，Zhou Bo.Integrated design for permanent magnet synchronous motor servo systems based on sliding mode control[J].Proceedings of CSEE，2009，29(3)：96-101.

[7]胡金高，程国扬.鲁棒近似时间最优控制及其在电机伺服系统的应用.电工技术学报，2014，29(7)：163-172.

Hu Jingao，Cheng Guoyang.Robust proximate time-optimal control with application to a motor servo system[J].Transactions of China Electrotechnical Society，2014，29(7)：163-172.

[8]崔家瑞，李擎，张波，等.永磁同步电机变论域自适应模糊PID控制[J].中国电机工程学报，2013，33(增1)：190-194.

Cui Jiarui，Li Qing，Zhang Bo，et al.Permanent magnet synchronous motor of variable universe adaptive fuzzy PID control[J].Proceedings of CSEE，2013，33(S1)：190-194.

[9]Choi H H，Jung J.Discrete-time fuzzy speed regulator design for PM synchronous motor[J].IEEE Transactions on Industrial Electronics，2013，60(2)：600-607.

[10]韩京清.自抗扰控制器及其应用[J].控制与决策，1998，13(1)：19-23.

Han Jingqing.Auto-disturbances-rejection controller and its applications[J].Control and Decision，1998，13(1)：19-23.

[11]韩京清.自抗扰控制技术—估计补偿不确定因素的控制技术[M].北京：国防工业出版社，2008.

[12]Han Jingqing.From PID to active disturbance rejection control[J].IEEE Transactions on Industrial Electronics，2009，56(3)：900-906.

[13]Li S，Liu Z.Adaptive speed control for permanent-magnet synchronous motor system with variations of load inertia[J].IEEE Transactions on Industrial Electronics，2009，56(8)：3050-3059.

[14]卢达，赵光宙，曲轶龙，等.永磁同步电机无参数整定自抗扰控制器[J].电工技术学报，2013，28(3)：27-34.Lu Da，Zhao Guangzhou，Qu Yiliong，et al.Permanent magnet synchronous motor control system based on no manual tuned active disturbance rejection control[J].Transactions of China Electrotechnical Society，2013，28(3)：27-34.

[15]Su Y X，Zheng C H，Duan B Y.Automatic disturbances rejection controller for precise motion control of permanentmagnet synchronous motors[J].IEEE Transactions on Industrial Electronics，2005，52(3)：814-823.

[16]孙凯，许镇琳，盖廓，等.基于自抗扰控制器的永磁同步电机位置伺服系统[J].中国电机工程学报，2007，27(15)：43-46.

Sun Kai，Xu Zhenlin，Gai Kuo，et al.A novel position controller of PMSM servo system based on active-disturbance rejection controller[J].Proceedings of CSEE，2007，27(15)：43-46.

[17]滕福林，胡育文，李宏胜，等.基于自抗扰控制器的交流位置伺服系统[J].电气传动，2011，41(11)：46-50.

Teng Fulin，Hu Yuwen，Li Hongsheng，et al.AC position servo system based on active-disturbance rejection controller[J].Electric Drive，2011，41(11)：46-50.

[18]黄庆，黄守道，伍倩倩，等.基于模糊自抗扰控制器的永磁同步电动机伺服系统[J].电工技术学报，2013，28(9)：294-301.

Huang Qing，Huang Shoudao，Wu Qianqian，et al.PMSM servo system based on fuzzy active-disturbance rejection controller[J].Transactions of China Electrotechnical Society，2013，28(9)：294-301.

[19]Chou W D，Lin F J，Shyu K K.Incremental motion control of an induction motor servo drive via a genetic-algorithm-based sliding mode controller[J].Proceedings of Control Theory and Applications，2003，150(3)：209-220.

[20]Lai C K，Shyu K K.A novel motor drive design for incremental motion system via sliding-mode control method[J].IEEE Transactions on Industrial Electronics，2005，52(2)：499-507.

[21]许叙遥，林辉.基于动态滑模控制的永磁同步电机位置速度一体化设计[J].电工技术学报，2014，29(5)：77-83.

Xu Xuyao，Lin Hui.Integrated design for permanent magnet synchronous motor servo systems based on dynamic sliding mode control[J].Transactions of China Electrotechnical Society，2014，29(5)：77-83.

[22]袁东，马晓军，曾庆含，等.二阶系统线性自抗扰控制器频带特性与参数配置研究[J].控制理论与应用，2013，30(12)：1630-1640.

Yuan Dong，Ma Xiaojun，Zeng Qinghan，et al.Research on frequency-band characteristics and parameters configuration of linear active disturbance rejection control for second-order systems[J].Control Theory &Applications，2013，30(12)：1630-1640.

Integrated Design for Permanent Magnet Synchronous Motor Servo Systems Based on Active Disturbance Rejection Control

Zuo YuefeiZhang JieLiu ChuangZhang Tao

(College of Automation EngineeringNanjing University of Aeronautics and AstronauticsNanjing210016China)

AbstractIn order to solve the velocity control problem in the conventional second-order active disturbance rejection control(ADRC)for permanent magnet synchronous motor(PMSM)servo systems,a novel integrated design for position and speed loops is proposed.Firstly,the approach and problems of the conventional second-order ADRC are analyzed.Secondly,the velocity control is realized by using the novel integrated controller,which uses the idea of integrated design of the sliding mode control to realize the four-stage position control.The proposed method limits the highest speed through speed deviation feedback,and implements the fastest position orientation of the motor.The method is valid for various positions and speed limitations.The effectiveness of the proposed method is verified by both simulation and experimental results.

Keywords：Active disturbance rejection control(ADRC)，permanent magnet synchronous motor(PMSM)，position servo system，integrated design

收稿日期2015-03-04改稿日期2015-05-13

作者简介E-mail：zuo@nuaa.edu.cn(通信作者) E-mail：zhangjie1990@nuaa.edu.cn

中图分类号：TM351

国家自然科学基金(51377076)、江苏省“六大人才高峰”项目(YPC13013)和江苏省产学研资金项目(BY2014003-09)资助。

左月飞男，1989年生，博士研究生，研究方向为永磁同步电机伺服系统控制。

张捷男，1990年生，硕士研究生，研究方向为永磁同步电机伺服系统控制。