关于一类特殊的(α,β)度量的Landsberg曲率

许　飞， 曹贻鹏， 王素云

(装甲兵工程学院基础部, 北京 100072)

关于一类特殊的(α,β)度量的Landsberg曲率

许飞， 曹贻鹏， 王素云

(装甲兵工程学院基础部, 北京 100072)

摘要：在已构造的具有F=(α+β)2/α形式且含5个参量的(α,β)度量的基础上，研究了其射影平坦的条件及S曲率，并进一步计算了该种度量的Landsberg曲率，其曲率结果为后续研究曲率间关系奠定了基础。

关键词：Finsler度量； 射影平坦； (α,β)度量； Landsberg曲率

Finsler几何是在其度量上无二次限制的Riemann几何，自20世纪90年代以来，关于Finsler几何的研究有了很大的发展，尤其是对射影平坦的Finsler度量的性质及曲率形式作了较为系统的研究[1]。作为Finsler几何的一个重要研究方向，(α,β)度量的研究也取得了长足的进步，并构造出了各种形式的射影平坦的(α,β)度量[1-2]，得到了一些好的性质和曲率结果。在此背景下，笔者在已构造的射影平坦的(α,β)度量[3]的基础上，进一步计算了该种(α,β)度量的Landsberg曲率。

1概述

Finsler 度量中特殊而重要的一类度量是(α,β)度量[4]，它是由Riemannn度量α、1-形式β以及光滑流形M上函数φ组成，具体形式为 F=αφ(β/α)。例如：F=α+β，F=(α+β)2/2，F=α2/(α-β)等都是(α,β)度量。

Shen[5]构造了一类局部射影平坦、具有零旗曲率的(α,β)度量，形式如下：

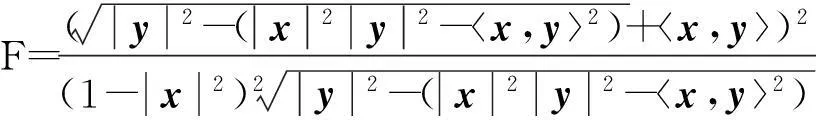
(1)

式中： y∈TxBn=Rn，TxBn表示Bn在x点的切空间，其可以具体地看作具有F=(α+β)2/2形式的(α,β)度量，其中，

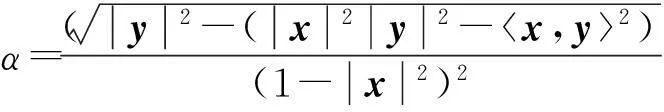
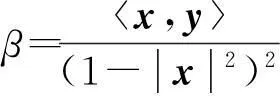
杨春红等[2]构造了一个具有3个参数、射影平坦 、具有零旗曲率的(α,β)度量，形式如下：

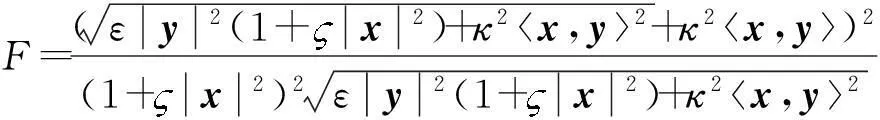
(2)

式中：y∈TxBn=Rn，其也可以具体地看作具有F=(α+β)2/2形式的(α,β)度量，其中，

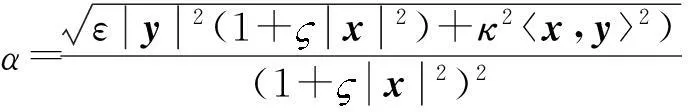
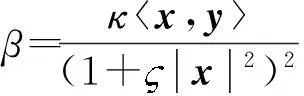
可见：式(2)是式(1)的推广。

笔者[3]曾进一步推广了式(2)，构造了一个具有5个参数的(α,β) 度量，形式如下：

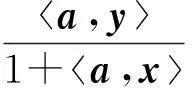
(3)

式中：y∈TxBn=Rn，其也可以具体地看作具有F=α+β形式的(α,β)度量，其中，

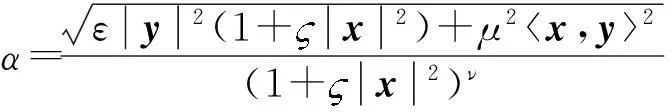
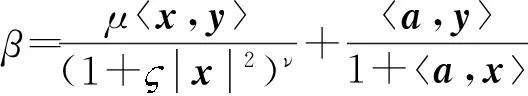
可见：式(3)又是式(2)的推广。在此基础上，笔者得到了该种(α,β)度量摄影平坦的条件。

定理1[3]：设F=α+β为定义在Rn的开子集Ω上的Finsler度量，其中α为Riemann度量，β为1-形式，

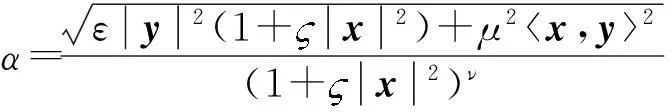
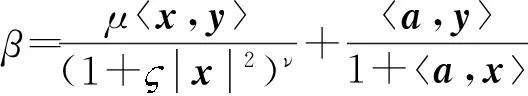
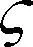
笔者[3]曾进一步对该种具有5个参数的(α,β)度量计算了其S曲率，得到了较为规整的形式，并在理论中具有良好的应用。

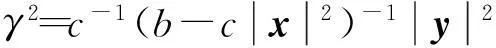
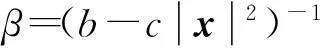
在本文中，笔者将进一步研究得到该种形式的(α,β)度量的Landsberg曲率。

2预备知识

定义1[6]： 光滑流形M上的Finsler 度量就是TM上的一个函数F:TM→[0,+∞)，满足：

1) 正则性，F在TM{0}上光滑；

2) 一阶正齐次性，F(x,λy)=λF(x,y)，∀λ>0；

则称F是流形M上的Finsler 度量，赋予Finsler 度量F的光滑流形M称为Finsler 流形。

如果Rn中一个开集U上的Finsler度量F在U上的测地线全是直线，即测地线σ(t)全是常向量，则称度量F是射影平坦[5]的，其有如下2个射影平坦的等价条件:

1)F在U上的测地线全是直线。

2)F测地系数具有以下形式：

Gi(y)=p(y)yi。

式中：

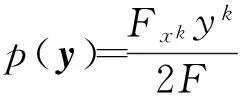
F满足

Fxkyiyk=Fxi。

定义2[7]：n维Finsler流形(M,F)上的Landsberg曲率定义为

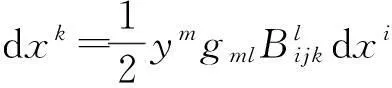
定义3[8]： 设(V,F)是Minkowski空间，对∀0≠y∈V，定义Cy:V×V×V→R上的多线性形式为

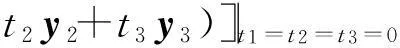
其中v1,v2,v3∈V，则称Cy为Cartan形式， C=Cy|y∈V{0},为Cartan挠率。

根据定义，若{ei}是V的一组基且

Cijk(y)=Cy(ei,ej,ek)，

则

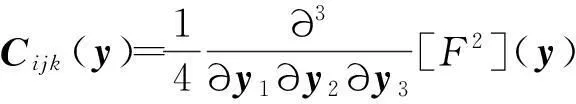
显然，Cy对称且是奇性的。

定义4[9]：流形(M,F)上的Spray是TM上的一个向量场，它在局部坐标系(xi,yi)下的形式如下：

其中Spray系数Gi(x,y)是TM{0}上的光滑函数，满足Gi(x,λy)=Gi(x,y)且

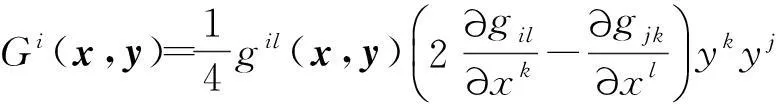
3Landsberg曲率的计算

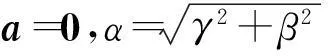
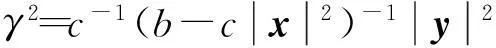
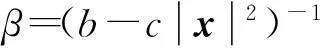
则其Landsberg曲率为

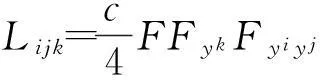
证明： 由于该度量是射影平坦的，Spray系数为

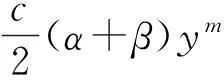
同理,

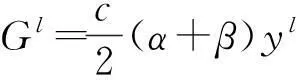
则

Gl(FyiylFyjyk+FyjylFyiyk+FykylFyiyj)=0。

对于如F=α+β形式的Randers度量，其Cartan形式为

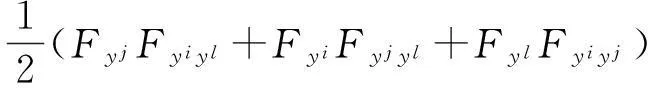
则

同理可得

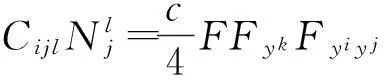
由于

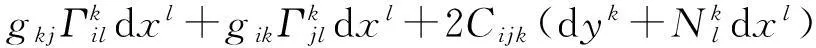
(4)

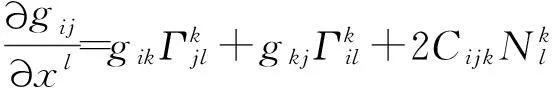
易知

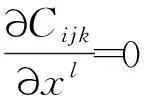
则

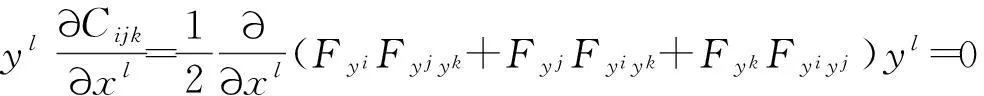
将上述结果代入Landsberg曲率公式

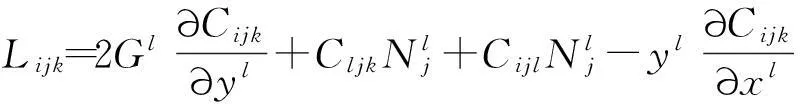
可得

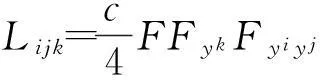
可见所构造的此类度量具有常Landsberg曲率，这在微分几何的理论和应用中具有重要的作用，为后续研究此类度量的性态奠定了基础。

参考文献：

[1]程新跃， 李海霞. 一类共形平坦的(α, β)-度量的研究[J]. 重庆理工大学学报(自然科学), 2014, 28(1): 112-119.

[2]杨春红, 莫小欢. 射影平坦的(α, β)度量的构造[J]. 内蒙古大学学报(自然科学版), 2006, 37(6): 610-614.

[3]许飞, 易良海, 黄依林, 等. 关于一类特殊的(α, β)度量的S曲率[J]. 装甲兵工程学院学报, 2012, 26(4): 100-102.

[4]沈一兵, 赵俐俐. 某些射影平坦的(α, β)度量[J]. 中国科学, 2006, 36(3): 248-261.

[5]ShenZM.ProjectivlyFlatFinslerMetricsofConstantFlagCurvature[J].TransofAmerMarhSoc, 2003, 355(4): 1713-1728.

[6]黎芳, 王佳. 共形且射影相关的Finsler空间[J]. 西南师范大学学报(自然科学版)， 2005, 30(3): 405-408.

[7]许飞, 张迪, 王素云. 流行及其子流形的两类曲率关系[J]. 装甲兵工程学院学报, 2011, 25(3): 100-102.

[8]TianHJ.OntwoClassesof(α, β)-metricwithBoundedCartanTorsion[J].AdvancesinMathematics, 2015, 44(2): 287-297.

[9]邓义华. 一类射影平坦的多项式(α, β)度量[J]. 数学学报, 2007, 50(6): 1365-1367.

(责任编辑: 尚彩娟)

Landsberg Curvature about a Class of Special (α,β)-metrics

XU Fei, CAO Yi-peng, WANG Su-yun

( Department of Fundamental Courses, Academy of Armored Force Engineering, Beijing 100072, China)

Abstract：On the basis of a class of (α,β)-metrics with form of F=(α+β)2/α and five parameters, the projectively flat condition and S curvature are studied, and the Landsberg curvature of (α,β)-metrics is furthermore calculated. The curvature result lays foundation for research on the relations between curvatures.

Key words:Finsler metrics; projectively flat; (α,β)-metrics; Landsberg curvature

文章编号：1672-1497(2016)02-0108-03

收稿日期：2015-09-11

作者简介：许飞(1981-)，男，讲师，硕士。

中图分类号：O186

文献标志码：A

DOI：10.3969/j.issn.1672-1497.2016.02.022