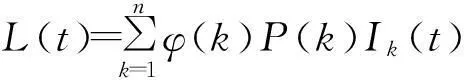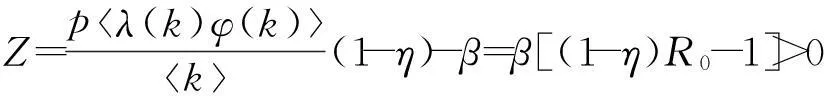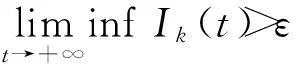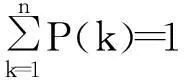无标度网络上具有时滞的SIRS谣言传播模型

李　涛

(军械工程学院基础部， 河北 石家庄 050003)

无标度网络上具有时滞的SIRS谣言传播模型

李涛

(军械工程学院基础部， 河北 石家庄 050003)

摘要：通过分析具有遗忘效应的谣言传播特点和方式，在无标度网络环境下建立了一类具有时滞的SIRS谣言传播模型,计算了传播过程中的基本再生数，并通过证明得到结论:当基本再生数小于1时，谣言将逐渐消失；当基本再生数大于1时，谣言将持续存在。最后，通过数值仿真验证了所得结论的正确性。

关键词：无标度网络； SIRS谣言； 时滞； 基本再生数

近年来，随着网络技术的发展，谣言这一古老的传播学现象以前所未有的速度疯狂传播，造成了严重的危害[1]。因此，如何有效地监控与治理谣言的传播已成为信息时代一个亟待解决的问题。人们发现网络谣言和传染病作为有害传播源，具有很多类似的传播机理，经典的网络谣言传播模型延续了传染病传播模型的建模思想和分析方法[2]，它把用户的状态分为无知者、传播者和免疫者3类，通过建立三者之间的状态转移关系，得到微分动力学模型[3-4]。但是，这些模型均未考虑社会网络的拓扑结构对谣言传播的影响。而复杂网络理论研究表明：作为谣言传播载体的社会网络、信息网络等都具有无标度特性[5]。目前，大部分的研究[6-9]均为常微分方程模型，基于无标度网络并考虑时滞因素的数学模型非常少。由于谣言的传播具有非常强的时效性，因此建立具有时滞因素的谣言传播模型，无疑能更好地描述谣言传播过程。为此，笔者将互联网视为无标度网络，针对实际个体谣言传播能力有限的情况考虑了具有饱和性质的非线性传播率，建立了一类具有时滞的SIRS谣言传播模型，通过计算得到了谣言传播的基本再生数，并对模型的平衡点以及时滞对谣言传播的影响进行研究，最后通过数值仿真进行验证。

1模型建立

根据现实网络世界谣言传播的特点，网络中的个体可分为无知者、传播者和免疫者3类：1)无知者(Susceptible)是指从未听到过谣言的人，但通过和谣言传播源的接触，其变成潜在传播者的概率为λ(k)，潜在传播者开始传播谣言的概率为p；2)传播者(Infective)是指相信并开始传播谣言者，传播者也可能以各种渠道得知正确信息后不再传播谣言而以概率β转化为免疫者；3)免疫者(Removed)是指确信谣言为假的群体，免疫者也在经过时间τ后，由于网络中大量信息的存在或对谣言不感兴趣等因素，从而遗忘之前的谣言而成为无知者。令Sk(t)、Ik(t)、Rk(t)分别表示t时刻在度值为k(k=1,2,…,n)的节点中无知者、传播者、免疫者所占的比例。设所有参数均为正常数，根据平均场理论，建立如下传播动力学方程：

(1)

式中：λ(k)为感染率，与节点的度值k有关[10];

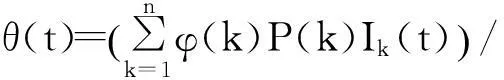
(2)

为任意一条边指向传播节点的概率，其中，P(k)为度值为k的节点占所有节点的比例，kkP(k)，为节点平均度值，非线性函数φ(k)=akα/(1+bkα),a>0,0≤α≤1,b≥0，为度值为k的节点的有效接触率[11]，φ(k)具有饱和性，即φ(k)=a/b,b≠0，因此它可以较准确地描述单位时间内单个谣言传播者传播能力有限的情况。由于Sk(t)+Ik(t)+Rk(t)=1，于是系统(1)等价于如下系统：

(3)

2模型分析

定理1：令R0=pλ(k)φ(k)/(βk)，当R0<1时，系统(3)存在平衡点E0(1,1,…,1,0,0,…,0)；当R0>1时，系统(3)存在平衡点。

(4)

式中：

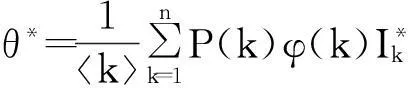
(5)

解方程组(4)可得

(6)

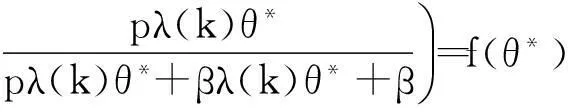
(7)

显然θ*=0是方程(7)的解，此时系统(3)有唯一的平衡点E0。若当方程(7)有非零解时，注意到

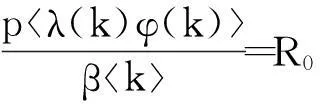
且

此时，y=f(θ)与y=θ在第一象限内有唯一交点。因此，方程(7)有唯一的正解，根据式(6)可得此时系统(3)有平衡点E*。

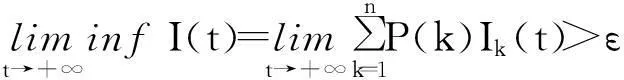
证明： 1) 当R0<1时，在{(S1,S2,…,Sn,I1,I2,…,In):Sk,Ik≥0,Sk+Ik≤1,k=1,2,…,n}，t≥0上考虑Lyapunov函数

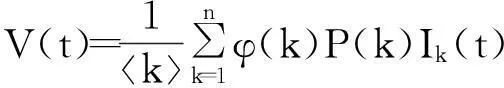
计算V(t)沿系统(3)的导数可得

注意到θ(t)≥0且R0<1，即pλ(k)φ(k)/(βk)<1，可得pλ(k)φ(k)/k-β<0，因此可以推出V′(t)≤0，并且当且仅当θ(t)=0时，即Ik(t)=0时有V′(t)=0。由LaSalle不变原理可得：当R0<1时，平衡点E0全局渐近稳定。

设ρ为特征方程的特征值，此时平衡点E0的Jacobian矩阵为

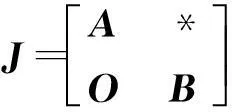
式中：O为n阶零矩阵；A为n阶对角阵，

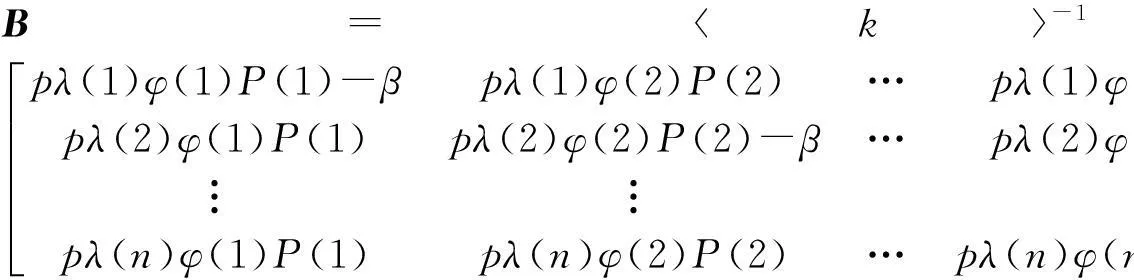
将矩阵J第m列乘以λ(m)/λ(1)加到第n+1列，m=n+2,n+3,…,2n，将第n+1行乘以-λ(m)/λ(1)加到第n+m行，m=2,3,…,n，可得

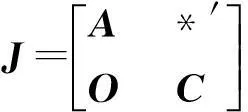
式中：

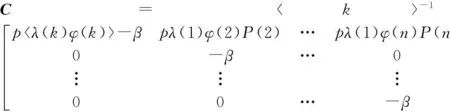
对应的特征方程为

λ(k)φ(k)+β)=0,

显然ρ=-e-ρτ与ρ=-β是特征根，其他特征根满足

ρ=pk-1λ(k)φ(k)-β，

当R0>1时，令

F(ρ)=ρ-pλ(k)φ(k)/k+β，

那么

F(0)=-pλ(k)φ(k)/k+β<0，

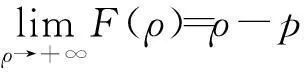
由零点定理可知：函数F(ρ)在(0,+∞)至少存在一个根ρ0，即系统(3)的特征方程至少存在一个正实根，因此当R0>1时，平衡点E0不稳定。

记

D={(S1,S2,…,Sn,I1,I2,…,In):Sk,Ik≥0,Sk+

Ik≤1,k=1,2,…,n}，

D0={(S1,S2,…,Sn,I1,I2,…,In)∈D:

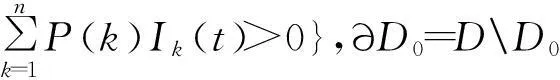
显然D0是系统(3)的正向不变集。系统(3)为耗散系统，E0为系统(3)在∂D0上唯一的平衡点，且系统(3)在∂D0上的Ω极限集为E0，E0孤立且非循环。

最后只需要证明Ws(E0)∩D0=∅，Ws(E0)为E0的稳定流形。这里采取反证法证明，假设其非真，则D0内存在一个解(S1(t),S2(t),…,Sn(t),I1(t),I2(t),…,In(t))，当t→+∞时，有Sk(t)→1,Ik(t)→0。

由于R0>1，可取0<η<1,使得(1-η)R0>1。且存在一个T>0，使得对于所有的t≥T和k=1,2,…,n，有1-η

显然L(t)是有界函数，但L(t)沿系统(3)的导数为

Ik(t)=ZL(t)。

式中:

由定理2可知：系统(3)的基本再生数为R0=pλ(k)φ(k)/(βk)，当R0<1时，无病平衡点全局渐近稳定，此时谣言将消失；当R0>1时，无病平衡点不稳定，由于infI(t)>ε，此时谣言将持续存在。

3数值仿真

当λ=0.2，p=0.2，β=0.2时，R0=0.642 9<1，系统(1)中k=10,30,80的节点中传播者节点的比例I10、I30、I80随时间t的变化趋势如图1所示。可以看出:当R0<1时,网络中的谣言将逐渐消失。

图1　R0<1时系统(1)中I10、I30、I80随t的变化趋势

图2　R0>1时系统(1)中I10、I30、I80随t的变化趋势

当λ=0.2，p=0.2，β=0.02时，R0=3.214 7>1， I10、I30、I80随t的变化趋势如图2所示。可以看出：当R0>1时,谣言在网络中将持续存在。

参考文献：

[1]李国武. 谣言实现的社会机制及对信息的治理[J]. 社会, 2005, 242(4): 1-2.

[2]马知恩, 周义仓, 王稳地, 等. 传染病动力学的数学建模与研究[M]. 北京: 科学出版社, 2004: 11-15.

[3]Daley D J, Kendall D G. Stochastic Rumors[J]. IMA Journal of Applied Mathematics, 1965, 1(1): 42-55.

[4]Maki D, Thomson M. Mathematical Models and Applications[M]. Englewood Cliffs: Prentice-Hall, 1973.

[5]汪小帆, 李翔, 陈关荣. 网络科学导论[M]. 北京: 高等教育出版社, 2012: 21-26.

[6]Sudbury A. The Proportion of Population Never Hearing a Rumor[J]. Journal of Applied Probability, 1985, 22(2): 443-446.

[7]Moreno Y, Nekovee M, Pacheco A. Dynamics of Rumor Spreading in Complex Networks[J]. Physical Review E, 2004, 69(6): 1-8.

[8]顾亦然, 沈贤. 无标度网络中谣言传播的研究 [J]. 计算机技术与发展, 2013, 23(8): 254-257.

[9]Isham V, Harden S, Nekovee M. Stochastic Epidemics and Rumors on Finite Random Networks[J]. Physica A, 2010, 389(3): 561-576.

[10]Zhu G, Fu X, Chen G. Global Attractively of a Network-based Epidemic SIS Model with Nonlinear Infectivity[J]. Communication in Nonlinear Science and Numerical Simulation, 2012, 17(6): 2588-2594.

[11]Zhang H, Fu X. Spreading of Epidemics on Scale-free Networks with Nonlinear Infectivity[J]. Nonlinear Analysis, 2009, 70(9): 3273-3278.

[12]Thieme H R. Persistence under Relaxed Point-dissipativity (with Application to an Endemic Model) [J]. SIAM Journal on Mathematical Analysis, 1993, 24(2): 407-435.

(责任编辑: 尚彩娟)

SIRS Rumors Spreading Model with Time Delay on Scale-free Network

LI Tao

(Department of Fundamental Courses, Ordnance Engineering College, Shijiazhuang 050003, China)

Abstract：By analyzing the characteristics and the way of spreading rumors with forgetting effect, a novel SIRS rumors spreading model with time delay on scale-free network is proposed. The basic reproductive number for the model is calculated. it is concluded through verification that the rumors will die out when the basic reproductive number is less than 1, while the persistence of the rumors is shown when the basic reproductive number is larger than 1. At last, numerical simulations are given to illustrate the effectiveness of the analytical results.

Key words:scale-free network; SIRS rumor; time delay; basic reproductive number

文章编号：1672-1497(2016)02-0104-04

收稿日期：2015-11-23

作者简介：李涛(1983-)，男，硕士研究生。

中图分类号：G206

文献标志码：A

DOI：10.3969/j.issn.1672-1497.2016.02.021