基于ELMD能量矩的坦克变速箱特征提取方法

李慧梅， 封会娟， 安　钢, 王　硕

(1. 军事交通学院军用车辆系， 天津 300161； 2. 装甲兵工程学院机械工程系， 北京 100072; 3. 95900部队, 河南 开封 47500)

基于ELMD能量矩的坦克变速箱特征提取方法

李慧梅1， 封会娟1， 安钢2, 王硕3

(1. 军事交通学院军用车辆系， 天津 300161； 2. 装甲兵工程学院机械工程系， 北京 100072; 3. 95900部队, 河南 开封 47500)

摘要：针对坦克变速箱故障时振动信号的复杂性和不确定性，提出了总体局部均值分解(Ensemble Local Mean Decomposition, ELMD)能量矩的故障特征提取方法，对坦克实车试验中测取的变速箱正常、主轴滚动轴承滚动体点蚀和3挡被动齿轮断齿3种状态下的振动信号进行计算。结果表明：该方法提取的特征能很好地反映变速箱的状态，从而实现对变速箱的故障诊断。

关键词：坦克变速箱； 特征提取； ELMD； 能量矩

变速箱作为坦克最重要的传动部件之一，工作时所承受的载荷变化剧烈，具有较高的故障率,因此对其进行状态监测和故障诊断具有重要意义。坦克变速箱发生故障时的振动信号十分复杂，影响因素较多，不确定性较强。若仅从时域或频域的角度提取信号特征来进行故障诊断，效果往往不理想。近年来，从时频域的角度分析信号取得了良好的故障诊断效果[1-2]。其中，小波变换、经验模式分解(Empirical Mode Decomposition，EMD)和局部均值分解(Local Mean Decomposition，LMD)等是变速箱常用的时频信号分析方法[3-5]。但这些方法在进行信号分析时还存在一些不足，如：小波变换在分析信号时基函数的选择不是自适应的；EMD方法存在端点效应、模态混叠、过包络和欠包络等问题；LMD方法存在最优滑动平均步长确定困难、模态混叠和计算量大等问题。为解决LMD方法的模态混叠问题，程军圣等[6]提出了基于噪声辅助分析的总体局部均值分解(Ensemble Local Mean Decomposition，ELMD)方法。ELMD方法能自动地将信号分解到由白噪声所确定的滤波器组的各个通频带中，从而有效地减轻了模态混叠现象。信号经ELMD方法分解后，能得到反映原振动信号主要成分且物理意义明确的乘积函数(Product Function, PF)分量，适合处理变速箱箱体表面这种复杂振动信号。笔者针对变速箱发生故障时振动信号在各频段的能量将发生变化且随时间分布的特点，利用ELMD方法将信号分解到各频带上得到多个PF分量，然后各频带分量的能量矩作为特征向量来判断变速箱所处的状态，以期为变速箱的故障诊断提供一种有效的特征提取方法。

1ELMD方法

1.1LMD的模态混叠现象

信号经LMD分解后可表示为

(1)

式中：PFi(t)为分解得到的第i个PF分量；uk(t)为信号分解得到的残余分量。信号的LMD分解过程是完全自适应的，其具体计算步骤可参见文献[7]。

本文通过对仿真信号进行LMD分解来说明LMD的模态混叠现象。设仿真信号由1个正弦信号x1(t)和1个小幅值的间歇正弦信号x2(t)叠加而成，其中：t∈[0, 0.8]，采样频率为1 kHz。仿真信号的时域波形如图1所示。

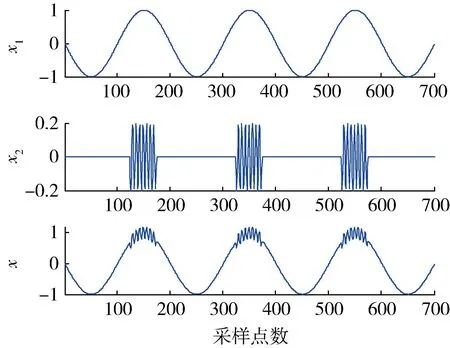
图1　仿真信号的时频波形

对仿真信号进行LMD分解，其结果如图2所示，可以看出：第1个分量同时包含了高频间歇正弦信号和低频正弦信号，且低频正弦信号被分解到第1、2个分量中，发生了模态混叠现象。模态混叠现象一般是由信号的间歇性所引起[8]，即由信号在时间尺度上的不连续造成的。在实际中，数据一般都包含有信号和噪声，因此LMD的模态混叠现象是普遍存在的。

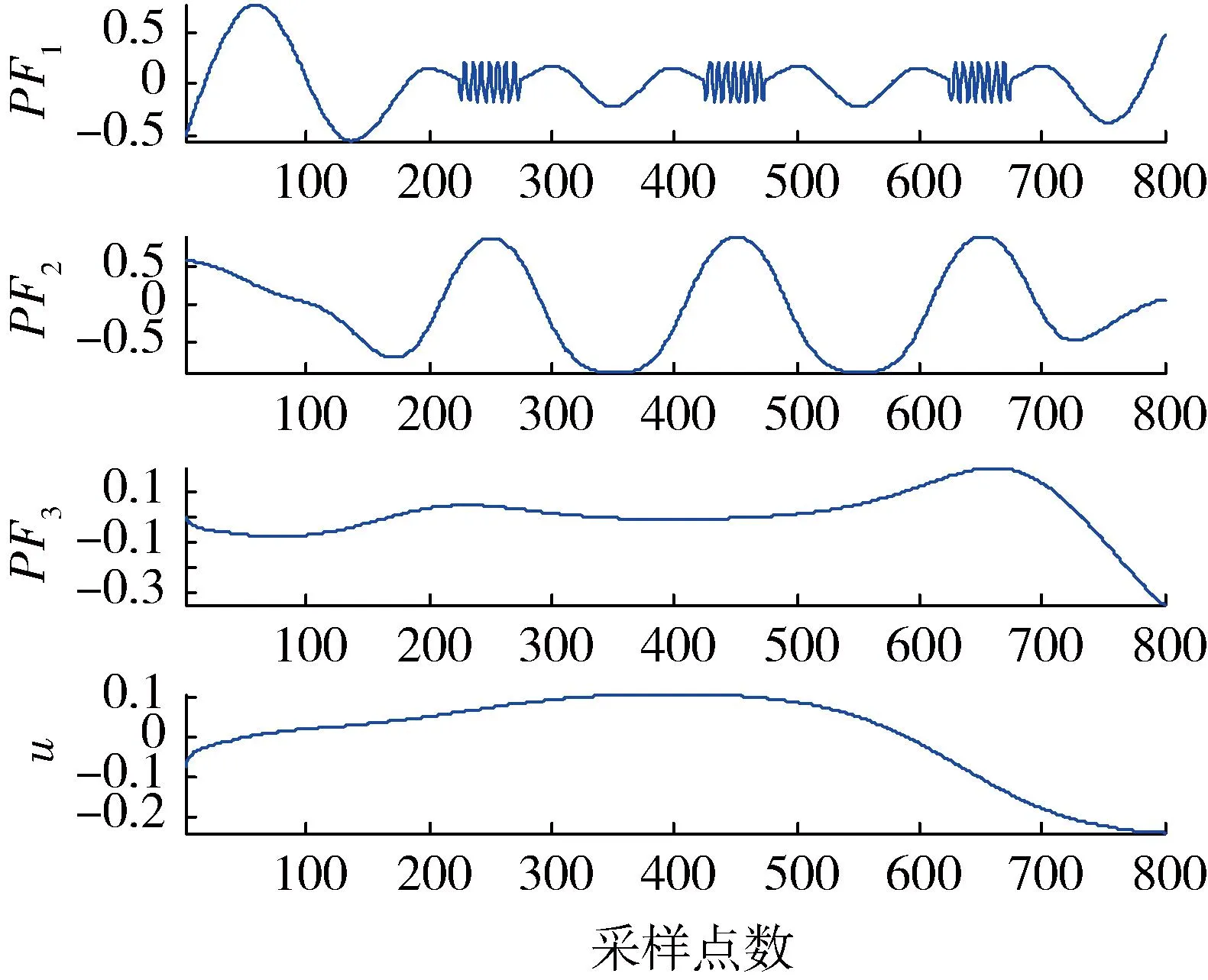
图2　仿真信号的LMD分解结果

1.2ELMD方法的基本原理[6]

ELMD方法是对LMD方法的改进，实质就是信号叠加了不同高斯白噪声后的多次LMD分解结果的平均值，其具体实现步骤如下：

1)确定LMD分解的总次数为M，加入白噪声信号的幅值比值系数为α。其中α的计算公式为

α=σ/σ0，

(2)

式中：σ为加入白噪声的幅值标准差；σ0为待分析信号x(t)的幅值标准差。

2) 对信号进行第k次LMD分解，k=1,2,…,K。待处理信号xk(t)为

xk(t)=x(t)+αnk(t)，

(3)

式中：nk(t)为一随机高斯白噪声。对xk(t)进行LMD分解，得到J个PF分量PFj,k(j=1,2,…,J)，PFj,k为第k次分解得到的第j个分量。

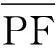
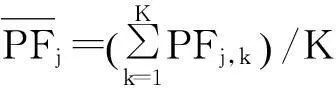
(4)

从ELMD方法的具体实现步骤中可以看出：ELMD方法首先给待分析信号加入高斯白噪声，然后再进行LMD分解。这样，在给信号加入高斯白噪声后,使得信号在不同尺度上均具有了连续性，从而有效地减轻了模态混叠现象。又由于一定数量的白噪声的均值近似为0，取多次LMD分解结果的均值作为最终结果可消去白噪声成分，获得真实结果。

1.3仿真分析

为验证ELMD方法的抗模态混叠能力，对图1中的仿真信号进行ELMD分解。分解时按照文献[9]给出的加入白噪声的准则确定α=0.03，M=100，其结果如图3所示。可以看出：高频间歇正弦信号和低频正弦信号被成功分开，模态混叠现象得到了有效抑制。

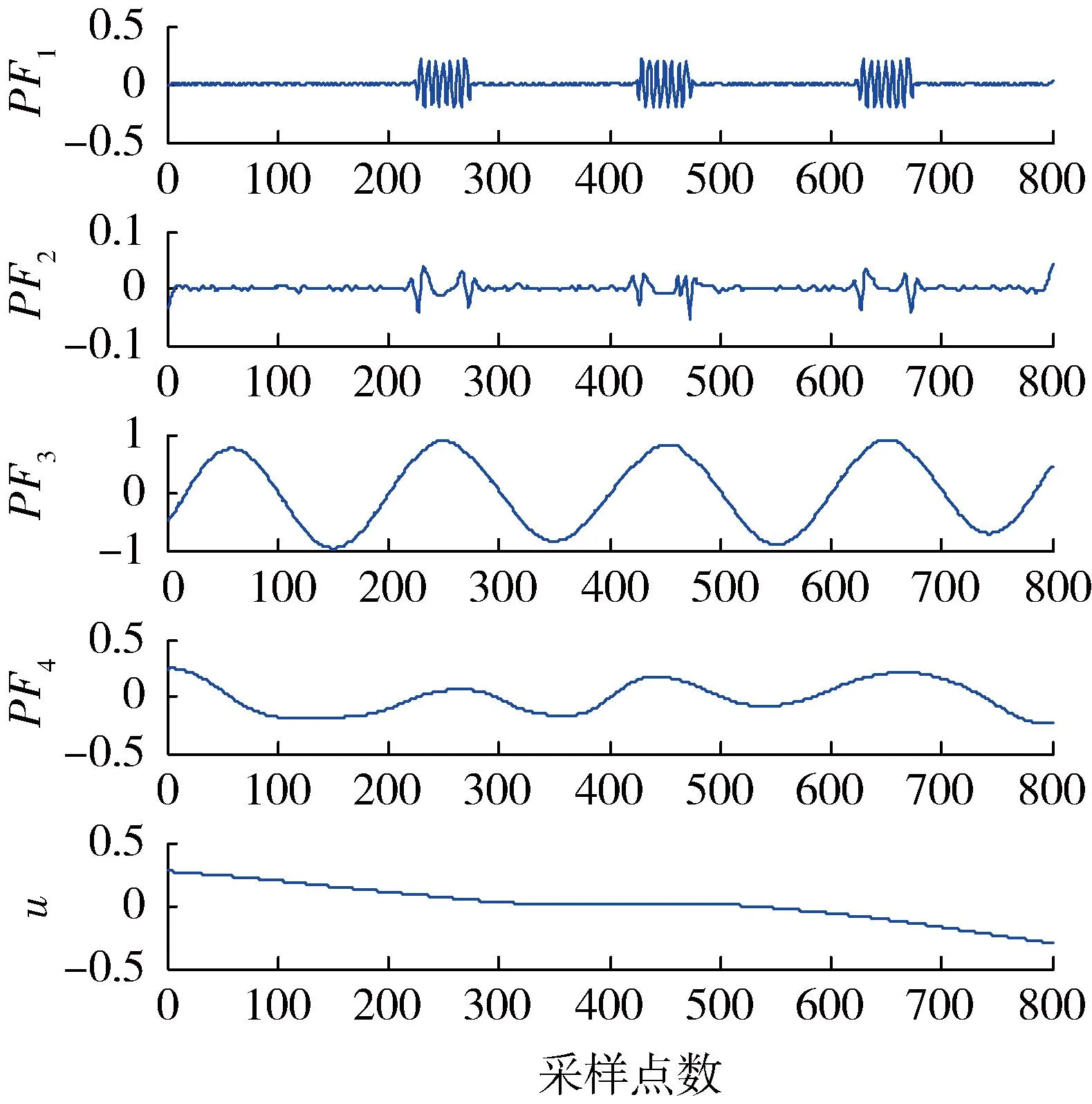
图3　仿真信号的ELMD分解结果

2基于ELMD能量矩的特征提取方法

ELMD方法分解得到多个PF分量，每一个PF分量具有相应的频带范围，包含着不同的故障信息。当机械设备处于不同状态时，各频带分量的能量将发生变化，综合考虑各分量能量值的变化情况，可区分设备的各种状态。但未考虑每个分量的能量随时间分布的特点，这样会损失一些故障信息，从而使该特征参数包含的信息量少，故障特征反映不够精确[10]。为了更好地挖掘隐藏在信号中的故障信息，可采用各分量的能量矩作为特征向量。对信号进行ELMD分解得到各PF分量，然后基于时间来计算各PF分量的能量特征，通过各PF分量能量矩的变化，可以实施有效的状态监测和故障诊断。

设信号x(n) (n=1,2,…,N)经ELMD分解得到m个PF分量PFi(n) (i=1,2,…,m)，参考IMF分量能量矩的定义方式[11]，定义PF分量的能量矩E(PFi)为

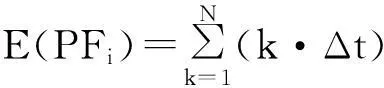
(5)

式中：Δt为采样周期；N为总的采样点数；k为采样点。

信号的总能量矩E(x(n))为

(6)

则归一化后的PF分量的能量矩Ei为

Ei=E(PFi)/E(x(n))。

(7)

从式(5)可以看出：PF分量的能量矩E(PFi)不仅考虑了PF分量的能量大小，而且还考虑了PF分量的能量随时间的分布情况。将归一化后的各个PF分量的能量矩组成的向量E=(E1,E2,…,Em)作为特征向量，对其故障状态进行判别。PF分量能量矩向量的提取过程如下：

1) 利用ELMD方法分解原始振动信号，得到m个PF分量PFi(n)；

2) 按式(5)计算各PF分量的能量矩E(PFi)；

3) 为便于数据的分析与处理，按式(7)进行归一化处理，得到归一化后的能量矩Ei；

4) 构造以各PF分量的能量矩为元素的向量E=(E1,E2,…,Em)作为变速箱状态识别的特征向量，对其进行状态判别。

3坦克变速箱特征提取实例

考虑到试验的可操作性和安全性，本文模拟了变速箱正常、变速箱主轴7216滚动轴承滚动体点蚀和3挡被动齿轮断齿3种状态下的振动信号。

试验时，坦克挂3挡，发动机转速为1 000 r/min，原地断履带运转，其传感器在变速箱上的安装位置如图4所示。图5为3种状态下变速箱振动信号的时域波形。利用上述特征提取方法计算图5所示的振动信号的PF分量能量矩。首先，对振动信号进行ELMD分解。为了使各个样本的PF分量的能量矩具有可比性，根据分解得到的信号特点，人为地限制每个样本分解得到7个PF分量后停止运算，余项记为第8个分量。图6为图5所示的振动信号的ELMD分解结果。然后，根据式(8)计算3种状态下变速箱振动信号的PF分量的能量矩，其结果如图7所示。可以看出变速箱3种状态下振动信号的PF分量的能量分布存在明显的差异：1)当变速箱正常

图4　传感器在变速箱上的安装位置

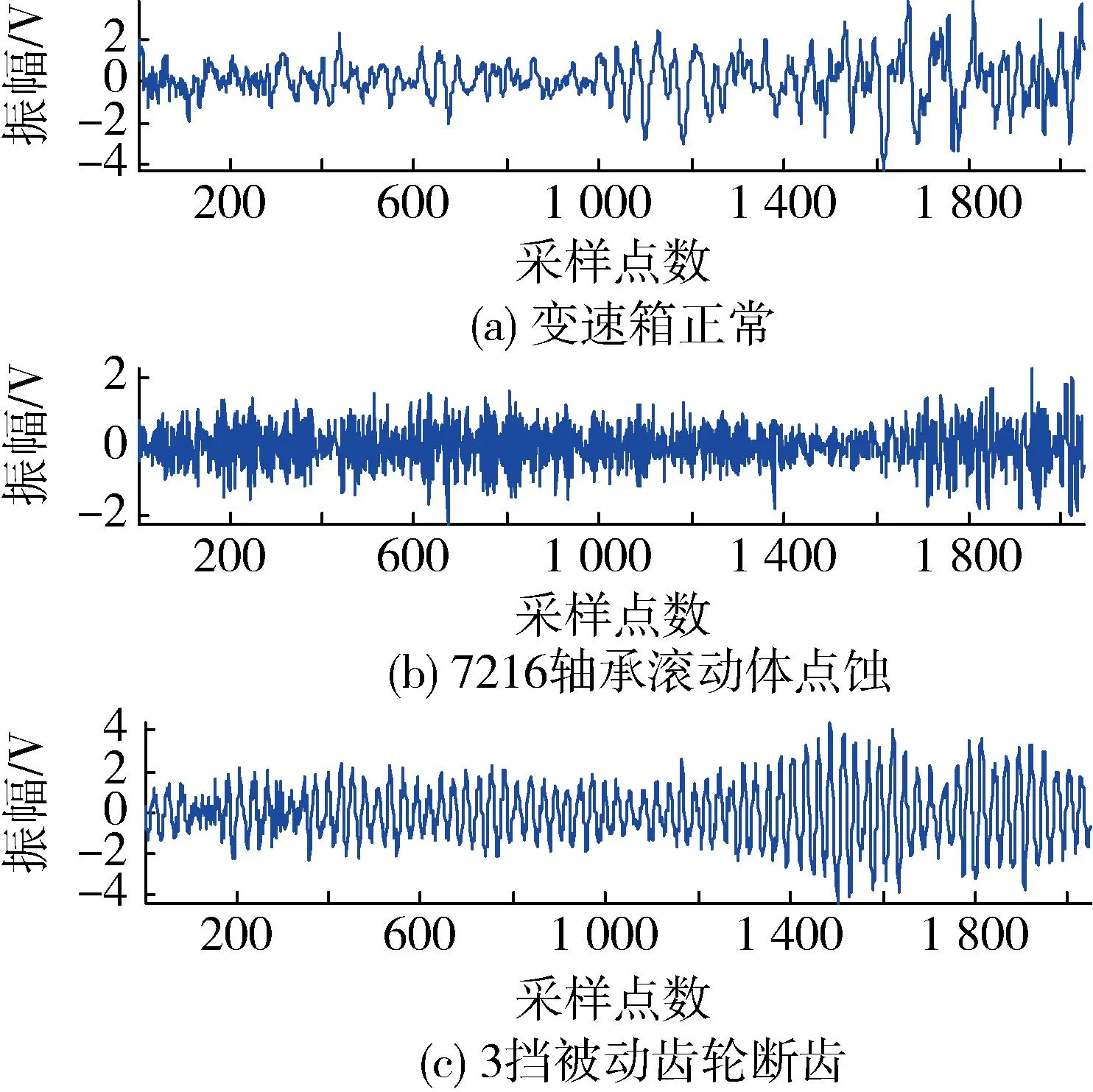
图5　3种状态下变速箱振动信号的时域波形

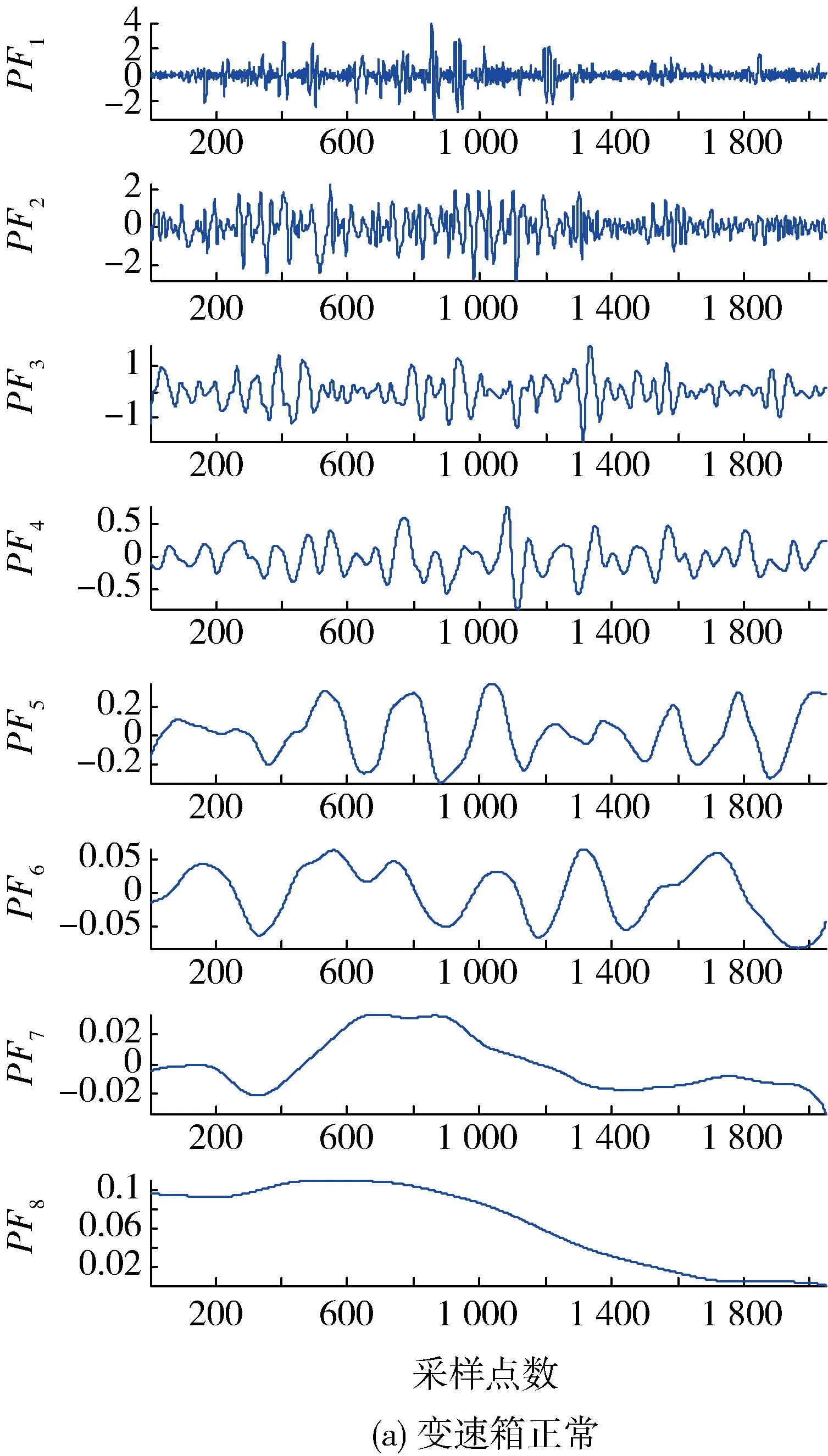
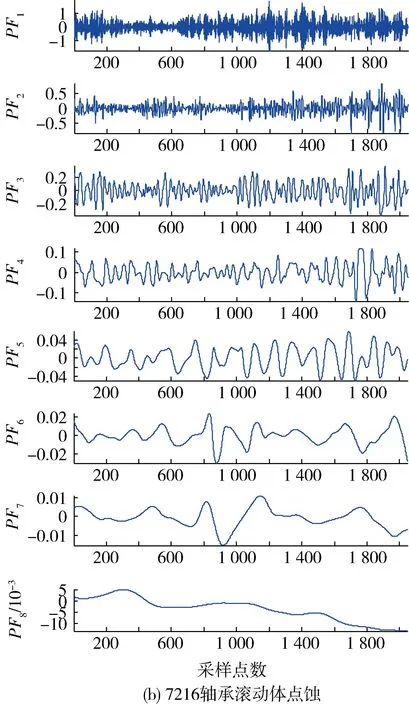
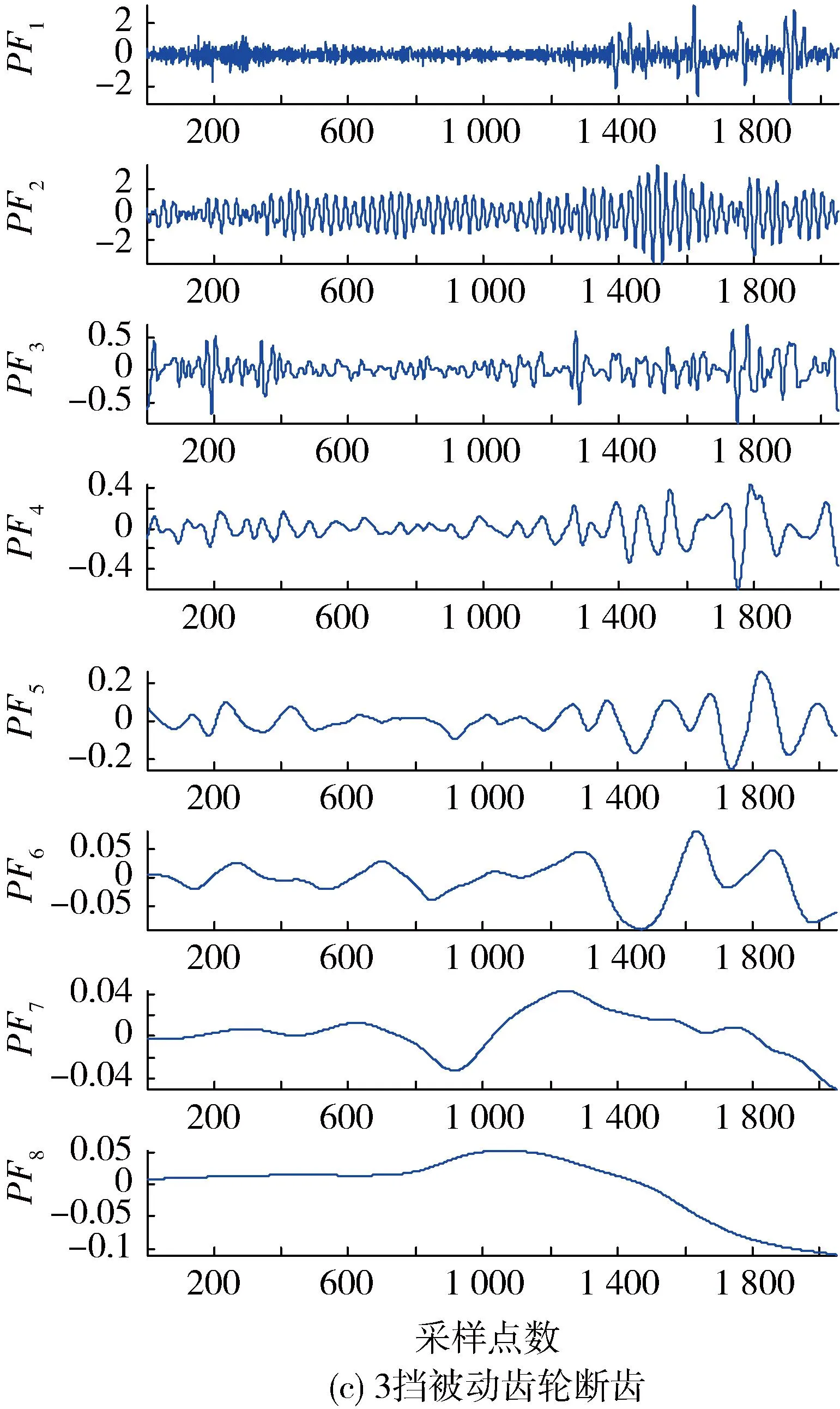
图6　3种状态下变速箱振动信号的ELMD分解结果

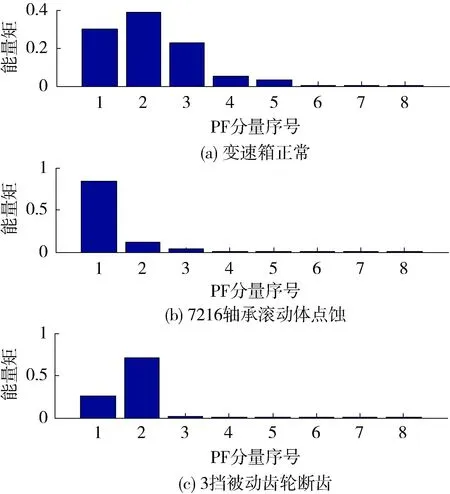
图7　3种状态下变速箱振动信号的PF分量能量矩

状态时，能量主要集中在前3个PF分量；2)当7216轴承滚动体点蚀故障时，能量主要集中在第1个PF分量；3)当3挡被动齿轮断齿故障时，能量主要集中在前2个PF分量，且第1个PF分量和第2个PF分量的能量相差较多；4)同种状态下各个样本的能量矩分布相似。因此，可以通过能量矩的分布情况，将变速箱的各种状态区分开来，从而实现变速箱的故障监测和诊断。

参考文献：

[1]孙海亮， 訾艳阳， 袁静， 等. 非抽样多小波和Hilbert-Huang时频分析在行星减速器早期故障诊断中的应用[J]. 机械工程学报， 2013， 49(3)： 56-62.

[2]王书涛， 李亮， 张淑清， 等. 基于EEMD样本熵和GK模糊聚类的机械故障识别[J]. 中国机械工程， 2013， 24(22)： 3036-3040.[3]罗毅， 甄立敬. 基于小波包与倒频谱分析的风电机组齿轮箱齿轮裂纹诊断方法[J]. 振动与冲击， 2015， 34(3)： 210-214.

[4]刘海兰， 李小平， 芮延年. 基于时域平均和Hilbert-Huang变

换的时频嫡理论轧机齿轮箱故障诊断[J]. 机械传动， 2011， 35(9)： 54-57.

[5]扈玉辰. 基于LMD和循环平稳解调的齿轮箱故障诊断技术[D]. 太原： 中北大学， 2014.

[6]程军圣， 张亢， 杨宇. 基于噪声辅助分析的总体局部均值分解方法[J]. 机械工程学报， 2011， 47(3)： 55-62.

[7]Smith J S. The Local Mean Decomposition and Its Application to EEG Perception Data[J]. Journal of the Royal Society Interface， 2005， 2(5)： 443-454.

[8]Wu Z H， Huang N E. Ensemble Empirical Mode Decomposition: A Noise-assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis， 2009， 1(1)： 1-41.

[8]李慧梅， 安钢， 黄梦. 总体局部均值分解法在坦克变速箱滚动轴承故障诊断中的应用[J]. 装甲兵工程学院学报， 2013， 27(2)： 37-42.

[10]杨勇. EMD和模糊神经网络在滚动轴承故障诊断中的研究与应用[D]. 太原： 太原理工大学， 2008.

[11]秦太龙， 杨勇， 程琦. 基于IMF能量矩和神经网络的轴承故障诊断[J]. 振动、测试与诊断， 2008， 28(3)： 32-36.

(责任编辑: 尚菲菲)

Feature Extraction Method for Tank Gearbox Based on ELMD

LI Hui-mei1, FENG Hui-juan1, AN Gang2, WANG Shuo3

(1. Department of Military Vehicle, Academy of Military Transportation, Tianjin 300161，China；2. Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China;. Troop No. 95900 of PLA, Kaifeng 47500, China)

Abstract：Aiming at the complexity and the uncertainty of the gearbox fault vibration signal, a feature extraction method named Ensemble Local Mean Decomposition (ELMD) energy moment is presented. The vibration signals acquired from the actual tank gearbox with normal, bearing pitting corrosion and gear rupture are respectively calculated. The analysis results show that the feature can reflect gearbox conditions well and can be used to diagnose gearbox faults.

Key words:tank gearbox; feature extraction; ELMD; energy moment

文章编号：1672-1497(2016)02-0054-04

收稿日期：2016-01-22

作者简介：李慧梅(1978-)，女，讲师，博士。

中图分类号：TJ81+0.6

文献标志码：A

DOI：10.3969/j.issn.1672-1497.2016.02.011