平均横向动量随多重散射数的变化

王宏民， 王　洋， 孙献静

(1. 装甲兵工程学院基础部， 北京 100072； 2. 中国科学院高能物理研究所， 北京 100049)

平均横向动量随多重散射数的变化

王宏民1， 王洋1， 孙献静2

(1. 装甲兵工程学院基础部， 北京 100072； 2. 中国科学院高能物理研究所， 北京 100049)

摘要：基于色玻璃凝聚理论建立了唯象模型,利用该模型研究了高能质子-质子(铅核)碰撞过程中产生带电强子的平均横向动量，通过对ALICE合作组最新实验数据的χ2分析获取了唯象模型的参数值，并在此基础上计算得到了不同碰撞能量下带电强子平均横向动量随多重散射数变化的曲线。通过与实验数据比较发现：对于质子-质子碰撞过程，理论值与实验数据符合得很好；而对于质子-铅核碰撞过程，即使在多重散射数较小时，理论值与实验数据仍有一定的偏差。

关键词：平均横向动量； 带电强子多重散射； 唯象模型

高能质子-质子(核)碰撞过程中产生的带电强子平均横向动量是反映高能碰撞过程中强子物质退禁闭性质的一个重要信号，对其研究具有非常重要的物理意义。2013年，欧洲大强子对撞机(Large Hadron Collider， LHC)ALICE合作组给出了一套关于带电强子平均横向动量的实验数据[1]，为深入开展该研究提供了可靠依据。目前，国内已开展了该方面的研究[2-7]，并建立了一些理论模型，如双组分模型[2]、多重玻密子交换模型[3]等。笔者在前人研究的基础上对平均横向动量问题进行如下研究：1)利用色玻璃凝聚理论计算不同碰撞能量下的平均横向动量值，并与实验数据进行比较；2)通过推导建立带电强子平均横向动量随多重散射数变化的唯象模型，在假定模型参数值随碰撞能量增加而增大的前提下，通过对ALICE合作组最新实验数据进行χ2分析[8-9]获取模型参数值；3)利用所建的唯象模型计算得到质子-质子(proton-proton, p-p)和质子-铅核(proton-lead, p-Pb)碰撞过程中带电强子平均横向动量随多重散射数变化的曲线，并与实验数据进行比较。

1平均横向动量计算方法

根据色玻璃凝聚理论，高能碰撞中胶子多重散射截面[10-12]为

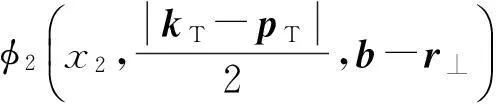
(1)

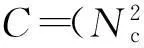
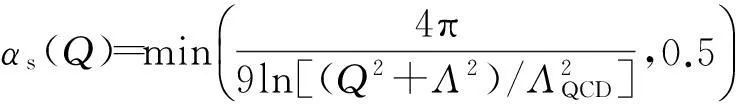
(2)

为跑动耦合常数，且Λ=ΛQCD=0.2 GeV。

在KLN(Kharzeev Levin Nardi)模型中[13]，未积分胶子分布函数φ为

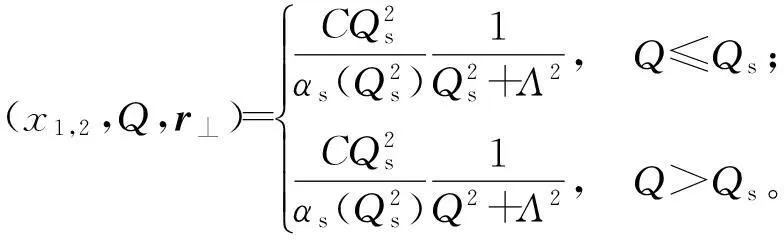
(3)

式(3)中，饱和标度为

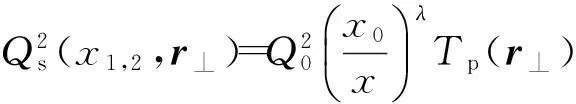
(4)

式(4)中，Q0=1 GeV，x0=0.01，λ≈0.3[14]；Tp(r⊥)为质子厚度函数，笔者采用偶极子形式[15]，即

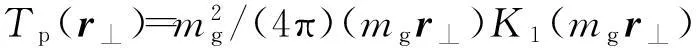
(5)

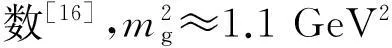
由式(1)可得平均横向动量为

pT。

(6)

2平均横向动量随多重散射数变化的唯象模型

为了得到平均横向动量随多重散射数Nch变化的关系，令

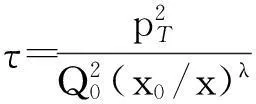
(7)

当快度y≈0时，

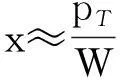
(8)

由式(7)、(8)可得

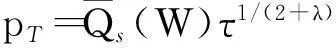
(9)

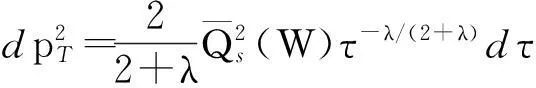
(10)

式中：

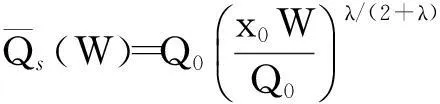
(11)

利用式(9)可将式(1)转化为关于变量τ的函数，令

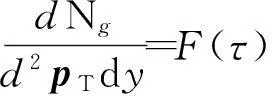
(12)

相应地，

(13)

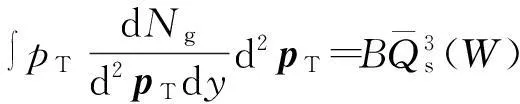
(14)

式中：

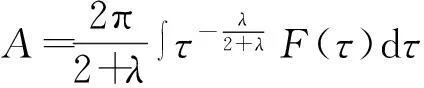
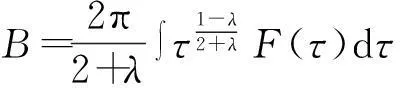
将式(13)、(14)代入式(6)，可得

pT。

(15)

带电强子多重散射数Nch与dNg/dy的关系为

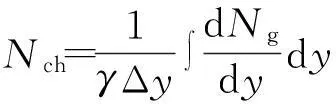
(16)

式中：γ为胶子多重散射数与强子多重散射数的关系系数。

由于ALICE合作组实验数据的测量范围为Δy=0.6[1]，在这一测量范围内可近似地认为dNg/dy为常数，则式(16)可近似为

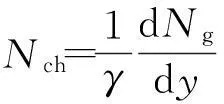
(17)

式(15)可相应地近似为

pT。

(18)

pT。

(19)

笔者假定不同碰撞能量下β与Wλ/(2+λ)成正比, 根据式(11)、(15)可得不同碰撞能量下的平均横向动量为[5]

pT，

(20)

式中：W0=7TeV，β0为相应的比例系数。

3计算结果与讨论

3.1不同LHC试验室碰撞能量下的平均横向动量

由式(6)可得到质子-质子碰撞中不同能量下的平均横向动量，并与LHC实验室ALICE合作组的最新实验数据进行比较，结果如表1所示。由表1可以看出：理论结果均在实验误差范围内，这一结果进一步验证了色玻璃凝聚理论的正确性。

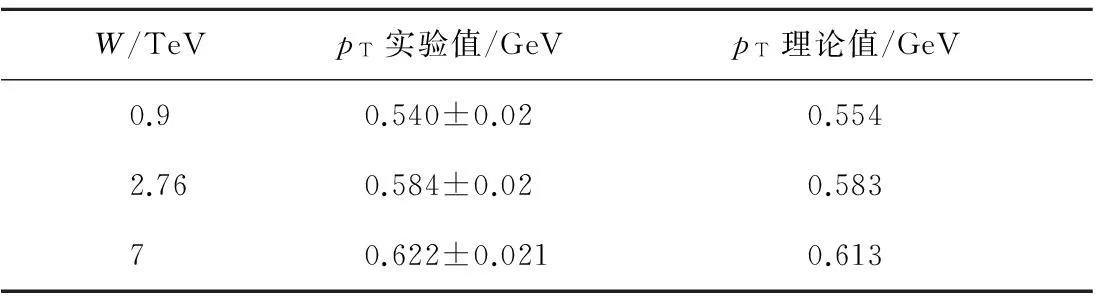
表1　不同碰撞能量下的平均横向动量

3.2p-p碰撞中平均横向动量随多重散射数变化

为了得到参数α和β0的值，笔者对ALICE合作组的实验数据进行了χ2分析[8-9],χ2分析式为

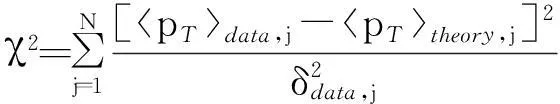
(21)

通过计算发现：当α=0.424 GeV、β0=0.072 GeV时，χ2最小，因此选其为唯象模型的参数值。图1为p-p碰撞过程中平均横向动量随多重碰撞数变化的曲线。其中：◆、▲、●分别为LHC实验室碰撞能量下W=7，2.76，0.9 TeV时，ALICE合作组实验数据[1]；★为相对论重离子对撞机(Relativistic Heavy Ion Collider, RHIC)能量下W=0.2 TeV时，PHENIX合作组实验数据[18]；实线为与不同碰撞能量下实验数据相对应的，利用唯象模型算出的理论结果，虚线为LHC能量下W=14 TeV时的理论预测值。由图1可以看出：1)当W=0.2 TeV，Nch较大时，理论值与实验值稍有偏差；2)当W=7 TeV，Nch很小时，理论值与实验值稍有偏差；3)总体来看，理论值均在实验误差允许的范围内，这一结果验证了唯象模型的正确性。

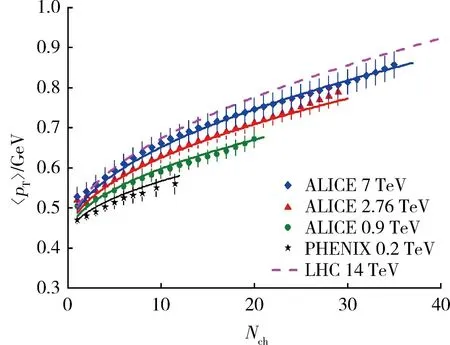
图1　p-p碰撞中平均横向动量随多重散射数变化曲线

3.3p-Pb碰撞中平均横向动量随多重散射数变化

图2为当W=5.02 TeV时,p-Pb碰撞过程中平均横向动量随多重散射数变化的曲线，实验数据来自文献[1]，其中，实线为采用与p-p碰撞过程相同的参数值计算得出的理论结果，显然，理论结果与实验数据相差较远，这是因为p-Pb碰撞过程中需要考虑核效应，与p-p碰撞过程产生带电强子的物理机制有所不同。为了得到较好的理论结果，利用式(19)重新对实验数据进行拟合，得到新的参数值为α=0.603 GeV，β=0.026 GeV，其中虚线为利用唯象模型算出的相应理论结果。

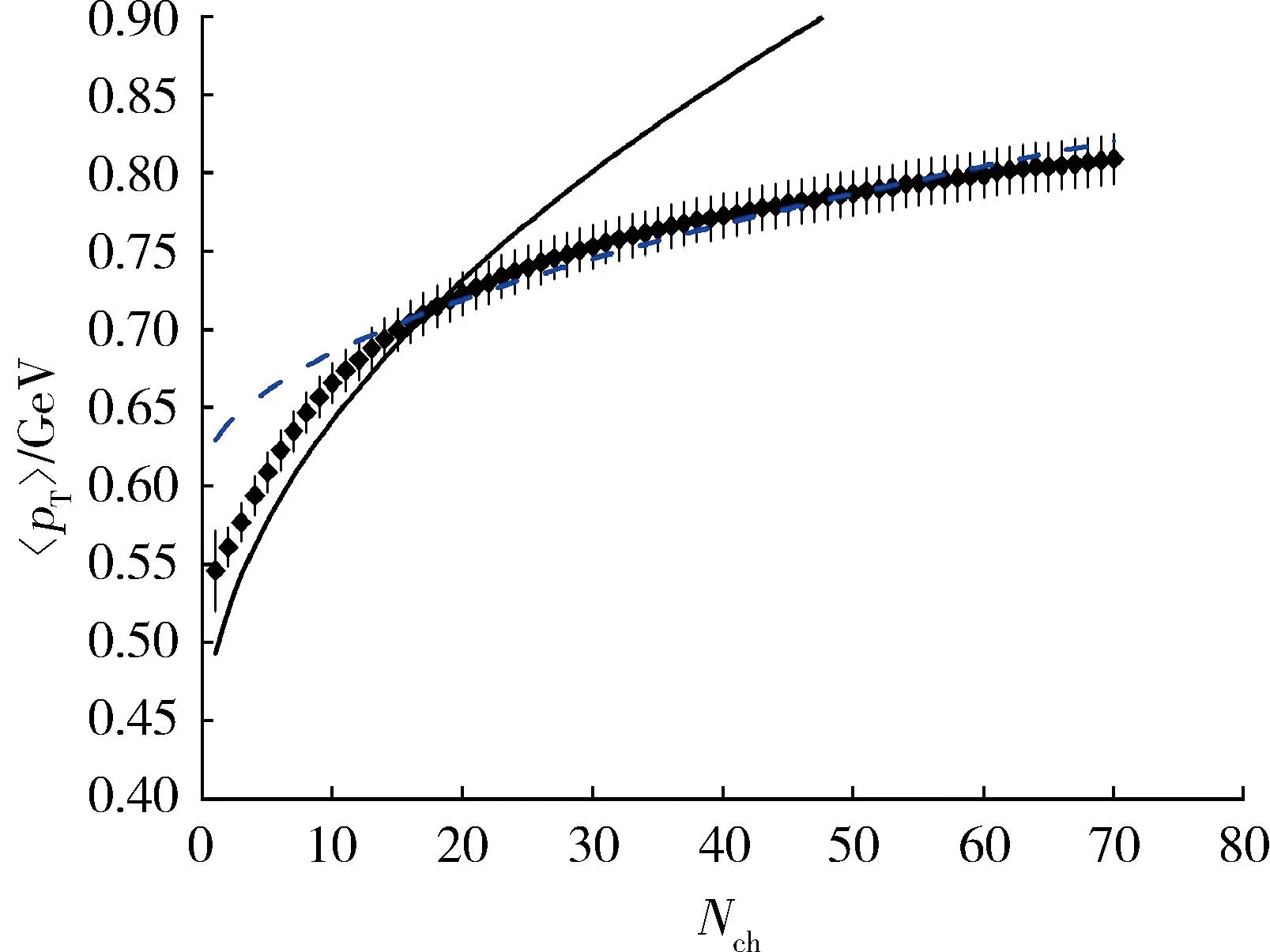
图2　p-Pb碰撞中平均横向动量随多重散射数变化曲线

由图2可以看出：当Nch较小时，新的理论结果与实验数据仍有较大的偏差。唯象模型在解释p-Pb碰撞过程产生带电强子的平均横向动量问题时出现较大偏差，说明模型对该过程的物理机制研究尚不够深入，需要进行更深入的理论研究，下一步笔者将重点研究通过引入反映新物理机制的参数来解释相关实验现象。

4结论

通过对高能p-p及p-Pb碰撞过程中产生带电强子平均横向动量问题的研究，得出如下结论：建立在色玻璃凝聚理论基础上的唯象模型是研究p-p碰撞过程中产生带电强子平均横向动量问题的一种有效方法,但对于p-Pb碰撞过程仍需要更深入的理论研究。

参考文献：

[1]Abelev B, Adam J, Adamova D, et al. Multiplicity Dependence of the Average Transverse Momentum in p-p, p-Pb, and Pb-Pb Collisions at the LHC[J]. Phys Lett B, 2013, 727(4/5): 371-380.

[2]Bylinkin A A, Ryskin M G. Secondary Hadron Distributions in Two Component Model [J]. Phys Rev D, 2014, 90(1): 017501.

[5]Praszalowicz M. Geometrical Scaling for Identified Particles[J]. Phys Lett B, 2013, 727(4/5): 461-467.

[6]Velasquez A O. MeanpTScaling with m/nqat the LHC: Absence of (hydro) Flow in Small Systems[J]. Nucl Phys A, 2015, 943(11): 9-17.

[7]Wang H M, Hou Z Y, Sun X J. Energy Dependent Growth of Nucleon and Inclusive Charged Hadron Distributions[J]. Chin Phys C, 2015, 39(11): 114105.

[8]Stump D, Pumplin J, Brock R, et al. Uncertainties of Predictions from Parton Distribution Functions I: the Lagrange Multipli-

er Method[J]. Phys Rev D, 2002, 65(1): 014012.

[9]Wang H M, Hou Z Y, Zhang B A, et al.J/ψProduction in a GLAUBER Monte Carlo Frame Work[J]. Int J Mod Phys A, 2010, 25(5): 1009-1018.

[10]Kharzeev D, Levin E, Nardi M. Color Glass Condensate at the LHC: Hadron Multiplicities in pp, pA and AA Collisions[J]. Nucl Phys A, 2005, 747(2/4): 609-629.

[11]Dumitru A, Nara Y. KNO Scaling of Fluctuations in pp and pA, and Eccentricities in Heavy-ion Collisions[J]. Phys Rev C, 2012, 85(3): 034907.

[12]王宏民, 孙献静. 强子多重数分布的Glasma流管模型[J]. 装甲兵工程学院学报， 2015， 29(2): 107-110.

[13]Kharzeev D, Levin E, Nardi M. QCD Saturation and Deuteron-nucleus Collisions[J]. Nucl Phys A, 2004, 730(3/4): 448-459.

[14]Golec-Biernat K, Wusthoff M. Saturation Effects in Deep Inelastic Scattering at LowQ2and its Implications on Diffraction[J]. Phys Rev D, 1999, 59(1): 014017.

[15]Frankfurt L, Strikman M, Weiss C. Dijet Production as a Centrality Trigger for pp Collisions at CERN LHC[J]. Phys Rev D, 2004, 69(11): 114010.

[16]叶其孝, 沈永欢. 实用数学手册[M]. 北京: 科学出版社, 2008: 680-682.

[17]D’Alesio U, Echevarria M G, Melis S, et al. Perturbative and Non-perturbative QCD Effects in Transverse Momentum Distributions[EB/OL]. (2015-10-10) [2015-11-07]. http://arxiv.org/abs/1510.02881

(责任编辑: 王生凤)

Multiplicity Dependence of the Average Transverse Momentum

WANG Hong-min1, WANG Yang1, SUN Xian-jing2

(1. Department of Fundamental Courses, Academy of Armored Force Engineering, Beijing 100072, China;2. Institute of High Energy Physics, Chinese Academy of Science, Beijing 100049, China)

Abstract：By means of the phenomenological model based on the Color Glass Condensate theory, the average transverse momentum in high energy proton-proton (or lead) collisions is studied. With a χ2-anlysis of the present experimental data from ALICE Collaboration, the parameters of the phenomenological model are extracted. Then, the results for the average transverse momentum versus charged hadron multiplicity at different collision energies are calculated. It is shown that the theory results for p-p collisions are in good agreement with the experimental data, but the results for p-Pb collisions still have a little deviation with the experimental data at small multiplicity.

Key words:average transverse momentum; charged hadron multiplicity; phenomenological model

文章编号：1672-1497(2016)02-0100-04

收稿日期：2015-11-20

基金项目：国家自然科学基金资助项目(11305195/A050509)；河北省自然科学基金资助项目(A2012210043)

作者简介：王宏民(1975-)，男，副教授，博士。

中图分类号：O572.24+3

文献标志码：A

DOI：10.3969/j.issn.1672-1497.2016.02.020