基于主方程和连续时间随机游走模型的扩散方程导出
毛志,易正萍,万亚男
(铜仁学院大数据学院,贵州 铜仁 554300)
基于主方程和连续时间随机游走模型的扩散方程导出
毛志,易正萍,万亚男
(铜仁学院大数据学院,贵州 铜仁 554300)
分别从布朗运动的主方程和连续时间随机游走模型出发导出了经典的扩散方程。进一步,在加入了外力场后,得到了Fokker-Planck方程,并对描述次扩散现象的分数阶扩散方程的导出进行了研究。
扩散方程;连续时间随机游走;Laplace-Fourier变换;Fokker-Planck方程;分数阶扩散方程
扩散方程是一类重要的偏微分方程,用来描述扩散现象中物质密度的变化,通常也用于和扩散类似的现象,例如在群体遗传学中等位基因在群体中的扩散,[1]其在物理、化学、生物、材料、医学、力学等学科中有着广泛应用。[2-4]为了运用扩散方程解决应用问题,需要对其的导出及其新的应用有一个全面的认识。下面先对扩散方程的背景及其应用做简要描述。
1 扩散方程的背景及其应用
1.1 扩散方程的背景



即

交换积分次序后可得,
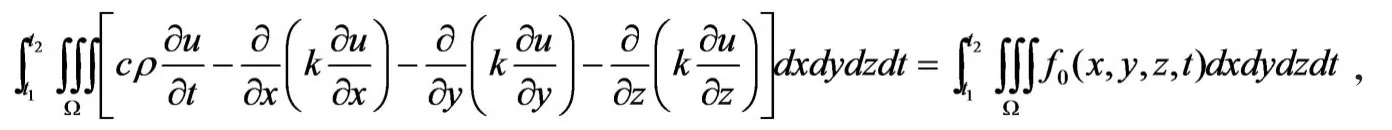

由于物体是均匀的,且各向同性,于是


第二和第三部分将分别从布朗运动的主方程和连续时间随机游走模型出发导出上述扩散方程(1)。
1.2 扩散方程的应用
扩散方程是一类基本的运动方程,它可用来描述河流、大气、土壤中污染物质的分布,流体的流动,物质中电子的运动以及生物种群的迁徙等众多现象,可用于环境科学、流体力学、能源开发和电子科学等诸多领域。无论是从数学理论还是应用科学的角度来看,对扩散方程的研究都具有极其重要的意义。近年来,扩散方程的研究已经取得了令人瞩目的进展,许多新的数学思想和方法得以发展,大大丰富了扩散方程的理论并促进了相关学科的发展。在扩散方程的基础上,发展了反应扩散方程、对流扩散方程以及吸引扩散方程等。
在物理学和工程科学中,许多模型的反应项对空间变量的依赖都具有泛函形式,它可用如下一般形式的方程来描述:[5]

2 基于布朗运动的主方程导出经典扩散方程
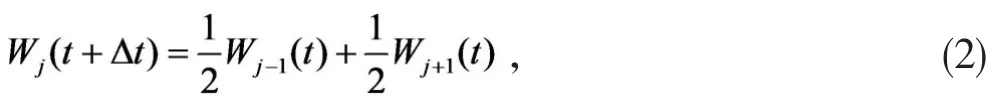

将上面两式代入(2)中得


3 基于连续时间随机游走导出经典扩散方程
本节我们首先得到基于连续时间随机游走模型的一般情形下的Laplace-Fourier变换(即关于时间变量做Laplace变换,且关于空间变量做Fourier变换)的代数关系式


(5)式对应于扩散方程(1)的Laplace-Fourier变换。具体介绍如下。
2.1 基于连续时间随机游走模型的一般情形下的Laplace-Fourier变换的代数关系式


将(9)式和(10)式代入(8)式,从而得到基于连续时间随机游走模型的一般情形下的Laplace-Fourier变换的代数关系式(4)。
2.2 基于连续时间随机游走模型的具体情形下的Laplace-Fourier变换的代数关系式


4 具有外力场的扩散方程
在具有外力场时,扩散过程通常可以利用如下的Fokker-Planck方程描述,

实际上,Fokker-Planck方程可由类似于(2)的如下主方程导出。

类似地,对(12)式进行Taylor展开后便得到Fokker-Planck方程(11)。Fokker-Planck方程描述了随机系统的状态转移概率密度,在诸如固态物理学、量子力学、理论生物学、金融等领域得到了广泛的应用。[15]
5 描述次扩散现象的分数阶扩散方程


6 结束语
本文从布朗运动的主方程和连续时间随机游走模型两个不同方面出发,利用Taylor展开、Laplace变换和Fourier变换等工具,导出了经典的扩散方程。进一步,在加入外力场后,通过主方程类似地获得了Fokker-Planck方程,并对描述次扩散现象的分数阶扩散方程的导出进行了研究。我们将在当前研究的基础上,对反常扩散理论进行研究。[18]
[1]L.H.Daniel,G.C.Andrew.Principle of Population Genetics(4th edition)[M].Sunderland:Sinauer Associates,Inc.,2007:143-144.
[2]J.Yepez.Quantum lattice-gasmodel for the diffusion equation[J].International JournalofModern PhysicsC,2001(9):1285-1303.
[3]J.M.Burgers.The nonlinear diffusion equation:asymptotic solutionsand statistical problems[M].Berlin: Springer Science&BusinessMedia,2013:105-112.
[4]Ph.Benilan,H.Brezis.Nonlinear problems related to the Thomas-Ferm iequation[J].J.Evol.Equ.,2004 (1):673-770.
[5]向昭银.关于几类扩散方程(组)解的研究[D].成都:四川大学,2006.
[6]Ph.Souplet.Blow-up in nonlocal reaction-diffusion equations[J].SIAM J.Math.Anal.,1998(29): 1301-1334.
[7]Ph.Souplet.Uniform blow-up profiles and boundary behavior for diffusion equations w ith nonlocal nonlinear source[J].J.DifferentialEquations,1999(153):374-406.
[8]J.R.Cannon and H.-M.Yin.A class of non-linear non-classical parabolic equations[J].J.Differential Equations,1989(79):266-288.
[9]J.M.Chadam and H.-M.Yin,An iteration procedure for a classof integrodifferentialequationsof parabolic type[J].J.IntegralEquationsApp,1989(2):31-47.
[10]包景东.分数布朗运动和反常扩散[J].物理学进展,2005(4):360.
[11]R.Metzler,J.Klafter.The random walk'sguide to anomalous diffusion:a fractional dynam icsapproach [J].PhysicsReports,2000(1):3-22.
[12]R.Metzler,J.Klafter.The restaurantat the end of the random walk:recentdevelopmentsin the description ofanomalous transportby fractionaldynam ics[J].JPhys,2004(31):161.
[13]刘建新.几类反应扩散方程的分支理论及应用[D].哈尔滨:哈尔滨工业大学,2012.
[14]R.Metzler,J.Klafter.Anomalous transport in external fields:continuous time random walksand fractionaldiffusion equationsextended[J].PhysicsReview E,1998(2):1621-1633.
[15]H.Risken.The Fokker-Planck equation:Methods of solution and applications[M].Berlin:Springer, 1989:325-348.
[16]常福宣,陈进,黄薇.反常扩散与分数阶对流-扩散方程[J].物理学报,2005(3):1113.
[17]R.M etzler,J.Klafter.The random walk'sguide to anomalous diffusion:a fractional dynam ics approach [J].PhysicsReports,2000(339):3-22.
[18]陈文,孙洪广,李西成.力学与工程问题的分数阶导数建模[M].北京:科学出版社,2010:202-216.
Deriving the Diffusion Equation from theM aster Equation and Continuous Time Random W alk M odel
MAOZhi,YIZheng-ping,WANYa-nan
(Big Data Institute,Tongren University,Tongren,Guizhou554300,China)
In this paper,we derive the classical diffusion equation from themaster equation of Brownianmovement and continuous time random walk model.In the presence of an external field,Fokker-Planck equation isobtained.Wealso derive the fractionaldiffusion equation describing subdiffusion.
Diffusion Equation;Continuous Time Random Walk;Laplace-Fourier Transform;Fokker-Planck Equation;FractionalDiffusion Equation
B84
A
2096-0239(2016)06-0106-07
(责编:任秀秀 责校:明茂修)
2016-10-20
贵州省科技合作计划项目“分数阶最优控制问题的高精度高效算法研究”,项目编号:黔科合LH字[2015]7247号;2016年国家级大学生创新训练计划项目“基于大数据的武陵山区旅游精品路线研究”,项目编号:2016106678;贵州省普通高等学校创新人才团队项目“贵州省普通高等学校分数阶微分方程数值解法及其应用创新团队”,项目编号:黔教合人才团队字[2015]64。
毛志(1982-),男,湖南汨罗人,铜仁学院大数据学院副教授,数学博士。研究方向:微分方程及其应用。

