“标准米”之谜的澄清与解决——从“逻辑行动主义方法论”的视角看

冯立荣，王丽

（吉林师范大学政法学院，吉林 四平 136000）

“标准米”之谜的澄清与解决
——从“逻辑行动主义方法论”的视角看

冯立荣，王丽

（吉林师范大学政法学院，吉林 四平 136000）

“逻辑行动主义方法论”的要旨在于严格界划由言语行动之产品构成的“语言域”、由心智行动之产品构成的“思想域”以及由客观行动的对象构成的“对象域”。“标准米”是当今学界最受争议的先验-偶然知识谜题。使用逻辑行动主义方法论可以澄清相关研究中存在的诸多混乱，揭示出标准米示例不具备先验-偶然知识资质的真正原因，同时也可以为进一步说明先验-偶然知识论题的合理性奠定基础。

逻辑行动主义;标准米;先验;偶然;知识

“逻辑行动主义方法论”是国内学界在探讨当代逻辑哲学前沿难题过程中所获得的一个新颖工具，有时也可称为“分析的行动主义”。这一方法论的要旨在于：“以严格界划由言语行动之产品构成的‘语言域’、由心智行动之产品构成的‘思想域’以及由客观行动的对象构成的‘对象域’为特征，通过诉诸以客观行动为根基的三类行动及其相互作用机理而解决哲学难题”。[1]具体可构图如图1：

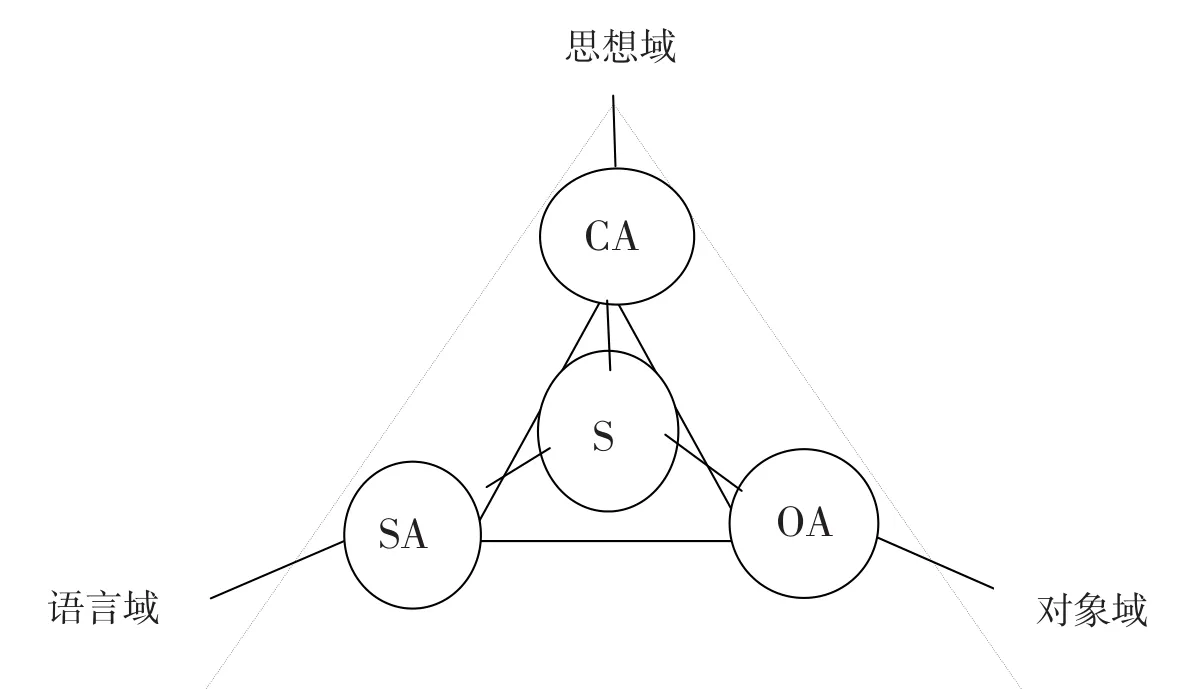
图1 思想域、语言域、对象域三类行动构成图

其中，SA表示言语行动，CA表示意识或心智行动，OA表示客观行动，S表示行动或认知主体。

“标准米”之谜是先验-偶然知识示例中比较著名的一个例子。从相关研究的实际历程来看，学界关于它的讨论可以分为两类：一类属于穆勒主义，另一类属于非穆勒主义。通过考察可以发现：即使在指称理论上坚持穆勒主义的学者，对“标准米示例是否构成真正的先验-偶然知识”这类问题也是莫衷一是。本文试图借助逻辑行动主义方法论批判性考察国内外关于标准米示例的研究所存在的诸多混淆，揭示出它之所以不具备先验-偶然知识资质的真正原因，为进一步说明先验-偶然知识的合理奠定基础。

一、作为先验-偶然知识的标准米示例

维特根斯坦（L.Wittgenstein）曾把一米标准归为“不可说”之物：“有一个事物，人们既不能说它是一米长，又不能说它不是一米长，它就是保存在巴黎的作为标准米的那根金属杆。”[2]但克里普克表示强烈质疑：“维特根斯坦一定是错了。若有一根棍子，它有一定的长度，比如39.37英寸，那么，为什么不能说它是一米长？”[3]在克里普克看来，标准米实际上是一个典型的先验-偶然知识。使用S表示那根棍子，标准米示例可以刻画为（1）：

（1）S在t0时刻的长度是一米。

围绕（1），克里普克给出了三个相互联系的论据。

第一，区分严格指示词与非严格指示词。“S在t0时刻的长度”在直觉上是限定摹状词，应该属于非严格指示词。“一米”在直觉上是名称，属于严格指示词。鉴于（1）由两种不同类型的表达式构成，从逻辑行动主义所界定的“对象域”的角度来说，就是名称所指的对象有可能不具有摹状词所描述的性质，从而与（1）相关的本体论模态就是“偶然”。

第二，严格区分指称固定（reference-fixing）与意义给予（meaning-giving）。在克里普克看来，（1）只是一种指称固定。其中，“一米”指的是那个事实上唯一满足“S在t0时刻的长度”所描述性质的对象。由于“S在t0时刻的长度”只是固定“一米”的指称而非给予其意义，又依据直接指称理论，“一米”可以直接指达世界中的那个对象，所以，与（1）相关的认识论模态就是“先验”[3]56。

第三，严格区分形而上学范畴与认识论范畴。必然/偶然是形而上学范畴：如果世界事实上如此，且有可能不如此，那么就是偶然；如果世界事实上如此，且不可能不如此，那么就是必然。先验/后验是认识论范畴：如果我们依赖经验认识到某种情况，那么就是后验；如果我们没有依赖经验认识到某种情况，那么就是先验。一旦严格区分形而上学范畴与认识论范畴，（1）的先验-偶然性就变得十分自然。

就上述论据而言，学界不乏赞同者。但关于“（1）是否具有先验-偶然知识的资质”这一问题，即使是直接指称阵营的学者也都表达出了各种各样的质疑。从逻辑行动主义方法论的视角看，这些质疑侧重于从“思想域”或“对象域”考虑，例如：内森·萨蒙（N.Salmon）认为与标准米相关的应该是“后验”；范布拉克尔与艾瑞克·卢米斯（E.Loomis）认为与标准米相关的应该是“必然”。除此之外，学界关于标准米示例的研究还体现在从行动、表达式的使用规范或规则等角度，例如：卢米斯认为标准米示例在维特根斯坦那里涉及的是断言行动；萨蒙认为从标准米示例可以导出一个知道行动的“怀疑论”情境。

二、作为后验-偶然知识的标准米示例

假设用“勒斯”命名S在t0时刻的长度。用“普洛普泽生”命名“S在t0时刻的长度是勒斯”这个语句所表达的命题。萨蒙表示，“普洛普泽生”所指的命题是“罗素型命题”，所以其主要构成部分就是：与勒斯相关的概念以及S在t0时刻的长度。基于此，萨蒙强烈怀疑一个认知主体可以不依赖经验获得一个关于具体长度的知识：“他（她）要么是看（look at）一眼S在t0时刻的长度，要么是被告知S在t0时刻正好是那个长度（that length）。无论如何，关于（1）的知识应该是‘后验’的”[4]。

萨蒙逐次提出了四个论据：第一，理论上，即使可以在没见过S的前提下通过“S在t0时刻的长度”引入“一米”，但只有当指称固定者看过，或被他人告知S在t0时刻的长度之后，“普洛普泽生”所指的命题才可以成为知识。更关键的是，克里普克曾亲自告知萨蒙，（1）所相关的指称固定过程是：指称固定者先是看到S，然后指称性地去指那个长度。在这种情况下，萨蒙更坚定地认为（1）是后验的。

第二，或可把（1）改造为（2）：

（2）S在t0时刻的长度是指称固定者所意指的那个“一米”。

从（2）可以看出：只要指称固定者知道“一米”指称勒斯这个长度，那么就可以知道S在t0时刻的长度是一米。但在萨蒙看来，实际顺序恰好相反：首先是发现S在t0时刻具有勒斯这个长度，然后推知“一米”指称勒斯，所以，关于标准米示例的知识就是“后验”的。

第三，即便“理解命题”的经验与“相信命题”的经验具有区别，但由此不能推出与标准米示例相关的认识论模态就是“先验”。萨蒙认为，看见S的视觉经验既在理解相关命题又在相信相关命题方面发挥了关键作用。所以，与标准米相关的知识是后验。

第四，在S是唯一长度标准的条件下，尽管不能实际去测量S的长度，但若想获得标准米的知识必须要有某些经验。一定意义上来说，看到S，也就意味着看到了S的长度，而在萨蒙看来，这个视觉经验恰好可以证明关于标准米示例的知识是“后验”的。

表面上看，萨蒙的上述反驳还是比较全面的。但正如前文已经指出，其最主要的论据是以他所阐述的与标准米相关的罗素型命题理论为前提的。实际上，依逻辑行动主义方法论的基本观点，如果我们对萨蒙进行追问，所谓的“先验-偶然知识”，其载体到底是什么，那么，上述四个论据的说服力都会大打折扣。如果能够严格区分逻辑行动主义所澄清的“思想域”与“对象域”，那么即使可以假设先验/后验知道的载体是“命题”，偶然的载体，至少是直接载体决不能还是“命题”。国内外相关研究普遍存在一个误解：先验-偶然知识的所有载体都是“命题”。这种观点实际上既预设了“思想域”与“对象域”的同一，又预设了“命题”与命题所表征“事态”的同一。若想清楚揭示标准米示例的真实面貌，必须严格区分“命题”与命题所表征的“事态”，即要指出：在同一情境之中，先验知识的载体与偶然的载体决不能是同一个，前者暂且可以看作是“命题”，而后者只能是命题所表征的“事态”。

精确来看，事态由对象及其属性构成，但由此不能推出表征事态的命题也由对象及其属性构成。尽管事态与实在世界相关，但由此不能得出，关于表征这个事态的命题的知识一定是“后验”的。如果能够严格区分“命题”与其所表征的“事态”，那么首先，构成标准米示例所表达命题的部分之一决不能是世界中的长度，而只能是关于这个长度的概念或表征，其次，与标准米相关的认识论模态也可以是“先验”。萨蒙一再坚持，看到S及其长度的视觉经验既充当了理解命题又充当了证立相信命题的作用，但他并没有为后一个作用提供任何论证。如果我们把视觉经验解读为理解相关命题的经验，那么，相信（1）所表达的命题似乎就可以不依赖经验，如此就有充足空间去论证与（1）相关的认识论模态是“先验”了。

笔者认为，萨蒙的核心反驳犯了“虚假二分”谬误：尽管萨蒙已经认识到需要严格区分相信一个命题的经验与理解一个命题的经验，但在实际论证过程中并没有完全排除把关于S的视觉经验处理为理解相关命题的经验，从而依然可以论证与（1）相关的认识论模态是“先验”这样一种可能性。笔者正是从这样一种可能性出发认为，与（1）相关的认识论模态是“先验”。同时，也需强调指出：笔者所使用的“先验”概念与克里普克的具有重大差异。在后者看来，“‘标准米’是一种先验知识”是直接指称理论的主要后果之一。这一论证思路容易把“先验”解读为“无需任何经验”，而直接指称理论恰与这种用法相通。但是，我们也可把“先验”解读为“无需任何经验，理解命题的经验除外”。不难发现，这种解读可以容许我们在不预设直接指称理论的前提下，说明“标准米”示例作为先验知识的合理性。

三、作为先验-必然知识的标准米示例

“与‘标准米’示例相关的是必然性”这一观点分别获得了范布拉克尔与卢米斯两位学者的支持。借助克里普克自然种类词的理论，范布拉克尔具体提出了四个论据，以论证“标准米”示例的必然性。

第一，严格区分“等于一米（=1米）”与“约等于一米（≈1米）”。[5]由于我们使用“S在t0时刻的长度”去固定“一米”的指称对象，所以，（1）在范布拉克尔看来应该解释为（3）：

（3）S在t0时刻的长度=1米

要想判断任意对象，例如，一抹红布或一条哈达的长度，最好的方法就是拿它们与S比较。假设红布与哈达的两端正好与S的两端吻合，那就可以说它们长一米。但依上述区分，它们的长度只能是约等于一米。

第二，严格区分“长度单位”的性质与“长度单位标准”的性质。对于同一个长度单位，历史上出现了很多标准，但长度单位本身是个常量。而且，仔细考察历史上出现的不同标准，其间所涉及到的性质大多可以归为自然种类的性质。

第三，区分作为名称的严格指示词与作为限定摹状词的严格指示词。范布拉克尔认为，“S在t0时刻的长度”与“一米”都是严格指示词，所以，（3）在本质上与“晨星=暮星、西塞罗=图利”是相通的。

第四，适当区分“先验构造的理论同一性”陈述与“后验发现的理论同一性”陈述。假设克里普克关于自然种类的本质学说成立，即，如果赞同H2O是水分子的本质属性，原子数为79是黄金的本质属性，那么就应该赞同（3）表示的是一种“理论同一性”。如果是理论同一性，那么与标准米相关的本体论模态应该就是“必然”。

与范布拉克尔不同，卢米斯则是从澄清“标准”意义的角度来论证标准米示例的必然性的。他认为，“标准”的一般性定义可用DS概括：

第一，无论是选择“S”还是“S的长度”作为一米的标准，我们都无法进行反事实设想。假设S是一米的标准，那么根本就不存在另一个独立的长度标准容许我们有意义地说S有可能不是一米长。假设一米的标准是一个特定长度，L。如果有个体拥有这个长度，那么这个个体也可以间接成为一米的标准。即使是这样，我们也不能对标准米示例进行反事实设想。首先，没有任何理由去说L可能不是一米长，因为L是一米的标准。其次，尽管表面上可以设想S有可能不是一米长，但这只是因为，在逻辑上S有可能不是标准。

第二，假设一米的标准是长度L，克里普克的“温和实在论”表明，无法对（1）进行反事实设想。依据温和实在论，如果L是一米的标准，那么设想的结果就是：现实世界中的那个S在t0时刻所具有的那个实际长度有可能不是一米。依据现实性的逻辑理论（logic of“actually’），现实世界中的那个S在t0时刻所具有的那个实际长度是一米应该是“必然的”。依据DS，卢米斯认为（1）的“必然性”是确定无疑的，因为对（1）进行反事实设想实际上意味着否定个体的自我同一。

对比考察范布拉克尔与卢米斯关于必然性的论证，笔者认为前者要优于后者。首先，一定意义上来说，范布拉克尔与克里普克两位学者之间的重要差异可以归结到对“是”的理解上。克里普克是在“谓述”的含义上，而范布拉克尔是在“等于”的含义上使用“是”的。依据对“是”的不同理解，我们关于反事实设想的结果也会不同：选择一个事物作为长度的标准具有一定的任意性，但由此不能得出，该长度是事物的偶然性质。例如，克里普克在探讨标准米示例时还曾使用过另一种刻画（4）：

（4）S在t0时刻有1米长。

他由可以对（4）进行反事实设想推出与（4）相关的是“偶然”模态。但显然，如果对“是”进行“等于”理解，对（4）进行反事实设想，实际上就是在设想选择另一个事物作为标准，这已经与S没有任何关系了。

其次，笔者对卢米斯的DS也有疑义。卢米斯特别强调，DS中的“逻辑推出”非常重要，决不能把标准一般地定义如下：

可以看出，DS*要比DS弱。但是，DS*为什么就不能成为标准的一般性定义？在逻辑上，有时候需要采取弱化立场，这或许就是“从弱原则”的价值所在。卢米斯只是指出DS*太弱了。但在笔者看来，DS至少在表述上是不严格的。其中的“逻辑推出”到底是什么意思？另外，DS应该是个高阶公式，但性质P却没有被量化，s也没有。所以，笔者试图提出一个替代公式MDS：

MDS:（s）（P）s是性质P的标准，当且仅当（x）(x与s等长□Px)

其中，MDS表示修改后（modified）的标准定义，s和P在其中被全称量词所约束，“□”表示必然，其他解释如DS。可以看出，由于MDS是一个模态公式，所以其与DS在本质上不同。尤其是，MDS所包含的“□”符号还可以与范布拉克尔关于“必然性质”的论据相对应。当然，笔者关于标准米示例上的必然性立场独立于MDS。MDS的价值在于，如果它是合适的定义，那么依据它可以为范布拉克尔、卢米斯以及笔者的核心观点提供一个新的论证思路。

综合以上内容，笔者给出本文的第一个观点：由于与标准米示例相关的两种模态应该是先验-必然，所以，它不是一个成功的先验-偶然知识。当然，由此不能推出先验-偶然知识论题不具有合理性。国内有学者曾就依据标准米示例不成功推出“克里普克没能否定‘先天（验）的’也是必然的”。[7]笔者认为，这一观点值得商榷。首先，这个观点中“没能否定”的结论本身具有一定的模糊性。是全称还是特称？如果是全称，那么对它的否定应该是“有些先验的不是必然的”。从“有些”并不能推出具体是哪些，所以，决不能从一个案例不成功直接推出克里普克的观点不正确。其次，如果是特称，那么它与克里普克使用标准米示例所要证明的结论是相容的。标准米示例不成功，只能说论据有问题，但不能得出克里普克试图证明的论点不正确，因为，还存在其他示例。

四、作为不可说的标准米示例

考察完学界关于克里普克立场的研究之后，本节重点关注学界对维特根斯坦的辩护。首先考察卢米斯对维特根斯坦的辩护。从其论题（Necessity,The a prioriand The Standard Meter）可以发现，他旨在说明维特根斯坦是在“必然性”意义上讨论标准米示例的，他把这种“必然性”称为维特根斯坦式的“广义的约定主义者的必然”，其与语言的使用规则相关。他的这一部分论证主要是通过对比维特根斯坦与克里普克在标准米示例上的根本差异来完成的。

第一，对于标准米示例，维特根斯坦关注的是其规范功能。维特根斯坦的一米标准是S，而不是S的长度。他之所以对S“不说”，主要是因为不能使用（1）去断言一个或真或假的语句。若想断言一个个体是一米长，那么必须通过某种测量方式使得这个个体与一米标准的两端对齐。对于一米的标准本身，我们无法实际地使它与自己的两端对齐，因此，既无法断言一米标准是一米长，又无法断言一米标准不是一米长。

第二，对于标准米示例，克里普克强调的是其描述功能。克里普克的一米标准是S的长度。如果知道一个个体长39.37英寸或者三又三分之一尺，那么就可以换算出这个个体长一米。由于S在t0时刻所具有的长度正好是那个标准长度，所以，当然可以说S在t0时刻长一米。澄清两位学者之间的差异之后，卢米斯指出，由于在维特根斯坦那里标准米示例本质上一个行动规范或规则，它规范着如何使用“一米”这个表达式，因此可以看作是一种约定主义的必然真理。

除卢米斯之外，萨蒙也曾对维特根斯坦的“不可说”观点进行过辩护。他把我们关于标准米的情景概括为“是否知道F，其中，F表示‘多长’、‘是谁’或者‘多少’等性质”。“在有些语境里，知道一个长度标准的名字就可以算作知道是哪个长度；但在其他语境里，并非如此。”[4]214在标准米示例中，对于任意对象，若想知道其长度，其充要条件是实际的测量。但对于一米的标准来说，指称固定者自动地满足了这个条件。看到S的长度就可以算作是对S进行了测量。观察可以说是一种测量的极限情况。另一方面，当询问指称固定者是否知道S本身是多长时，已经从语言游戏的内部转换到了外部。从外部来看，知道S本身是多长需要拿S与高阶的标准相比较。但指称固定者并不能接触到这个高阶标准。萨蒙认为，这个“知道F”的情境似乎可以为维特根斯坦的“不可说”观点进行辩护：“如果说出了某件自明的事物可以导致我们必须进一步说出若干更令人震惊的事物的话，我们最好还是对这个事物保持沉默”。[4]217

整体上来看，萨蒙与卢米斯的核心观点都有一定的合理性。但笔者也试图针对“知道F”的怀疑论情境提出一个质疑。依“语言域”、“思想域”以及“对象域”的区分，上述“F”应该属于哪一域？很明显，萨蒙认为其应该在“对象域”。但正如前文已经澄清，无论是知道还是相信，其对象是命题，而命题及其构成部分应该属于“思想域”。这是萨蒙观点的一个重大混淆。笔者认为，澄清这一点对于批判性考察维特根斯坦“不可说”观点的价值具有重要作用。

五、先验-偶然知识论题的合理性

与批判性考察学界关于“标准米”示例研究密切相关的一个更一般的问题是：先验-偶然知识论题是否具有合理性？在笔者看来，答案是“肯定”的。本节旨在正面给出一个新颖说明。按照逻辑行动主义方法论的解释，所谓先验-偶然知识论题的含义是非常丰富的：“语句”、“语词”属于“语言域”，“命题”、“概念”属于“思想域”，而“对象”、“性质”属于“对象域”。语句（语词）表达命题（概念），命题表征事态。所谓一个命题为真是指该命题所表征的事态在世界之中。真命题表征的是事实。从行动哲学的视角看，上述三个域是作为相应行动的产品或对象而存在的，所以要区分言语行动、思想行动以及客观行动。其中，断言（assert）行动或可归于言语行动的一种，相信或可归到心智行动。心智行动的一个显著特征是有意向性。而且，言语行动与心智行动往往是相互伴随的。也就是说，本文所涉及到的“固定指称约定”既涉及到了言语行动又涉及到了心智行动。

所谓先验/后验是修饰“相信”这个行动的，而相信的对象是命题。以某种方式相信了一个命题可以构成一个信态（state ofbeliefs）。如此，先验/后验就是信态的属性。必然/偶然是事态的属性。本文赞同把“知识”解释为“依据某些证据相信某个命题为真”。如果其中的证据不涉及经验，那么就是“先验”；如果其中的证据涉及到了经验，那么就是“后验”。由于先验-偶然知识的载体实际上不是一个，而不同层面之间在理论上显然既有联系又有区别，所以，按照逻辑行动主义的观点，先验-偶然知识应该是比较常见的，所以其合理性也也应该是非常自然的。未来的任务在于进一步研究和说明命题、相信及其方式、事态及其属性等不同层面之间的联系机制，比如说，置信语义学、动态认知逻辑也会在这个论题上大有作为。这应该构成该论题未来研究的趋势之一。

注释：

①实际上，萨蒙并没有论证“‘一米’可以指称S在t0时刻的长度”是一个“先验”真理。笔者猜测他很可能受到了唐纳兰的启发，即认为，当前所讨论的这个“指称语句”属于一种元语言事实。这一点或可受到质疑，但萨蒙本人确实承认他的主要立场与唐纳兰的观点有类似之处，尽管后者并没有详细研讨过标准米示例。

[1]张建军，等．当代逻辑哲学前沿问题研究[M]．北京：人民出版社，2014：615．

[2]L．W ittgenstein．Philosophical Investigations[M]．New York:TheM acm illan Company,1968:section 50．

[3]S．Kripke．Nam ing and Necessity[M]．Cambridge:Harvard University Press,1972:54．

[4]N．Salmon．How to Measure the Standard Meter[J]．Proceedingsof the Aristotelian Society,1988(88)．

[5]J．Van Brakel．UnitsofMeasurementand NaturalKinds:Some Kripkean Considerations[J]．Erkenntnis,1990(33):299．

[6]E．Loom is．1999,NECESSITY,THEA PRIORI,AND THESTANDARD METER[J]．Synthese,1990(121):298．

[7]王希勇．“标准米尺是一米长”是先天的偶然真理吗？[J]．哲学研究,1996(12):49．

A Tentative Solution to the Puzzle of Standard M eter——From the Standpointof theMethodology of Logical Actionism

FENG Li-rong，WANG Li
(Schoolofpoliticsand law,Instituteof the sinicization ofMarxism,Ji Ling NormalUniversity,Siping136000)

Themethodology of logical actionism is to separate between linguistic realm,thought realm and objective realm,aswell as linguistic action,conscious action and objective action.More importantly,this methodology aims to distinguish action from their products or objects.The standardmeter is themost controversial instance of The Contingent-A Priori-Knowledge.This paper is an attempt to consider critically on almostall the debatesabout the standardmeter,reveal the genuine reason for the failure of thisexample,clarify several confusions in the relevantdiscussions and offer a kind ofnew account for the rationality of the thesis of The Contingent-A Priori-Knowledge.

LogicalActionism;The Standard Meter;The A Prior;Contingency;Knowledge

B81

A

2096-0239（2015）06-0047-06

(责编：彭麟淋责校：明茂修)

2016-10-06

教育部人文社会科学项目“偶然模态逻辑及其应用价值研究”，项目编号：15YJC72040001；吉林省社会科学基金项目“语用逻辑视域下的摹状词最新成就研究”，项目编号：2016BS7。

冯立荣（1984-），男，宁夏青铜峡人，吉林师范大学政法学院讲师，哲学博士。研究方向：现代逻辑与逻辑哲学，西方逻辑史。

王丽（1983-），女，吉林白山人，吉林师范大学政法学院硕士研究生。研究方向：道德哲学与逻辑。