莫尔应变圆极点法及应变极点特性研究

翟汉波，李大勇,刘庆松，王凯挺

(山东科技大学 a.山东省土木工程防灾减灾重点实验室; b.土木工程与建筑学院，山东 青岛　266590)

莫尔应变圆极点法及应变极点特性研究

翟汉波a,b，李大勇a,b,刘庆松b，王凯挺b

(山东科技大学a.山东省土木工程防灾减灾重点实验室;b.土木工程与建筑学院，山东 青岛266590)

摘要：极点是根据单元体的应变状态在莫尔应变圆上做出的一个特殊点，通过极点可以获得任意平面的应变状态。为确定莫尔应变圆上的极点，提出了2种方法——平行线法和法线法。采用反证法分别验证了平行线法和法线法确定的应变极点的唯一性，采用几何作图法分别验证了平行线法和法线法确定的应变极点的可靠性。研究表明：2种方法确定的应变极点位于莫尔应变圆的同一条直径上；应力极点与应变极点位于莫尔应力圆与应变圆组成的同心圆的半径上。莫尔应变圆极点法具有简便、准确的优点，避免了复杂的公式计算，是求解岩土工程中的稳定和变形问题及确定单元体复杂应变状态的优选方法。

关键词：莫尔圆；极点法；应力圆；应变圆；唯一性；旋转法

1研究背景

莫尔圆(MohrCircle)的概念来源于德国桥梁工程师KarlCulmann在1866年提出的应力可以用图解法分析的思想，Culmann证明了作用于任意斜截面上的正应力和剪应力为应力圆上的一点的坐标[1]。1882年德国土木工程师ChrisitanOttoMohr对这一课题进行了完整的研究，把莫尔圆推广应用到二维及三维应力情况，并提出了基于应力圆的强度准则[2]。从此，人们却淡忘了莫尔圆真正发明人Culmann，并一直称“MohrCircle”至今。Culmann在莫尔圆上建立了一个点，通过这个点作平行于任意平面的平行线与圆的交点即为该面上作用的应力。这个“点”被称为“极点”(Polepoint)，然而Culmann当年并没有给予它命名。极点法是莫尔圆中的一个非常重要的方法，借助极点可以用作图法方便、快速地得到复杂条件下的应力状态(应力大小和方向)而不必使用繁复的数值计算。

土力学教材中如，Terzaghi[3]，Lambe[4]，Budhu[5]，Das[6]，Holtz[7]都介绍了平行线法作应力圆极点的方法，但未涉及应变问题。材料力学中，如Gere[8]，Hearn[9]，Hibbeler[10]等都介绍了在莫尔应变圆上，由已知应变值点绕圆心旋转2α角所对应的点的方法，α为已知应变平面与未知应变平面的夹角，并未涉及极点的概念。李大勇等[11-12]证明了极点存在的唯一性，同时提出了确定莫尔应力圆极点的新方法。与公式法相比，莫尔圆极点法避免了复杂的解析计算，同时解决了利用莫尔圆旋转法不能解决的复杂应力问题。莫尔应变圆极点法可以准确求解出任意平面的应变状态，确定主应变面的位置和主应变面上应变值的大小。

本文是对文献[11-12]研究成果的推进，给出了定义应变极点的2种方法：平行线法和法线法。得到了2种不同应变极点定义下，极点在莫尔应变圆上的关系，证明了2种极点法解决平面应变问题的准确性。极点的定义方法不同，在莫尔圆上得到极点的位置也不同。当定义极点的方法确定时，莫尔圆上有且仅有一个极点，证明了2种极点定义方法下极点的唯一性。虽然这2种方法下的极点不是同一个点，但所求得的结果是相同的。说明了极点法解决复杂应变问题的优越性。最后，根据应力应变之间的关系，在莫尔应力圆与应变圆组成的同心圆上，利用平行线法作出应力极点和应变极点，得到了应变极点与应力极点之间的关系。

2莫尔应变圆极点法

2.1平行线法

单元体平面应变单元见图1(a)。根据土力学规定：压应变为正，取剪应变绕单元逆时针转动为正，反之为负。本文分析了平面单元体内部截面上的应力应变状态，采用直线表示垂直于平面单元体内部的截面。平行线法确定莫尔应变圆极点的步骤为：在ε-γ/2坐标系下(图1(b))，作点C(εx，γxy/2)，点D(εy，γyx/2)，连接C，D两点，以CD为直径作莫尔应变圆。过C点作平面ad的平行线交圆于一点P′，也可过D点作平面ab的平行线交于P′，P′即为应变极点。通过极点P′作ae面对应的平行线交莫尔应变圆于E′，交点的坐标值(εθ，γθ/2)即为该平面的应变值。

图1　应变单元体与所对应的莫尔应变圆Fig.1　Plane strain element and correspondingMohr circle of strain

2.2法线法

法线法确定莫尔应变圆极点的步骤如下:在图1(b)中，过莫尔应变圆C或D点作平面ad的法线n1的平行线交圆于一点P，该点即为法线法定义下的应变极点。通过P点作任一平面的法线的平行线与圆的交点即为对应平面的应变值点，如通过极点P作ac面法线n2的平行线交莫尔圆与E，该点的坐标值(εθ，γθ/2)即为该平面的应变值，即E与E′是同一个点。

在莫尔应变圆上(图1(b))，连接PP′，由几何关系得PC⊥P′C，点P与P′在同一条直径上。因此对于给定单元体平面应变状态，平行线法与法线法所定义的极点位于莫尔应变圆的同一直径上。

3莫尔应变圆极点的唯一性证明

给定应变状态下，莫尔应变圆上有且仅有一个极点存在，这就是极点唯一性原理，可采用反证法证明，假设在莫尔圆上的极点不唯一。此证明方法同样适用于应力极点的唯一性证明。

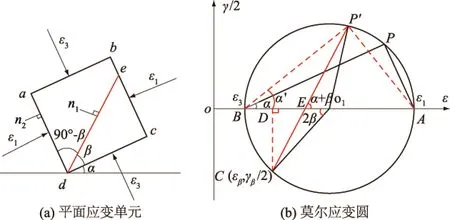
图2　平行线极点的唯一性证明Fig.2　Uniqueness proof of ploe pointby parallel line method

3.1平行线法极点唯一性证明

图2(a)为某一应变单元体，已知最大、最小主应变分别为ε1，ε3。图2(b)为应变单元所对应的莫尔应变圆，由最大、最小主应变得到应变极点P。

已知截面β上的应变(εβ，γβ/2)，过莫尔应变圆上点C(εβ，γβ/2)作该平面的平行线交应变圆于一点P′。显然，若证得P与P′不重合则原假设成立，极点不唯一。否则，原假设不成立，证明极点具有唯一性。证明过程如下：

任意β平面上的应变值可用最大、最小主应变值表示为:

(1)

(2)

作辅助线连接P′A,P′B,CO1和PO1，作CD⊥AB于D。

又有莫尔应变圆方程[9]

(3)

则直线CD的长度为

(4)

直线O1D的长度为

(5)

进而，

(6)

所以∠CO1D=2β。

在图2中，由CP′∥de，得∠P′EO1=∠DEC =α+β。

在ΔCDE中，

∠DCE =90° - ∠DEC=90° - α - β。

在ΔCO1D中，

∠O1CD=90°-∠CO1D，即∠O1CD =90°-2β。

因此，

∠ECO1=∠O1CD -∠DCE=α - β 。

进而，在ΔP′O1C中，

∠P′O1C=180°-2∠ECO1，即∠P′O1C =180°-2(α - β)，∠P′O1B=∠P′O1C-∠CO1D =180°-2α。

在ΔP′O1B中，

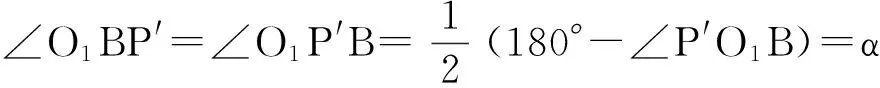
所以∠P′BA=∠PBA=α。即证明BP与BP′重合，即点P与P′重合，即证明了莫尔应变圆上利用平行线法所作的极点具有唯一性。

3.2法线法极点的唯一性证明

图3(a)为某一应变单元体，已知最大、最小主应变分别为ε1，ε3。图3(b)为应变单元所对应的莫尔应变圆，利用平面法线法由最大、最小主应变得到应变极点P′。由已知截面β上的应变(εβ，γβ/2)，过莫尔应变圆上点C(εβ，γβ/2)作该平面法线的平行线交应变圆于一点P。

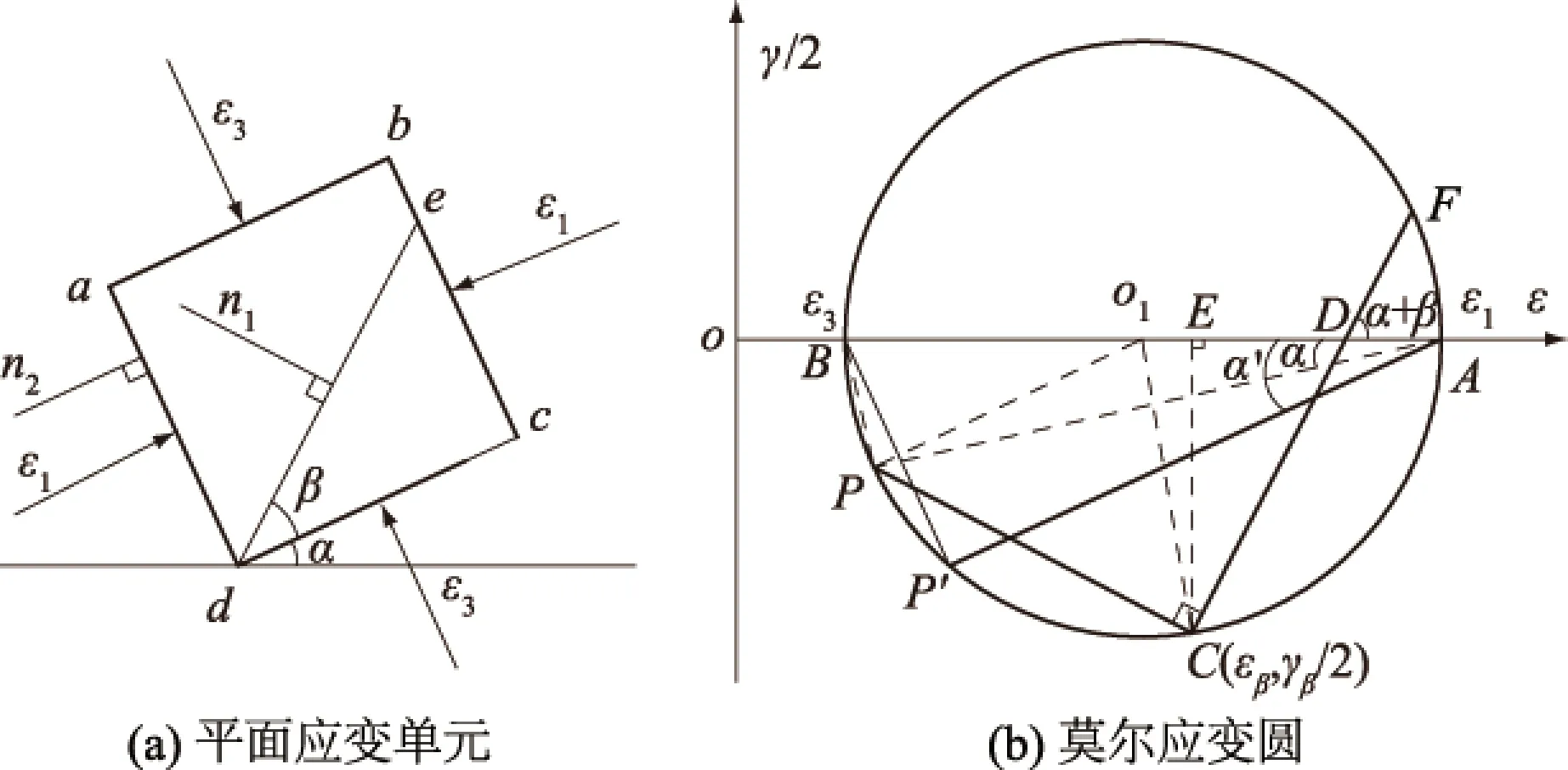
图3　法线法极点的唯一性证明Fig.3　Uniqueness proof of pole pointby normal line method

证明过程如下：

作辅助线连接PA，PB，CO1和PO1，作CE⊥AB于E。

(7)

直线O1E的长度为

(8)

因此，

在ΔCO1D中(图3(b))，∠O1CD=180°-∠CO1D-∠CDO1，即∠O1CD =β-α 。

由PC⊥CF，得∠PCO1=90°-∠O1CD，所以∠PCO1=90°- β+α 。

在ΔPO1C中，根据三角形的内角和为180°，∠PO1C=180°-2∠PCO1，即∠PO1C =2β-2α 。

在ΔPO1A中，∠PO1A=∠PO1C+∠CO1A=180° -2α。

所以∠BAP=∠BAP′=α。即证明AP与AP′重合，即点P与P′重合，即证得莫尔应变圆上利用平面法线法所作的极点具有唯一性。

4莫尔圆极点法的可靠性证明

利用极点法作图获得任意斜截面上作用的应变，是非常方便的，下面将证明极点法的可靠性，即通过极点法与通用的莫尔圆旋转法得到的结果进行比较，以验证极点法解决平面应变问题的准确性。

4.1平行线极点法的可靠性证明

已知单元体的平面应变状态(图4(a))，利用平行线法在其对应的莫尔应变圆上作出ae平面上的应变值点F′(εβ，γβ/2)(图4(b))。

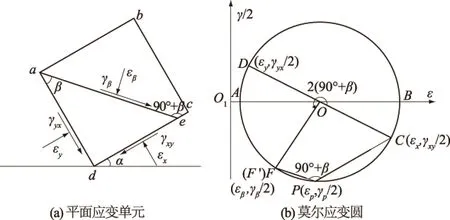
图4　平行线极点法的可靠性证明Fig.4　Reliability proof of determining pole pointby parallel line method

莫尔圆旋转法[8]步骤如下：由已知单元体的应变状态(图4(a))作出对应的莫尔应变圆(图4(b))。如图4(a)所示，ae平面可看作由cd平面逆时针转过90°+β得到。在莫尔应变圆上，ae平面上的应变值可由OC逆时针转过2(90°+β)得到，即C点绕圆心逆时针转过2(90°+β)得到点F(εβ，γβ/2)。

对比2种方法，发现∠CPF′为圆弧FDC的圆心角，∠COF为圆弧FDC所对应的圆周角，∠CPF′=2∠COF。显然，F点与F′点重合，所以极点法所求得的任意平面的应变值与莫尔圆作图法所得到的应变值相等，平行线极点法的解答与材料力学中的莫尔应变圆作图法求解所得的解是一致的。

4.2法线极点法的可靠性证明

已知单元体的平面应变状态(图5(a))。利用平行线法在其对应的莫尔应变圆上通过极点P作出ae平面上的应变值点F′(εβ，γβ/2)。

在图5(a)中，ae平面可视为由ac平面顺时针转过90°-β得到。在莫尔应变圆(图5(b))，ae平面上的应变值可由直线OC顺时针转过2(90°-β)得到，即点F的坐标(εβ，γβ/2)。

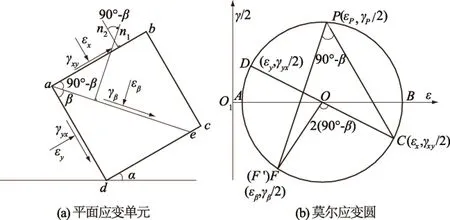
图5　法线极点法的可靠性证明Fig.5　Reliability proof of determining pole pointby normal line method

对比2种方法，发现∠CPF′为圆心角∠COF所对应的圆周角。显然，P点与P′点重合，所以极点法所求得的平面应变值与现有莫尔圆作图法所得到的值相等，即证明了莫尔应变圆法线极点法求解任意平面应变值的准确性。极点的定义方法虽然不同，但是对于求解相同问题的解答是相同的。

5极点法解决复杂问题的优越性

莫尔应变圆极点法对于解决复杂应变问题，具有独特的优越性。当只给定2个任意平面及所对应的应变值时，即2个任意平面不互相垂直(图6(a))，即θ≠90°，并且γA≠γB时，利用莫尔应变圆极点法可以容易确定该应变单元体上任一截面ef上的应变值。

在图6(a)中，按照通用莫尔圆旋转法可知，如果2个应变点的坐标值不在莫尔圆同一条直径上，则仅由这2点的坐标值无法确定唯一的莫尔圆。因此，复杂应变状态下，不能用通用莫尔圆旋转法确定微元体其他平面的应变状态。此时，建立ε-γ/2坐标系(图6(b))，由平行线极点法(或法线法)找到极点P，通过A，B，P三点即可作出莫尔应变圆。在莫尔圆上由极点作ef的平行线PC，与莫尔圆的交点C即为所求平面的应变值。

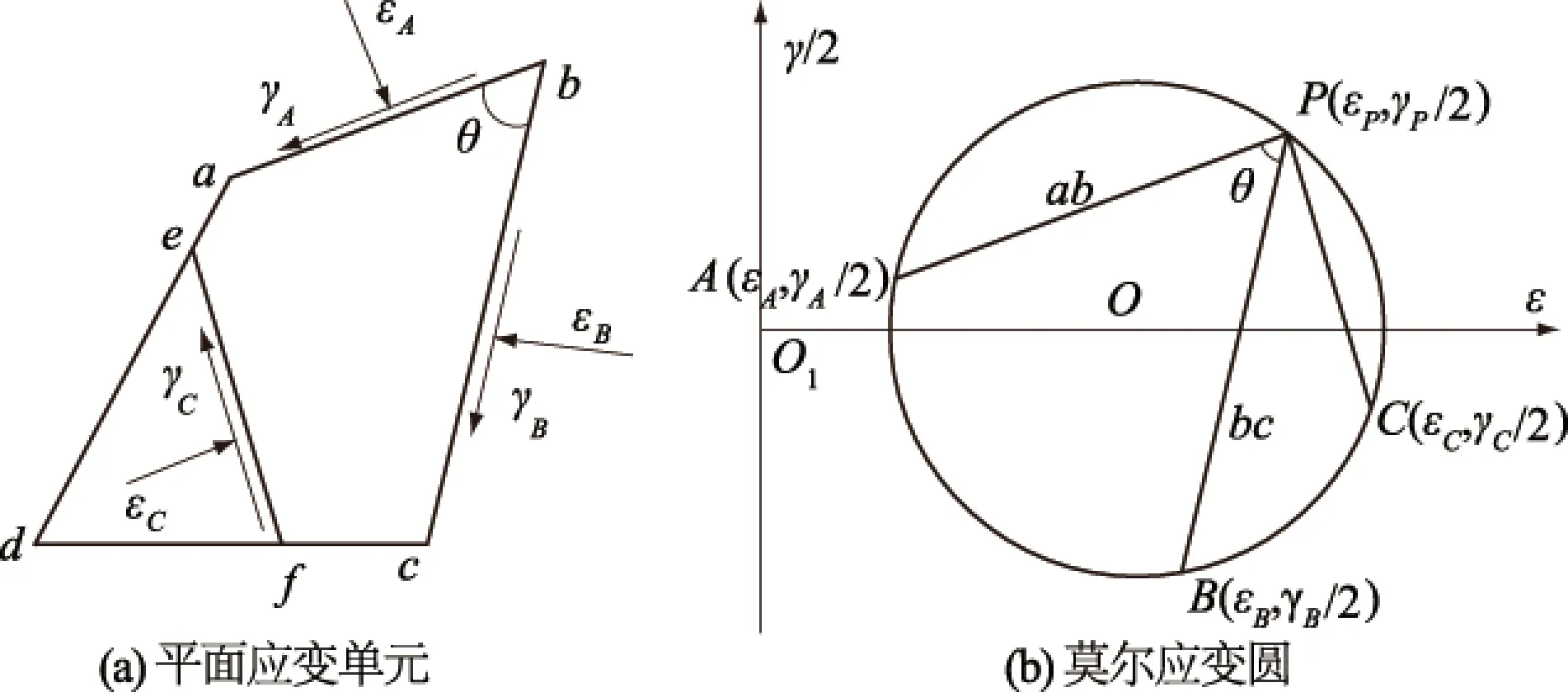
图6　任意平面应变单元与对应的莫尔应变圆Fig.6　Arbitrary plane strain element andcorresponding Mohrcircle of strain

由此可见，通过已知单元体任意夹角的平面应变状态求解任意截面上的应变值时，应用莫尔圆极点法求解具有简便、准确的优点。

6应变极点与应力极点的关系

根据应力-应变关系可知，对于给定的应力单元体(图7(a))，可以通过胡克定律确定其应变值。根据莫尔应力圆与应变圆关系[9]，当选定适当的比尺,即

(9)

式中:S1为应力比尺;S2为应变比尺；E为材料的弹性模量； μ为材料的泊松比。则应力圆与应变圆将有同一圆心，若一个圆的半径已知，可以在同一坐标系下将应力圆与应变圆作成同心圆(图7(b))。其中，两圆半径的关系为

(10)

式中：R为应力圆半径；r为应变圆半径。

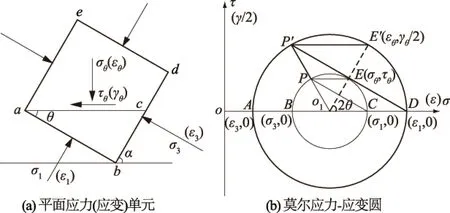
图7　应力极点与应变极点的位置关系Fig.7　Location relationship between stress pole pointand strain ploe point

在莫尔应力圆上，过点C作PC∥ab交圆与P点，则P点即为应力圆的极点，通过P点作ac面的平行线PE交应力圆于点E(σθ，τθ)。根据应力圆与应变圆的半径关系作出对应的莫尔应变圆。在莫尔应变圆上，得到应变极点P′，过P′点作ac面的平行线交圆于E′。则平面ac上的应变值为(εθ,γθ/2)。在图7(b)中，连接O1E′，O1E，根据通用莫尔圆旋转法可知∠EO1C=∠E′O1D=2θ。点O1，E和E′在同一条直线上。

在ΔPO1E中(图7(b))，∠PO1E=θ。由PE∥P′E′,得∠PEO1=∠P′E′O1=θ。

在ΔPO1E中∠PEO1=∠EPO1=θ，ΔP′O1E′中，∠PE′O1=∠EP′O1=θ，所以∠PO1E=∠P′O1E′。

根据几何关系，点O1，P和P′在同一条直线上。由此可知，当用在同一坐标系下，将莫尔应力圆与莫尔应变圆转化为同心圆时，应力极点与应变极点在同一条半径上。单元体的应力(应变)状态确定，对应的应变(应力)状态也就唯一确定。同时，应力(应变)极点也就唯一确定。

根据应力应变圆的关系，当已知单元体的应变状态(应力状态)及单元体的泊松比μ值时，通过应力极点与应变极点的关系及莫尔应力圆与应变圆的关系，可以快速地作出单元体的应变(应力)莫尔圆，并分析单元体任意方向面上的应变(应力)状态。

7结论

利用莫尔应变圆极点法可简便、准确地求解给定应变状态下，任意截面上的应变状态。同时在求解过程中可利用AutoCAD的绘图软件直接进行复杂应变问题的极点法求解。避免使用复杂的公式计算以及角度的正负方向判定，是一种极为简便、有效的求解应变问题的方法。通过对莫尔应变圆极点法及应力应变极点关系的研究，得到以下结论：

(1) 莫尔应变圆的极点有2种定义方法，一是平行线法，即通过已知平面的应变值在圆上对应点，作已知应变平面的平行线交于圆的另一点。通过该点作未知平面的平行线与莫尔圆的交点，即为未知平面的应变值。二是法线法，即过已知平面的应变值在莫尔圆上的对应点，作已知应变平面法线的平行线交于圆的另一点。通过该点作未知平面法线的平行线与莫尔圆的交点，即为未知平面的应变值。

(2) 2种方法定义的极点方法不同，定义的极点在莫尔圆上位于同一条直径上，但是对于平面应变问题的解答是相同的。

(3) 利用莫尔应变圆极点法求解时，给定平面的应变状态，作极点的方法选定，则该莫尔应变圆上有且只有一个极点。

(4) 莫尔圆极点法在求解应变问题时具有简便、准确的优点，特别适用于复杂应变情况。

(5) 对于给定单元体的应变(应力)状态，通过一定的比例关系，莫尔应变圆与应力圆可以在同一坐标系下用同心圆表示。应变极点与应变极点一一对应，两者在同一条半径上。在莫尔圆上，通过作与已知应变平面的任意夹角平面的平行线是否存在应变极点的问题还需进一步探索。另外，对于应变圆极点法在岩土工程应用还需要进一步的研究。

参考文献：

[1]TIMOSHENKOS.HistoryofStrengthofMaterials[M].NewYork:DoverPublicationsInc., 1983.

[2]ALLISONI.ThePoleoftheMohrDiagram[J].JournalofStructuralGeology, 1984, 6(3): 331-333.

[3]TERZAGHIK.TheoreticalSoilMechanics[M].NewYork:JohnWielyandSons, 1943: 15-65.

[4]LAMBET,WHITMANR.SoilMechanics[M].NewYork:JohnWielyandSons, 1969.

[5]BUDHUM.SoilMechanicsandFoundations(ThirdEdition)[M].NewYork:JohnWielyandSons,2011:131-185.

[6]DASBM.PrinciplesofGeotechnicalEngineering(SeventhEdtion)[M].India:CLEngineering, 2010.

[7]HOLTZR,KOVACSW.AnIntroductiontoGeotechnicalEngineering[M].NewJersy:PrenticeHall, 1981.

[8]GEREJM,GOODNOBJ.MechanicsofMaterials[M].Canada:RPKEditorialServicesInc., 2009:536-616.

[9]HEARNEJ.MechanicsofMaterials(ThirdEdition)[M].UK:Butterworth-Heinemann, 1997: 220-290.

[10]HIBBELERRC.MechanicsofMaterials[M].NewJersy:PrenticeHall, 2010.

[11]李大勇,郭彦雪,高玉峰. 莫尔圆极点法原理及应用[J].岩土工程学报,2013,35(10)：1883-1888.

[12]李大勇,翟汉波,高玉峰.莫尔圆极点确定的新方法[J].岩土力学,2015,36(6):1622-1626.

(编辑：刘运飞)

Study on the Pole Point Method of Mohr Strain Circleand the Characteristics of Strain Pole Point

ZHAIHan-bo1,2,LIDa-yong1,2,LIUQing-song2,WANGKai-ting2

(1.KeyLaboratoryofCivilEngineeringDisasterPreventionandMitigation,ShandongUniversityofScienceandTechnology,Qingdao266590,China; 2.CollegeofCivilEngineeringandArchitecture,ShandongUniversityofScienceandTechnology,Qingdao266590,China)

Abstract:The pole point on Mohr circle of strain is a point so special that it can help to readily find strains on any specified plane by using diagram instead of complicated computation. In this paper, two methods are put forward to determine the pole point on the Mohr circle of strain, i.e. the parallel line method and the normal line method. On the basis of contradiction method, the uniqueness of strain pole point is proved by parallel line method and normal line method; on the basis of geometric graphical method, the reliability of determining strain pole point by parallel line method and normal line method is verified. Research shows that the two strain pole points determined by the two methods are on a diameter line of the Mohr strain circle. When certain proportional relation is given, the corresponding stress pole point and the strain pole point are on the radius line of the concentric circle consisting of the Mohr stress circle and Mohr strain circle. The strain pole point method is a preferred solution to determine complex strain state of the strain element and the deformations in geotechnical fields.

Key words:Mohr circle; pole point; stress; strain; uniqueness; rotation method

收稿日期：2015-07-05；修回日期：2015-08-01

基金项目：国家自然科学基金项目(51379118)；山东省土木工程防灾减灾重点实验室开放课题基金项目(CDPM2013KF02)；山东科技大学研究生科技创新基金项目(YC150327)

作者简介：翟汉波(1989-)，男，山东泰安人，硕士研究生，主要从事海洋岩土工程研究，(电话)15621459517 (电子信箱)zhaihanbo@qq.com。

doi:10.11988/ckyyb.20150561

中图分类号：TU47

文献标志码：A

文章编号：1001-5485(2016)06-0088-06

2016,33(06):88-93