基于区域的活动轮廓图像分割模型的变步长优化算法

郑汉翔，王美清

(福州大学数学与计算机科学学院，福建 福州　350116)

基于区域的活动轮廓图像分割模型的变步长优化算法

郑汉翔，王美清

(福州大学数学与计算机科学学院，福建 福州350116)

摘要：基于偏微分方程图像分割的活动轮廓模型，基本思想是将图像分割归结为最小化一个封闭曲线的能量泛函, 图像分割问题实质上是一个无约束最优化问题. 传统最小化算法的数值实现过程中采用固定时间步长的方法, 时间步长选取较大，迭代过程容易出现震荡现象影响分割结果，而时间步长选取较小，又会减慢收敛速度. 利用Wolfe-Powell线搜索方法，提出了一种变时间步长的优化算法，在迭代过程中根据搜索方向自动调整时间步长大小，有效克服了固定时间步长出现的震荡现象和收敛速度慢的问题.

关键词：图像分割； 非精确线搜索； 活动轮廓； 时间步长

0引言

图像分割是图像处理和计算机视觉的基本问题之一，其目的是把感兴趣的对象从给定图像中分离出来. 基于活动轮廓模型图像分割是当前的一个热门研究课题，特别是基于区域的活动轮廓模型，由于它的鲁棒性以及能很好地结合图像信息而被广泛应用. 活动轮廓模型(或Snake模型)是由Kass等[1]首先提出的，其基本思想是将图像分割问题归结为最小化一个封闭曲线的能量泛函[2]. Chan等[3]提出的CV模型是应用最广泛的一种基于区域的图像分割模型，该模型利用活动轮廓内部和外部的灰度均值近似分割图像，对同质图像可以得到很好的分割结果. Li等[4]提出了LBF模型克服了CV模型不能处理非同质图像的缺点，该模型利用图像的局部信息控制轮廓曲线演化，能有效地克服灰度不均现象.

梯度下降法是求解活动轮廓模型能量最小化问题最简单直接的算法，图像处理中的传统方案是通过计算负梯度方向作为能量下降方向，并且以固定的时间步长迭代求解. 但是在迭代过程中，如果时间步长选取过小，将会影响收敛速度； 如果时间步长选取过大，求解过程会出现震荡现象影响分割结果. 因此，近年来许多学者针对活动轮廓图像分割模型提出了新的求解算法. 如Goldstein等[5]采用了分裂Bregman迭代算法求解凸化的CV模型，另外还有Newton 方法和Quai-Newton法[6]等. Bregman迭代出自泛函分析的概念，该算法要求所求模型必须为凸模型； 在数值优化中，Newton法比梯度下降法拥有更快的收敛速度，但Newton法计算与存储Hessian矩阵的开销很大，并且当Hessian矩阵奇异时牛顿方向不存在或者不是函数的下降方向； Quai-Newton法虽然不需要计算Hessian，但是Quai-Newton法在储存矩阵以及通过求解线性方程组来计算搜索方向上，在图像处理中开销依然很大.

针对传统活动轮廓迭代格式中选取固定时间步长的问题，应用Wolfe-Powell非精确线搜索准则提出一种变步长算法. 在迭代求解过程中，根据求得的下降方向自动调节时间步长，提高收敛速度的同时克服了震荡现象. 实验结果验证了该方法的有效性.

1基于区域活动轮廓分割模型

1.1CV模型

CV模型[3]假设分割图像I为分片常数图像，通过最小化如下由水平集表示的能量泛函来实现分割：

(1)

其中： λ1，λ2，μ∈R+； Ω⊂R2表示图像区域； φ(x):Ω→R表示水平集函数； c1和c2分别表示演化曲线内部和外部的灰度平均值.

(2)

式中:H(·)和δ(·)分别表示Heaviside函数和Dirac函数，参考文献[3]，取正则化的Heaviside函数Hε(·)和δε(·)：

CV模型利用图像全局信息，因此对初始曲线不敏感且对噪声具有鲁棒性. 但由于假设待分割图像为分片常数图像，因此无法处理灰度分布不均的非同质图像.

1.2LBF模型

为了分割非同质图像，LBF模型[4]通过引入核函数定义了一个局部二值拟合水平集能量泛函：

(3)

其中： η1，η2，ν，μ∈R+； H(·)和δ(·)分别表示Heaviside函数和Dirac函数； Kσ为高斯核函数； f1(x)和f2(x)为图像在x点的局部拟合值.

(4)

LBF模型的后两项为长度项和避免重新初始化的正则化项.

在LBF模型中,f1(x)和f2(x)利用了图像的局部信息，因此能够很好地处理灰度分布不均的非同质图像. 但是由于未涉及全局信息，该模型对初始轮廓和噪声没有鲁棒性. 实验结果还表明, LBF模型对时间步长极其敏感.

1.3传统求解方案

对CV模型(1)和LBF模型(3)分别用变分法获得梯度公式：

(5)

(6)

再利用下列迭代格式更新水平集函数：

(7)

在最小化活动轮廓模型的迭代过程中，由式(5)和(2)交替更新φ和c1、c2来求解CV模型，由式(6)和(4)交替更新φ和f1、f2来求解LBF模型. 数值实现过程中涉及时间步长Δt的选取，传统的求解方法一般通过多次实验选取固定的时间步长Δt. 为了避免分割结果产生震荡现象，往往取Δt为一较小的值，因此传统方法收敛速度比较慢.

2变步长优化算法

2.1Wolfe-Powell线搜索

在上述的求解过程中，只能通过多次实验手动选取时间步长，并且在迭代过程中时间步长是固定的，不会根据搜索方向的变化而变化. 实验结果表明过大的时间步长会产生震荡现象影响分割结果，因此为了保证分割结果，往往只能选择较小的时间步长，但这将会增加迭代次数影响收敛速度.

(8)

(9)

由于准则(8)和(9)有可能把步长因子的极小值排除在可接受区间之外，后来Wolfe、 Powell等又给出了更为简单的条件代替(9)式，详见：

(10)

其中：c2∈(c1，1). 有时也用另一种条件更强的不等式：

(11)

来代替不等式(10). 联合式(8)和(10)或式(8)和(11)即是著名的Wolfe-Powell准则[7-8].

由于Armijo-Goldstein准则和Wolfe-Powell准则均具有良好的收敛性质和不错的数值表现，至今仍在许多数值计算和工程中广泛采用[9].

利用Wolfe-Powell准则确定式(7)中的时间步长Δt，具体算法如下：

算法1Wolfe-Powell线搜索算法

Step1: 给定xk，设c1=0.000 1，c2=0.9，β=0.8，Δt=1;

Step2: 根据公式(5)或者(6)计算能量泛函的梯度▽φF(xk)，并且设搜索方向为负梯度方向d=-▽φF(φk)，若F(xk+Δtd)≤F(xk)+c1Δt▽φF(xk)Td，转入Step3，否则转入Step4；

Step3:Δt=Δt/β，若F(xk+Δtd)>F(xk)+c1Δt▽φF(xk)Td，停止； 否则转入Step2；

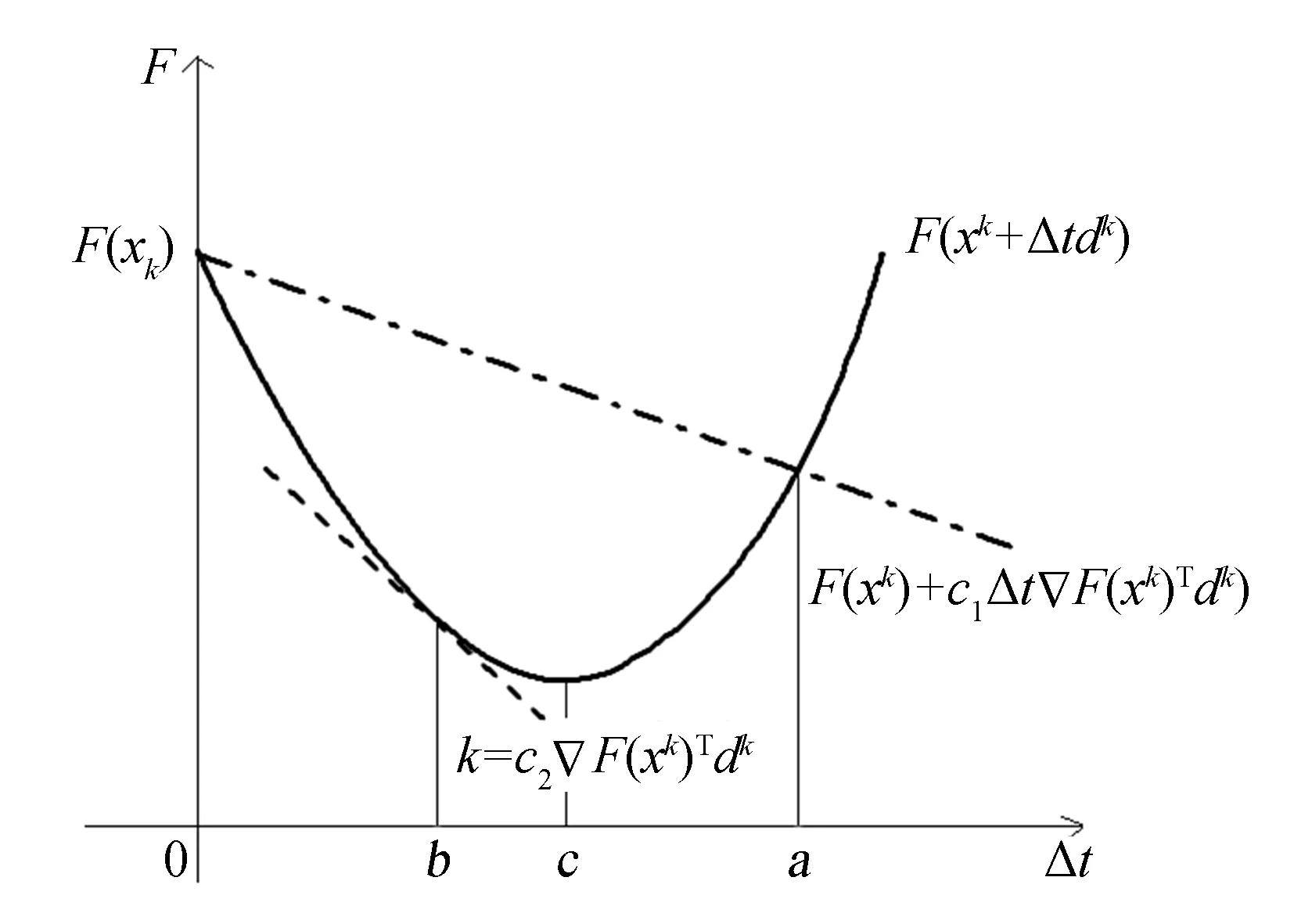
Step4:Δt=Δt·β，若▽φF(xk+Δtd)Td

2.2变步长优化算法

利用Wolfe-Powell线搜索算法，提出了能量最小化问题的变步长优化算法. 首先根据式(5)或(6)确定能量泛函的负梯度方向为搜索方向dk=-▽φF(φk)，然后由算法1确定时间步长Δt； 将dk和Δt代入公式(7)更新水平集函数φk. 重复使用上述过程直至相邻两次水平集函数满足停止标准. 用相邻两次迭代产生的水平集函数的近似程度作为停止标准.

具体算法如下：

算法2变步长优化算法

Step1: 给定初始轮廓曲线φ0，给定迭代停止标准δ；

Step2: 计算搜索方向dk=-▽φF(φk)；

Step3: 由算法1确定时间步长Δt，利用式(7)更新φk；

该算法跟踪曲线演化过程中的梯度方向，动态地调节时间步长，有效避免了手动选取步长导致的震荡现象和收敛速度慢的问题.

2.3方法可行性分析

图1　时间步长选取示意图Fig.1　Diagram for the choosing of time step

将F定义为以Δt为自变量的函数，xk，dk均为常量. 则图1中实线表示函数F(xk+Δtdk)，点划线表示函数F(xk)+c1Δt▽F(xk)Tdk，虚线表示斜率为c2▽F(xk)Tdk且与函数F(xk+Δtdk)相切的直线.Wolfe-Powell准则(8)式保证Δtb，所以算法选取的时间步长Δt的可接受区间被限制在[b，a]，其中包括极小值点c. 因此经过迭代可以收敛到极小值点. 而传统方法选取固定的时间步长，如果选取过大的时间步长，函数F(xk+Δtdk)将越过极小值点，并且在极小值点附近徘徊，这将造成震荡现象而无法收敛，所以必须选取较小的时间步长才能保证函数充分接近极小值点，这样又导致收敛速度缓慢.

在算法实现过程中，将Wolfe-Powell线搜索的最大循环次数限制为常数40，因此变步长算法的时间复杂度为T(N)=O(N)+O(c·N)=O(N)，与传统的梯度下降法一致. 但是传统算法迭代过程选取的时间步长近似于可接受区间里的最小值，因此每次分割都接近算法的最坏情况，而变步长算法选取可接受区间内的最大步长，避免了最坏情况的发生.

3实验结果

3.1CV模型

图2、 3均为对CV模型分别应用传统求解方法和变步长算法获得的实验结果. 图2(a)、 3(a)是原始图像和初始轮廓线; 图2(b)、 3(b)为传统方法求解结果，迭代次数分别为132次和142次，迭代时间分别为1.41 s和2.06 s； 图2(c)、 3(c)是采用变步长方法求解结果，迭代过程自动选取时间步长，迭代次数分别为71次和68次，迭代时间分别为0.98 s和1.47 s. 从实验结果可以看出，变步长方法在保证分割结果的同时减少迭代次数，加快了迭代收敛速度. CV模型对时间步长大小相对不敏感，所以变步长方法在CV模型中主要起自动选取时间步长以及加速收敛的作用.

图2　同质图像的CV模型分割结果Fig.2　Segmentation result of CV model for homogeneous image

图3　带噪声几何图形的CV模型分割结果Fig.3　　　　Segmentation result of CV model for geometric 　　　figure with noise

3.2LBF模型

图4是对LBF模型分别用传统迭代方法和变步长方法的分割结果. 图4(a)～(c)是利用传统迭代方法求解LBF模型在不同时间步长下的分割结果. 可以看出在传统迭代方法中，时间步长的微小变化会严重影响LBF模型的分割结果和迭代次数，即LBF模型是对时间步长较为敏感的一种模型. 图4(d)为变步长方法的迭代结果，变(时间)步长方法避免了LBF模型对时间步长的敏感性.

图4　LBF模型的分割结果Fig.4　Segmentation result of LBF model

图5　LBF模型能量变化曲线　　　Fig.5 Energy curve of LBF model

图5是LBF模型的能量变化曲线，横坐标表示迭代次数，纵坐标表示函数能量. 其中红色实线为变步长方法的能量下降曲线，蓝色点线、 黑色点划线、 绿色虚线代表用传统迭代方法分别取Δt=0.15、 0.20、 0.25时的能量下降曲线.

当时间步长为0.20时，能量泛函最小化过程出现震荡现象，从图4(b)中可以看出分割结果受到影响，同时震荡现象使得停止标准失效，而当时间步长大于0.20时，能量泛函没有收敛到最小，对应图4(c)则无法分割. 通过反复实验发现传统方法选取时间步长为0.15时达到最佳的分割结果，迭代次数为275次，用时3.38 s (见图4(a)). 而采用变步长方法自动选取时间步长，得到最佳分割结果的同时，加快收敛速度，迭代次数仅为109次，用时2.26s (见图4(d)).

4结论

在传统活动轮廓模型数值最优化算法的基础上，提出一种变时间步长算法. 该算法根据每次迭代求得的搜索方向自动调节时间步长. 实验结果表明，该方法克服了传统方法选取较大时间步长时出现的震荡现象，同时减少了迭代次数，加速了算法收敛.

参考文献：

[1] KASS M，WITKIN A，TERZOPOULOS D. Snakes: active contour models[J]. International Journal of Computer Vision，1988，1(4): 321-331.

[2] MUMFORD D，SHAH J. Optimal approximation by piece-wise smooths functions and associated variational problems[J]. Communications on Pure and Applied Mathematics，1989，42(5): 677- 685.

[3] CHAN T F，VESE L A. Active contours without edges[J]. Image Processing，IEEE Transactions on，2001，10(2): 266-277.

[4] LI C，KAO C Y，GORE J C，etal. Implicit active contours driven by local binary fitting energy[C]//Computer Vision and Pattern Recognition. Minneapolis: IEEE Conference Publications，2007: 1-7.

[5] GOLDSTEIN T，BRESSON X，OSHER S. Geometric applications of the split Bregman method: segmentation and surface reconstruction[J]. Journal of Scientific Computing，2010，45(1/2/3): 272-293

[6] CHAN T F，ESEDOGLU S，NIKOLOVA M. Algorithms for finding global minimizers of image segmentation and denoising models[J]. SIAM Journal on Applied Mathematics，2006，66(5): 1 632-1 648.

[7] BOYD S P，VANDENBERGHE L. Convex optimization[M]. Cambridge: Cambridge University Press，2004.

[8] 黄红选，韩继业. 数学规划[M]. 北京： 清华大学出版社，2006.

[9] 朱训芝，唐焕文. 一种新的无约束优化线搜索算法[J]. 运筹与管理，2005，14(5): 18-23.

(责任编辑： 洪江星)

A variable step-size optimization algorithm based on active contour model

ZHENG Hanxiang，WANG Meiqing

(College of Mathematics and Computer Science，Fuzhou University，Fuzhou，Fujian 350116，China)

Abstract:The basic idea of PDE-based image segmentation based on the active contour model is to minimize the energy functional on a closed curve. Thus, the image segmentation problem is in essence an unconstrained optimization problem. The traditional minimization uses, a fix time step which may produce some problems. The large time step may lead to the oscillation of energy functional, while the small time step will slow down the convergence speed. A variable step-size method is proposed by using the Wolfe-Powell line search method. Our method will adjust time step at each iteration according to the search direction which effectively overcome the oscillation of energy functional and the defect on convergence speed.

Keywords:image segmentation; inexact line search; active contour; time step

DOI:10.7631/issn.1000-2243.2016.03.0419

文章编号：1000-2243(2016)03-0419-05

收稿日期:2014-01-17

通讯作者:王美清(1967-), 教授，主要从事图像处理技术、 视频压缩算法、 数值算法方面研究，mqwang@fzu.edu.cn

基金项目:国家自然科学基金资助项目(11071270)

中图分类号：TP391

文献标识码：A